Implementarea automatelor combinationale cu ajutorul multiplexoarelor

Obiectivele lucrarii

Dupa aceasta lucrare de laborator studentii vor fi capabili sa

aplice teorema de expansiune a lui Shannon pentru implementarea functiilor logice cu ajutorul multiplexoarelor (MUX),

recunoasca tipurile de implementari cu multiplexoare (tipurile 0,1,2 si 3),

obtina implementari echivalente de tipuri diferite pentru aceeasi functie logica,

aplice metode speciale pentru proiectarea cu multiplexoare,

simuleze functionarea automatelor cu mupltiplexoare CircuitMaker.

Exemplul 1

In general, atunci cand se doreste implementarea unei functii logic ecu ajutorul multiplexoarelor, nu este necesar ca functia respectiva sa fie minimizata in maniera obisnuita. Pentru a ilustra procedura de implementare vom incepe prin luarea in considerare a functiei

,

care va fi implementata sub forma unui automat cu multiplexor de tip 0. O implementare pentru tipul 0 se obtine folosind fie forma compacta a mintermenilor unei functii booleene, fie reprezentarea sub forma unui tabel de adevar. O implementare de tipul 0 nu necesita partitionarea nici unui semnal in tabelul de adevar. O implementare de tipul 1 presupune partitionarea unui singur semnal. O implementare de ordinul 2 presupune partitionarea a doua semnale. Semnalele independente vor fi aplicate la intrarile de selectie ale MUX

Pentru functia data,

si

, asa incat implementarea de tip 0 (nici o variabila la intrarile de date ale MUX) se obtine conectand intrarile de date la 0 sau 1, ca in Figura 3.1.

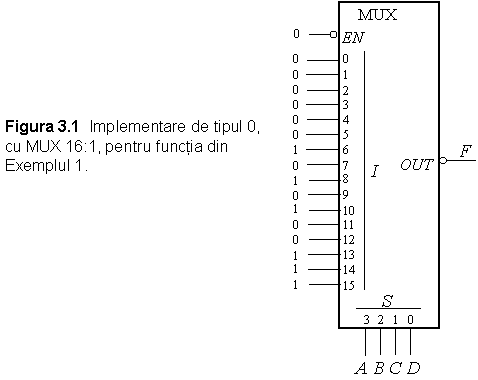
Se observa in Figura 3.1 ca o intrare de date se conecteaza la valoarea logica a mintermenului cu acelasi numar. De exemplu, intrarea de date 7 se conecteaza la 1, iar , s.a.m.d. In implementarea prezentata a fost inclus un inversor pentru ca iesirea activa 0 conduce la expresia si noi avem nevoie de .

O implementare de tipul 1 se obtine aplicand teorema de expansiune a lui Shannon.

si

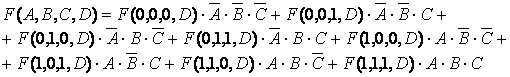
Dar

,, ,

,, ,

asa incat implementarea de tipul 1 (o variabila la intrarile de date) se obtine conectand intrarile de date la valorile functiei care multiplica mintermenii corespunzatori. De exemplu, intrarea de date 5 se conecteaza la valoarea care multiplica mintermenul 5 () adica la , s.a.m.d.

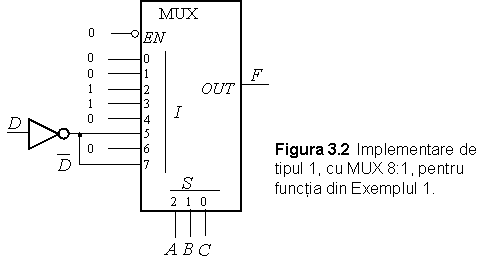
In consecinta, implementarea de tipul 1 este prezentata in Figura 3.2. La intrarile de selectie sunt variabilele independente , , .

O implementare de tipul 2 va avea doua variabile independente la intrarile de selectie si doua variabile, eventual pre-procesate, la intrarile de date. De aceasta data, vom avea nevoie de un MUX 4:1.

Aplicam din nou teorema de expansiune a lui Shannon sub forma:

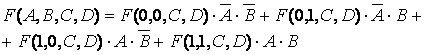
iar

, , , .

Din nou, intrarile de date se conecteaza la valorile functiei care multiplica mintermenii corespunzatori. De exemplu, intrarea de date 3 se conecteaza la valoarea care multiplica mintermenul 3 () adica la , s.a.m.d. Implementarea este cea prezentata in Figura 3.3.

In sfarsit, o implementare de tipul 3 va avea o singura variabila independenta la intrarea de selectie si trei variabile, eventual pre-procesate, la intrarile de date. De aceasta data, vom avea nevoie de un MUX 2:1.

Aplicam si de aceasta data teoreme de expansiune a lui Shannon sub forma:

si

, .

Implementarea este prezentata in Figura 3.4.

Exemplul 2

Pentru functia din Exemplul 1, implementarile de tipul 1, 2 si 3 pot fi obtinute si in alt mod. Se foloseste tabelul de adevar al functiei date, partitionat in functie de una (tipul 1), doua (tipul 2) sau trei variabile (tipul 3), ca in Figura 3.5. Desigur, implementarile vor fi aceleasi ce cele de mai sus, pentru ca s-au ales aceleasi variabile independente cu aceleasi ponderi.

Desfasurarea lucrarii

Parcurgeti toate etapele prezentate la Exemplul 1 si la Exemplul 2. In final, trebuie sa obtineti schemele automatelor implementate cu MUX in CircuitMaker, sa simulati functionarea lor si sa prezentati rezultatele simularii in referatul de laborator.

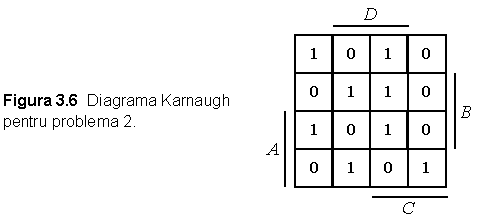
Gasiti o implementare pentru functia logica a carei diagrama Karnaugh este prezentata in Figura 3.6:

a)      folosind numai porti logice NAND,

b)      cu MUX, de tipul 1,

c)      cu MUX, de tipul2.

Simulati functionarea in fiecare caz si prezentati rezultatele in referatul de laborator.

Figura 3.6 Diagrama Karnaugh pentru problema 2.

Se considera functia

Determinati:

a)      o implementare cu un MUX 8:1

b)      o implementare cu doua MUX 4:1 si un MUX 2:1

Indicatie pentru b: Tabelul de adevar al functiei se imparte in doua. Fiecare parte se implementeaza cu cate un MUX 4:1 cu variabilele de selectie , (de exemplu). Apoi, iesirile celor doua multiplexoare vor fi conectate la intrarile unui MUX 2:1.

Simulati functionarea in fiecare caz si prezentati rezultatele in referatul de laborator.