Lucrul cu matrice

1 Masive

Numeroase probleme economice utilizeaza reprezentari de date omogene carora le corespund masive unidimensionale, bidimensionale si multidimensionale. Un loc special il ocupa calculul matriceal. Problemele de bilant contabil se rezolva cu ajutorul matricelor. Problemele balantei legaturilor dintre ramuri utilizeaza reprezentarea matriceala. De asemenea, in domeniul cercetarilor operationale matricea tehnologica. Rezolvarea algoritmului simplex presupune lucrul dupa regula dreptunghiului. In econometrie, metoda celor mai mici patrate in mai multe trepte foloseste expresii de calcul matriceal.

Acest capitol abordeaza o serie de aspecte legate de construirea unei clase matrice ce contine proceduri utilizate pentru solutionarea de probleme in care apar ca operanzi matricele.

Structurile de date de tip masiv reprezinta instrumente de stocare a datelor sub forma de zone compacte si continue din memoria calculatorului. Indiferent de tipul sau, fie ca este unidimensional, bidimensional sau multidimensional, structura de date de tip masiv este reprezentata in memorie de un sir continuu de zone de memorie de dimensiune egala cu marimea in octeti a tipului de data asociat unui element al masivului. Deoarece elementele unui masiv sunt omogene din punct de vedere al tipului lor dimensiunea in octeti a unui masiv este determinata prin relatia:

Dim = nr_elem * dim_elem

unde:

Dim - dimensiunea in octeti a masivului;

nr_elem - numarul de elemente din masiv;

dim_elem - dimensiunea in octeti a uni element.

Diferenta dintre tipurile de masive este logica si se concretizeaza in modul de repezentare a unui masiv, precum si in modul de accesare a elementelor sale.

Figura 1 descrie tipul de masiv unidimensional, in care v[i] reprezinta elementul al i-lea din masiv, iar v este numele masivului si pointer la adresa de inceput a acestuia.

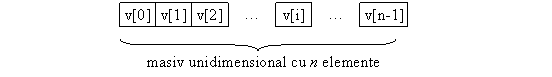
Fig. 1. Masiv unidimensional.

Figura 2 descrie tipul de masiv bidimensional, in care a[i][j] reprezinta elementul de pe linia i si coloana j din matricea a. De asemenea, variabila a reprezinta pointer la adresa de inceput a zonei de memorie rezervata matricei.

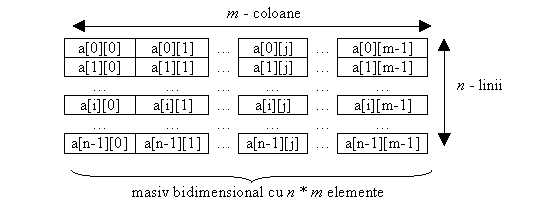
Fig. Masiv bidimensional.

Figura 3 descrie tipul de masiv tridimensional, in care c[k][i][j] reprezinta elementul de pe linia i si coloana j din tabloul k al masivului tridimensional c.

Fig. 3. Masiv tridimensional.

Clasa matrice implementeaza modul dinamic de lucru cu matrice. Clasa contine un pointer la masiv bidimensionale, a, ce contine elemente de tip int si dimensiunile acestuia, numarul de linii, n, respectiv, numarul de coloane, m.

class matrice

Masivul bidimensional este declarat prin variabila de tip pointer a. Aceasta este accesata numai in interiorul clasei deoarece are dreptul de acces implicit private. Numarul de linii este reprezentat variabila n, iar numarul de coloane de variabila m.

Daca in varianta dinamica restrictiile de dimensiune sunt date de capacitatea memoriei si de eperienta utilizatorului, in varianta statica dimensiunile masivelor sunt limitate suprior de valori intregi constante.

In varianta statica masivele sunt definite astfel :

masivul unidimensional v cu maxim 100 de elemente:

int v[100];

masivul bidimensional a cu maxim 30 de linii si 30 de coloane:

int a[30][30];

masivul tridimensional c cu maxim 30 de tablouri de dimensiune maxima 20 linii si 20 coloane:

int c[30][20][20];

In varianta dinamica definirea este realizata in urmatorul mod:

pointer la masivul unidimensional v:

int *v;

pointer la masivul bidimensional a:

int **a;

pointer la masivul tridimensional c:

int ***c;

Alocarea zonei de memorie aferenta masivelor se realizeaza prin implementarea functiei void * malloc (size_t):

masivul unidimensional v cu n elemente de tip int:

int *v = (int *)malloc(n * sizeof(int));

masivul bidimensional a cu n linii si m coloane ce contine elemente de tip int:

int **a = (int **)malloc(n * sizeof(int *));

for (int i=0;i<n;i++) a[i]=(int*)malloc(m * sizeof(int));

masivul tridimensional c cu o tablouri de dimensiune n X m cu elemente de tip int:

int ***c = (int ***) malloc (o * sizeof(int **));

for(int k=0;k<o;k++)

In ceea ce priveste implementarea functiilor de prelucrare abordarea dinamica a masivelor nu implica secvente de cod diferite care sa prelucreze elementele unui masiv alocat dinamic sau static.

Functii de intrare si iesire

Pentru realizarea calculului matriceal este necesara existenta matricei sau a matricelor. Crearea necorespunzatoare a obiectului de lucru, si anume matricea, duce la efecte total neasteptate. De aceea, pentru a fi lipsiti de neplaceri, atentia acordata acestor functii este maxima.

In calculul matriceal sunt incluse si functii de intrare si iesire. Aceste functii realizeaza:

crearea matricei, fie de la consola, fie initializata implicit cu valoarea zero;

afisarea matricei pe ecran.

In continuare se prezinta functiile care realizeaza creare matricei. In practica se observa, ca pe langa matricea dorita, sunt folosite o serie de matrice ajutatoare cum ar fi matricea unitate, matricea booleana, matricea cu 1 pe o linie si in rest zero etc.

Clasa matrice are definiti doi constructori. Unul este implicit fara parametri si realizeaza introducerea matricei de la tastatura, iar cel de-al doilea primeste ca parametrii numarul de linii si de coloane si creaza matricea cu elementele zero.

Constructorul implicit este:

matrice::matrice()

Alocarea dinamica presupune utilizarea memoriei intr-un mult mai eficient si anume se aloca memorie exact cat este necesar pentru memorarea matricei. Pentru a realiza aceasta se foloseste functia membru int** aloc_mat(int, int). Dupa cum se observa din secventa prezentata mai sus alocarea memoriei necesare matricei se realizeaza dupa introducerea numarului de linii si coloane. Este foarte important sa nu se omita acest pas, altfel rezultatele obtinute fiind cu totul altele. Functia de alocarea a matricei are ca drept de acces private.

int ** matrice::aloc_mat(int n,int m)

Functia primeste ca date de intrare numarul de linii n si numarul de coloane m al matricei si intoarce un pointer la aceasta. La inceput este alocata zona de memorie pentru un vector de pointeri, ce reprezinta inceputul fiecarei linii a matricei. Vectorul contine n componente. Urmeaza alocarea zonei de memorie pentru fiecare linie a matricei. Linia matricei este alcatuita din m elemente. Dupa alocarea spatiului necesar memorarii matricei se continua cu introducerea elementelor matricei.

Constructorul cu parametrii initializeaza toate elementele matricei cu valoarea zero:

matrice::matrice(int k,int l)

Implementa unor functii care creaza matrice speciale, matricea unitate, matricea cu o linie/coloana cu elemente ce au valoarea unu necesare in rezolvarea de probleme economice implica prelucrarea elementelor matricei create prin utilizarea constructorului cu paametrii.

De exemplu in clasa matrice matricea booleana este obtinuta cu ajutorul functiei membre fara tip creare_bool_matrice(matrice &). Functia primeste ca parametru de iesire un obiect de tip matrice care se transfera prin referinta. Parametrul de intrare este reprezentat de pionterul this caruia i se asociaza obiectul de tip matrice , matrice booleana. Functia este urmatoarea :

void matrice::creare_bool_matrice(matrice &b)

Dupa efectuarea operatiilor este foarte important sa vizualizam efectele create. Acesta se realizeaza cu ajutorul functiilor de iesire.

Functia void afisare_matrice() afiseaza pe ecran matricea x. Ea are ca parametrii de intrare pointerul implicit this :

void matrice::afisare_matrice()

}

else cout<<'nMatrice vida !!!';

3 Proceduri de calcul

Aceasta categorie de proceduri se refera la operatiile cu matrice. Aceasta categorie include adunarea a doua matrice, inmultirea a doua matrice, transpunerea unei matrice, diferenta dintre doua matrice, inversa unei matrice ridicarea la putere a unei matrice etc.

In clasa matrice operatia de inmultire este realizata prin supraancarcarea operatorului "*". Functia de supraincarcare este urmatoarea:

matrice matrice::operator*(matrice b)

}

return c;

Procedura de supraincarcare intoarce un obiect de tip matrice si anume rezultatul inmultirii celor doua matrice, care este creat in interiorul procedurii( obiectul c). Procedura primeste ca parametru de intrare un obiect de tip matrice si anume obiectul b. Acesta reprezinta operandul din partea dreapta a inmultirii. Operandul stang al inmultirii este dat de pionterul this. Inmultirea a doua matrice se realizeaza doar daca numarul de coloane a primei matrice este egal cu numarul de linii a celei de-a doua. Alocarea memorie pentru matricea rezultat c este realizata in momentul apelarii constructorului cu parametrii matrice c(n,b.m).

Operatia de adunare este realizata in cadrul clasei matrice prin supraancarcarea operatorului "+". Aceasta este realizata astfel:

matrice matrice::operator +(matrice b)

return c;

Procedura primeste ca parametrii de intrare pionterul this si un obiect de tip matrice, b. Rezultatul adunarii este pus in obiectul c. Asemenea operatiei de inmultire pointerul this este operandul stang al adunarii, iar obiectul de tip matrice, b este operandul drept al operatiei.

Operatia de scadere este realizata in cadrul clasei matrice prin supraincarcarea operatorului "-". Aceasta este realizata astfel:

matrice matrice::operator -(matrice b)

return c;

Procedura primeste ca parametrii de intrare pionterul this si un obiect de tip matrice si anume b. Rezultatul scaderii este reprezentat de obiectul c. Pointerul this este operandul stang al diferentei, iar obiectul de tip matrice, b este operandul drept al operatiei de scadere.

In clasa matrice operatia de transpunere este realizata prin supraincarcarea operatorului "!". Supraincarcarea este realizata astfel:

matrice matrice::operator!()

Procedura de supra-incarcare intoarce un obiect de tip matrice si anume rezultatul transpunerii matricei, care este creat in interiorul procedurii, obiectul b. Procedura primeste ca parametru de intrare un pointer la un obiect de tip matrice, pointerul this. Acesta reprezinta operandul din partea dreapta a transpunerii. Alocarea memorie pentru matricea rezultat c este realizata in momentul apelarii constructorului cu parametrii, matrice b(n,m).

In clasa matrice copierea unei matrice intr-o alta matrice este realizata prin supraancarcarea operatorului "=". Supraincarcarea se realizeaza astfel:

matrice& matrice ::operator =(matrice b)

Functia intoarce un obiect de tip matrice, care este transferat prin referinta; in exemplul de mai sus acest obiect este pointerul this. Parametrul de intrare este reprezentat de obiectul b, iar paramerul de iesire este pointerul this.

4 Functii de prelucrare

Functiile de prelucrare in matrice sunt acele functii care fac diferite operatii matematice, operatii de interschimbare, numarare, modificare, stergere, inlocuire asupra elementelor unei matrice modificand-o in cele mai multe cazuri.

Urmatoarele 2 functii primesc ca date de intrare pointer la obiectul de tip matrice, pointerul this si indicele liniei sau coloanei de sortat. Functiile sunt bubble_sort_linie si bubble_sort_coloana si ele sorteaza o linie respectiv coloana a matricei prin metoda bulelor. Cum aceste doua functii nu modifica dimensiunile matricei si lucreaza doar cu valorile elementelor matricei, functiile nu returneaza nici o valoare.

Prima funtie este :

void matrice::bubble_sort_linie(int line)

k=0;

}

} while (k==0);

iar ce de-a doua functie este :

void matrice::bubble_sort_coloana(int column)

k=0;

}

} while (k==0);

Functiile void sume_linii si sume_coloane afla suma elementelor matricei de pe fiecare linie, respectiv de pe fiecare coloana. Pe langa pointerul implicit this la obiectul de tip matrice apelator, functiile primesc o referinta la o variabila de tip int. Aceasta este utilizata pentru a memora dimensiunea vectorului de sume, implicit vectorul rezultat are dimensiunea egala cu numarul de linii, in cazul sumelor elementelor de pe fiecare linie, respectiv numarul de coloane al matricei, pentru cazul determinarii sumelor elementelor de pe fiecare coloana.

Functiile sunt :

int * matrice::sume_linii(int & lenght)

lenght=n;

return v;

si respectiv :

int * matrice::sume_coloane(int & lenght)

lenght=m;

return v;

Urmatoarea pereche de functii interschimbare_lines si interschimbare_columns interschimba doua linii, respectiv doua coloane ale matricei intre ele. Cele doua functii apartin clasei matrice si au ca parametrii de intrare pozitiile in matrice al celor doua linii, respectiv coloane, care se interschimba. In interiorul functiilor se realizeaza validarea acestor pozitii.

Cele doua functii sunt :

void matrice::interschimbare_lines(int line1,int line2)

void matrice::interschimbare_columns(int column1,int column2)

Cele doua functii care urmeaza sortare_coloane() si sortare_linii() sorteaza coloanele, respectiv liniile matricei in functie de suma elementelor lor. Pentru a face acest lucru functiile vor apela functia care calculeaza sumele dupa care se sorteaza, adica sume_coloane si lines_sort, si functia de interschimbare a doua coloane/linii.

Functiile nu returneaza nici o valoare, ci doar modifica valorile elementelor matricei.

Functiile sunt :

void matrice::sortare_coloane()

}

void matrice::sortare_linii()

}

Functiile de prelucrare a elementelor unei matrice sunt foarte variate si sunt impuse de natura rezultatelor.

5 Liniarizarea matricelor

O mare aplicabilitate o are operatia de vectorizare sau liniarizare a unei matrice. Aceasta este concretizata in lucrarea de fata, prin int* liniarizare_matrice(int *k) din cadrul clasei matrice.

Aceasta functiei preia o matrice cu n linii si m coloane si o transforma intr-un vector de n*m+2 componente. Traversarea matricei se face pe linii, deci in vector regasirea elementelor matricei este echivalenta cu punerea cap la cap a fiecarei linii. Dimensiunea vectorului este cu doua componente mai mare decat numarul de elemente ale matricei deoarece pe ultimele doua pozitii se pastreaza numarul de linii, respectiv numarul de coloane ale matricei. Este importanta pastrarea dimensiunilor matricei pentru o eventuala operatie inversa, de la vector la matrice sau pentru operatiile de adunare, scadere, transpunere si inmultire cu matrice vectorizate.

Functia de liniarizare este functie membra a clasei si are tipul int* returnand asadar un vector. Deoarece atat vectorul cat si matricea sunt implementate dinamic, alocarea memorie necesare vectorului rezultat se realizeaza in interiorul functiei.

int* matrice::liniarizare_matrice( int *k)

x[*k]=n;

(*k)++;

x[*k]=m;

(*k)=(n*m)+2;

return x;

Functia care realizeaza insumarea a doua matrice vectorizate se numeste suma_matrice_liniarizate. Ea are urmatoarea forma int * suma_matrice_liniarizate(int *, int, int *, int, int *). Functia este are tipul int* pentru ca returneaza un vector, ce reprezinta matricea suma liniarizata. Functia are urmatorii parametrii:

parametrii de intrare sunt int *x, int *y reprezentand matricele care au fost vectorizate, respectiv vectorii in care au fost transformate;

int n1, dimensiunea vectorului x;

int n2, dimensiuena vectorului y;

int *k care reprezinta adresa vaariabilei ce memoreaza dimensiunea vectorului rezultat al adunarii vectorilor x si y.

Suma a doua matrice liniarizate se rezuma la suma a doi vectori, insa trebuie acordata atentie ultimelor doua elemnte din fiecare vector, care reprezinta dimensiunile matricelor.Functia este:

int * suma_matrice_liniarizate( int *x,int n1, int *y, int n2, int *k)

return z;

Inmultirea a doua matrice vectorizate este realizata de functia int* inmultire_matr_liniarizate(int *,int ,int *, int ,int *). Subprogramul primeste cele doua matrice liniarizate si dimensiunile lor si returneaza matrice rezultat liniarizata, precum si dimensiunea ei. Algoritmul utilizeaza variabilele vb si vb1 pentru a verifica momentul terminarii componentelor matricei. Altfel, exista riscul inluderii in procesul de inmultire a ultimelor doua pozitii din fiecare vector, ce reprezinta numarul de linii si coloane asociate matricelor liniarizate.

int * inmultire_matr_liniarizate(int *x,int nr_elem_x,int *y, int nr_elem_y,int *k)

vb1=0;

while ((vb1*ny)!=(ny*my))

vb1++;

(*k)++;

}

vb++;

}

rez[*k]=nx;

(*k)++;

rez[*k]=my;

*k=my*nx+2;

}

else *k=0;

return rez;

Functia precedenta apeleaza la randul sau doua alte subprograme, matrice matrice_liniarizata_la_matrice(int *x, int dim) pentru a realiza operatia inversa liniarizarii si subprogramul, int * transpunere_matrice_liniarizata(int *,int , int *) pentru a transpune o matrice liniarizata dupa linii.

Subprogramele sunt:

matrice matrice_liniarizata_la_matrice(int *x, int dim)

return rez;

int * transpunere_matrice_liniarizata(int *x,int dim, int *k)

Functia matrice_liniarizata_la_matrice este declarata ca fiind friend in clasa matrice pentru a avea acces la constructorii acesteia.