| CATEGORII DOCUMENTE |
MEMORAREA ELECTRONICA A INFORMATIEI BINARE
In calculator se folosesc atat suporturi magnetice cat si electronice pentru stocarea pe o perioada scurta sau pe o perioada indelungata a informatiei binare. Memoriile magnetice (hard disck-ul, disckette-le, etc.) nu fac parte din calculatorul propriu-zis, ele constituind componente periferice importante, dar care nu participa direct la procesul de prelucrare a informatiei prin executia instructiunilor din program. In procesul de executie, programul se afla intr-o memorie electronica unde-i stocat sub forma de coduri binare de tip instructiune si de tip date. In decursul prelucrarii procesorul extrage din memorie cate un cod tip instructiune si-l aduce in procesor unde il interpreteaza si-l executa dupa care extrage din memorie urmatoarea instructiune etc.
Durata executiei unei instructiuni, Ti, are doua componente:
Timpul de prelucrare Tprel este folosit de procesor pentru decodificare si executia operatiei definite in codul respectiv al instructiunii. Timpul de acces Tacces este timpul scurs din momentul la care procesorul solicita de la memorie eliberarea unui anumit cod pe magistrala si pana la prezenta lui pe magistrala (extractia). Acest Tacces trebuie sa fie mai mic decat perioada de tact, T a ceasului procesorului. Daca frecventa de ceas a procesorului este f = 100 MHz, atunci timpul de acces la memorie trebuie sa fie sub 0.001 microsecunde. Progresul tehnologiilor de fabricatie a memoriei a condus la timpi de acces foarte mici.
Timpul de acces foarte mare al memoriilor pe suport magnetic le-a facut de neutilizat ca memorii operative in calculatoarele actuale, la care viteza de prelucrare a informatiei binare este esentiala.
Memoria electronica din calculator este structurata pe OCTETI. Fiecare octet de memorie este o LOCATIE la ADRESA careia se poate memora un cod binar de 8 biti. Adresa fiecarei locatii este exprimata printr-un cod binar. Daca memoria respectiva are o capacitate de 64 Kocteti sunt necesare 64x1024=65536 adrese distincte, adica 216 adrese. Pentru obtinerea acestui numar de coduri binare de adrese sunt necesari 16 biti, se spune ca aceasta este lungimea codului de adresare a memoriei. Exprimate HEXA aceste adrese vor fi: 0000H; 0001H; 0002H; ; FFFEH; FFFFH.
Fiecare locatie de cate 1 octet este compusa din 8 celule de memorie de un bit realizata pe baza unui circuit electronic elementar de memorie numit BISTABIL. Denumirea lui vine de la faptul ca acesta poate ramane in starea cu unu la iesire sau cu zero la iesire dupa inscriere, deci poate memora.
Comunicatia procesorului cu memoria externa M se face prin grupuri de linii de legatura numite magistrale. De exemplu pentru transmisia paralela (simultana), de la procesor la memorie, a celor 16 biti de adresa se foloseste o magistrala de adrese care are 16 linii, ca in figura urmatoare. Aceste linii formeaza magistrala de adrese (mA) pe care sunt transmise catre memorie coduri sau 'cuvinte' cu 16 ranguri: A15, A14, A13, A12, , A3, A2, A1, A0.
Magistrala de date este grupul de linii pe care se face schimbul de informatii ale celor 2 entitati ale tandemului procesor - memorie. Pentru a transporta in paralel (simultan) toti cei 8 biti dintr-o locatie, magistrala de date (mD) are opt linii.
Spre deosebire de mA, pe mD transmisia informatiei se poate face in ambele sensuri:

Notatiile din figura au urmatoarele semnificatii:
ma - magistrala de adrese;
mC - magistrala de comenzi;
mD - magistrala de date;
M - memoria operativa;
RAM - random access memory;
ROM - read only memory;
m - memorie interna directa a procesorului (cache) formata din registre speciale si registre de serviciu (PC-ul, SP-ul, etc);
Fie CLC-ul din figura cu intrarile Ut si Xt care la momentul t iau valori in B= si iesirea Qt care la momentul t ia valori tot in .

In cazul CLC timpul nu intervine in comportarea logica a circuitului, ci numai valorile logice ale intrarilor. Daca, de exemplu, perechea X si U au la momentul t valori care determina trecerea lui Q din 1 in 0 se va considera ca aceasta trecere se face instantaneu. Aceasta presupunere nu influenteaza interpretarea corecta a comportarii CLC-lui. In realitate trecerea din 1 in 0 a lui Q nu are loc instantaneu, ci treptat intr-un interval de timp mic, dar totusi finit. Acest proces de coborare incepe la un moment anterior lui t pe care il notam t-1 si se termina la t.
Circuitul logic secvential (CLS) se obtine dintr-un CLC prevazut cu cel putin un circuit de reactie. Prin reactie se intelege o conexiune (circuit) prin care semnalul de iesire este aplicat la una din intrari. In aceste conditii, iesirea Qt va depinde nu numai de intrare ci si de valoarea iesirii la momentul precedent, ca in figura urmatoare in care facand Xt=Qt-1 rezulta Qt=f(Ut, Qt-1), in care f este functia logica a CLC-ului cu care s-a realizat CLS-ul.

Un asemenea circuit, la care iesirea Q la momentul t (notata Qt) depinde de Qt-1 (care exprima valoarea lui Q la momentul t-1 se spune ca are proprietate de memorare.
Bistabilul este un CLS elementar cu 2 stari stabile (Qt=0 si Qt=1). Trecerea dintr-o stare in alta se poate comanda prin intermediul semnalelor de intrare.
Proprietatea principala a bistabilului: Bistabilul are cel putin o valoare a intrarii (intrarilor) pentru care Qt=Qt-1. Nu este interzisa neunivocitatea ca 2 valori diferite ale acelorasi intrari sa provoace aceeasi stare Qt. Regula este: 'la intrari diferite iesiri diferite'. Principalele circuite bistabile au denumiri si reprezentari acceptate la nivel mondial. Tipurile cele mai uzuale de bistabili sunt: RS; JK; D; T. Reprezentarea unui bistabil se face prin: Simbol, tabel de stare si expresia ecuatiei de stare respectiv a functiei logice Qt=f( ) care-i descrie functionarea si care se deduce din tabelul de stare a bistabilului dat.
Semnalele de intrare: SET notat cu S si RESET notat cu R. Operatia de 'setare' a bistabilului semnifica aducerea in 1 a iesirii acestuia, iar 'resetarea' semnifica aducerea iesirii lui in 0.
Tabelul de stare descrie functia de iesire Qt=f a carui domeniu de definitie este x=BxB si care ia valori in :
|
intrari |
iesire |
|||
|
St |
Rt |
Qt |
||
|
linia 1: memorare |
→ |
0 |
0 |
Qt-1 |
|
linia 2: resetare |
→ |
0 |
1 |
1 |
|
linia 3: setare |
→ |
1 |
0 |
1 |
|
linia 4: interzisa |
→ |
1 |
1 |
1 |
Redefinirea functiei de iesire si conversia tabel de stare → tabel de adevar:
|
intrari |
iesire | |||
|
Qt-1 |
St |
Rt |
Qt | |
|
0 |
0 |
0 |
0 |
MEMORARE |
|
1 |
0 |
0 |
1 |
|
|
0 |
0 |
1 |
0 |
RESETARE |
|
1 |
0 |
1 |
0 |
|
|
0 |
1 |
0 |
1 |
SETARE |
|
1 |
1 |
0 |
1 |
|
|
0 |
1 |
1 |
1 |
INTERZISA |
|
1 |
1 |
1 |
1 |
|
Deoarece Qt-1 ia valori tot in se poate scrie Qt : BxBxB→. Aceasta conduce la urmatorul tabel de adevar al CLS-ului:
Diagrama K-h a bistabilului RS este urmatoarea:

|
00 |
01 |
11 |
10 |
|
|
0 |
0 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
1 |
In acest tabel se pot forma 2 grupuri: GR 1 de 4 celule cu a+b=2 caruia i se ataseaza 3-2=1 variabile adica numai S; GR 2 de 2 celule cu a+b=1 caruia i se ataseaza un produs de 3-1=2 variabie Qt-1(~R). Astfel rezulta ecuatia de stare a bistabilului RS:
![]()
Aplicand deMorgan se obtine:
![]()
![]()
Folosind inca o data deMorgan se obtine functia care permite implementarea numai cu AND-uri si NON-uri:
![]()
Simbolul de reprezentare in schemele logice ale circuitelor de calcul mai complexe, in care RS-ul este un element component, este un patrat cu 2 intrari (R si S) si 2 iesiri (Q si ~Q) astfel:

Observatie: pentru simplificarea scrierii, in continuare se va omite indicele t la variabilele R, S, J, K, D, T si Q.
J |
K |
Q |
|
0 |
0 |
Qt-1 |
|
0 |
1 |
0 |
|
1 |
0 |
1 |
|
1 |
1 |
|
Se observa ca intrarea de setare este acum J, iar cea de resetare este K si se mai observa ca a fost eliminata starea de neunivocitate (pe linia 4 din tabelul de stare a RS-lui). Se poate constata ca substituind in ecuatia RS-lui pe S si pe R cu
S=J(~Qt-1)
se obtine o ecuatie care satisface tabelul de stare al JK-lui. Deci aceasta este ecuatia de stare a JK-lui:
Q=J(~Qt-1)+( ~K)Qt-1
Din cele de mai sus rezulta ca CLS-ul care implementeaza ecuatia de stare a RS-lui se poate construi in jurul unui RS la care se adauga nonAND pentru formarea lui R=KQt-1 respectiv a lui S=J(~Qt-1) prin introducerea a 2 reactii suplimentare una dupa Q si alta dupa ~Q, ca in urmatoarea schema logica a JK-lui.


Simbolul JK-lui este similar cu cel al RS-lui cu deosebirea ca R si S sunt inlocuite cu K respectiv J.
BISTABILUL D (delay)
Acest bistabil are doar o intrare D si o iesire Q, care repeta intrarea: Q=D.
Tabelul de stare este:
D |
Q |
|
0 |
0 |
|
1 |
1 |
Ecuatia de stare rezulta din cea a JK-lui prin inlocuirea J=D si K=~D. Dupa inlocuire rezulta Q=D(~Qt-1 + Qt-1) in care paranteza este =1. Aceasta demonstreaza ca CLS-ul care implementeaza un bistabil D se poate obtine dintr-un JK prin aplicarea unui semnal D la borna de intrare J si a celui negat nonD la borna de intrare K. Semnalul de intrare apare la iesire cu intarzierea inerenta oricarui circuit fizic si deci Qt+1=Dt fapt pentru care se numeste 'delay'.
BISTABILUL T (trigger)
Acest bistabil are o singura intrare notata T si urmatorul tabel de stare:
|
T |
Q |
|
0 |
Qt-1 |
|
1 |
~Qt-1 |
Daca in ecuatia JK-lui se face J=K=T rezulta ecuatia care satisface tabelul de stare dat si prin urmare aceasta reprezinta ecuatia de stare a bistabilului T:
Q=T(~Qt-1)+(~T)Qt-1 '
Rezulta astfel ca CLS-ul de implementare a bistabilului T contine un JK cu intrarile legate intre ele la care se aplica T.
Simbolul este tot un dreptunghi cu o singura borna de intrare T si 2 de iesire: Q si ~Q.
CLS-ul are o iesire E prin care se poate citi DATA de 1 bit memorata acolo anterior momentului primirii prin mC a comenzii de READ de la procesor. Pe intrare celula trebuie sa poata primi 3 semnale binare provenite de pe cele 3 magistrale ale procesorului: un semnal de adresa A; un semnal de intrare date I; un semnal de validarea scrierii W. Toate aceste semnale sunt binare si asigura comunicatia cu procesorul prin cele 3 magistrale. Nucleul acestei celule poate fi un RS comandat pe intrare cu S=A&I&W=AIW si respectiv cu R=A&(~I)&W iar iesirea celulei E=Q&A unde Q este iesirea RS-lui din centrul celulei.
Seminar 1
Calculatoare
(1) Variabile de comutatie:
![]()
1 daca x = 1 sau y = 1,
sau x + y =
0 daca x = 0 si y = 0.
![]() 1 daca x = 1 si y = 1,
1 daca x = 1 si y = 1,
si x * y =
0 daca x = 0 sau y = 0.
![]()
1 daca x = 1,
sau ![]() =
=
0 daca x = 0.
Proprietati
x + 0 = x;
x + 1 = 1;
x * 0 = 0;
x * 1 = x;
![]() = x;
= x;
x +![]() = 1;
= 1;
x *![]() = 0;
= 0;
x (y + z)=xy + xz;
x + yz = (x + y)(x + z);
distributivitatea x(x + y) = xx + xy = x + xy;
x + xy = (x + x)(x + y) = x(x + y);
x + xy = x * 1 + xy = x(1 + y) = x * 1 = x.
Exemplu
x +![]() y = x
+ y
y = x
+ y
x +![]() y = (x +
y = (x +![]() )(x + y) = 1(x + y) = x + y
)(x + y) = 1(x + y) = x + y
Sa se demonstreze 9
|
Xyz |
x+yz |
(x+y)(x+z) |
x(![]() + y) = xy
+ y) = xy
x![]() + xy = xy
+ xy = xy
xy +![]() z + yz = x y+
z + yz = x y+![]() z
z
xy +![]() z - yz*1 = xy +
z - yz*1 = xy +![]() z + (x +
z + (x +![]() )(yz) =
)(yz) =
xy +![]() z + yzx + yz
z + yzx + yz![]() = xy(1 + z) +
= xy(1 + z) + ![]() z(1 + y) =
z(1 + y) =
xy +![]() z.
z.
Sa se calculeze complementarele functiilor:
![]()
|
|
![]()
=(![]() +y)+
+y)+ ![]() =
=![]() +y+
+y+![]() .
.
![]() x+
x+![]() +z)*
+z)*![]() = (x+
= (x+![]() +z)(
+z)(![]() +
+ ![]() )=
)=
=x![]()
![]()
![]() +z
+z![]() +x
+x![]()
![]()
![]() +z
+z![]()
![]()
![]() +z
+z![]() +x
+x![]()
![]() +z
+z![]()
![]()
![]() +x+1+z)+z
+x+1+z)+z![]()
![]() +z
+z![]()
(2)
![]()
=[![]() ][
][![]() ]=(x+z+
]=(x+z+![]() )(
)(![]() +z)=
+z)=

(a + c)(a + d)(b + c)(b + d) = ab + cd
(aa + ac + ad + cd)(bb + cb + bd + cd) =
(a(1 + a + cd) + cd)(b(1 + c + d) + cd) = (a * 1 + cd)(b * 1 + cd) =
=(a + cd)(b + cd) = ab + acd + cbd + cd = ab + cd.
Tema
1) ![]() ;
;
2) ![]()
Sa se simplifice:
1)
![]()
2)
![]()
3)

Tema

Sa se afle
complementarele ![]() simplificare:
simplificare:

Tema
Complementare si simplificare:
![]()
Tabela de adevar si sa se considere formulele Σ mintermeni si produsul de maxtermeni pentru functii si pentru complementarele lor.
|
xy |
f |
![]()
f1![]() suma de produse
suma de produse
f1![]() produs de sume
produs de sume
f1![]()
f1![]()
![]()
|
xyz |
f |
Σ mintermeni

Pentru acasa:
f3![]() tabela
tabela
1)
![]()
![]() (1 + c) +
(1 + c) + ![]()
![]() (1 + b) + bc =
(1 + b) + bc = ![]() + bc [ab +
+ bc [ab + ![]() c]
c]
2)
![]()
3)
![]()
f (w ,x, y, z) =xy(1 + z)![]()
![]() (x + 1) + wx (1 + y) =
(x + 1) + wx (1 + y) = ![]()
4)
![]()
5)
![]()
6)
![]()
7)
![]()
|
xyzw |
f |



|
x1 |
x2 |
x3 |
x4 |
cifra |
a |
b |
c |
d |
e |
f |
g |
|
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
|
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
2 | |||||||
|
0 |
0 |
1 |
1 |
3 | |||||||
|
0 |
1 |
0 |
0 |
4 | |||||||
|
0 |
1 |
0 |
1 |
5 | |||||||
|
0 |
1 |
1 |
0 |
6 | |||||||
|
0 |
1 |
1 |
1 |
7 | |||||||
|
1 |
0 |
0 |
0 |
8 | |||||||
|
1 |
0 |
0 |
1 |
9 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
![]()
|
|
00 |
01 |
11 |
10 |
|||
|
00 |
1 |
0 |
- |
1 |
|||
|
01 |
0 |
1 |
- |
1 |
|||
|
11 |
1 |
1 |
- |
1 |
|||
|
10 |
1 |
1 |
- |
- |
pentru a



f = xy + wz cu NAND:
![]()
![]()
Proprietate: doua numere succesive difera printr-un singur bit.
|
cod binar |
cod Gray |
|||||||||
|
x3 |
x2 |
x1 |
x0 |
y3 |
y2 |
y1 |
y0 |
|||
|
|
- |
0 |
0 |
0 |
0 |
- |
0 |
0 |
0 |
0 |
|
1 |
- |
0 |
0 |
0 |
1 |
- |
0 |
0 |
0 |
1 |
|
2 |
- |
0 |
0 |
1 |
0 |
- |
0 |
0 |
1 |
1 |
|
3 |
- |
0 |
0 |
1 |
1 |
- |
0 |
0 |
1 |
0 |
|
4 |
- |
0 |
1 |
0 |
0 |
- |
0 |
1 |
1 |
0 |
|
5 |
- |
0 |
1 |
0 |
1 |
- |
0 |
1 |
1 |
1 |
|
6 |
- |
0 |
1 |
1 |
0 |
- |
0 |
1 |
0 |
1 |
|
7 |
- |
0 |
1 |
1 |
1 |
- |
0 |
1 |
0 |
0 |
|
8 |
- |
1 |
0 |
0 |
0 |
- |
1 |
1 |
0 |
0 |
|
9 |
- |
1 |
0 |
0 |
1 |
- |
1 |
1 |
0 |
1 |
|
10 |
- |
1 |
0 |
1 |
0 |
- |
1 |
1 |
1 |
1 |
|
11 |
- |
1 |
0 |
1 |
1 |
- |
1 |
1 |
1 |
0 |
|
12 |
- |
1 |
1 |
0 |
0 |
- |
1 |
0 |
1 |
0 |
|
13 |
- |
1 |
1 |
0 |
1 |
- |
1 |
0 |
1 |
1 |
|
14 |
- |
1 |
1 |
1 |
0 |
- |
1 |
0 |
0 |
1 |
|
15 |
- |
1 |
1 |
1 |
1 |
- |
1 |
0 |
0 |
0 |
Calculatoare
![]()
![]()
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
0 |
|
0 |
1 |
0 |
1 |
0 |
|
0 |
1 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
0 |
1 |
|
1 |
1 |
0 |
0 |
1 |
|
1 |
1 |
1 |
1 |
1 |
|
AiBi | |||||
|
Ti-1 | |||||
|
0 |
pt. Si |
||||
|
1 |
|
AiBi | |||||
|
Ti-1 | |||||
|
0 |
pt. Ti |
||||
|
1 |
![]()
![]()
![]()
![]()
Introduceti valorile Ti in tabela:
|
| |||
|
|
0 |
1 |
|
|
0 |
|
|
|
|
1 |
|
|
|
|
|
|
| |||
|
|
0 |
1 |
|
|
0 |
0 |
|
|
|
1 |
|
1 |
|
|
|
![]()
![]()
Se implementeaza sumatorul complet in functie de schema sumatorului


![]()
![]()
![]()
x
 y
y
Circuite MSI
Sumatorul de 4 biti paraleli( 7483);
Decodificator 74154( 4:16);
Multiplexorul 74150, 1, 3, 5, 7.
Sumator in zecimal codificat binary( ZVB)
pp. reprezentarea fiecarui rang al unei cifre zecimale in binary. Rangul se reprezinta pe o tetrada( 4 biti).
![]()
![]()
![]()
reprezentarea nr. In ZCB este necesara cand avem iesiri din circuit pe tuburi
Sumator complet paralel de 4 biti( 7483)
Pentru numere mai mari de 9 este necesara corectie; pentru nr.<=9 nu este necesara.
0000-------- ----- ------ --------0
-
-
1001-------- ----- ------ --------9
1010(B)![]() ZCB
ZCB
1010
0110
10000
|
Sumele necorectate |
Sumele corectate |
||||||||
|
Tc |
|
T |
|
|||||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
|
|
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
|
|
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
|
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
|
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
|
|
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
|
|
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
|
|
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
|
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
|
|
A |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
|
B |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
|
C |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
|
D |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
|
E |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
|
F |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
![]()
![]()


![]()
celula elementara de adunare 2 unitati zecimale reprezentate in ZCB devine


Decodificatorul 4:16
![]() combinatii pentru marimi de intrare prestabilite
combinatii pentru marimi de intrare prestabilite
16 pentru functiile de iesire
|
|
|
|
|
|
|
|
|
----- ----- ---------------- |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
|
|
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
|
|
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
|
|
0 |
0 |
1 |
1 |
. |
1 |
1 |
1 |
1 |
|
|
0 |
1 |
0 |
0 |
. |
1 |
1 |
1 |
1 |
|
|
0 |
1 |
0 |
1 |
. |
1 |
1 |
1 |
0 |
|

Strobe= 0 Enable 1Deseable
Tema : Sa se implementeze functia :
![]()
![]()
Utilizand decodificatorul 3:8. Indicatie: in cazul codificatoarelor implementarea cu acest tip de . este utila cand avem un numar mare de functii de iesire si un numar relative mare de mintermeni.
Sa se indice succesiunea de stari in f(CLK)

![]()
![]()
![]()
|
s. curenta |
s. urmatoare |
|
|
|
D |
Q(t+1) |

![]()
![]()
![]()
![]()
|
|
|
|
00 | |
|
A |
B |
C |
|
|
|
|
|
|
|
|

|
|
|

|
T |
Q(t+1) |
|
Q(t) |
|
|
Q(t) |
![]()
![]()
![]()
|
|
|
Se considera ![]()
Sa se realizeze. unul de tip D si unul de tip T.
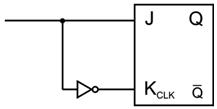
|
JK |
Q(t+1) |
|
Q(t) |
|
|
Q(t) |
|
D |
(J) | |
|
Q | ||
|
D |
(K) | |
|
Q | ||
![]()
|
T |
(K) | |
|
Q | ||
|
T |
(J) | |
|
Q | ||
J=T
K=T
|
T |
Q(t+1) |
|
Q(t) |
|
|
|
|
J |
K |
Q(t+1) |
|
Q(t) |
||
|
|
Sa se proiecteze un circuit monoimpuls folosind ASM


|
| ||
|
| ||
|
A |
B |
|
|
C |
|
| ||
|
| ||
|
IA | ||
|
| ||
|
| ||
|
IA |
|
| ||
|
| ||
|
IA | ||
![]()
![]()

|
| ||
|
| ||
MI=![]()

|
| ||
|
| ||
|
| ||
|
|
|
| ||
|
| ||
|
|
![]()
|
| ||
|
| ||
|
IA | ||
|
|
|
| ||
|
| ||
|
|

Calculatoare
Numarator sincron cu succesiunea starilor.
 000
000
100
110
111
011
000
|
| ||||
|
| ||||
|
A |
C |
B |
||
|
E |
D | |||
|
| ||||
|
| ||||
|
| ||||
|
| ||||
|
| ||||
|
| ||||

![]()
|
tranzitia |
j |
k |
|
| ||
|
| ||
|
| ||
|
|
|
|
| |||
|
| ||||
|
|
| |||
|
| ||||
|
|
| |||
|
| ||||
|
| ||||
![]()


Numarator sincron reversibil cu JK, 4 stari: - ![]() comanda descrescatoare;
comanda descrescatoare;
-
![]() comanda creascatoare.
comanda creascatoare.

|
| ||
|
| ||
|
A |
C |
|
|
B |
D |
|
|
b |
| |
|
a | ||
|
| ||
|
|
|
b |
| |
|
a | ||
|
|
||
|
|
|
|
|
|
![]()
![]()
![]()
![]()
|
b | ||
|
a | ||
|
| ||
|
|
|
b |
| |
|
a | ||
|
|
||
|
|


2. CSS cu y1, y2 sinc. Si Q1 si Q2. Pt. Y1Y2..

Realizarea circuitelor de comutatie combinationale cu circuite integrate de tip LSI
O memorie ROM (memorie permanenta) este un dispozitiv care contine atat decodificatorul cat si portile SAU necesare pentru realizarea unor functii de comutatie. Fixarea conexiunilor intre iesirile decodificatorului si intrarile portilor SAU deci fixarea functiilor de comutatie realizate de un astfel de dispozitiv se face prin "programarea" memoriei. Inregistrarea informatiei intr-o memorie ROM (programarea memoriei) se face prin fabricatie sau in cazul memoriilor PROM cu ajutorul unui dispozitiv special numit "programator de PROM-uri".Schema bloc a unei memorii ROM este:
![]()
![]()
![]()
n intrari m iesiri
![]()
![]()
Memoria are n intari. Fiecare
combinatie de valori a semnalelor de intrare se numeste adresa. Fiecare
combinatie de valori a semnalelor de iesire se numeste cuvint. Numarul de biti
intr-un cuvant este n fiind egal cu numarul de iesiri. Fiecare adresa reprezinta
de fapt un mintermen realizat cu cele n semnale de intrare. Un cuvant este
selectat de o adresa unica si este format din valorile functiilor de comutatie
implementate pentru combinatia de valori reprezentata de adresa respective.
Deci vor exista 2n cuvinte
memorate in ROM. Valorile obtinute la un moment dat la iesirile memoriei
reprezinta cuvintul selectat de adresa aplicata la intrarile circuitului. Sa
consideram de exemplu o memorie de ![]() ROM. Structura interna
echivalenta a unei astfel de memorii este:
ROM. Structura interna
echivalenta a unei astfel de memorii este:
Decodificator 2 la 4
00
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 01
01
![]()
![]()
![]()
![]()
![]() 10
10
11

![]()
![]()
![]()
![]()
Prin stabilirea legaturilor intre
iesirile decodificatorului si intrarile portilor SAU se stabilesc funtiile
realizate de catre acest circuit combinational. Sa consideram de exemplu
implementarea functiilor: ![]() si
si ![]() . Se observa ca structura interna echivalenta a memoriei ROM
trebuie sa devina
. Se observa ca structura interna echivalenta a memoriei ROM
trebuie sa devina
Decodificator 2 la 4![]()
00
![]()
![]()
![]()
![]()
![]()
![]()
![]() 01
01
![]()
![]()
![]()
![]()
![]() 10
10
11

![]()
![]()
![]()
![]()
In general implementarea unor functii de comutatie cu ajutorul unei memorii PROM parcurge urmatoarele etape:
in functie de numarul de functii care se realizeaza se stabileste lungimea minima a cuvantului de memorie;
in functie de numarul de variabile pentru functiile de comutatie implementate se stabileste numarul minim de intrari;
pe baza lungimii minime a cuvantului si a numarului de intrari se allege un anumit tip de circuit ROM;
Se observa ca ![]() si
si ![]() si deci este necesar
sa se realizeze numai un circuit combinational care sa utilizeze functiile
si deci este necesar
sa se realizeze numai un circuit combinational care sa utilizeze functiile ![]() . Rezulta ca se poate utiliza o memorie PROM cu urmatoarea
tabela da adevar.
. Rezulta ca se poate utiliza o memorie PROM cu urmatoarea
tabela da adevar.
|
A |
A |
A |
F |
F |
F |
F |
Utilizarea memoriilor ROM (PROM) pentru implementarea functiilor de comutatie este avantajoasa atunci cand se realizaeza un numar relativa mare de functii de comutatie cu un numar mare de variabile de intrare.
Sa incercam sa utilizam insa 6
memorii de tip ROM pentru realizarea conversiei de la codul utilizat pentru
reprezentarea caracterelor pe cartele perforate la un cod de tipul celor pentru
reprezentarea numerelor in calculatoarele numerice (ASCII). Codul utilizat
pentru reprezentarea caracterelor pe cartelele perforate utilizeaza 12 valori
binare (biti), fiecare valoare fiind asociata unei linii de pe cartela.
Codurile utilizate pentru reprezentarea caracterelor in calculatoarele numerice
sunt coduri care utilizeaza 8 biti. Rezulta ca o memorie ROM utilizata pentru o
astfel de aplicatie ar trebui sa fie de tipul 4096 x 8 (![]() ). Dintre cele 4096 de cuvinte din memorie sunt utile numai
47 (26 litere, 10 cifre, 11 semne speciale), celelalte cuvinte sunt associate
unor adrese (combinatii de valori ale semnalelor de intrare) care nu vor fi
aplicate niciodata la intrarea circuitului, cu alte cuvinte sunt combinatii de
valori pentru care functiile de comutatie realizate de circuit sunt nespecificate.
Rezulta deci o utilizare foarte ineficienta a memoriei. Intr-o astfel de
situatie se poate utiliza pentru implementarea functiilor de comutatie. Un alt
tip de circuit integrat de tip LS si anume circuite integrate de tip PLA. Un
circuit PLA este foarte asemenator ca structura echivalenta cu o memorie ROM.
Diferenta consta din faptul ca in locul decodificatorului apar o serie de porti
si, fiecare putind sa produca un produs de variatie in forma directa sau
complementata. Fixarea termenilor produsi de portile SI ( .. Intrarilor aplicate portilor SI) si a conexiunilor de
comutatie realizate de catre PLA. Schema bloc echivalenta a uni PLA cu n
intrari si M iesiri este:
). Dintre cele 4096 de cuvinte din memorie sunt utile numai
47 (26 litere, 10 cifre, 11 semne speciale), celelalte cuvinte sunt associate
unor adrese (combinatii de valori ale semnalelor de intrare) care nu vor fi
aplicate niciodata la intrarea circuitului, cu alte cuvinte sunt combinatii de
valori pentru care functiile de comutatie realizate de circuit sunt nespecificate.
Rezulta deci o utilizare foarte ineficienta a memoriei. Intr-o astfel de
situatie se poate utiliza pentru implementarea functiilor de comutatie. Un alt
tip de circuit integrat de tip LS si anume circuite integrate de tip PLA. Un
circuit PLA este foarte asemenator ca structura echivalenta cu o memorie ROM.
Diferenta consta din faptul ca in locul decodificatorului apar o serie de porti
si, fiecare putind sa produca un produs de variatie in forma directa sau
complementata. Fixarea termenilor produsi de portile SI ( .. Intrarilor aplicate portilor SI) si a conexiunilor de
comutatie realizate de catre PLA. Schema bloc echivalenta a uni PLA cu n
intrari si M iesiri este:
Se observa ca cele n intrari se vor aplica in forma directa sau complementata la intrarile portilor SI in functie de conexiunile fixate la intrarile portilor SI, iar pentru fiecare poarta SAU se utilizeaza toate cele x iesiri de porti SI sau numai o parte din ele. La iesirile circuitului se obtine fiecare functie implementate in forma directa daca se utilizeaza iesire directa de la poarta SAU corespunzatoare sau in forma complementata daca se utilizeaza iesirea unei porti NU legata la iesirea portii SAU corespunzatoare.
Tipul circuitului PLA este dat de numarul de intrari, numarul de porti SI si numarul de iesri. Un exemplu tipic de circuit PLA are 16 intrari, 48 de porti SI, 8 iesiri.
Ca si in cazul memoriilor ROM fixarea functiilor realizate se obtine in fabricatie sau prin 'programare' cu ajutorul unor dispozitive speciale (in acest caz circuitele PLA sunt de tip FPLA).
Utilizaera circuitelor PLA este avantajoasa in cazul implemantarii unui numar mare de functii de comutatie cu un numar mare de intrari, daca numarul de combinatii de valori pentru care toate functiile sunt nespecificate este suficient de mare.
Peantru a ilustra tehnicile utilizate pentru implementarea cu ajutorul circuitelor de tip PLA vom prezenta din considerente didactice un exemplu mai simplu care nu respecta conditia precizata anterior. Fie functiile de comutatie de 3 variabila f1 si f2 reprezentate
de urmatoarele tabele Karnaugh.
|
Xy | ||||
|
Z | ||||
|
xy | ||||
|
z | ||||
![]()
![]()
Cele doua functii se pot realiza prin utilizarea unui PLA cu 3 intrari, 3 porti SI si doua iesiri, configurat in modul urmator:
x

![]()
![]()
 y
y
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
 z
z
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Specificarea modului de implemantare pentru un PLA nu se face bineinteles desenand structura echivalenta. Se construieste o tabela speciala pentru programarea circuitului PLA. Aceasta tabela este formata din doua tipuri de intrari:
intrari care descriu produsele realizate de catre fiecare poarta SI
si intrari care descriu sumele realizate de catre fiecare poarta SAU.
Se observa ca pentru fiecare poarta SI exista n intrari (corespunzatoare fiecarui semnal de intrare), fiecare intrare poate avea valorile 1,0,-.
Daca o variabila se conecteaza direct (complementat) valoarea intrarii este 1(0), daca o
variabila m se conecteaza la poarta respectiva valoarea este '-'. Se observa ca pentru fiecare poarta SAU exista x intrari (corespunzatoare fiecarei porti SI), fiecare intrare poate avea valoarea 1 sau -. Daca iesirea portii SI se conecteaza la intrarea portii SAU, cu alte cuvinte produsul respectiv participa la formarea sumei atunci valoarea intrarii este 1, altfel este ****. Pentru fiecare iesire de poarta SAU se precizeaza daca preluarea se face in forma directa sau complementara.
Se considera si urmatorul exemplu. Sa se cinstruiasca o realizare cu PLA pentru functiile de comutatie definite de urmatoarele tabele Karnough:
|
Xy | ||||
|
Z | ||||
|
xy | ||||
|
z | ||||


Se observa ca numarul minim de produse diferite pentru cele doua functii se obtine daca se
alege pentru f1 forma complementata, iar pentru f2 forma directa. Implementarea necesita un PLA cu 3 intrari, 4 porti SI si 2 iesiri. Tabela pentru programarea PLA-ului este:
|
porti SI |
Porti SAU |
||
|
intrari |
intrari |
||
|
produs |
x y z |
|
|
|
|
0 - |
1 |
|
|
|
- 0 |
- |
|
|
|
0 0 |
1 |
|
|
|
1 1 |
1 |
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2205
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved