Metode de programare

- Elemente de combinatorica -

1. Permutari

Fie . Sa se scrie un program recursiv de generare a permutarilor de ordin n. De exemplu, pentru n = 3, programul va genera:

2 3

3 2

1 3

3 1

1 2

2 1

Solutie: Permutarile de ordin n reprezinta toate posibilitatile de a aranja elementele unei multimi de n elemente. Permutarile de ordin n sunt functii bijective de forma:

a > . Reprezentam o astfel de functie printr-un vector a cu n componente avand semnificatia: a[i] este elementul asociat prin intermediul functiei a elementului i ().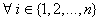

Conditii:

- ;

- .

Observatii:

In loc sa verificam pentru fiecare element i daca este sau nu un potrivit pentru pozitia k prin compararea lui i cu elementele deja fixate in vectorul a (a [l], a [2],, a[k - l]), am preferat sa optimizam functia de generare, utilizand o variabila globala suplimentara (sirul aux). Acesta reprezinta sirul caracteristic al multimii elementelor imagine ale functiei a (aux [ i ] este l daca elementul i a mai fost folosit, adica reprezinta deja imaginea unui element din multimea , respectiv 0, daca i nu a mai fost folosit). Cand plasam un numar i pe pozitia k, acesta reprezinta imaginea lui k prin intermediul functiei, deci aux [ i ] va deveni l. Cand revenim dintr-un apel recursiv, pe pozitia k urmeaza sa plasam un alt numar, deci i nu va mai fi imaginea lui k, prin urmare aux [ i ] trebuie sa redevina 0.

Numarul permutarilor de ordin n este: .

Aranjamente

Fie   cu . Sa se scrie un program recursiv care sa genereze aranjamentele de n elemente luate cate m. De exemplu, pentru n = 3 si m = 2, programul va genera:

2

3

1

3

1

2

Solutie: Aranjamentele de n elemente luate cate m reprezinta toate submultimile ordonate de m elemente ale unei multimi cu n elemente. Aranjamentele de n elemente luate cate m sunt functiile injective de forma: b: ->

Reprezentam o functie printr-un vector b, cu m componente, b [ i ] este elementul asociat prin intermediul functiei b elementului i   ().

Conditii:

- ;

- .

Singura diferenta dintre generarea permutarilor si generarea aranjamentelor consta in dimensiunea sirului solutie.

Numarul aranjamente de n elemente luate cate m este::

3. Combinari

Fie   cu . Sa se scrie un program recursiv care sa genereze combinarile de n elemente luate cate m. De exemplu, pentru n = 4 si m = 2, programul va genera:

2

3

4

3

4

4

Solutie: Combinarile de n elemente luate cate m reprezinta toate submultimile de m elemente ale unei multimi cu n elemente. Spre deosebire de aranjamente, ordinea elementelor din submultime nu conteaza. Din acest motiv, pentru a nu genera de mai multe ori aceeasi submultime (de exemplu, l 2 si 2 l), vom stabili o ordine convenabila pentru elementele submultimii si anume ordinea crescatoare.

Reprezentam o submultime printr-un sir c care contine cele m elemente ale submultimii, ordonate crescator.

Conditii:

- ;

- .

Conform celei de a doua conditii, pe pozitia k putem plasa doar elemente mai mari decat elementul plasat pe pozitia k- l (). Deci valoarea minima care poate fi plasata pe pozitia k este . Pentru ca aceasta formula sa fie valabila pentru orice pozitie k (inclusiv pentru   k = l) vom considera c [0] =0.

Deoarece dupa c[k] trebuie plasate inca m - k elemente mai mari decat c[k], se determina valoarea maxima care poate fi plasata pe pozitia k.

Valoarea maxima care poate fi plasata pe pozitia m este n, pe pozitia m - l este n - l s.a.m.d. Observam ca daca pozitia scade cu 1, si valoarea maxima care poate fi plasata pe pozitia respectiva scade cu l. Prin urmare, diferenta dintre pozitie si valoarea maxima care poate fi plasata pe pozitia respectiva este constanta (n - m). Deducem ca valoarea maxima care poate fi plasata pe pozitia k este n - m + k. Prin urmare, multimea numerelor posibile pentru pozitia k este .

Numarul de combinari de n elemente luate cate m este:

1. Permutari

#include <stdio.h>

#include <conio.h>

unsigned int n,a[30],aux[30];

void afisare()

void permutari(unsigned int k)

void main ()

Aranjamente

#include <stdio.h>

#include <conio.h>

unsigned int n,m,b[30],aux[30];

void afisare()

void aranjamente(int k)

void main ()

3. Combinari

#include <stdio.h>

#include <conio.h>

unsigned int n,m,c[30];

void afisare()

void combinari(unsigned int k)

void main ()

4. Permutari (varianta 2)

#include <stdio.h>

#include <conio.h>

unsigned int x[10],n;

void afisare()

unsigned int continuare (int k)

void back(unsigned int k)

}

void main()

5. Combinari (varianta 2)

# include <stdio.h>

# include <conio.h>

unsigned int a[100],n,k;

void initializari()

void afisare(int m)

int validare(int m)

void combinari(int m)

void main()