MS

 

Tema

Proiectrea unui filtru cu caracteristica arbitrara-functia yulewalk. Trasarea caracteristicii magnitudine-frecventa, comparare cu cea ceruta.. Testare cu semnal de intrare suma de doua frecvente, si, respectiv, cu o singura frecventa.

Functii utilizate:

[b,a]=yulewalk(ord,fr,m)

Este o functie pentru realizarea unui filtru IIR cu caracteristica arbitrara.

fr este un vector continand frecvente normalizate cuvalori crescatoare intre 0 si 1.

m reprezinta un vector cu aceeasi dimensiune ca si fr, continand valorile doritein caracteristica magnitudine-frecventa  (intre 0 si 1), la frecventele corespunzatoare din vectorul fr

- ord ordinal filtrului

[h,fre]=freqz(b,a,Np,fe)

Determina caracteristicilor magnitudine-frecventa si faza-frecventa.

-Np reprezinta numarul de puncte in care se va calcula caracteristica de transfer

a filtrului, H z

-fe reprezinta frecventa de esantionare,

-fr reprezinta un vector cu Np elemente avand valorile (in intervalul 0fe

-h reprezinta un vector cu Np elemente continand valorile functiei H z),calculate pentru valorile frecventei analogice f continute in vectorul fr

y=filter(b,a,x)

Determina caracteristica semnalului de iesire in functie de parametrii filtrului si de semnalul de intrare

Program MATLAB:

fr -frecventele determinante pentru filtu

Np=10000 -numarul de puncte

f=[100 200 300 400 500 600 700 800]

fe= -frecventa de esantionare

fn=fe/2 -frecventa normalizata

m=[0 0 0.7 1 1 0.7 0 0 1 1]

F=50

F1=100

t=0:0.001:0.1

t1=0:0.001:0.1

x=2*sin(2*pi*F*t) -semnal de intrare cu o singura frecventa

x1=2*sin(2*pi*F*t)+2*sin(2*pi*F1*t)-semnal de intrare suma de 2 frecvente

ord= -ordinul filtrului

[b,a]=yulewalk(ord,fr2,m) -functie de generare a filtrului

[h,fre]=freqz(b,a,Np,fe)

y=filter(b,a,x) -semnalul de iesire pentru intrare semnal cu o singura frecvanta

y1=filter(b,a,x1) -semnal de iesire pentru semnal suma de 2 frecvente

subplot(

plot(fre,abs(h)) -afiseaza caracteristica reala a filtrului

hold on

plot(fr,m) -afiseaza caracteristica ideala a filtrului

subplot(

plot(y)

subplot(

plot(y1)

Privire comparativa intre filtrele FIR si IIR

1. Filtrele IIR au cararcteristici similare cu cele ale FIR (latimea benzilor de tranzitie, atenuarile) dar pentru ordine de circa 4 ori mai mici, de exemplu 10 pentru IIR si 40 pentru FIR. Acest lucru inseamna aproximativ de 2 ori mai putine calcule pentru un filtru IIR (a se vedea expresia iesirilor celor doua filtre), daca consideram doar inmultirile, cele care consuma timp mai mult.

2. Filtrele FIR au caracteristica de faza liniara in functie de frecventa, in banda de trecere, in timp ce filtrele IIR au caracteristica neliniara. De aceea, pentru filtrele IIR, in cazul cand semnalul de intrare contine componente cu frecvente diferite, rezulta la iesire intarzieri diferite, ca numar de perioade, pentru semnalele de frecvente diferite, distorsionand semnalul de la iesire.

Daca se cunosc vectorii cu coeficientii filtrului:

b b b b bN], coeficientii numaratorului functiei de transfer, a a a a aN], coeficientii numitorului, cu a0 = 1 (la filtrele FIR vectorul a contine doar scalarul 1).

Daca x este vectorul cu semnalul de intrare al filtrului numeric, atunci semnalul de iesire este continut in vectorul y, care se determina prin functia filter

y filter b a x

Pentru determinarea caracteristicilor magnitudine-frecventa si faza-frecventa se foloseste functia freqz

h fr freqz b a Np fe), unde:

-Np reprezinta numarul de puncte in care se va calcula caracteristica de transfer a filtrului, H z), pentru z = exp(jW), cu W pf fe

-fe reprezinta frecventa de esantionare,

-fr reprezinta un vector cu Np elemente avand valorile (in intervalul 0fe

h reprezinta un vector cu Np elemente continand valorile functiei H z), calculate pentru valorile frecventei analogice f continute in vectorul fr

De asemenea, exista o functie pentru realizarea unui filtru IIR cu caracteristica arbitrara

b a yulewalk ord fr m), unde:

-fr este un vector continand frecvente normalizate cu valori crescatoare intre 0 (prima) si 1 (ultima),

-m reprezinta un vector cu aceeasi dimensiune ca si fr, continand valorile dorite in caracteristica magnitudine-frecventa (intre 0 si 1), la frecventele corespunzatoare

din vectorul fr

Concluzii:

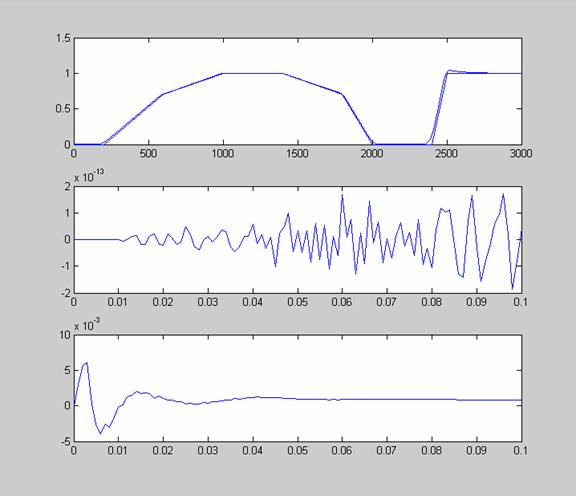
Parametrii de intrare:

-frecventele determinante pentru filtu

-frecventa de esantionare

-semnalele de testare a filtrelor x,x1

Parametrii de iesire:

-y, y2