A.S.P.C. - Multiplicator Wallace

A.S.P.C.

Multiplicator Wallace

Multiplicatorul folosind principiul Wallace Tree

Obiectivul acestui proiect este de a prezenta principiul de multiplicare folosind Wallace tree. In acest proiect am realizat un multiplicator pe 4 biti folosind acest principiu.

Cateva cuvinte despre multiplicarea digitala.

Multiplicarea digitala poate fi vazuta ca o serie de shiftari de biti si adunari, in care doua numere, inmultitorul si deinmultitul sunt combinate pentru obtinerea rezultatului final. Consideram multiplicarea a doua numere, multiplicatorul P si deinmultitul C, in care P este un numar pe n biti cu reprezentarea pe biti , cel mai semnificativ bit fiind pn-1 si cel mai nesemnificativ p0; C are o reprezentare similara . Pentru multiplicari fara semn, se aduna pana la n copii shiftate ale deinmultitului pentru a forma rezultatul. Toata procedura este divizata in 3 pasi: generarea produselor partiale (PP), reducerea produselor, si adunarea finala.Acestea sunt ilustrate conceptual in Fig. 1. Pentru a gasi o structura convenabila si rapida, ar trebui sa consideram diferite structuri ale multiplicatorului.

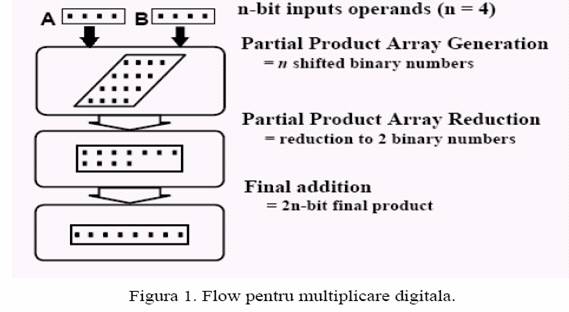
Generarea produselor partiale

Pasul initial in multiplicarea digitala este de a se genera n copii shiftate ale deinmultitului care se pot aduna ulterior in etapa urmatoare. Daca o copie data a denmultitului se aduna, aceasta depinde de valoarea bitului din inmultitor legata de aceasta copie. Daca bitul al i-lea (i =0 to n-1) al inmultitorului este '1', atunci se aduna versiunea shiftata cu i pozitii a deinmultitului.

Reprezentarea la nivel de bit a acestei functii se poate implementa utilizand o poarta logica AND, care realizeaza AND (ci,pj), i = 0 to n-1, j = 0 to n-1. Valorile rezultate suunt denumite biti de produse partiale sau, mai simplu, produse partiale; daca aranjam aceste produse partiale dupa pozitia bitilor din inmultitor, (bp = i + j), ajungem la o structura prezentata in Fig. 2. In aceasta proiectare, bitii produselor partiale sunt aranjati pe coloane; ei vor fi toti adunati pentru a forma valoarea finala. Structura trapezoidala rezultata este denumita vector de produse partiale (partial product array) sau mai simplu PPA. Acest pas este denumit generare de vectori de produse partiale (partial product array generation).

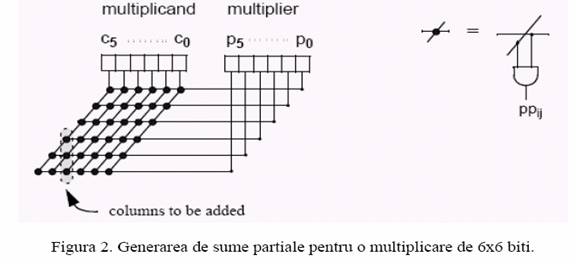
Sunt cateva aspecte importante referitoare la vectorul de produse partiale. In primul rand, in cea mai la baza formulare, (bitii PPA generati prin AND logic), toti bitii acestor produse partiale sunt generati in parallel; aceasta inseamna, ca intarzierea statica a tuturor bitilor este egala. In al doilea rand, dimensiunile vectorilor sunt functie de dimensiunea inmultitorului si a deinmultitului: inaltimea array-ului este proportionala cu dimensiunea inmultitorului, iar latimea este proportionala cu dimensiunea deinmultitului. In final, toti bitii intr-o coloana data trebuie adunati, si cateva coloane vor avea mai putini biti decat altele.

In mod concret, pozitiile bitilor de rang mai mic si cele ale bitilor de rang mai mare vor necesita mai putine adunari ca pozitiile bitilor din mijloc; cu putin mai multe adunari se vor efectua pe pozitiile de rang mare decat pe cele de rang mic, datorita faptului ca bitii de carry de pe pozitiile de rang mic se vor propaga spre pozitiile de rang mare.

Reducerea produselor partiale

Esenta unui multiplicator digital paralel eficient este maniera in care se aduna bitii PPA (din vectorul de produse partiale). In timp ce sumatoarele conventionale prezinta o intarziere masiva (din moment ce produsele partiale se adauga secvential la suma), metoda prezentata in continuare, numita carry-save addition reduce sumele partiale. Aceasta procedura permite ca adunari successive sa fie inglobate in doar un pas.

Consideram un vector de biti de forma: (bn-1, bn-2,,b1,b0), bi = . Daca dorim sa adunam doi biti din doi vectori de biti, sa spunem a0 si b0, din vectorii de biti a si b, putem utiliza FA ; primeste la intrare trei biti si produce un bit suma si unul de carry. Cand adunam doi vectori, se poate utiliza acest bloc pentru a aduna doi biti la o pozitie data, folosind carry-in de la precedenta adunare (bit). La pozitia cea mai nesemnificativa, se aduna doi biti si carry-out este propagat la pozitia urmatoare. De aici se combina carry-in si urmatorii doi biti de la pozitia urmatoare si se genereaza un carry-out. Utilizand aceasta tehnica de propagare a transportului, se observa ca adunarea a doua numere binare pe n-biti ia un ordin de O(n) adunari secventiale de doi biti. Prin urmare, intarzierea are un ordin de O(n).

Daca avem de adunat trei vectori de biti, A, B, si C, fiecare de dimensiune n, putem folosi aceasta tehnica pentru a aduna in primul rand pe A cu B, si apoi pe C cu rezultatul adunarii lui A cu B. Numarul adunarilor pe un bit este O(2n). Se observa ca daca utilizam aceasta tehnica in cea mai simpla forma, pentru a aduna n copii shiftate ale unui deinmultit pe n biti, intarzierea va fi de ordinal O(n²). Aceasta se intampla pentru ca presupunem ca operatiile de adunare sunt dependenta de precedentele adunari (iesirile de la operatiile care se efectueaza primele sunt intrari pentru operatiile de mai tarziu).

Se poate considera adunarea pentru o coloana; toti bitii dintr-o coloana trebuie adunati, impreuna cu bitii de carry-in din coloana precedenta. Intarzierea in calculul rezultatului la adunarea bitilor de pe o coloana este o functie de cand bitii de carry-in (de la coloana precedenta) sunt valabili. De asemenea, intarzierea mai depinde si de numarul de biti care trebuiesc adunati. (Figura 3). Adunarea carry-save pune in evidenta faptul ca operatiile de adunare din coloanele separate pot fi facute independent.

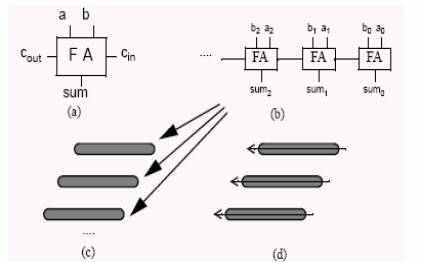
Figura 3. Adunarea produselor partiale. (a) Celula FA. (b) Sumatorul ripple-carry. (c) Se poate folosi tehnica de ripple carry pentru a aduna versiunile shiftate ale deinmultitului. (d) Deoarece sunt n-1 sumatoare ripple carry, fiecare de dimensiune n, aceasta metoda este de complexitate O(n²).

Daca dorim sa adunam 3 vectori de biti, putem utilize FA pentru a aduna cei trei biti de pe o coloana. Rezultatul este un carry-out si un bit de suma la fiecare pozitie, exceptand pozitiile MSB si LSB, care vor avea cate un bit fiecare. Observam ca cei trei vectori de biti au fost "redusi" la doi vectori de biti d.p.d.v al intarzierii date de FA. Utilizand aceasta tehnica, denumita carry-save addition, putem "reduce" un set de vectori care trebuiesc adunati impreuna la 2 vectori de biti. Deoarece FA este elementul de baza al adunarii, FA-urile utilizate in acest context sunt adesea denumite carry-save adders sau CSA's.

Un stil de reducere

Dandu-se setul de produse partiale care trebuiesc adunate folosind CSA, exista cateva moduri de a implementa un sumator care reduce numarul de produse partiale.

Cea mai simpla idee,este numita reducere de produse partiale.

De exemplu, in Figura 4a, se observa PPA-ul generat de o multiplicare de 6-biti cu 6-biti. Putem aduna primii trei vectori de biti utilizand FA, ca in Figura 4b. Rezultatul final se obtine combinand acest rezultat cu restul vectorilor de biti, ca in Figura 4c. Dupa cum se vede, cei trei vectori au for redusi la 2 vectori de biti.

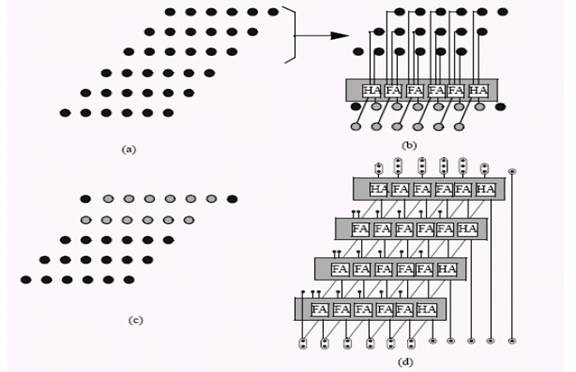
Figura 4. Reducerea produselor partiale - (a) produse partiale initiale (b) utilizarea unui rand de FA pentru a reduce vectorii de 3 biti la 2, utilizand un rand de FA (c) PPA rezultat (d) structura completa.

Observam ca iesirile din primul set de FA pot fi intrari pentru alt rand de FA, pe langa un alt vector de biti. Aceasta structura se repeta pana la obtinerea intregului multiplicator, ca in Figura 4d)..

Caracteristica notabila a arhitecturii acesteia este regularitatea. Aceasta are avantajul ca este foarte usor de realizat layout-ul. Intarzierea acestui bloc este functie de numarul de linii, ceea ce este o imbunatatire substantiala fata de versiunea naiva.

Acesta este principiul folosit de mine pentru descrierea multiplicatorului pe 4 biti.

Schema multiplicatorului Wallace (4 biti):

Am implementat o structura folosind 2 subsisteme, pentru a fi mai usor de urmarit schema. Unul format din 16 porti AND care realizeaza produsele partiale, organizate sub o forma matriciala pentru a fi mai usor de urmarit, si al doilea format din primul plus o serie de Full-Addere si Half-Addere, care formeaza impreuna structura multiplicatorului.

Structura primului subsistem este urmatoarea:

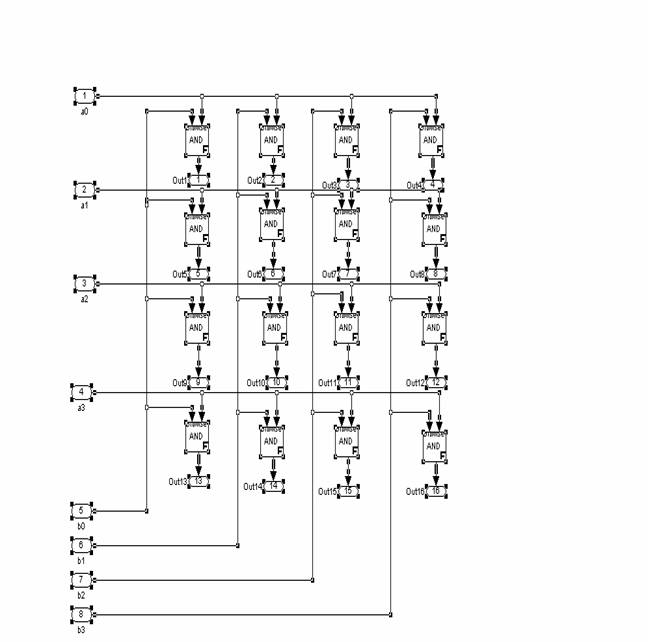
Structura celui de-al doilea subsistem :

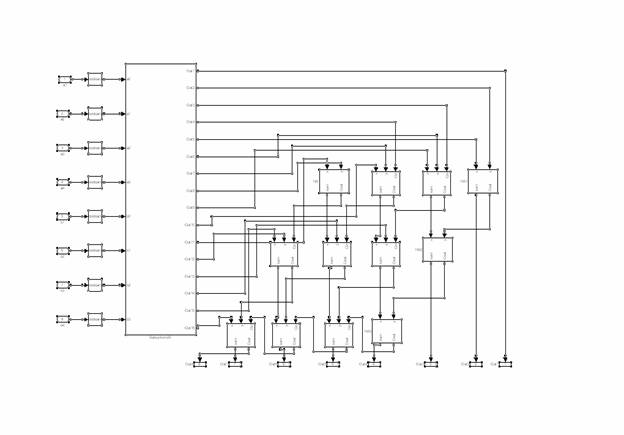
In structura acestui subsistem intra 4 Half-Addere si 8 Full-Addere.

Structura compacta a multiplicatorului este prezentata in figura urmatoare, incluzand si 8 constante pentru verificarea functionarii acestuia :

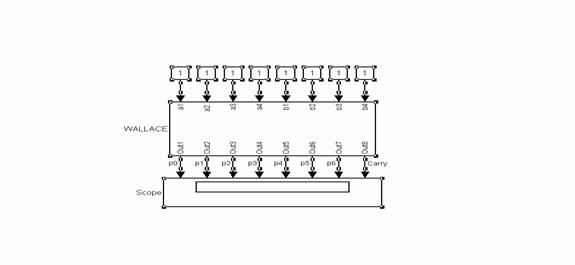
Pentru verificare vom folosi mai multe combinatii de 2 numere.

1. [a4,a3,a2,a1]=1111 (15) 15*15=225 (11100001)

[b4,b3,b2,b1]=1111 (15)

Iata rezultatul in urma simularii 

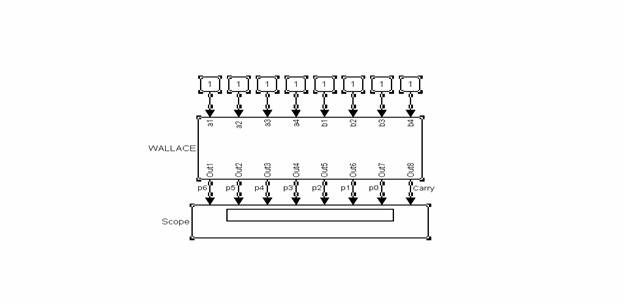
225 (11100001)

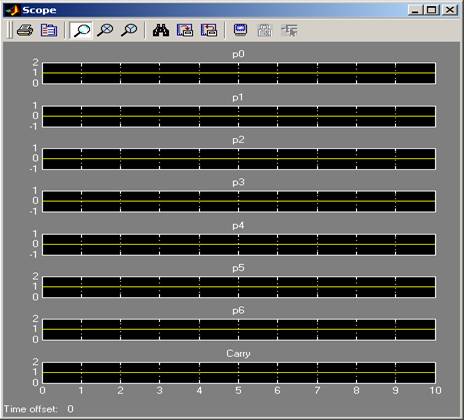
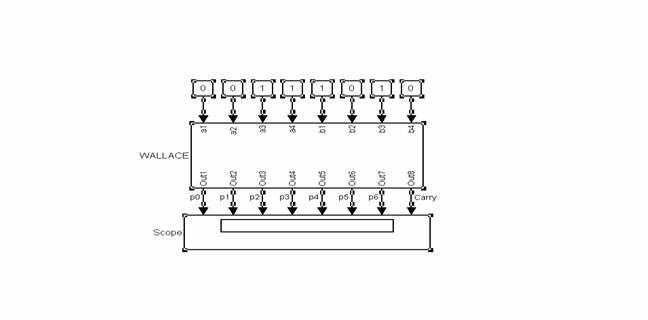
2. [a4,a3,a2,a1]=1100 (12) 12*5=60 (00111100)

[b4,b3,b2,b1]=0101 (5)

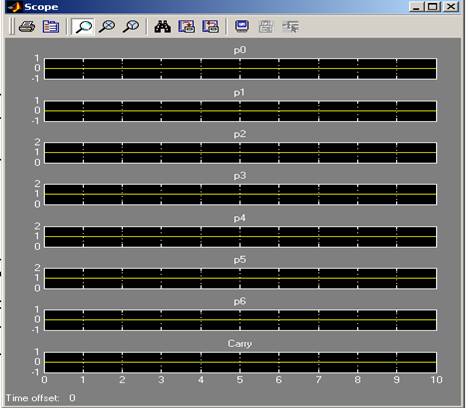
In urma simularii :

60 (00111100)

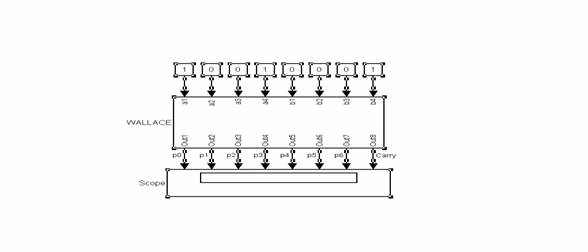
3. [a4,a3,a2,a1]=1001 (9) 9*8=72 (01001000)

[b4,b3,b2,b1]=1000 (8)

In urma simularii :

72 (01001000)

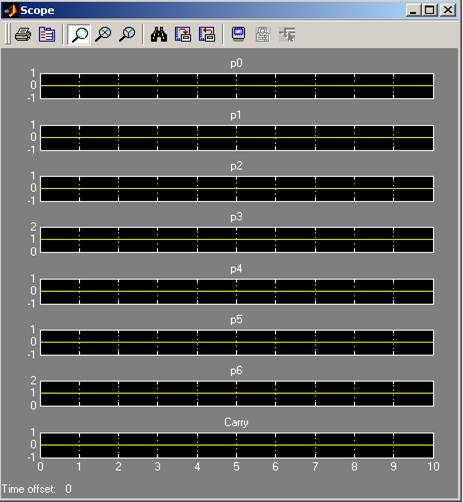
4 . [a4,a3,a2,a1]=1101 (13) 13*11=143 (10001111)

[b4,b3,b2,b1]=1011 (11)

In urma simulaii :

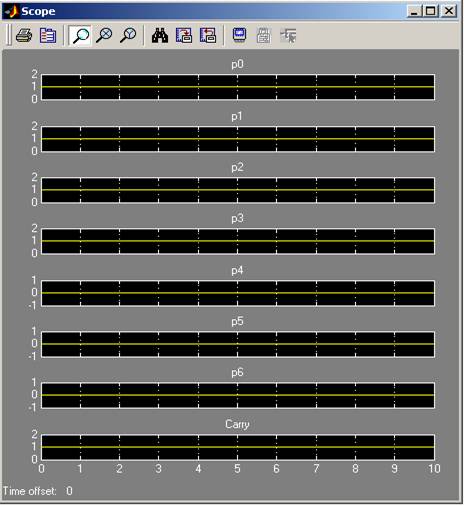
143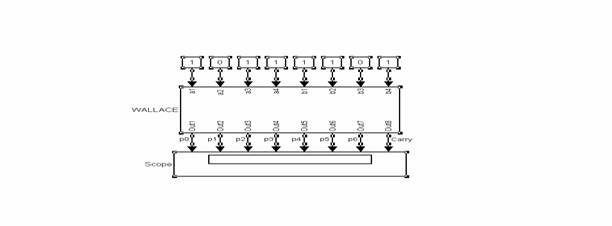

143 (10001111)