SUBPROGRAME

SUBPROGRAME

SUBPROGRAMUL reprezinta parti identificabile prin nume care se pot activa la cerere prin intermediul acetui nume. O parte din subprogram se contruieste ca subprogram daca un algoritm cuprinde in mai multe locuri aceiasi secventa de operatii executabila pentru aceleasi date sau pentru date diferite. In loc ca subprogramul sa cuprinda in acelasi loc, acelasi grup de instructiuni, concepand grupul de intructiuni ca subprogram, el va aparea in program o singura data si se va activa de mai multe ori. Partea respectiva de program rezolva o subproblema din cele in care se descompune problema complexa. In limbajul Pascal, avem doua tipuri de subprograme : procedurile si functiile. Deosebirea intre ele consta in numarul de valori calculate si returnate programului apelat. Procedurile calculeaza mai multe valori sau nici una, iar functiile returneaza o singura valoare asociata numelui functiei. Atat procedurile cat si functiile pot fi standard(predefinite in unitul sistem), cat si nestandard(definite de utilizator). Procedurile si functiile nestandard trebuie declarate obligatoriu inainte de a fi apelate.

O declaratie de subprograme cuprinde:

-un antet de supbrogram care precizeaza interfata subprogramului cu mediul sau, si

blocul subprogramului care descrie functionarea lui interna.

In Pascal subprogramele sunt de 2 tipuri:

-proceduri

-functii.

Procedurile

Procedurile sunt subprograme care pot calcula si returna mai multe valori sau niciuna.

Sintaxa:-intre var si begin principal.

procedure nume_procedura(lista_paramatrii_formali_optional);

begin

end;

Apelul unei proceduri se realizeaza intr-o instructiune procedurala astfel:

nume_procedura(lista_parametrii_efectivi_sau_actuali);

Obs!Listele de parametrii formali si efectivi trebuie sa corespunda ca numar,pozitie,tip.

FUNCTII

O functie calculeaza si returneaza o valoare.

Sintaxa:

function nume_functie(lista,parametrii,formali):tip_rezultat_valoare_returnata;

declaratii_locale(variabile,tipuri locale)

begin

end;

Obs!O functie returneaza o valoare.Tipul rezultatului poate fi unul dintre tipurile simple(toate tipurile numerice:real,char,boolean),iar dintre tipurile structurate doar tipul string.

Obs!Functia returneaza o valoare prin intermediul numelui ei.Din acest motiv una dintre instructiunile functiei trebuie sa fie o instructiune de atribuire cu numele functiei in partea stanga.

Numele functiei nu poate apare deocamdata in partea dreapta a instructiunii(apel recursiv).

Obs!O functie se apeleaza intr-o expresie prin : nume_functie(lista,parametrii,actuali,sau,efectivi);

DOMENIUL DE VIZIBILITATE AL INDENTIFICATORILOR

Prin domeniul de vizibilitate (valabilitate) se intelege zona de program in care e valabila declararea sau definirea unui identificator. Toti indentificatorii definiti sau declarati intr-un bloc sunt cunoscuti in blocul respectiv si se numesc variabile locale. Daca blocul cuprinde blocuri incluse in care identificatorii (variabile locale ale acestora) nu se definesc sau redenumesc, atunci acestea sunt cunoscute in blocurile incluse si se numesc variabile globale pentru acesta. Daca o variabila declarata intr-un bloc se redefineste atunci in blocul in care a fost redeclarata va fi variabila atribuita generata la redeclarare.

DECLARAREA SI APELUL PROCEDURILOR. PARAMETRII FORMALI SI PARAMETRII EFECTIVI

O procedura e un sunbrogram care calculeaza mai multe valori accesibile sau nu programului apelant sau efectueaza anumite operatii fara sa calculeze vreo valoare. Valorile calculate accesibile programului apelant reprezinta parametrii de iesire ai subprogramului. Acestia pot depinde de anumite valori pe care subprogramul le primeste din programul apelant, valori reprezentand parametrii de intrare. Parametrii formali sunt variabile simbolice in care lucreaza subprogramul. Ele sunt declarate in antetul subprogramului si sunt cunoscute numai in interiorul subprogramului. La apelarea procedurii se specifica parametrii efectivi sau actuali prin intermediul instructiunii procedurale. Parametrii efectivi reprezinta variabilele cu care subprogramele lucreaza efectiv in momentul activarii.

Declararea procedurii se face folosind:

PROCEDURE nume_procedura(lista parametrii)

-parametrii precizati la scrierea proedurii sunt parametrii formali si se separa prin ;

-pentru fiecare parametru se precizeaza numele si tipul acestuia.

Apelarea procedurii :

Pentru a executa o procedura aceasta trebuia apelata. La apel se da numele procedurii si valorile concrete ale parametrilor care se separa prin punct si virgula.

Ex : procedure citire(n :integer ; k :char) ;

Begin

..

end;

Cand se apeleaza o procedura, modulul apelant a abandonat temporar, si se executa procedura. In timpul executiei procedurii, parametrii formali sunt inlocuiti in tot corpul procedurii cu parametrii actuali (valori concrete). Dupa executarea procedurii se revine in modulul apelant la linia imediat urmatoare celei care a facut apelul. Parametrii formali si parametrii efectivi nu e obligatoriu sa aiba acelasi nume dar trebuie sa existe o concordanta de numar, tip si ordine.

DECLARAREA SI APELUL FUNCTIILOR

O functie e un subprogram care calculeaza si returneaza programului apelant o singula valoare. Aceasta valoare este asociata numelui functiei. Iar tipul poate fi simplu, string sau reper. Valoarea returnata de functie nu poate avea alt tip structurat decat string.

Declararea unei functii:
FUNCTION nume_functie(lista parametrii formali): identificator de tip;

-nume_functie reprezinta numele functiei, al carei tip este identificator de tip

-identificator de tip = nume de tip simplu: STRING sau REPER;

Blocul functiei trebuie sa contina obligatoriu o instructiune de atribuire prin care identificatorul functiei primeste valoarea unei expresii.

Identificatorul functiei nu are voie sa apara in partea dreapta a unor atribuiri decat daca functia este recursiva.

Apelul unei functii decurge astfel:
- se intrerupe calculul expresiei in care a aparul apelul functiei ;

- se transmit parametrii, daca exista, exact ca la proceduri ;

- se executa functia;

RECURSIVITATE

Prin recursivitate se intelege faptul ca un subprogram se apeleaza pe el insusi, apelul aparand atunci cand subprogramul este inca activ. Exista doua tipuri de recursivitate:

recursivitate directa - cand un subprogram se autoapeleaza in corpul sau ;

recursivitate indirecta - cand avem doua subprograme (x si y), iar x face appel la y si invers ;

Se folosesc algoritmi recursivi atunci cand calculele aferente sunt descrise in forma recursiva.

Recursivitatea este frecvent folosita in prelucrarea structurilor de date definite recursiv. Un subprogram recursiv trebuie scris astfel incat sa respecte regulile :

a) Subprogramul trebuie sa poata fi executat cel putin o data fara a se autoapela ;

b)Subprogramul recursiv se va autoapela intr-un mod in are se tinde spre ajungerea in situatia de executie fara autoapel.

Pentru a permite apelarea recursiva a subprogramelor, limbajul Pascal dispune de mecanime speciale de suspendare a executiei programului apelant, de salvare a informatiei necesare si de reactivare a programului suspendat .

Pentru implementarea recursivitatii se foloseste o zona de memorie in care se poate face salvarea temporala a unor valori. La fiecare appel recursiv al unui subprogram se salveaza in aceasta zona de memorie starea curenta a executiei sale.

Desi variabilele locale ale subprogramului apelant au aceleasi nume cu cele ale subprogramului apelat, orice referire la acesti identificatori se asociaza ultimului set de valori alocate in zona de memorie. Zona de memorie ramane alocata pe tot parcursul executie subprogramului apelat si se dealoca in momentul revenirii in programul apelat. Zona de memorie nu este gestionata explicit de programator ci de catre limbaj.

La terminarea executiei subprogramului apelat recursiv, se reface contextul programului din care s-a facut apelul. Datorita faptului ca la fiecare autoapel se ocupa o zona de memorie, recursivitatea este eficienta numai daca numarul de autoapelari nu este prea mare pentru a nu se ajunge la umplerea zonei de memorie alocata.

Recursivitatea ofera avantajunl unor solutii mai clare pentru probleme si a unei lungimi mai mici a programului. Ea prezinta insa dezavantajul unui timp mai mare de executie si a unui spatiu de memorie alocata ami mare. Este de preferat ca atunci cand programul recursiv poate fi transformat intr-unul iterativ sa se faca apel la cel din urma.

METODA 'DIVIDE ET IMPERA'

NOTIUNI INTRODUCTIVE

Metoda de programare DIVIDE ET IMPERA consta in impartirea problemei initiale de dimensiuni [n] in doua sau mai multe probleme de dimensiuni reduse .In general se executa impartirea in doua subprobleme de dimensiuni aproximativ egale si anume [n/2] . Impartirea in subprobleme are loc pana cand dimensiunea acestora devine suficient de mica pentru a fi rezolvate in mod direct(cazul de baza).Dupa rezolvarea celor doua subprobleme se executa faza de combinare a rezultatelor in vederea rezolvarii intregii probleme .

Metoda DIVIDE ET IMPERA se poate aplica in rezolvarea unei probleme care indeplineste urmatoarele conditii :

se poate descompune in ( doua sau mai multe) suprobleme ;

aceste suprobleme sunt independente una fata de alta (o subproblema nu se rezolva pe baza alteia si nu se foloseste rezultate celeilalte);

aceste subprobleme sunt similare cu problema initiala;

la randul lor subproblemele se pot descompune (daca este necesar) in alte subprobleme mai simple;

aceste subprobleme simple se pot solutiona imediat prin algoritmul simplificat.

Deoarece putine probleme indeplinesc conditiile de mai sus ,aplicarea metodei este destul de rara.

Dupa cum sugereaza si numele 'desparte si stapaneste 'etapele rezolvarii unei probleme (numita problema initiala) in DIVIDE ET IMPERA sunt :

- descompunerea problemei initiale in subprobleme independente ,smilare problemei de baza ,de dimensiuni mai mici ;

descompunerea treptata a subproblemelor in alte subprobleme din ce in ce mai simple ,pana cand se pot rezolva imediata ,prin algoritmul simplificat ;

rezolvarea subproblemelor simple ;

combinarea solutiilor gasite pentru construirea solutiilor subproblemelor de dimensiuni din ce in ce mai mari ;

combinarea ultimelor solutii determina obtinerea solutiei problemei initiale .

Metoda DIVIDE ET IMPERA admite o implementare recursiva ,deorece subproblemele sunt similare problemei initiale, dar de dimensiuni mai mici .

Principiul fundamental al recursivitatii este autoapelarea unui subprogram cand acesta este activ;ceea ce se intampla la un nivel ,se intampla la orice nivel ,avand grija sa asiguram conditia de terminare ale apelurilor repetate .Asemanator se intampla si in cazul metodei DIVITE ET IMPERA ; la un anumit nivel sunt doua posibilitati :

s-a ajuns la o (sub)problema simpla ce admite o rezolvare imediata caz in care se rezolva (sub)problema si se revine din apel (la subproblema anterioara,de dimensiuni mai mari); s-a ajuns la o (sub)problema care nu admite o rezolvare imediata ,caz in care o descompunem in doua sau mai multe subprobleme si pentru fiecare din ele se continua apelurile recursive(ale procedurii sau functiei).

In etapa finala a metodei DIVIDE ET IMPERA se produce combinarea subproblemelor (rezolvate deja) prin secventele de revenire din apelurile recursive.

Etapele metodei DIVIDE ET IMPERA (prezentate anterior)se pot reprezenta prin urmatorul subprogram general (procedura sau functie )recursiv exprimat in limbaj natural:

Subprogram DIVIMP (PROB);

Daca PROBLEMA PROB este simpla

Atunci se rezolva si se obtine solutia SOL

Altfel pentru i=1,k executa DIVIMP(PROB) si se obtine SOL1;

Se combina solutiile SOL 1, ,SOL K si se obtine SOL;

Sfarsit _subprogram;

Deci ,subprogramul DIVIMP se apeleaza pentru problema initiala PROB;aceasta admite descompunerea in K subprobleme simple ;pentru acestea se reapeleaza recursiv subprogramul ;in final se combina solutiile acestor K subprobleme.

De obicei problema initiala se descompune in doua subprobleme mai simple ; in acest caz etapele generale ale metodei DIVIDE ET IMPERA se pot reprezenta concret,in limbaj pseudocod ,printr-o procedura recursiva astfel :

Procedura DIVIMP(li,ls,sol);

Daca ((ls-li)<=eps)

Atunci REZOLVA (li,ls,sol);

Altfel

DIVIDE (li,m,ls);

DIVIMP(li,msol1);

DIVIMP(m,ls,sol2);

COMBINA(sol1,sol2,sol);

Sfarsit_ procedura;

Procedura DIVIMP se apeleaza pentru problema initiala care are dimensiunea intre limita inferioara (li) si limita inferioara(ls);daca (sub)problema este simpla (ls-li<=eps),atunci procedura REZOLVA ii afla solutia imediat si se produce intoarcerea din apelul recursiv;daca (sub)problema este (inca) complexa ,atunci procedura DIVIDE o imparte in doua subprobleme ,alegand pozitia m intre limitele li si ls ;pentru fiecare din cele doua subprobleme se reapeleaza recursiv procedura DIVIMP; in final ,la intoarcerile din apeluri se produce combinarea celor doua soluitii sol1 si sol2 prin apelul procedurii COMBINA.

PROBLEMA TURNURILOR DIN HANOI

Prezentarea algoritmului rezolvarii

Fie trei tije verticale notate A,B,C .Pe tija A se gasesc asezate n discuri de diametre diferite ,in ordinea crescatoare a diametrelor,privind de sus in jos . Initial ,tijele B si C sunt goale .Sa se afiseze toate mutarile prin care discurile de pe tija A se muta pe tija B , in aceeasi ordine ,folosind ca tija de manevra C si resspectand urmatoarele reguli:

la fiecare pas se muta un singur disc;

un disc se poate aseza numai peste un disc cu diametrul mai mare .

Rezolvarea acestei probleme se bazeaza pe urmatoarele considerente logice :

-daca n=1 ,atunci mutarea este immediata AàB(mut discul de pe A pe B); 

daca n=2,atunci sirul mutarilor este : AàC,AàB,CàB;

daca n>2 procedam astfel :

-mut (n-1)discuri AàC;

-mut un disc AàB ;

-mut cele (n-1)discuri CàB.

Observam ca problema initiala se descompune in trei subprobleme mai simple ,similare problemei initiale: mut (n-1)discuri AàC ,mut ultimul disc pe B ,mut cele (n-1)discuri C-->B.Dimensiunile acestor subprobleme sunt : n-1,1,n-1.

Aceste subprobleme sunt independente ,deoarece tijele initial (pe care sunt dispuse discurile ),tijele finale si tijele intermediare sunt diferite.Notam H(n,A,B,C)=sirul mutarilor a n discuri de pe A pe B, folosind C.

PENTRU

n=1 AàB

n>1 H(n,A,B,C)= H(n-1,A,C,B),AB, H(n-1,C,B,A)

program turnurile _hanoi;

var n:byte;

procedure hanoi(n:byte;a,b,c:char);

begin

if n=1 then writeln(a,à,b)

else begin

hanoi(n-1,a,c,b);

writeln(a,à,b);

hanoi(n-1,c,b,a);

end;

end;

begin

write(nr discuri pe tija A =);readln(n);

writeln(mutarile sunt urmatoarele :);

hanoi(n,A,B,C);

readln;readln;

end.

Sortare rapida(quicksort)

Un tablou V se completeaza cu n elemente numere reale .Sa se ordoneze crescator folosind metoda de sortare rapida .

Solutia problemei se bazeaza pe urmatoarele etape implementate in programul principal:

se apeleaza procedura quick cu limita inferioara li=1 si limita superioara ls=n;

functiapoz realizeaza mutarea elementului v[i] exact pe pozitia ce o va ocupa acesta in vectorul final ordonat ; functiapoz intoarce (in k ) pozitia ocupata de acest element;

in acest fel ,vectorul V se imparte in doua parti : li k-1 si k+1ls;

pentru fiecare din aceste parti se reapeleaza proceduraquick,cu limitele modificate corespunzator ;

in acest fel ,primul element din fiecare parte va fi pozitionat exact pe pozitia finala ce o va ocupa in vectorul final ordonat (functiapoz);

fiecare din cele doua parti va fi ,astfel ,inpartita in alte doua parti ;procesul continua pana cand limitele partilor ajung sa se suprapuna ,ceea ce indica ca toate elementele vectorului au fost mutate exact pe pozitiile ce le vor ocupa in vectorul final ;deci vectorul este ordonat ;

in acest moment se produc intoarcerile din apelurile recursive si programul isi termina executia .

program quicksort;

type vector= array [1..50] of real ;

var v:vector;

i,n,k:integer;

function poz(li,ls:integer):integer;

var i,j,modi,modj,m:integer;

man:real;

begin

i:=li; j:=ls;

modi:=0; modj:=-1;

while i<j do

begin

if v[i]>v[j] then

begin

man:=v[i];

v[i]:=v[j];

v[j]:=man;

m:=modi ;

modi:=-modj;

modj:=-m;

end;

i:=i+modi;

j:=j+modj;

end;

poz:=i;

end;

procedure quick(li,ls:integer);

begin

if li<ls then begin

k::=poz(li,ls);

quick(li,k-1);

quick(k+1,ls);

end;

end;

begin

write(cate elemente are vectorul ?=);readln(n);

for i:=1 to n do

begin

write(tastati elementul ,i,=);

readln(v[i]);

end;

quick(1,n);

writeln(vectorul ordonat este :);

for i:=1 to n do writeln(v[i]);

readln;

end.

OBSERVATIE

daca elementul se afla in stanga ,atunci se compara cu elementele din dreapta lui si se sar (j:=j-1)elementele mai mari decat el ;

daca elementul se afla in dreapta ,atunci se compara cu elemente din stanga lui si se sar (i:=i+1)elementele mai mici decat el.

Sortare prin interclasare(mergesort)

Tabloul unidimensional V se completeaza cu n numere reale. Sa se ordoneze crescator folosind sortare prin interclasare.

Sortarea prin interclasare se bazeaza pe urmatoarea logica :

vectorul V se imparte ,prin injumatatiri succesive ,in vectori din ce in ce mai mici ;cand se ating vectorii de maxim doua elemente ,fiecare dintre acestia se ordoneaza printr-o simpla comparare a elementelor ;cate doi astfel de mini- vectori ordonati se interclaseaza succesiv pana se ajunge iar la vectorul V.

program mergesort;

type vector=array[1..50] of real ;

var v:vector ;n,i:word;

procedure schimba(li,ls:word;var a:vector);

var man:real;

begin

if a[li]>a[ls] then begin

man:=a[li];

a[li]:=a[ls];

a[ls]:=man;

end;

end;

procedure interclas(li,m,ls:word;var a:vector);

var b:vector:i,k,p,j:word;

begin

i:=li; j:=m+1; k:=0;

while (i<=m)and(j<=ls) do

begin

inc(k);

if a[i] <a[j] then begin

b[k]:=a[i];

inc(i);

end

else begin

b[k]:=a[j];

inc(j);

end;

end;

if i<=m then for p:=i to m do begin1

inc(k);b[k]:=a[p];

end;

if j<=ls then for p:=j to ls do begin

inc(k) ;b[k]:=a[p];

end;

k:=0;

for p:=li to ls do begin

inc(k);

a[p]:=b[k];

end;

end;

procedure divi(li,ls:word; var a:vector);

var m:word;

begin

if (ls-li)<=1 then schimba(li,ls,a);

else begin

m:=(li+ls)div 2;

divi(li,m,a);

divi(m+1,ls,a);

interclas(li,m,ls,a);

end;

end;

begin

write(cate elemente are vectorul?=);readln(n);

for i:=1 to n do

begin

write(tastati elementul,i,=);

readln(v[i]);

end;

divi(1,n,v);

writeln(vectorul sortat este:);

for i:=1 to n do writeln(v[i]);

end.

OBSERVATII

mecanismul general de tip Divide et Impera se gaseste implementat in procedura divi ;

o astfel de abordare a problemei sortarii unii vector conduce la economie de timp de calcul ,deoarece operatia de interclasare a doi vectori deja ordonati este foarte rapida ,iar ordonarea independenta celor doua jumatati(mini- vectori) consuma in total aproximativ a doua parte din timpul care ar fi necesar ordonarii vectorului luat ca intreg .

Sortare prin insertie binara

Sa se ordoneze crescator un tablou unidimensional V de n numere reale ,folosind sortarea prin insertie binara .

Pentru fiecare element v[i] se procedeaza in patru pasi:

se considera ordonate elementele v[1],v[2],.,v[i-1];

se cauta pozitia k pe care urmeaza s-o ocupe v[i] intre elementele v[1],v[2],,v[i-1](procedura poz prin cautare binara);

se deplaseaza spre dreapta elementele din pozitiile k,k+1,,n(procedura deplasare);

insereaza elementul v[i] in pozitia k (proceduradeplasare);

se obtine o succesiune de k+1 elemente ordonate crescator.

program sortare _binara;

type vector =array[1..50] of real ;

var n,k,i:integer;

v:vector;

function poz(li,ls,i:integer):integer;

var m:integer;

begin

if li=ls then

if v[i]<v[j] then poz:=li

else poz:=i

else if ls-li=1 then if v[i]<v[ls] then if v[i]>=v[li]

then poz:=ls

else poz:=li

else poz:=i

else begin

m:=(li+ls)div 2;

if v[i]<v[m] then poz:=poz(li,m,i)

else poz :=poz(m,ls,i);

end;

end;

procedure deplasare(k,i:integer);

var man:real;

j:integer;

begin

if k<i then begin

man:=v[i];

for j:=I downto k+1 do v[j]:=v[j-1];

v[k]:=man;

end;

end;

begin

write(cate elemente are vectorul?=);readln(n);

for i:=1 to n do begin

write(tastati elementul ,i,=);readln(v[i]);

end;

for i:=2 to n do begin

k:=poz(1,i-1,i);

deplasare(k,i);

end;

writeln(vectorul ordonat este :);

for i:=1 to n do writeln(v[i]);

readln;

end.

CONCLUZII

(analiza a complexitatii timp pentru algoritmii Divide et Impera)

Algoritmii de tip Divide et Impera au buna comportare in timp ,daca se indeplinesc urmatoarele conditii:

dimensiunile subprogramelor(in care se imparte problema initiala )sunt aproximativ egale(principiul balansarii);

lipsesc fazele de combinare a solutiilor subproblemelor(cautare binara).

Metoda BACKTRACKING

La dispozitia celor care rezolva probleme cu ajutorul calculatorului exista mai multe metode . Dintre acestea cel mai des utilizate sunt:

metoda Greedy;

metoda Divide et impera;

metoda Branch and Bound;

metoda Backtracking;

Metoda Backtracking se aplica problemelor in care solutia poate fi reprezentata sub forma unui vector x = (x1, x2, x3, xk, xn) S, unde S este multimea solutiilor problemei si S = S1 x S2 x x Sn, si Si sunt multimi finite avand s elemente si xi si , (¥)i = 1..n.

Pentru fiecare problema se dau relatii intre componentele vectorului x, care sunt numite conditii interne; solutiile posibile care satisfac conditiile interne se numesc solutii rezultat. Metoda de generare a tuturor solutiilor posibile si apoi de determinare a solutiilor rezultat prin verificarea indeplinirii conditiilor interne necesita foarte mult timp.

Metoda backtracking evita aceasta generare si este mai eficienta. Elementele vectorului x, primesc pe rand valori in ordinea crescatoare a indicilor, x[k] va primi o valoare numai daca au fost atribuite valori elementelor x1.. x[k-1]. La atribuirea valorii lui x[k] se verifica indeplinirea unor conditii de continuare referitoare la x1x[k-1]. Daca aceste conditii nu sunt indeplinite, la pasul k, acest lucru inseamna ca orice valori i-am atribui lui x[k+1], x[k+1], .. x[n] nu se va ajunge la o solutie rezultat.

Metoda backtracking construieste un vector solutie in mod progresiv incepand cu prima componenta a vectorului si mergand spre ultima cu eventuale reveniri asupra atribuirilor anterioare.

Metoda se aplica astfel :

se alege prima valoare sin S1 si I se atribuie lui x1 ;

se presupun generate elementele x1x[k-1], cu valori din S1..S[k-1]; pentru generarea lui x[k] se alege primul element din S[k] disponibil si pentru valoarea aleasa se testeaza indeplinirea conditiilor de continuare.

Pot aparea urmatoarele situatii :

a) x[k] indeplineste conditiile de continuare. Daca s-a ajuns la solutia finala (k = n) atunci se afiseaza solutia obtinuta. Daca nu s-a ajuns la solutia finala se trece la generarea elementului urmator x [k-1];

b) x[k] nu indeplineste conditiile de continuare. Se incearca urmatoarea valoare disponibila din S[k]. Daca nu se gaseste nici o valoare in S[k] care sa indeplineasca conditiile de continuare, se revine la elementul x[k-1] si se reia algoritmul pentru o noua valoare a acestuia. Algoritmul se incheie cand au fost luate in considerare toate elementele lui S1.

Este o tehnica de programare aplicabila algoritmilor care ofera mai multe solutii si are ca rezultat obtinerea tuturor solutiilor problemei. Fiecare solutie se memoreaza intr-o structura de date de tip stiva implementata cu ajutorul unui vector. Deci fiecare solutie poate fi pusa sub forma unui vector.

Intr-un algoritm backtracking ne intereseaza toate solutiile posibile. Pentru a obtine fiecare solutie finala se completeaza stiva nivel cu nivel trecand astfel prin niste solutii partiale. Astfel solutiile finale cat si cele partiale pentru a fi luate in considerare trebuie sa indeplineasca anumite conditii numite conditii de validare. O solutie care indeplineste o astfel de conditie se numeste solutie valida.

Toate configuratiile stivei ce reprezinta solutii finale sunt alcatuite din elementele aceleiasi multimi bine definite pe care o numim multimea solutiilor. Fiecare noua solutie partiala se obtine prin completarea solutiei partiale precedente cu inca o nivel pe stiva. La fiecare nivel se pun valori din multimea solutiilor care nu au fost incercate pana cand se obtine o solutie valida. In acest moment se trece la nivelul urmator in stiva pentru a completa mai departe solutia reluand incercarile pe noul nivel.

La un moment dat pe un anumit nivel nu mai exista nici o valoare neincercata din multimea valorilor problemei. In acest caz se face un pas inapoi in stiva la nivelul anterior si se reia cautarea cu valorile ramase neincercate pe acest nivel anterior.

Respectivul nivel a mai fost vizitat dar l-am abandonat dupa ce am pus o valoare care a generat o solutie valida. Deci este posibil sa fi ramas aici valori neincercate. Daca nici pe acest nivel nu mai avem valori neincercate mai facem un pas inapoi in stiva. Mecanismul revenirilor a determinat denumirea de metoda backtracking.

Plecand de la nivelul 1 si repetand algoritmul pana cand pe toate nivelele au fost incercate toate valorile din multimea valorilor se obtin solutii finale care se tiparesc.

Vom implementa metoda backtracking iterativ folosind o rutina unica aplicabila oricarei probleme. Rutina va apela proceduri si functii care au intotdeauna acelasi nume si parametri si care din punct de vedere al metodei realizeaza acelasi lucru.

Sarcina rezolvatorului este sa scrie explicit - pentru fiecare problema - procedurile si functiile aplicate pe rutina. Astfel gasirea urmatorului element netestat de pe un nivel k al stivei St se face cu procedura succesor (as,St,k)

Odata ales un element testarea conditiilor de validare se face cu procedura valid (ev,St,k).

Testul daca s-a ajuns sau nu la o solutie finala se face cu functia solutie (k)

Solutia se tipareste cu procedura tipar.

De asemenea fiecare nivel al stivei trebuie initializat cu o valoare aflata inaintea tuturor valorilor posibile din multimea solutiilor. Aceasta afisare se face cu procedura init (k,St).

Rutina Backtracking

K:=1; init (1,St);

while k>0 do

begin

repeat

succesor (as,St,k);

if as then valid (ev,St,k);

until (not as) or (as and ev);

if as then

if solutie (k) then tipar

else begin

k:=k+1;

init(k,St);

end;

else k:=k-1;

end;

end;

PROGRAME SI PROBLEME

Turnuri de cuburi

Se dau n cuburi numerotate 1,2,,n, de laturi Li si culori Ci, i=1,2,,n (fiecare culoare este codificata printr-un caracter). Sa se afiseze toate turnurile care se pot forma luand k cuburi din cele n disponibile, astfel incat:

-laturile cuburilor din turn sa fie in ordine crescatoare;

-culorile a oricare doua cuburi alaturate din turn sa fie diferite.

program cuburi;

type stiva=array [1..100] of integer;

var st:stiva;

i,n,p,k:integer;

as,ev:boolean;

L:array [1..10] of integer;

C:array [1..10] of char;

procedure init(k:integer;var st:stiva);

begin

st[k]:=0;

end;

procedure succesor(var as:boolean;var st:stiva;k:integer);

begin

if st[k]<n then

begin

st[k]:=st[k]+1;

as:=true;

end

else as:=false;

end;

procedure valid(var ev:boolean;st:stiva;k:integer);

var i:integer;

begin

ev:=true;

for i:=1 to k-1 do if L[st[k]]<=L[st[i]] then ev:=false;

if C[st[k]]=C[st[k-1]] then ev:=false;

end;

function solutie(k:integer):boolean;

begin

solutie:=(k=p);

end;

procedure tipar;

var i:integer;

begin

for i:=1 to p do write(st[i],' ');

writeln;

end;

begin

write('n= ');read(n);

write('p= ');read(p);

for i:=1 to n do

begin

write('L[',i,']=');readln(L[i]);

write('C[',i,']=');readln(C[i]);

end;

k:=1;init(k,st);

while k>0 do

begin

repeat

succesor(as,st,k);

if as then valid(ev,st,k);

until (not as) or (as and ev);

if as then if solutie(k) then tipar

else begin

k:=k+1;

init(k,st);

end

else k:=k-1;

end;

end.

Dintr-un nr. de 6 cursuri optionale un elev trebuie sa aleaga 3. Sa se afiseze toate posibilitatile de alegere precum si nr. lor.

program cursuri;

const n=6;

p=3;

type stiva=array [1..10] of integer;

var st:stiva;

ev,as:boolean;

k:integer;

procedure init(k:integer;var st:stiva);

begin

if k>1 then st[k]:=st[k-1]

else if k=1 then st[k]:=0;

end;

procedure succesor(var as:boolean;var st:stiva;k:integer);

begin

if st[k]<n-p+k then begin st[k]:=st[k]+1;

as:=true;

end

else as:=false;

end;

procedure valid(var ev:boolean;var st:stiva;k:integer);

var i:integer;

begin

ev:=true;

for i:=1 to k-1 do if st[i]=st[k] then ev:=false;

end;

function solutie(k:integer):boolean;

begin

solutie:=(k=p);

end;

procedure tipar;

var i:integer;

begin

for i:=1 to p do write (st[i]);

writeln;

end;

begin;

k:=1;init(k,st);

while k>0 do

begin

repeat

succesor (as,st,k);

if as then valid(ev,st,k);

until (not as) or (as and ev);

if as then

if solutie(k) then tipar

else begin

k:=k+1;

init(k,st)

end

else k:=k-1;

end;

readln;

end.

Numerele care ii plac lui Irinel

Lui IRINEL ii plac nr. formate numai din cifre pare cifre aflate in ordin_______escatoare. Sa se determine si sa se afiseze pe ecran toate nr. de n cifre (0<n<10) care ii plac lui Gigel. Valoarea lui n este un nr. natural care se citeste de la tastatura.

program nr_lui_IRINEL;

type stiva=array[1..100] of integer;

var st:stiva;

i,n,k:integer;

as,ev:boolean;

procedure init(k:integer;var st:stiva);

begin

st[k]:=-1;

end;

procedure succesor(var as:boolean;var st:stiva;k:integer);

begin

if st[k]<9 then begin st[k]:=st[k]+1;

as:=true;

end

else as:=false;

end;

procedure valid(var ev:boolean;st:stiva;k:integer);

var i:integer;

begin

ev:=true;

for i:=1 to k-1 do

if st[i] mod 2 <> 0 then ev:=false;

for i:=1 to k-1 do

if st[i]<st[i+1] then ev:=false;

end;

function solutie(k:integer):boolean;

begin

solutie:=(k=n);

end;

procedure tipar;

var i:integer;

begin

for i:=1 to n do write(st[i]);

writeln;

end;

begin

write('n= ');readln(n);

k:=1 ;init(k,st);

while k>0 do

begin

repeat

succesor(as,st,k);

if as then valid(ev,st,k);

until (not as) or (as and ev);

if as then if solutie(k) then tipar

else begin

k:=k+1;

init(k,st);

end

else k:=k-1;

end;

readln;

end.

PROGRAM COMISV

program comisv;

type stiva=array[1..100] of integer;

var st:stiva;

i,j,n,k:integer;

as,ev:boolean;

a:array[1..20,1..20] of integer;

procedure init(k:integer;var st:stiva);

begin

st[k]:=1;

end;

procedure succesor(var as:boolean;var st:stiva;k:integer);

begin

if st[k]<n then begin

st[k]:=st[k]+1;

as:=true

end

else as:=false

end;

procedure valid(var ev:boolean;st:stiva;k:integer);

var i:integer;

begin

ev:=true;

if a[st[k-1],st[k]]=0 then ev:=false

else

for i:=1 to k-1 do if st[i]=st[k] then ev:=false;

if (k=n) and (a[1,st[k]]=0) then ev:=false

end;

function solutie(k:integer):boolean;

begin

solutie:=(k=n)

end;

procedure tipar;

var i:integer;

begin

for i:=1 to n do

write('nodul=',st[i]);

writeln('------');

end;

begin

write('nr. de noduri=');readln(n);

for i:= 1 to n do

for j:=1 to i-1 do begin

write('a[',i,',',j,']='); readln(a[i,j]);

a[j,i]:=a[j,i];

end;

end;

st[1]:=1; k:=2;

init(k,st);

while k>0 do

begin

repeat

succesor(as,st,k);

if as then valid(ev,st,k);

until (not as) or (as and ev);

if as then if solutie(k) then tipar

else begin

k:=k+1;

init(k,st);

end

else k:=k-1;

end;

end.

PROGRAM DAME

program dame;

type stiva=array[1..100] of integer;

var st:stiva;

n,k:integer;

as,ev:boolean;

procedure init(k:integer;var st:stiva);

begin

st[k]:=0;

end;

procedure succesor(var as:boolean;var st:stiva;k:integer);

begin

if st[k]<n then begin st[k]:=st[k]+1;

as:=true end

else as:=false;

end;

procedure valid(var ev:boolean;var st:stiva;k:integer);

var i:integer;

begin

ev:=true;

for i:=1 to k-1 do if (st[k]=st[i]) or (abs(st[k]-st[i])=abs(k-i)) then ev:=false;

end;

function solutie(k:integer):boolean;

begin

solutie:=(k=n);

end;

procedure tipar;

var i:integer;

begin

for i:=1 to n do write(st[i]);

writeln;

end;

begin

write('n:');readln(n);

k:=1;init(k,st);

while k>0 do

begin

repeat

succesor(as,st,k);

if as then valid(ev,st,k);

until (not as) or (as and ev);

if as then if solutie(k) then tipar

else begin

k:=k+1;

init(k,st); end

else k:=k-1;

end;

readln;

end.

PROGRAM DESC 2

program desc2;

type stiva=array[1..100] of integer;

var st:stiva;

s,n,k:integer;

as,ev:boolean;

procedure init(k:integer;var st:stiva);

begin

st[k]:=0;

end;

procedure succesor(var as:boolean;var st:stiva;k:integer);

begin

if st[k]<n then begin

st[k]:=st[k]+1;

as:=true;

end

else as:=false;

end;

procedure valid(var ev:boolean;st:stiva;k:integer);

var i:integer;

begin

s:=0;

ev:=true;

for i:=1 to k do s:=s+st[i];

if s<=n then ev:=true

else ev:=false;

end;

function solutie(k:integer):boolean;

begin

solutie:=(s=n);

end;

procedure tipar;

var i:integer;

begin

for i:=1 to k do write(st[i]);

writeln;

end;

begin

write('n=');readln(n);

while k>0 do

begin

repeat

succesor(as,st,k);

if as then valid(ev,st,k);

until (not as) or (as and ev);

if as then if solutie(k) then tipar

else begin

k:=k+1;

init(k,st);

end

else k:=k-1;

end;

end.

PROGRAM PARANTEZE

program paranteze;

type stiva=array[1..100] of integer;

var st:stiva;

npd,npi,n,k:integer;

as,ev:boolean;

procedure init(k:integer;var st:stiva);

begin

st[k]:=0;

end;

procedure succesor(var as:boolean;var st:stiva;k:integer);

begin

if st[k]<2 then

begin

st[k]:=st[k]+1;

as:=true;

end

else as:=false;

end;

procedure valid(var ev:boolean;st:stiva;k:integer);

var i:integer;

begin

npd:=0;

npi:=0;

for i:=1 to k do

if st[i]=1 then npd:=npd+1

else npi:=npi+1;

if (npd>=npi) and (npd<=n div 2) then ev:=true

else ev:=false;

end;

function solutie(k:integer):boolean;

begin

solutie:=(k=n);

end;

procedure tipar;

var i:integer;

begin

if npd=npi then

for I:=1 to k do

if st[i]=1 then write('(')

else write(')');

writeln;

begin

write('n= ');read(n);

st[1]=1;

k:=1;init(k,st);

while k>0 do

begin

repeat

succesor (as,st,k);

if as then valid(ev,st,k);

until (not as) or (as and ev);

if as then

if solutie(k) then tipar

else begin

k:=k+1;

init(k,st)

end

else k:=k-1;

end;

readln;

end.

PROGRAM PARTITI ALE UNUI NUMAR

program partitii_ale_unui_nr;

type stiva=array [1..10] of integer;

var st:stiva;

ev,as:boolean;

n,k:integer;

procedure init(k:integer;var st:stiva);

begin st[k]:=0;

end;

procedure succesor(var as:boolean;var st:stiva;k:integer);

begin if st[k]<n then begin st[k]:=st[k]+1;

as:=true;

end

else as:=false;

end;

procedure valid(var ev:boolean;var st:stiva;k:integer);

var i,s:integer;

begin s:=0;

for i:=1 to k do

s:=s+st[i];

if s<=n then ev:=true

else ev:=false;

end;

function solutie(k:integer):boolean;

begin

solutie:=(k=n);

end;

procedure tipar;

var i:integer;

begin

for i:=1 to n do write (st[i]);

writeln;

end;

begin;

write ('n:=');readln (n);

k:=1;init(k,st);

while k>0 do

begin

repeat

succesor (as,st,k);

if as then valid(ev,st,k);

until (not as) or (as and ev);

if as then

if solutie(k) then tipar

else begin

k:=k+1;

init(k,st)

end

else k:=k-1;

end;

readln;

end.

PROGRAM PCARTEZ

program pcartez;

type stiva=array[1..100] of integer;

var st:stiva;

i,n,k:integer;

as,ev:boolean;

a:array [1..100] of integer;

procedure init(k:integer;var st:stiva);

begin

st[k]:=0;

end;

procedure succesor(var as:boolean;var st:stiva;k:integer);

begin

if st[k]<a[k] then begin

st[k]:=st[k]+1;

as:=true;

end

else as:=false;

end;

procedure valid(var ev:boolean;st:stiva;k:integer);

var i:integer;

begin

ev:=true;

end;

function solutie(k:integer):boolean;

begin

solutie:=(k=n);

end;

procedure tipar;

var i:integer;

begin

for i:=1 to n do write(st[i]);

writeln;

end;

begin

write('Numarul de multimi= ');readln(n);

for i:=1 to n do begin

write('a[',i,']=');readln(a[i]);

end;

k:=1;init(k,st);

while k>0 do

begin

repeat

succesor(as,st,k);

if as then valid(ev,st,k);

until (not as) or (as and ev);

if as then if solutie(k) then tipar

else begin

k:=k+1;

init(k,st);

end

else k:=k-1;

end;

end.

PROGRAM SIR

program sir;

type stiva=array[1..100] of integer;

vector=array[1..100] of integer;

var st:stiva;

n,k,i:integer;

as,ev:boolean;

a:vector;

procedure init(k:integer;var st:stiva);

begin

st[k]:=0;end;

procedure succesor(var as:boolean;var st:stiva;k:integer);

begin

if st[k]<n then begin

st[k]:=st[k]+1;

as:=true;

end

else as:=false;

end;

procedure valid(var ev:boolean;st:stiva;k:integer);

var i:integer;

begin

ev:=true;

for i:=1 to k-1 do if st[k]=st[i] then ev:=false;

if (a[st[k]]<0) and (a[st[k-1]]<0) then ev:=false;

end;

function solutie(k:integer):boolean;

begin

solutie:=(k=n);

end;

procedure tipar;

var i:integer;

begin

for i:=1 to n do write(a[st[i]],' ');

writeln;

end;

begin

write('n=');readln(n);

for i:=1 to n do

begin

write('a[',i,']=');readln(a[i]);

end;

k:=1;init(k,st);

while k>0 do

begin

repeat

succesor(as,st,k);

if as then valid(ev,st,k);

until (not as) or (as and ev);

if as then if solutie(k) then tipar

else begin

k:=k+1;

init(k,st);

end

else k:=k-1;

end;

end.

PROGRAM SORTARE

program sort;

type vector=array[1..10] of integer;

var a:vector;

n,i:integer;

procedure sort(p,q:integer;var a:vector);

var m:integer;

begin

if a[p]>a[q] then

begin

m:=a[p];

a[p]:=a[q];

a[q]:=m

end;

end;

procedure interc(p,q,m:integer;var a:vector);

var b:vector;

i,j,k:integer;

begin

i:=p;

j:=m+1;

k:=1;

while (i<=m) and (j<=q) do

if a[i]<=a[j] then

begin

b[k]:=a[i];

i:=i+1;

k:=k+1

end

else begin

b[k]:=a[j];j:=j+1;k:=k+1

end;

if i<=m then

for j:=i to m do begin

b[k]:=a[j];

k:=k+1;

end

else

for i:=j to q do begin

b[k]:=a[j];

k:=k+1;

end;

k:=1;

for i:=p to q do begin

a[i]:=b[k];

k:=k+1;

end

end;

procedure divimp(p,q:integer; var a:vector);

var m:integer;

begin

if (q-p)<=1 then sort(p,q,a)

else begin

m:=(p+q) div 2;

divimp(p,m,a);

divimp(m+1,q,a);

interc(p.q.m.a);

end

end;

write('n= ');read(n);

for i:=1 to n do

begin

write('a[',i,']=');readln(a[i]);

end;

divimp(1,n,a);

for i:=1 to n do

writeln(a[i]);

end.

program p2;

var a,b,c:char;

n:integer;

procedure hanoi(n:integer;a,b,c:char);

begin

if n=1 then writeln(a,b)

else begin

hanoi(n-1,a,c,b);

writeln(a,b);

hanoi(n-1,c,b,a);

end;

end;

begin

write('n=');readln(n);

a:='a';b:='b';c:='c';

hanoi(n,a,b,c);

readln;

end.

Sortare rapida (QuickSort)

Secventa de comparatie din metoda lui Batcher este predeterminata; de fiecare data se compara aceleasi perechi de chei, indiferent de rezultatele comparatiilor anterioare.

Sortarea rapida, in schimb, foloseste rezultatele fiecarei comparatii pentru a stabilii care sunt cheile care urmeaza a fi comparate.

Deci, se foloseste urmatoare schema: se utilizeaza doi indicatori i si j, cu i=1 si j=N. Se compara Ki cu Kj si daca nu este necesar interschimbul, se micsoreaza j cu 1, repetandu-se procesul. Daca apare un interschimb, se mareste i cu 1si se continua compararea marind i pana la aparitia unui interschimb. Apoi, se micsoreaza din nou j, continuandu-se in acelasi mod, pana cand i=j.

Exemplu:

Fiecare comparatie din exemplu, a implicat cheia 503; in general, fiecare comparatie va implica valoarea originala a cheii K1, deoarece ea va fi modificata odata cu fiecare schimbare de directie.In momentul cand i=j, inregistrarea originala R1, va fi plasata in pozitia finala, deoarece se poate vedea ca nu vor exista chei mai mari la stanga sa si nici mai mici la dreapta sa. Inregistrarile vor fi impartite intr-o asemenea maniera, incat problema initiala este redusa la doua probleme mai simple: sortarea Ri - Ri-1 si sortarea Ri+1 - RN. Se poate aplica aceasi tehnica fiecarei dintre aceste doua multimi de inregistrari.

Pentru a tine minte multimile de elemente care sunt impartite, se foloseste o stiva. Alt exemplu, care arata modul in care sunt sortate inregistrarile prin acesta metoda, este dat in tabelul de mai jos. Parantezele, indica inregistrarile care mai trebui sortate; inregistrarile impartite in grupe sunt reprezentate prin doua variabile l si r, care reprezinta limitele inregistrarilor care sunt curent examinate.

 Aceata metoda de sortare, a fost numita sortare prin interschimb de partitii; ea a fost propusa de C. A. R. Hoare. Hoare, si-a denumit metoda 'sortare rapida'. Intregul proces de sortare, necesita doar 48 de comparatii, fiind intrecuta la numarul de comparatii doar de sortarea prin insertie binara, care are un numar de 47 de comparatii. Si numarul de interschimbari este destul de mic, ea necesitand doar 17 interschimbari.

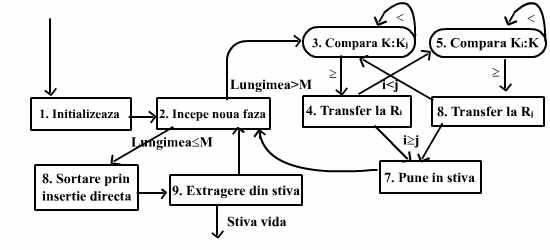
Algoritmul:

Inregistrarile R1, , RN sunt rearanjate pe loc; dupa terminarea sortarii, cheile lor vor fi in ordine K1, , KN. Pentru memorarea temporara, este necesara o stiva cu cel mult log2N intrari.

1. Se presupune prezenta cheilor artificiale K0=- si KN+1=+, astfel incat, K0KiKN+1 pentru 1iN. (egalitatea este permisa).
2. Subgrupele de inregistrari ale lui M, sau un numar redus de inregistrari, sunt sortate prin insertie directa, unde M1 este un parametru care trebuie ales dupa cum se descrie mai jos.
3. Pe durata unei etape particulare, sunt efectuate una sau doua comparatii suplimentare (permitand indicatorilor i si j sa se intersecteze).
4. Inregistrarile cu chei egale, sunt interschimbate, desi nu este strict necesar (Idea este datorata lui R. C. Singleton, si ajuta la sectionarea grupurilor de inregistrari pe jumatate, atunci cand sunt un numar egal de elemente).

1. [Initializeaza.] Stabileste stiva vida si l=1, r=N
2. [Incepe o noua etapa.] (Se doreste sortarea grupurilor de inregistrari Rl Rr). Daca r-1<M, mergi la pasul 8. In caz contrar, stabileste i=l, j=r, K=Kl, R=Rl.
3. [Compara K:Kj.]Daca K<Kj, micsoreaza j cu 1 si repeta acest pas.
4. [Transfer la Ri.] (La acest pas, Ki este o cheie nesemnificativa K, si KKj.) Daca ji, stabileste Ri=R si mergi la pasul 7. Altfel, Ri=Rj mareste i cu 1.
5. [Compara Ki:K.] Daca Ki<K, mareste i cu 1 si repeta acest pas.
6. [Transfer la Rj.] (La acest pas, Kj este o cheie nesemnificativa K, siKKi). Daca ji, stabileste Rj=R si i=j. Altfel, Rj=Ri, micsoreaza j cu 1 si mergi la pasul 3.
7. [Pune in stiva.] (Acum, grupa de inregistrari, RlRiRr a fost partitionata astfel incat KkKi pentru lki si KiKk pentru ikr.) Daca r-ii-l, plaseaza (i+1,r) in varful stivei si stabileste r=i-1. In caz contrar, plaseaza (l,i-1) in varful stivei si stabileste l=i+1. (Fiecare intrare (a,b) in stiva, reprezinta o cerere de sortare a grupului de inregistrari RaRb la un anumit timp, in viitor). Acum, mergi inapoi la pasul 2.
8. [Sortare prin insertie directa.] pentru j=l+1 la r-1, efectueaza urmatoarele operatii: stabileste K=Kj, R=Rj, i=j-1; apoi, stabileste Ri+1=Ri, i=i-1, de zero sau mai multe ori, pana cand Ki=K; apoi stabileste Ri+1=R. (Acesta, este in esenta algoritmul de sortare prin insertie directa, aplicat grupului de inregistrari formate din M sau mai putine elemente.)
9. [Anuleaza stiva.] Daca stiva este vida, sortarea s-a efectuat; in caz contrar, inlatura intrarea ei din varf (l',r'), stabileste l=l', r=r' si revino la pasul 2.

Algoritmul reprezentat prin scheme logice: