| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Datorita tensiunii superficiale, suprafata libera a unui lichid în echilibru, aflat în contact cu alte medii, ia o forma curba, numita menisc. La suprafata de contact solid – lichid apar de asemeni forte de atractie moleculara, denumite forte de adeziune în timp ce fortele ce actioneaza între molecule mai sunt denumite si forte de coeziune. În functie de raportul intensitatii acestor doua forte, apar doua cazuri diferite, reflectate în forma stratului superficial la suprafata de separatie dintre lichid si solid. Parametrul care caracterizeaza meniscul este unghiul format de tangenta la suprafata lichidului cu suprafata solida cu care este în contact, numit unghi de udare sau unghi de racordare.
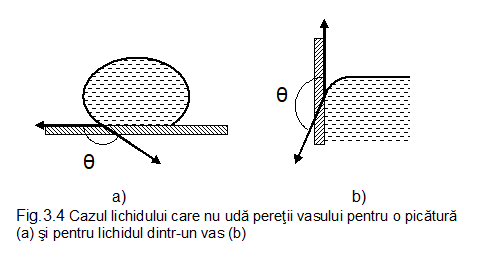
a. Cazul în care fortele de coeziune sunt mai mari decât fortele de adeziune. În acest caz, suprafata de contact dintre lichid si solid are tendinta de micsorare, iar unghiul de udare este mai mare decât π/2 (Fig.3.4).
Se spune despre lichidele care sunt în aceasta situatie ca nu uda peretii vasului, iar suprafata lichidului in apropierea vasului (meniscul) este concava.
b. Cazul în care fortele de coeziune sunt mai mici decât fortele de adeziune. În acest caz, unghiul de udare este mai mic decât π/2 (Fig.3.5). Se spune despre lichidele care sunt în aceasta situatie ca uda peretii vasului, iar suprafata lichidului in apropierea vasului (meniscul) este convexa.
Trebuie precizat ca aceasta comportare a suprafetei libere a lichidului la suprafata de contact cu solidul depinde (într-o mica masura) si de natura gazului aflat în contact cu lichidul. Un alt parametru care influenteaza forma meniscului este puritatea celor trei medii aflate în contact.

Existenta
meniscului determina aparitia unei presiuni suplimentare Δp, fata de cea
exercitata de suprafata plana a lichidului. Expresia
matematica a presiunii suplimentare a fost obtinuta de Laplace
(1807). Pentru o suprafata sferica se poate scrie:
![]() 1(3.9)
1(3.9)
iar pentru o suprafata cilindrica:
![]() 2 (3.10)
2 (3.10)
Aceasta suprapresiune este importanta în cazul picaturilor de lichid în aer sau invers, al picaturilor de aer în lichid. Sub actiunea fortelor de tensiune superficiala, picaturile iau forma sferica, datorita conditiei fizice de atingere a unui minim al energiei potentiale (3.2). Pentru un volum dat, forma sferica are suprafata cea mai mica si de aceea si forma picaturilor este sferica. Daca pentru picaturile de aer în lichid nu mai apar alte probleme, picaturile de lichid sunt supuse si actiunii greutatii proprii, astfel încât, o data cu cresterea în dimensiune, forma picaturii se departeaza tot mai mult de sfera, ea aplatizându-se. Dupa cum se poate vedea din relatia (3.9), suprapresiunea data de fortele superficiale este invers proportionala cu raza bulei, ea fiind cu atât mai importanta cu cât raza este mai mica. Folosind datele din tabelul 3.1. într-o bula de aer cu raza de un micron, aflata în apa presiunea atinge o valoare de 1.46x105 N/m2, adica mai mare decât presiunea atmosferica.
Fenomenele capilare sunt determinate de fortele de interactiune dintre un lichid si un corp solid si conduc la abaterea paturii superficiale de la forma plana. Aceste fenomene sunt mai evidente în cazul tuburilor de sectiuni mici, numite capilare.
|
Fig.3.6 |
Sa presupunem un tub de raza r, asezat într-un lichid care uda peretii tubului si a carui tensiune superficiala este σ (Fig.3.6). Coloana de lichid va fi în echilibru atunci când presiunea suplimentara va fi egala cu cea hidrostatica.
In acest caz putem scrie:
![]() 3 (3.10)
3 (3.10)
si deci:
![]() 4(3.11)
4(3.11)
unde raza de curbura a suprafetei libere R s-a exprimat în functie de raza tubului r, prin relatia:
![]() 5 (3.12)
5 (3.12)
In raport cu valoarea unghiului θ are loc urcarea sau coborârea lichidului în tub. Formula (3.12) poarta numele de formula lui Jurin.
Fenomenul de capilaritate joaca un rol important în natura si în tehnica. Patrunderea apei în sol si în diferitele materiale poroase se produce datorita capilaritatii. Capilaritatea joaca un rol important si în hranirea plantelor. Pe fenomenul de capilaritate se bazeaza utilizarea fitilurilor, absorbirea apei de catre vata hidrofila, etc.
Majoritatea metodelor de determinare a tensiunii superficiale se bazeaza într-o masura mai mare sau mai mica pe modul în care este definita aceasta marime. O metoda folosita frecvent în practica este metoda stalagmometrica sau a picaturilor care foloseste o consecinta a fenomenelor superficiale, si anume formarea picaturilor care se scurg printr-un orificiu de diametru mic, de exemplu dintr-o pipeta. Dupa cum se poate vedea din figura 3.7, înainte de desprinderea picaturii zona de separatie dintre pipeta si picatura se îngusteaza, astfel încât picatura sa fie cât mai aproape de forma sferica. Desprinderea picaturii are loc în momentul în care greutatea acesteia egaleaza forta de tensiune superficiala în zona gâtuiturii, care trebuie sa fie egala cu σx2πa

De fapt, desprinderea picaturii este un fenomen brusc si studiul sau exact este complicat. Practic, se constata ca greutatea picaturii este proportionala cu raza exterioara a dispozitivului de picurare:
![]() (3.13)
(3.13)
Valoarea uzuala a constantei k este 0.7. Practic, se masoara masa unui numar dat de picaturi, de obicei 100, mai întâi pentru un lichid cu coeficientul de tensiune superficiala cunoscut, apoi pentru lichidul studiat. Facând raportul expresiei (3.13) pentru cele doua cazuri, se obtine:
![]() (3.14)
(3.14)
Metoda este foarte simpla si poate fi utilizata pentru a determina variatia coeficientului de tensiune superficiala în prezenta unor gaze diferite. De asemenea, facând o etalonare prealabila, poate fi determinata pe aceasta cale concentratia unei solutii.
Exista diverse metode de studiu a curgerii fluidelor si anume: metoda dezvoltata de J.Lagrange (1736-1813) constituie o dezvoltare a conceptelor mecanicii punctului material presupunând fiecare element de fluid ca un punct material. Mai convenabila este metoda dezvoltata de L.Euler (1707-1783) în care se studiaza viteza, presiunea si densitate în anumite puncte ale fluidului, la diferite momente. Vom utiliza în descrierea curgerii aceasta metoda. Vom defini câtiva parametri caracteristici curgerii fluidelor. Se numeste linie de curgere traiectoria urmata de un element de fluid în miscare, iar linia de curent (Fig.3.14) este curba la care vectorul viteza ramâne tangent în timpul curgerii.
|
1 Fig.3.14. |
|
2 Fig.3.15. |
Traiectoria unui element de fluid se refera la drumul parcurs în timp de acel element de fluid, iar linia de curent este o reprezentare instantanee a directiilor vitezelor unui ansamblu de elemente de fluid.
Suprafata determinata de mai multe linii de curent si care trece printr-o curba închisa C poarta numele de tub de curent (Fig.3.15).
Volumul de fluid care strabate, în unitatea de timp, o anumita sectiune transversala constituie debitul volumic:
![]() 6 (3.18)
6 (3.18)
Debitul masic este cantitatea de fluid care trece prin sectiunea transversala a unui tub de curent, în unitatea de timp:
![]() 7 (3.19)
7 (3.19)
Curgerea caracterizata prin constanta în timp dar nu si în spatiu a vectorului viteza, a presiunii si densitatii se numeste curgere stationara. In caz contrar, curgerea este nestationara.
O alta caracterizare a curgerii este ca ea poate fi rotationala sau irotationala. Daca elementul de fluid în fiecare punct nu are viteza unghiulara în jurul acelui punct, curgerea este irotationala. In caz contrar, ea este rotationala.
Dintr-un alt punct de vedere, curgerea poate fi compresibila sau incompresibila. Lichidele, si în anumite situatii gazele, pot fi considerate incompresibile.
|
3 Fig.3.16. |
Pentru a caracteriza din punct de vedere cinematic curgerea unui lichid se foloseste ecuatia de continuitate. Ecuatia de continuitate este o ecuatie diferentiala care exprima de fapt principiul conservarii masei unui fluid. Conform acestui principiu, cantitatea de fluid care intra minus cea care iese în unitatea de timp dintr-un volum elementar de fluid este egala cu variatia masei fluidului din elementul de volum respectiv. Formula matematica a continuitatii se obtine considerând într-un sistem de axe cartezian, un element de volum dV = dx dy dz, pentru care scriem diferentele dintre masa de fluid care intra si cea care iese în unitatea de timp, din acest element de volum (Fig.3.16).
Pe directia Ox intra în unitatea de timp masa:
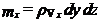 8 (3.20)
8 (3.20)
si iese:
![]() 9(3.21)
9(3.21)
Variatia de masa pe directia Ox va fi:
![]() 10 (3.22)
10 (3.22)
sau folosind (3.20):
![]() 11 (3.23)
11 (3.23)
Un calcul analog se face si pentru axele Oy si Oz. Principiul conservarii masei cere ca suma variatiilor obtinute, corespunzatoare celor trei directii, sa fie egala cu variatia masei din volumul elementar, în unitatea de timp:
![]() 12 (3.24)
12 (3.24)
Daca masa m = ρ dx dy dz, atunci din (3.23) si (3.24) rezulta:
![]() 13(3.25)
13(3.25)
care reprezinta ecuatia de continuitate si care în forma vectoriala are expresia:
![]() 14 (3.26)
14 (3.26)
Aceasta este forma cea mai generala a ecuatiei de continuitate putând fi aplicata si la fluide compresibile în curgere nestationara.
|
4 Fig.3.17. |
La fluide incompresibile, ρ = const. si ecuatia devine:
![]() 15 (3.27)
15 (3.27)
O alta forma a ecuatiei de continuitate se poate obtine în cazul unei conducte prin care trece un fluid, stiind ca prin fiecare sectiune a conductei trece, în unitatea de timp, aceeasi cantitate de fluid (Fig.3.17).
Daca prin sectiunea S1 trece în unitatea de timp volumul S1v1, cuprins între S1 si S1', atunci prin sectiunea S2 va trece volumul S2v2 cuprins între S2 si S2'. Punând conditia ca debitul masic este acelasi în cele doua sectiuni, putem scrie:
![]() 16(3.28)
16(3.28)
care reprezinta o alta forma a ecuatiei de continuitate. In cazul lichidelor care pot fi considerate incompresibile, ρ1 = ρ2, ecuatia se scrie sub forma:
![]() (3.29)
(3.29)
Dinamica fluidelor perfecte studiaza legile de miscare si comportarea fluidelor perfecte, supuse efectului unor forte care au drept consecinta deplasarea fluidului în raport cu un sistem de referinta.
|
5Fig.3.18. |
Sa stabilim ecuatia de miscare a fluidelor perfecte numita si ecuatia lui Euler. Pentru aceasta consideram un volum elementar de fluid si îi aplicam al doilea principiu al dinamicii, tinând seama de fortele masice care actioneaza asupra lui si de diferenta de presiune între cele doua fete ale paralelipipedului elementar, pe directia curgerii (Fig. 3.18).
Daca notam
cu![]() forta care actioneaza asupra
unitatii de masa de fluid, atunci forta masica are urmatoarele componente:
forta care actioneaza asupra
unitatii de masa de fluid, atunci forta masica are urmatoarele componente:
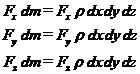 18(3.30)
18(3.30)
Aplicând principiul al doilea al dinamicii pentru elementul de fluid, pe directia Ox, avem:
![]() 19(3.31)
19(3.31)
Dupa simplificare si împartire cu ρ se obtine pentru directia Ox urmatoarea ecuatie:
![]() 20(3.32)
20(3.32)
Aceasta
relatie reprezinta ecuatia analitica de miscare
ale unui fluid perfect, stabilita de Euler. Daca scriem
ecuatiile corespunzatoare celor trei axe si le înmultim cu
versorii axelor ![]() si le
adunam, obtinem ecuatia vectoriala a lui Euler de
forma:
si le
adunam, obtinem ecuatia vectoriala a lui Euler de
forma:
![]() 22 (3.33)
22 (3.33)
Ecuatia lui Euler expliciteaza cele doua categorii de forte care actioneaza asupra fluidului, adica fortele masice si fortele de presiune.
|
6Fig.3.19. |
Principiul conservarii energiei se prezinta sub forma unei ecuatii, numita ecuatia lui Bernoulli. Ecuatia este valabila pentru un fluid perfect incompresibil în curgere stationara si irotationala.
Fie un tub de curent de forma celui din figura 3.19 asupra caruia singura forta de volum care actioneaza asupra sa este aceea datorata câmpului gravitational. Ecuatia lui Bernoulli se scrie sub forma:
![]() 23 (3.34)
23 (3.34)
In aceasta
ecuatie, expresia ![]() reprezinta presiunea dinamica sau energia
cinetica a unitatii de volum; p este presiunea statica sau energia unitatii
de volum corespunzatoare presiunii staticii, iar ρgz este presiunea
hidrostatica (de pozitie) sau energia potentiala a
unitatii de volum. Suma acestor presiuni reprezinta presiunea
totala, care este constanta într-o curgere stationara.
Aceasta afirmatie reprezinta legea lui Bernoulli.
reprezinta presiunea dinamica sau energia
cinetica a unitatii de volum; p este presiunea statica sau energia unitatii
de volum corespunzatoare presiunii staticii, iar ρgz este presiunea
hidrostatica (de pozitie) sau energia potentiala a
unitatii de volum. Suma acestor presiuni reprezinta presiunea
totala, care este constanta într-o curgere stationara.
Aceasta afirmatie reprezinta legea lui Bernoulli.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 370
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved