| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
FUNDAMENTELE STATICII MATRICEALE CLASICE
1 Deformarea statica a structurilor cu comportare liniar elastica
Cazul structurii cu o deplasare caracteristica
Fie structura (reductibila la un element structural) deformabila elastic, de rigiditate K, a carei axa longitudinala coincide cu directia axei de referinta X, blocata la un capat (numit nod si notat cu 1) si libera la capatul opus (numit nod si notat cu 2) unde, pe aceeasi directie, se produce deplasarea D si actioneaza static forta F (figura 1).
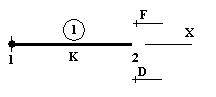
Figura 1 Element structural cu o deplasare caracteristica
Starea de deformare statica a structurii este complet caracterizata de relatia 1.1,
![]() (1.1)
(1.1)
care poate sa capete si o exprimare matriceala, de forma celei date de relatia 1.2,
![]() (1.2)
(1.2)
unde ![]() este matricea de rigiditate a structurii
este matricea de rigiditate a structurii
![]() - vectorul
deplasarii din capatul liber al structurii
- vectorul
deplasarii din capatul liber al structurii
![]() - vectorul fortei
din capatul liber al structurii.
- vectorul fortei
din capatul liber al structurii.
Cazul structurii cu doua deplasari caracteristice
Fie structura (reductibila la un element structural) deformabila elastic, de rigiditate K, a carei axa longitudinala coincide cu directia axei de referinta X, libera a se deplasa la ambele capete (numite noduri si notate cu 1, 2) unde, pe aceeasi directie, se produc deplasarile D1, D2 si actioneaza static fortele F1, F2 (figura 2).
Daca se face ipoteza ca structura se deformeaza elastic, dar în domeniul micilor deformatii, se poate aplica principiul suprapunerii efectelor si problema analizei de deformabilitate a structurii se reduce la rezolvarea a doua probleme de deformabilitate deja cunoscute:
- problema 1, corespunzând situatiei în care este liber a se deplasa capatul 1, D1≠0, si blocat capatul 2, D2=0, (figura 2a);
- problema 2, corespunzând situatiei în care este blocat capatul 1, D1=0, si liber a se deplasa capatul 2, D2≠0,(figura 2b).
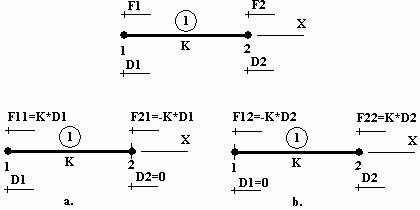
Figura 2 Element structural cu doua deplasari caracteristice
În cazul problemei 1, starea de deformare statica a structurii este complet caracterizata de relatia matriceala 1,
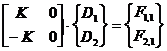 (1)
(1)
iar în cazul problemei 2, de relatia matriceala 2,
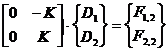 (2)
(2)
Indicii fortelor precizeaza, primul locul fortei (efectului), iar al doilea locul depasarii care a produs-o (cauzei).
În final, starea de deformare statica a structurii initiale este complet caracterizata de efectul sumat al celor doua situatii, respectiv ecuatia obtinuta prin sumarea matriceala a relatiilor 1 si 2, rezultând relatia matriceala 3.
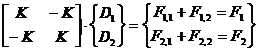 (3)
(3)
Relatia 3 poate capata si o forma compacta precum cea data de relatia 1.
Cazul structurilor cu mai multe deplasari caracteristice
Fie structura având doua elemente structurale deformabile elastic, de rigiditati K1 si K2, a caror axe longitudinale coincid cu directiile axelor proprii x si care ambele coincid cu directia axei de referinta a structurii X, având extremitatile primului element identice cu nodurile 1 si 2 ale structurii, respectiv ale celui de al doilea element identice cu nodurile 2 si 3 ale structurii, cuplate în nodul 2, noduri unde, pe aceeasi directie, se produc deplasarile D1, D2 si D3 si actioneaza static fortele F1, F2 si F3 (figura 3).
Daca se face ipoteza ca structura se deformeaza elastic, dar în domeniul micilor deformatii, se poate aplica principiul suprapunerii efectelor si problema analizei de deformabilitate a structurii se reduce la trei probleme de deformabilitate deja cunoscute:
- problema 1, corespunzând situatiei în care este liber a se deplasa nodul 1, D1≠0, si blocate nodurile 2, 3, D2=D3=0, (figura 3a);
- problema 2, corespunzând situatiei în care este liber a se deplasa nodul 2, D2≠0, si blocate nodurile 1, 3, D1=D3=0, (figura 3b);
- problema 3, corespunzând situatiei în care este liber a se deplasa nodul 3, D3≠0, si blocate nodurile 1, 2, D1=D2=0, (figura 3c).
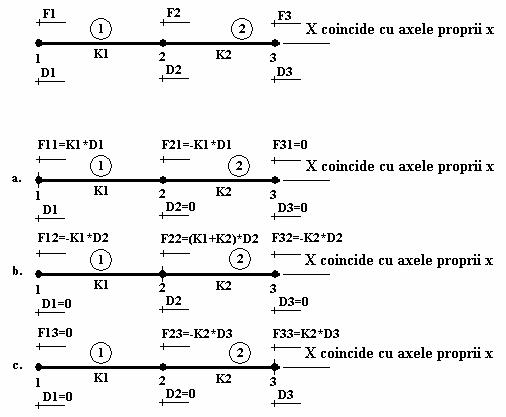
Figura 3 Structura cu doua elemente componnte
În cazul problemei 1, starea de deformare statica a structurii este complet caracterizata de relatia matriceala 3.1;
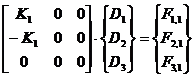 (3.1)
(3.1)
în cazul problemei 2, de relatia matriceala 3.2;
 (3.2)
(3.2)
în cazul problemei 3, de relatia matriceala 3.3.
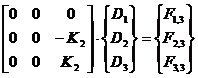 (3.3)
(3.3)
Indicii fortelor precizeaza, primul locul fortei (efectului), iar al doilea locul depasarii care a produs-o (cauzei).
În final, starea de deformare static a structurii initiale este complet caracterizata de efectul sumat al celor trei situatii, respectiv ecuatia obtinuta prin sumarea matriceala a relatiilor 3.1, 3.2 si 3.3, cu obtinerea relatiei 3.4.
 (3.4)
(3.4)
Relatia 3.4 poate sa capete si o forma compacta precum, cea data de relatia 1.
Din punctul de vedere matematic, relatia 3.4 poate fi privita ca suma relatiilor 4.1 si 4.
 (4.1)
(4.1)
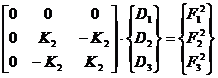 (4.2)
(4.2)
Prin eliminarea liniilor si coloanelor, din matricele de rigiditate, care au toate elementele egale cu zero, relatiile 4.1 si 4.2 devin cele din relatiile 5.1 si 5.
 (5.1)
(5.1)
si
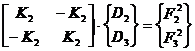 (5.2)
(5.2)
Aduse la aceasta forma, relatiile 5.1 si 5.2 caracterizeaza starea de deformare statica a elementului structural 1, respectiv 2 (a se vedea relatia 3), unde indicii superiori precizeaza apartenenta la element.
Relatiile matriceale 5.1 si 5.2 reprezinta echilibrul, static, raportat (numai) la parametrii structurali aferenta: principali D1, D2 si secundari F1, F2 pentru elementul structural 1, respective, principali D2, D3 si secundari F2, F3 pentru elementul structural
Relatiile 4.1 si 4.2 reprezinta echilibrul static, raportat la (toti) parametrii structurii: principali D1, D2, D3 si secundari F1, F2, F3, pentru cele doua elemente structurale.
2 Metoda staticii matriceale clasice exprimarea în deplasari
1 Prezentarea generala a metodei
Cazul 3, tratat în paragraful 1, poate fi generalizat pentru o structura cu un numar oarecare de elemente, a caror axe longitudinale coincid cu directiile axelor proprii x si care toate coincid cu directia axei de referinta a structurii X. Generalizarea poate fi facuta si pentru situatia în care coincidenta nu are loc, definind parametri si sisteme de referinta proprii elementului, precum si un mod de proiectie a parametrilor în sistemul de referinta al structurii.
Cazul 3, conduce si la stabilirea unui proces de calcul sistematizat, etapizat, bazat pe ideea ca starea de deformare a unei structuri poate fi cunoscuta daca se cunoaste ecuatia matriceala ce caracterizeaza starea de deformare a fiecarui element structural (ecuatia de echilibru). Aceasta concluzie pune bazele calculului matriceal, în forma sa clasica, prezentata în continuare, particularizata pentru cazul exprimarii în deplasari a metodei (parametrii principali fiind deplasarile actionând la extremitati sau noduri si cei secundari fortele crespunzatoare deplasarilor).
Etapa 1. Stabilirea ecuatiei matriceale de echilibru pentru fiecare element structural:
- etapa 1.1: prin raportare la parametrii proprii;
- etapa 1.2: prin raportare la parametrii structurali aferenti;
- etapa 1.3: prin raportare la parametrii structurii.
Etapa Stabilirea ecuatiei matriceale de echilibru a structurii, prin sumarea ecuatiilor matriceale de echilibru a tuturor elementelor sau asamblarea acestora (raportarea facându-se la parametrii structurii).
Etapa 3. Introducerea conditiilor la limita de tip
- Dirichlet, prin restrictionarea parametrilor principali (impunerea deplasarilor la nodurile structurii);
- Neumann, prin restrictionarea parametrilor secundari (impunerea fortelor ce actioneaza la nodurile structurii);
- Cauchy, prin restrictionarea conlucrarii cu mediul adiacent (impunerea conlucrarii cu mediul adiacent prin definirea caracteristicii elestice a acestuia).
Etapa 4. Determinarea parametrilor principali (deplasarilor necunoscute din nodurile structurii) prin rezolvarea sistemului de ecuatii rezultat în urma ridicarii nedeterminarii matematice si statice cu ocazia impunerii conditiilor la limita.
Odata ce parametrii principali (deplasarile nodurilor structurii) sunt cunoscute, metoda staticii matriceale clasice (exprimarea în deplasari) ia sfârsit, urmând ca alte rezultate sa fie stabilite în etape auxuiliare: determinarea parametrilor secundari necunoscuti (fortelor din rezemari) sau eforturilor din elementele structurii.
2 Introducerea conditiilor la limita de tip Dirichlet si Neumann
În metoda staticii matriceale clasice, introducerea conditiilor la limita de tip Dirichlet si Neumann (Etapa 3) se poate face în baza unui proces de calcul etapizat, asa cum se va prezenta în continuare, cu particularizarea necesara pentru cazul exprimarii în deplasari a metodei.
Etapa 3.1. Identificarea valorilor parametrilor secundari restrictionati (fortelor nodale impuse) si înlocuirea în vectorul corespunzator (al fortelor, F).
Etapa 3. Identificarea coloanei din matricea de rigiditate, K, corespunzând parametrului principal restrictionat (deplasarii impuse), indexul coloanei fiind identic cu indexul parametrului, si sumarea elementelor acesteia, cu semn schimbat, la elementele corespondente din vectorul fortelor, dupa ce au fost multiplicate cu valoarea parametrului principal (deplasarii); operatiunea se repeata pentru fiecare parametru restrictionat (deplasare impusa).
Etapa 3.3. Identificarea ecuatiilor din sistem si a coloanelor din matricea de rigiditate corespunzând parametrilor principali restrictionati (deplasari impuse) si eliminarea acestora.
Sistemul ecuatiilor de echilibru, redus la numarul deplasarilor necunoscute, poate fi rezolvat pentru ca determinantul asociat matricei de rigiditate (redusa si ea) este diferit de zero, iar solutia sistemului este unica.
3 Aplicatie la analiza statica a structurilor
Enuntarea problemei: Fie structura formata din trei elemente structurale coaxiale, având rigiditatile K1=1000KN/m, K2=2000KN/m, K3=1000KN/m, cu deplasarile blocate la nodurile extreme si actionata în nodurile de cuplaj de doua forte egale cu 10KN si 20KN (figura 4).

Figura 4 Modelul cu elemente structurale al ansamblului mecanic
Rezolvarea problemei
Etapa 1. Stabilirea ecuatiei maticeale de echilbru static pentru fiecare element structural:
- etapa 1.1: prin raportare la parametrii proprii - nu este cazul;
- etapa 1.2: prin raportare la parametrii structurali aferenti:
elementrul structural 1

elementul structural 2
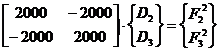
elementul structural 3
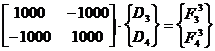
- etapa 1.3: prin raportare la parametrii structurali:
elementul structural 1

elementul structural 2
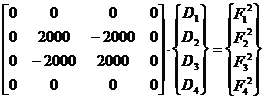
elementul structural 3
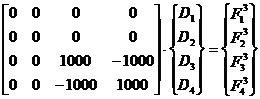
Etapa Stabilirea ecuatiei matriceale de echilibru static a structurii:

Etapa 3. Introducerea conditiilor la limita de tip Neumann si Dirichlet:
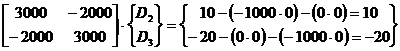
Etapa 4. Determinarea deplasarilor necunoscute:
- se rezolva sistemul de ecuatii din etapa precedenta, rezultând:
D2= -0.002 m
D3= -0.008 m
Etapa 5 (auxiliara). Determinarea fortelor din reazeme:
- se utilizeaza ecuatiile 1 si 4 din sistemul de la Etapa 2, eliminate prin introducerea conditiilor la limita, corespunzatoare deplasarilor restrictionate si pe directia carora apar fortele din reazeme F1 si F4:
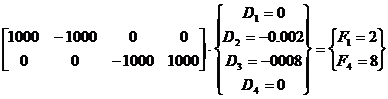
- suma fortelor din reazeme (2KN+8KN=10KN) este egala cu suma actiunilor (10KN-20KN= -10KN), evident cu semn minus; aceast fapt constituie o verificare a corectitudinii rezultatelor.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 279
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved