| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Studiul raspunsului la semnal treapta al elementelor de tip PT1. Utilizarea acestuia la identificarea elementelor de tip PT1.
1.Modelul matematic intrare‑iesire
Modelul matematic intrare-iesire in domeniul timpului al acestor elemente este:
![]() (1)
(1)
sau, impartind reltia (1) cu a![]()
![]() (2)
(2)
in care:
T ‑ constanta de timp a elementului
K ‑ coeficientul de transfer al elementului.
![]() (3)
(3)
1.2. Modelul matematic in domeniul complex corespunzator modelului (1), respectiv (2), va fi:
![]() (4) sau:
(4) sau:
![]()
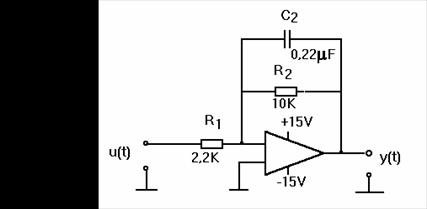

2. Realizarea unui circuit electronic de tip PT1
-model electronic al acestora ‑ este posibil cu ajutorul unui amplificator operational, asa cum se arata in figura 1.
Functia de transfer, conform celor aratate va fi:
![]() (5)
(5)
adica expresia (2), in care:
![]() (6)
(6)
![]() (7)
(7)
4. Modelul matematic in domeniul timpului al circuitului electronic considerat, corespunzator rela]iei (5), va fi:
![]() (8)
(8)
5. Raspunsul teoretic la un semnal treapta:
![]() (9)
(9)
va fi solutia ecuatiei diferentiale (2) sau (7), adica:
![]() (10)
(10)
sau
![]() (11)
(11)
avand aspectul aratat in figura 2.
6. Determinarea experimentala a raspunsului la semnal treapta.
6.1. Se va realiza circuitul din figura 3, utilizand un amplificator operational indicat de catre conducatorul lucrarii. In vederea repetarii semnalului de intrare, pentru a putea vizualiza raspunsul elementului de studiat pe ecranul osciloscopului, va fi utilizat un generator de impulsuri dreptunghiulare.
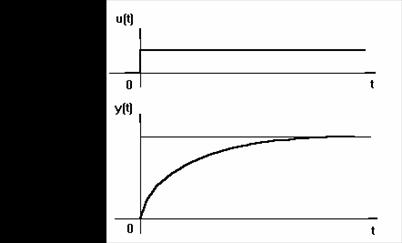
Fig.2 Raspunsul teoretic la semnal treapta u(t)=u
al elementelor de tip PT 1
6.2. Se vor aplica semnale treapta repetate cu frecven]a indicata de catre conducatorul lucrarii.
6.3. Se va vizualiza semnalul de intrare la osciloscop si se va determina valoarea lui.
6.4. Se va vizulaliza semnalul de iesire pe ecranul osciloscopului, masurindu‑se valorile semnalului la diferite valori ale timpului, trecand rezultatele intr‑un tabel de forma tabelului 1.
Tabelul 1.
|
t |
mm |
|
s |
|
|
y |
mm |
|
s |
6.5. Utilizand datele experimentale din tabelul 1, se va construi graficul raspunsului curcuitului considerat.
6.6. Utilizand relatia (10), se va calcula si pe cale analitica raspunsul la treapa si se va reprezenta alaturi de cel experimental, interpretandu‑se rezultatele obtinute.
7. Determinarea modelului matematic intrare‑iesire cu ajutorul raspunsului la treapta experimental.
Valorile constantelor K si T, care intervin in expresia modelului matematic pot fi determinate tinand seama de urmatoarele:
intre semnalul treapta de la intrare, raspunsul la treapta si coeficientul k exista relatia:
![]() (12)
(12)
2) constanta T este egala cu valoarea timpului pentru care y(t) atinge valoarea 0,632*y(¥) (vezi figura 4)
![]() (13)
(13)
|
|
Se va verifica valabilitatea modelului matematic determinat mai sus, calculand raspunsul
![]() (14)
(14)
in care, pentru K si T vor fi utilizate valorile determinate in modul aratat, si comparandu‑l cu raspunsul determinat pe cale experimentala.
Fig.4 Montaj pentru determinarea raspunsului la trapta al elementelorde tip PT1

|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1654
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved