| CATEGORII DOCUMENTE |
DOCUMENTE SIMILARE |
|||
|
|||
Teoria estimatiei
Relativ la colectivitatea ![]() este cercetatǎ
caracteristica
este cercetatǎ
caracteristica ![]() , care urmeazǎ legea de probabilitate datǎ prin
functia de probabilitate
, care urmeazǎ legea de probabilitate datǎ prin
functia de probabilitate ![]() ce reprezintǎ
functia frecventa dacǎ
ce reprezintǎ
functia frecventa dacǎ ![]() este de tip discret,
respectiv densitatea de probabilitate in cazul continuu, iar
este de tip discret,
respectiv densitatea de probabilitate in cazul continuu, iar ![]() este un parametru
necunoscut.
este un parametru
necunoscut.
Teoria estimatiei are ca scop
evaluarea parametrulor de care depinde legea de probabilitate a caracteristicii
![]() , folosind datele de selectie
, folosind datele de selectie ![]() ,
, ![]() ,,
,,![]() si bazandu-se pe rezultatele teoretice relative la
variabilele de selectie
si bazandu-se pe rezultatele teoretice relative la
variabilele de selectie ![]() ,
, ![]() ,,
,,![]()
Definitia 1. Numim
functie de estimatie (punctualǎ) sau estimator al parametrului ![]() functia de
selectie (statistica)
functia de
selectie (statistica)
![]()
cu ajutorul cǎreia se obtin
concluzii relative la parametrul ![]()
Definitia Spunem cǎ functia de estimatie ![]() este functie de
estimare consistentǎ sau estimatoar consistent pentru parametrul
necunoscut
este functie de
estimare consistentǎ sau estimatoar consistent pentru parametrul
necunoscut ![]() , dacǎ
, dacǎ ![]()
pentru orice numǎr ![]() adicǎ
adicǎ ![]() iar valoarea numericǎ
iar valoarea numericǎ
![]() se numeste
estimatie consistentǎ pentru parametrul
se numeste
estimatie consistentǎ pentru parametrul ![]()
Definitia 3. Numim
functie de estimatie (estimator) absolut corectǎ pentru
parametrul ![]() functia de
estimatie
functia de
estimatie
![]()
care satisface conditiile
(i) ![]()
(ii) 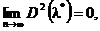
iar valoare numericǎ
![]() se numeste
estimatie absolut corectǎ pentru parametrul
se numeste
estimatie absolut corectǎ pentru parametrul ![]()
Definitia 4. Numim functie
de estimatie (estimator) corectǎ pentru parametrul ![]()
functia de estimatie ![]() care satisface
conditiile
care satisface
conditiile
(i) ![]()
(ii) 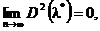
iar valoarea numericǎ
![]() se numeste
estimatie corectǎ pentru parametrul
se numeste
estimatie corectǎ pentru parametrul ![]()
Definitia 5. Numim
distorsiunea (deplasarea) estimatorului ![]() al parametrului
al parametrului ![]() , diferenta
, diferenta ![]() iar daca
distorsiunea este nula estimatorul
iar daca
distorsiunea este nula estimatorul ![]() se numeste
nedeplasat.
se numeste
nedeplasat.
Proprietatea 6.
Daca ![]() este un estimator
absolut corect pentru parametrul
este un estimator
absolut corect pentru parametrul ![]() , atunci estimatorul este consistent.
, atunci estimatorul este consistent.
Demonstratie. Avand in
vedere ca ![]() inegalitatea lui
Cebisev pentru variabila aleatoare
inegalitatea lui
Cebisev pentru variabila aleatoare ![]() este
este
![]() pentru
pentru ![]()
Dar 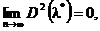 si trecand la
limita in inegalitatea lui Cebasev se obtine
si trecand la
limita in inegalitatea lui Cebasev se obtine ![]() pentru orice
pentru orice ![]() deci
deci ![]() este un estimator
consistent pentru parametrul
este un estimator
consistent pentru parametrul ![]()
Exemplul 7. Fie
caracteristica ![]() pentru care
exista momentul teoretic de ordinul
pentru care
exista momentul teoretic de ordinul ![]() ,
, 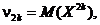 si fie o
selectie repetata de volum
si fie o
selectie repetata de volum ![]() , atunci momentul de selectie de ordin
, atunci momentul de selectie de ordin ![]() este
este ![]() Vom arata ca
Vom arata ca
![]() este estimator absolut
corect pentru momentul teoretic de ordin
este estimator absolut
corect pentru momentul teoretic de ordin ![]() , adica pentru
, adica pentru ![]()
Pentru aceasta scriem succesiv
![]()
respectiv
![]()
cand ![]() de unde se obtine
ca
de unde se obtine
ca ![]() este estimator absolut
corect pentru parametrul
este estimator absolut
corect pentru parametrul ![]()
Observatia 8. Media de
selectie ![]() este estimator absolut
corect pentru media teoretica
este estimator absolut
corect pentru media teoretica ![]()
Exemplul 9. Momentul centrat de selectie de ordinul doi
![]()
este functie de
estimatie corecta pentru momentul centrat teoretic de orinul doi ![]() adica pentru
dispersia teoretica.
adica pentru
dispersia teoretica.
Sa se arate ca
![]() cand
cand ![]()
respectiv
![]() pentru
pentru ![]()
Daca se considera functia de estimatie care defineste dispersia de selectie
![]()
aceasta este
functie de estimatie absolut corecta pentru dispersia teoretica
![]()
Pentru aceasta avem
ca ![]() Prin urmare, se
obtine
Prin urmare, se
obtine
![]()
respectiv
![]() cand
cand ![]()
In
consecinta ![]() este functie de estimatie absolut
corecta pentru dispersia teoretica
este functie de estimatie absolut
corecta pentru dispersia teoretica ![]()
Definitia 10. Numim cantitatea de
informatie (a lui Fisher) a unei selectii de volum ![]() relativ la parametrul
relativ la parametrul![]() necunoscut,
valoarea
necunoscut,
valoarea
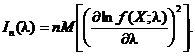
Observatia 11 (Inegalitatea
Rao-Cramer). Estimatorul absolut corect ![]() al parametrului
al parametrului ![]() satisface inegalitatea
satisface inegalitatea
![]()
Definitia 1
Estimatorul ![]() , absolut corect pentru parametrul necunoscut
, absolut corect pentru parametrul necunoscut ![]() , se numeste eficient, daca
, se numeste eficient, daca ![]() iar raportul
iar raportul
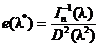
se numeste eficienta estimatorului ![]()
Exemplul 13. Sa
verificam daca media de selectie, in cazul cand caracteristica
cercetata are distributia ![]() este functie de
estimatie eficienta pentru parametrul
este functie de
estimatie eficienta pentru parametrul ![]()
Se stie ca media de
selectie ![]() este functie de
estimatie absolut corecta pentru media teoretica
este functie de
estimatie absolut corecta pentru media teoretica ![]()
Functia de frecventa a caracteristicii ![]() este data prin
este data prin
![]() pentru
pentru ![]() si
si ![]()
Se vede ca ![]() si
si ![]() adica
probabilitatile din distributia caracteristicii
adica
probabilitatile din distributia caracteristicii ![]()
Pentru a calcula cantitatea de
informatie relativa la parametrul ![]() avem ca
avem ca

deci ![]()
Pe de alta parte, se poate scrie
![]()
Prin urmare se
obtine ca ![]() deci
deci ![]() este estimator
eficient pentru parametrul
este estimator
eficient pentru parametrul ![]()
1. Metoda verosimilitatii maxime
Fie ![]() caracteristica
cercetata, care are functia
caracteristica
cercetata, care are functia ![]() de probabilitate, ce o
caracterizeaza si care depinde de parametrii necunoscuti
de probabilitate, ce o
caracterizeaza si care depinde de parametrii necunoscuti ![]() ,
, ![]() , ,
, , ![]()
Deoarece variabilele de
selectie ![]() ,
, ![]() , ,
, ,![]() sunt variabile aleatoare independente si urmeaza
aceeasi lege de probabilitate ca
sunt variabile aleatoare independente si urmeaza
aceeasi lege de probabilitate ca ![]() , rezulta ca vectorul aleator (
, rezulta ca vectorul aleator (![]() ,
, ![]() , ,
, ,![]() ) va avea functia de probabilitate
) va avea functia de probabilitate
![]()
si care poarta numele de functie de verosimilitate.
Definitia 14. Spunem
ca estimatorii ![]() sunt estimatori de
verosimilitate maxima, respectiv pentru parametrii
sunt estimatori de
verosimilitate maxima, respectiv pentru parametrii ![]()
![]() daca realizeaza
maximul functiei de verosimilitate.
daca realizeaza
maximul functiei de verosimilitate.
Observatia 15. Determinarea estimatorilor de verosimilitate maxima se obtine prin rezolvarea sistemului de ecuatii
![]()
Acest sistem, de regula se inlocuieste cu sistemul
![]()
care conduce la aceeasi solutie si care se numeste sistemul de verosimilitate maxima.
Observatia 16. Un estimator eficient este un estimator de verosimilitate maxima.
Observatia 17. Un
estimator de verosimilitate maxima este estimator consistent, iar pentru
valori mari ale volumului ![]() este o variabila
aleatoare ce urmeaza legea normala
este o variabila
aleatoare ce urmeaza legea normala ![]() unde
unde ![]() este parametrul
estimat.
este parametrul
estimat.
Exemplul 18. Sa
determinam estimatorii de verosimilitate maxima pentru valoarea medie
si abaterea standard, daca se considera caracteristica ![]() care urmeaza
legea normala
care urmeaza
legea normala ![]()
Se stie ca ![]() si
si ![]() iar
iar 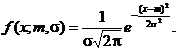
Pentru a scrie sistemul de verosimilitate maxima, avem ca
![]()
de unde
![]()
In acest mod se obtine
![]()
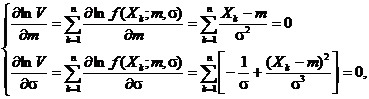
sau
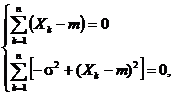
de unde se obtin estimatorii de verosimilitate maxima
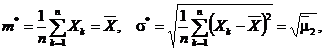
pentru parametrii ![]() si
si ![]()
Metoda momentelor
Fie caracteristica ![]() de probabilitate
si care depinde de
de probabilitate
si care depinde de ![]() parametrii
parametrii ![]() ,
, ![]() , ,
, , ![]()
Metoda momentelor consta in
estimarea acestor parametrii din conditiile ca momentele teoretice
initiale ale caracteristicii ![]() au ca estimatori
absolut corecti pe momentele de selectie de ordin corespondent.
Astfel, se obtine sistemul de ecuatii
au ca estimatori
absolut corecti pe momentele de selectie de ordin corespondent.
Astfel, se obtine sistemul de ecuatii ![]() pentru
pentru ![]() din care se obtin
estimatii pentru parametrii
din care se obtin
estimatii pentru parametrii ![]() ,
, ![]() , ,
, , ![]()
Exemplul
19. Se considera caracteristica ![]() , care urmeaza legea gamma de parametrii
, care urmeaza legea gamma de parametrii ![]() necunoscuti. Vom
estima acesti parametri, folosind metoda momentelor, pe baza datelor
necunoscuti. Vom
estima acesti parametri, folosind metoda momentelor, pe baza datelor ![]() ,
, ![]() ,,
,, ![]() de selectie.
de selectie.
Functia densitate
de probabilitate a caracteristicii ![]() este
este
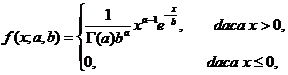
unde ![]() este functia
Euler de speta a doua, adica
este functia
Euler de speta a doua, adica 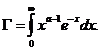
In cazul de fata este
vorba de doi parametri, deci sistemul de ecuatii este format din doua
ecuatii, anume ![]() si
si ![]()
Vom calcula momentul
teoretic initial ![]() de ordin
de ordin ![]() , adica
, adica
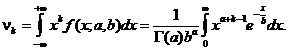
Daca se face schimbarea de variabila ![]() se obtine
se obtine
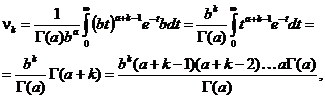
deci ![]() Rezulta astfel
sistemul
Rezulta astfel
sistemul
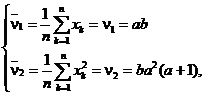
care are solutia
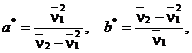
ceea ce reprezinta estimatorii pentru parametrii ![]() si respectiv
si respectiv ![]()
3. Metoda intervalelor de incredere
Fie caracteristica ![]() cercetata avand
functia de probabilitate
cercetata avand
functia de probabilitate ![]() unde
unde ![]() este unparametru
necunoscut.
este unparametru
necunoscut.
Metoda intervalelor de incredere
consta in determinarea a doua functiide selectie ![]() si
si ![]() astfel incat
astfel incat ![]() unde
unde ![]() nu depinde de
nu depinde de ![]() si se
numeste probabilitate de risc, iar
si se
numeste probabilitate de risc, iar ![]() se numeste
probabilitate de incredere.
se numeste
probabilitate de incredere.
Intervalul aleator ![]() se numeste
interval de incredere pentru parametrul
se numeste
interval de incredere pentru parametrul ![]()
De regula, pentru a construi un
interval de incredere pentru parametrul ![]() , se cauta determinarea caracteristicii
, se cauta determinarea caracteristicii ![]() a carei lege de
probabilitate sa fie cunoscuta, lege de probabilitate care sa nu
depinda de parametrul
a carei lege de
probabilitate sa fie cunoscuta, lege de probabilitate care sa nu
depinda de parametrul ![]() .
.
Se determina apoi
un interval numeric ![]() astfel incat
astfel incat
![]()
Din dubla inegalitate ![]() se exprima
parametrul
se exprima
parametrul ![]() prin dubla inegalitate
prin dubla inegalitate
![]() echivalenta cu cea de dinainte.
echivalenta cu cea de dinainte.
Desigur, in aplicatiile
practice, intervalul aleator este inlocuit cu intervalul numeric corespunzator
![]() , iar acesta este cu atat mai bun cu cat are lungime mai
mica si cu cat probabilitatea de incredere
, iar acesta este cu atat mai bun cu cat are lungime mai
mica si cu cat probabilitatea de incredere ![]() este mai mare.
este mai mare.
Exemplul 20.
(Intervalul de incredere pentru media teoretica daca dispersia este
cunoscuta). Se considera caracteristica ![]() ce urmeaza legea
normala
ce urmeaza legea
normala ![]() , unde
, unde ![]() este necunoscut, iar
este necunoscut, iar ![]() este cunoscut.
este cunoscut.
Pentru construirea unui interval de
incredere pentru media teoretica ![]() necunoscuta
efectuam o selectie repetata de volum
necunoscuta
efectuam o selectie repetata de volum ![]() si
consideram probabilitatea de incredere
si
consideram probabilitatea de incredere ![]() data,
data, ![]() .
.
Conform Observatiei 1.17 avem ca caracteristica
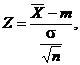 unde
unde ![]()
urmeaza legea
normala ![]() prin urmare o lege de
probabilitate cunoscuta ce nu depinde de parametrul necunoscut
prin urmare o lege de
probabilitate cunoscuta ce nu depinde de parametrul necunoscut ![]() Rezulta ca
putem determina intervalul numeric
Rezulta ca
putem determina intervalul numeric ![]() astfel incat
astfel incat
![]()
adica ![]() unde
unde 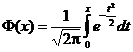 este functia lui
Laplace si care este tabelata in Anexa I.
este functia lui
Laplace si care este tabelata in Anexa I.
Desigur ca intervalul numeric ![]() nu este in mod unic determinat.
Intervalul de incredere de lungime minima pentru
nu este in mod unic determinat.
Intervalul de incredere de lungime minima pentru ![]() fixat se obtine
cand este simetric fata de origine, adica
fixat se obtine
cand este simetric fata de origine, adica ![]() In acest caz
In acest caz ![]() va fi dat prin
relatia
va fi dat prin
relatia
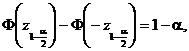 adica
adica 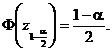
Cand se foloseste functia lui Laplace definita prin
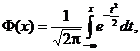
atunci ![]() se determina din relatia
se determina din relatia 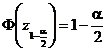 si
reprezinta de fapt cuantila de ordin
si
reprezinta de fapt cuantila de ordin ![]()
Odata determinat
intervalul ![]() , putem scrie
, putem scrie
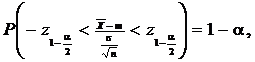
sau
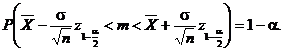
Prin urmare,
intervalul de incredere pentru media teoretica ![]() este
este ![]() unde
unde
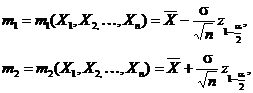
iar ![]()
Observatia 21. Cand
caracteristica ![]() nu urmeaza legea
normala, dar volumul selectiei este mare
nu urmeaza legea
normala, dar volumul selectiei este mare ![]() si se
cunoaste abaterea medie patratica teoretica
si se
cunoaste abaterea medie patratica teoretica ![]()
![]() atunci statistica
atunci statistica
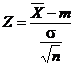 ,
,
unde ![]() este media teoretica (necunoscuta),
este aproximativ repartizata normal
este media teoretica (necunoscuta),
este aproximativ repartizata normal ![]()
Prin urmare, poate fi considerat
intervalul de incredere pentru parametrul ![]() , cu probabilitatea de incredere
, cu probabilitatea de incredere ![]() , intervalul obtinut la exemplul precedent.
, intervalul obtinut la exemplul precedent.
Exemplul 22 (Interval de incredere pentru media teoretica cand dispersia teoretica este necunoscuta).
Fie caracteristica ![]() ce urmeaza legea
normala
ce urmeaza legea
normala ![]() , unde parametrul
, unde parametrul ![]() este necunoscut, iar
este necunoscut, iar ![]() este de asemenea
parametru necunoscut. Pentru a construi un interval de Incredere pentru media
teoretica
este de asemenea
parametru necunoscut. Pentru a construi un interval de Incredere pentru media
teoretica ![]() , cu o probabilitate de incredere
, cu o probabilitate de incredere ![]() data, vom
considera statistica
data, vom
considera statistica
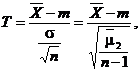
unde
![]() si
si ![]()
Pe baza
observatiei 1.22, avem ca statistica ![]() urmeaza legea
Student cu
urmeaza legea
Student cu ![]() grade de libertate.
Asadar, putem determina intervalul numeric
grade de libertate.
Asadar, putem determina intervalul numeric 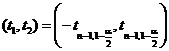 astfel incat
astfel incat ![]() adica
adica ![]() unde
unde
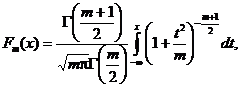
![]()
este functia de
repartitie a legii Student cu ![]() grade de libertate
si care este tabelata, pentru anumite valori, in Anexa II.
grade de libertate
si care este tabelata, pentru anumite valori, in Anexa II.
Prin urmare ![]()
![]() se determina ca
se determina ca 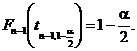
Odata determinat
intervalul ![]() , putem scrie
, putem scrie
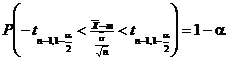
sau
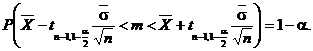
Astfel s-a
obtinut intervalul de incredere ![]() pentru media
teoretica
pentru media
teoretica ![]() , unde
, unde
![]()
![]()
Exemplul 23
(Intervalul de incredere pentru diferenta mediilor a doua
populatii). Fie doua populatii ![]() si
si ![]() pentru care se
cerceteaza aceeasi caracteristica. Fie aceasta
caracteristica
pentru care se
cerceteaza aceeasi caracteristica. Fie aceasta
caracteristica ![]() ce urmeaza legea
legea normala
ce urmeaza legea
legea normala ![]() pentru populatia
pentru populatia ![]() si respectiv
si respectiv ![]() ce urmeaza legea
normala
ce urmeaza legea
normala ![]() pentru populatia
pentru populatia ![]() .
.
Vom determina un
interval de incredere, cu probabilitatea de incredere ![]() , pentru diferenta
, pentru diferenta ![]()
Pentru aceasta se considera
doua selectii independente relative la cele doua populatii,
cu variabilele de selectie corespunzatoare ![]() ,
, ![]() ,,
,, ![]() si respectiv
si respectiv ![]() ,
, ![]() ,,
,, ![]()
Distingem, in continuare, doua cazuri.
a) Abaterile standard ![]() si
si ![]() cunoscute. In acest
caz, pe baza Observatiei 1.18, avem ca statistica
cunoscute. In acest
caz, pe baza Observatiei 1.18, avem ca statistica
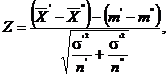
unde ![]() si
si ![]() urmeaza legea
normala
urmeaza legea
normala ![]() Ca la Exemplul 20, se
determina intervalul numeric notat prin
Ca la Exemplul 20, se
determina intervalul numeric notat prin 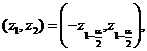 astfel incat
astfel incat ![]() adica
adica
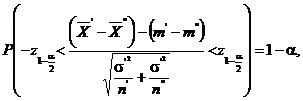
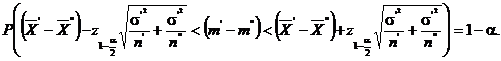
Aceasta
relatie ne da intervalul de incredere pentru diferenta ![]() a mediilor celor doua populatii.
a mediilor celor doua populatii.
b)
Abaterile standard ![]() necunoscute. In acest
caz, se considera statistica
necunoscute. In acest
caz, se considera statistica
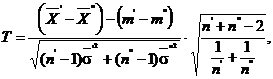
unde ![]() si
si ![]() sunt mediile de
selectie definite ca mai inainte,
sunt mediile de
selectie definite ca mai inainte, ![]() si
si ![]() sunt dispersiile de
selectie, adica
sunt dispersiile de
selectie, adica
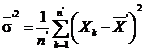 si
si 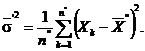
Statistica
T urmeaza legea Student cu ![]() grade de libertate.
grade de libertate.
In continuare, ca la exemplul 22,
pentru o probabilitate de incredere ![]() , se determina intervalul
, se determina intervalul 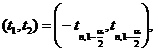 astfel ca
astfel ca ![]() , adica
, adica
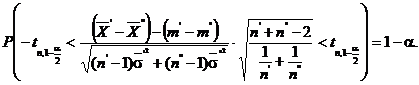
Astfel se obtine intervalul de incredere
pentru diferenta ![]()
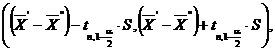
unde
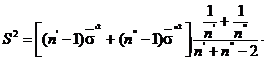
Exemplul 24
(Interval de incredere pentru dispersia teoretica). Se considera caracteristica X ce urmeaza legea normala ![]() . Pentru a construi un interval de incredere pentru dispersia
teoretica,
. Pentru a construi un interval de incredere pentru dispersia
teoretica, ![]() , se construieste statistica
, se construieste statistica
![]() , unde
, unde ![]() ,
, ![]() .
.
Conform Observatiei 1.22, statistica H2 urmeaza legea ![]() cu n-1 grade de libertate.
Astfel, pentru probabilitatea de incredere
cu n-1 grade de libertate.
Astfel, pentru probabilitatea de incredere ![]() , se poate determina intervalul numeric
, se poate determina intervalul numeric ![]() , astfel ca
, astfel ca ![]() .
.
Anume, ![]() se determina din
relatia
se determina din
relatia ![]() , respectiv
, respectiv ![]() se determina din
relatia
se determina din
relatia ![]() , unde
, unde ![]() este functia de
repartitie pentru legea
este functia de
repartitie pentru legea ![]() cu m grade de
libertate, adica
cu m grade de
libertate, adica
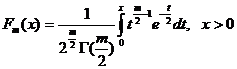 ,
,
care este tabelata in Anexa III.
Odata determinat intervalul ![]() , putem scrie ca
, putem scrie ca
![]() ,
,
sau
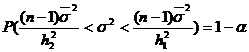 .
.
Prin urmare, s-a obtinut intervalul de incredere ![]() pentru parametrul
pentru parametrul ![]() , unde
, unde
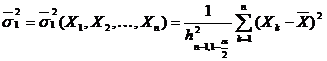 ,
,
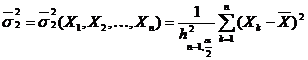 .
.
Observatia 25. Cu notatiile de la exemplul precedent,
intervalul de incredere pentru abaterea standard teoretica ![]() este
este ![]() .
.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3994
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved