Parametrii tendintei centrale

Parametrii tendintei centrale

Parametrii din aceasta grupa au menirea de a evidentia pozitia in jurul careia se grupeaza ansamblul valorilor unei variabile de la baza unei serii. Aceasta pozitie exprimata printr-un numar se numeste pozitie centrala. Ea poate fi evidentiata prin:

- valoarea medie ;

- valoarea mediana ;

- valoarea modala .

A. Valoarea medie

Valoarea medie reprezinta principalul parametru care caracterizeaza tendinta centrala a unei repartitii statistice.

In vederea definirii parametrului valoarea medie se considera o populatie statistica studiata in raport cu variabila cantitativa X si o functie G(x₁,x₂,.,x_R) unde x_i, , reprezinta starile variabilei X. Functia G exprima o anumita insusire esentiala, un atribut al populatiei in raport cu variabila X. Aceasta functie se numeste functie determinanta.

Prin definitie, valoarea medie a variabilei X este parametrul care lasa invarianta functia determinanta, adica:

. (2.0)

Aceasta egalitate se intalneste sub denumirea de relatia lui BOIARSKI-KISINI. In functie de forma analitica a functiei G, din relatia (2.0) se deduce expresia analitica (indicatorul) de calcul a valorii medii .

Determinarea, pe aceasta cale, a valorii medii , este destul de anevoioasa. Utilizarea acesteia presupune stabilirea continutului (semnificatiei) si a formei analitice a functiei determinante G, pentru fiecare caz in parte. Dar, valoarea medie poate fi definita ca un raport a doua marimi din care se deduce aceeasi expresie pentru ca si din (2.0).

Exista, asadar, doua modalitati echivalente de definire a valorii medii, criteriul relatiei determinante a lui Boiarski-Kisini si criteriul raportului, ultima fiind mai accesibila. Criteriul raportului presupune raportarea volumului fenomenului cercetat la volumul populatiei. Acesta presupune cuantificarea volumului fenomenului in functie de natura lui. Pentru a exemplifica cele prezentate mai sus, se considera populatia familiilor dintr-o localitate, cercetata in raport cu numarul de copii. Datele rezultate din observare se prezinta ca o serie de repartitie de forma:

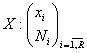
In acest caz, functia determinanta are urmatoarea forma:

semnificand numarul total de copii din localitatea respectiva. Pentru a gasi numarul mediu de copii pe familie se particularizeaza relatia (2.0) dupa cum urmeaza

de unde rezulta:

La acelasi rezultat se putea ajunge pornind de la faptul ca numarul mediu de copii pe familie se poate exprima ca un raport intre numarul total de copii si numarul de familii din localitatea respectiva, adica:

(2.1)

In acest exemplu, fenomenul fiind de natura demografica, volumul acestuia se cuantifica prin numarul total de copii la nivelul populatiei statistice considerate. Aceasta este in directa concordanta cu natura si semnificatia variabilei in raport cu care se face cercetarea statistica.

Cunoasterea "naturii" parametrului valoare medie, conduce la o definitie mai completa si plina de semnificatie.

Pentru a intelege semnificatia valorii medii , trebuie subliniat faptul ca, in general, variatia unui fenomen, de orice natura, si in particular variatia unei variabile X in raport cu care este cercetata o populatie, este determinata de actiunea simultana a doua categorii de factori: factori esentiali si factori neesentiali.

In categoria factorilor esentiali intra acei factori care actioneaza asupra tuturor unitatilor populatiei in mod continuu si in acelasi sens, determinand, in principal, nivelul de dezvoltare a variabilei pentru fiecare unitate componenta din populatie.

Factorii esentiali se conjuga in actiunea lor cu factorii neesentiali, care, in general, au un caracter aleator, sunt numerosi si neuniform raspanditi printre unitatile populatiei.

Fiecare din factorii considerati neesentiali actioneaza numai asupra unui anumit numar de unitati din populatie. Ca urmare, acestia pot contribiu fie la cresterea nivelului variabilei (pentru unele unitati din populatie), fie la scaderea nivelului variabilei (pentru alte unitati din populatie).

La randul lor factorii esentiali nu actioneaza cu aceeasi intensitate asupra tuturor unitatilor din cadrul populatie considerate, determinand, in acest fel, variatia neuniforma a variabilei respective in cadrul populatiei.

In consens cu cele subliniate mai sus, se poate afirma ca parametrul valoarea medie a unei serii statistice care are la baza variabila X, constituie acel nivel pe care l-ar putea inregistra variabila in cadrul populatiei cercetate in conditiile in care factorii neesentiali nu s-ar fi manifestat, iar factorii esentiali ar fi actionat asupra unitatilor din populatie cu aceeasi intensitate.

Parametrul valoarea medie, calculat pentru o serie statistica, pune in evidenta ceea ce este comun, general si esential sub aspectul nivelului de dezvoltare al variabilei, in raport cu care este studiata o populatie.

In raport cu natura variabilei ce sta la baza seriei, cat si a formei de prezentare a indicatorilor cu care aceasta este construita, exista mai multe posibilitati de calcul a valorii medii.

Functia determinata G, sub forma sa cea mai generala, are urmatoarea expresie analitica:

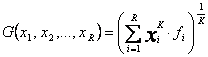(2.2)

Pentru diverse valori ale lui k, in stricta concordanta cu continutul si semnificatia functiei G, se intalnesc mai multe tipuri de medii:

media armonica (k = -1);

media aritmetica (k = 1);

media patratica (k = 2);

media cubica (k = 3);

media de ordinul k in general.

In caz concret, valoarea medie reala este aceea care se obtine prin indicatorul (mediu) rezultat fie prin aplicarea criteriului relatiei determinante, fie criteriului raportului.

Modalitati de calcul a valorii medii

1. Media aritmetica

Acesta este indicatorul cel mai utilizat in calculul parametrului valoarea medie a unei serii statistice, asa cum rezulta din practica statistica.

Se considera acum doua serii statistice de repartitie, una formata din frecvente absolute, iar cealalta din frecvente relative:

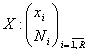(2.3)

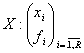(2.4)

Media aritmetica pt cele doua serii se calculeaza astfel:

Daca seria este de intevale, construita cu frecvente absolute avem:

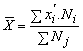
Fie o serie de repartitie, care are la baza o variabila continua X, respectiv,

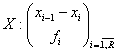
Folosind notatiile:

unde reprezinta mijlocul intervalului "i", obtinem relatia:

Relatia ne arata ca media aritmetica a unei serii de intervale se reduce la media aritmetica a unei serii discrete in care clasele sunt reprezentate prin mijloacele intervalelor de variatie.

2. Media armonica

Se considera o serie de forma:

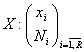(2.5)

In cazul unei serii discrete de forma (2.5), media armonica notata cu se defineste prin:

(2.6)

numita si formula mediei armonice ponderate.

Daca ponderile sunt egale intre ele, adica N₁=N₂=.=N_R=N^*, atunci relatia (2.6) devine:

(2.7)

care reprezinta formula mediei armonice simple.

In cazul unei serii care are la baza o variabila continua X, respectiv,

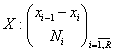
procedand ca la media aritmetica, pentru media armonica rezulta:

(2.8)

unde x_i^' reprezinta mijlocul intervalului "i", .

Si in acest caz, daca ponderile sunt egale, se obtine relatia de calcul a mediei armonice simple, de forma:

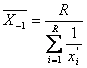
3. Media geometrica

Pentru o serie care are la baza variabila discreta X, formata cu frecvente absolute, media geometrica notata cu (sau ) este definita prin expresia:

(2.9)

Din (2.9), pentru media geometrica ponderata exprimata cu frecvente relative se deduce:

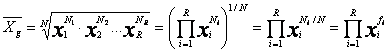(2.10)

Daca variabila X, de la baza seriei este de variatie continua, atunci relatiile de calcul pentru diversele variante de medie geometrica, raman variabile cu singura modificare ca valorile x_i, , se inlocuiesc cu mijloacele intervalelor de variatie, calculate conform formulei:

(2.11)

B. Valoarea mediana

Valoarea mediana, notata cu este acea valoare a variabilei cantitative X care imparte repartitia in doua parti egale, respectiv:

sau (2.12)

Calculul valorii mediane se face diferentiat, dupa cum seria are la baza o variabila discreta sau continua.

Pentru o repartitie discreta, calculul medianei nu implica probleme deosebite si nici un volum mare de calcule.

Se considera o repartitie cu frecvente absolute:

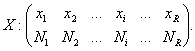(2.13)

In calculul valorii mediane a unei serii discrete, pot aparea doua situatii:

a) volumul N al populatiei este un numar impar;

b) volumul N al populatiei este un numar par.

In ambele cazuri, calculul medianei presupune, in prima faza, determinarea rangului medianei, notat cu , conform urmatoarei relatii:

(2.14)

a) Daca volumul populatiei N este un numar impar, rangul medianei este un numar zecimal a carui parte intreaga indica numarul de unitati din populatie pentru care variabila X a inregistrat valori mai mici ca mediana. Ca urmare, trebuie sa fie valoarea imediat urmatoare celei de rang adica:

(2.15)

b) Daca volumul populatiei este un numar par, rangul medianei este un numar intreg si ca urmare la mijlocul seriei nu se mai afla o valoare a variabilei X cu care sa coincida mediana ci se gasesc doua valori, mediana calculandu-se in acest caz ca media aritmetica a acestora. Relatia de calcul a medianei, in acest caz, este:

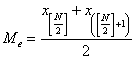(2.16)

Pentru o repartitie continua, calculul valorii mediane presupune verificarea egalitatii (2.12) si ca urmare, trebuie cunoscuta densitatea de repartitie f(x). Determinarea functiei f(x) implica un volum mare de calcule si deci, din acest motiv, in activitatea practica f(x) este aproximat. Acest lucru va conduce la o expresie aproximativa de calcul a valorii mediane, care necesita un volum redus de calcule.

Pentru acesta se considera o repartitie continua in raport cu variabila X, si anume:

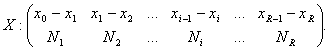(2.17)

unde intervalele x_i-1-x_i, pot fi de lungime egala sau neegala. Calcularea rangului medianei va permite stabilirea intervalului in care se afla valoarea mediana, interval numit si interval median. Se cumuleaza frecventele absolute din aproape in aproape pana ce este indeplinita inegalitatea:

Ultima frecventa N_i cumulata, ne permite sa indicam intervalul median .

Formula aproximativa de calcul a medianei:

(2.18)

- limita inferioara a intervalului median;

- frecventa absoluta a intervalului median;

- lungimea intervalului median,

C. Valoare modala

Valoarea modala M_o(X) a unei repartitii reprezinta aceea valoare a variabilei X careia ii corespunde frecventa cea mai mare.

Acest parametru se mai numeste modul, valoare dominanta, sau moda se noteaza cu M_o.

Mod de calcul

a)          Pentru o serie de repartitie discreta, data sub forma

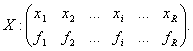(2.19)

valoarea modala se citeste direct din serie, nefiind nevoie de nici o tehnica sau formula de calcul. In cazul acestui tip de serie, valoarea modala va fi acea valoare a variabilei X pentru care frecventa este cea mai mare.

b) Pentru serii de repartitie continue, respectiv:

(2.20)

Modala nu poate fi determinata direct.

Intervalul caruia ii corespunde frecventa cea mai mare, se numeste intervalul modal si va contine modala. Sa presupunem ca intervalul modal este x_i-1-x_i.

Formula de calcul a modalei:

(2.21)

unde:

M_o - reprezinta valoarea modala;

x_Mo - reprezinta limita inferioara a intervalului modal;

- reprezinta diferenta dintre frecventa intervalului modal si frecventa intervalului precedent;

- reprezinta diferenta dintre frecventa intervalului modal si frecventa intervalului urmator;

l_Mo - reprezinta lungimea intervalului modal.

O serie poate avea o singura valoare modala, caz in care seria se numeste unimodala. Daca o serie are mai multe valori modale, atunci se numeste plurimodala. O serie plurimodala evidentiaza faptul ca populatia in cauza este neomogena. Calculul valorii modale, in asemenea cazuri, presupune o delimitare mai riguroasa a obiectului observarii cat si a populatiei care urmeaza sa fie studiata. O alta cale, care poate duce la eliminarea unui asemenea neajuns, o constituie comasarea a doua cate doua sau trei cate trei intervale etc., pana se ajunge la o serie unimodala.

In cazul unei serii simetrice valoarea modala coincide cu valoarea medie si cu mediana.

Pentru serii usor asimetrice, K. Pearson a stabilit urmatoarea relatie intre cei trei parametri:

unde este media aritmetica a variabilei X.

Calculul valorii modale reprezinta un deosebit interes pentru activitatea practica. Avand in vedere ca semnificatia acestui parametru - indica acea valoare a variabilei inregistrata de cele mai multe unitati din populatie - se poate afla: ora la care sunt solicitate cele mai multe convorbiri telefonice, ora de varf privind transportul in comun, marimea cea mai solicitata la incaltaminte etc.

Daca valoarea modala este identica cu valoarea medie, atunci se poate afirma ca valoarea medie se bucura de o mai mare reprezentativitate.

Daca, in plus, avem , tinand seama ca valoarea mediana nu este influentata de valorile extreme ale variabilei, se poate afirma ca mediana reprezinta un grad de reprezentativitate mai mare decat valoarea medie.