REZOLVAREA PROBLEMELOR GEODEZICE PRIN INTERMEDIUL TRIUNGHIURILOR ELIPSOIDICE MICI

REZOLVAREA PROBLEMELOR GEODEZICE PRIN INTERMEDIUL TRIUNGHIURILOR ELIPSOIDICE MICI

In triangulatia de ordin superior, figurile geometrice ale triangulatiei geodezice in cadrul carora s-au facut determinari de unghiuri si distante pe suprafata fizica a Pamantului, sunt transpuse si prelucrate pe elipsoidul de referinta. In scop didactic vom alege triunghiurile elipsoidice. Acestea au lungimile laturilor mici, de pana la 60 km astfel incat, in cadrul unora dintre rezolvari, suprafata elipsoidului poate sa fie aproximata cu cea a sferei de raza medie, situatie in care tratam problemele pentru triunghiuri sferice, determinarea formulelor de calcul pentru prelucrarea datelor din masuratori se va face aplicand formulele de trigonometrie sferica.

1. Excesul sferic al unui triunghi elipsoidic mic, ε

Suma unghiurilor intr-un triunghi elipsoidic mic asimilat unui triunghi sferic, chiar si atunci cand o presupunem neafectata de erori este mai mare decat 200^G. Diferenta pana la 200^G se numeste exces sferic notat cu ε:

Intre unghiurile masurate si reduse la suprafata elipsoidului de referinta, si unghiurile compensate exista relatiile cunoscute:

; ;

si dupa cum stim, suma acestor corectii este egala si cu semn contrar cu neanchiderea:

si in consecinta, se poate observa ca suma unghiurilor necompensate dintr-un triunghi si deci .

In cazul in care am lucra pe triunghiuri izolate s-ar putea considera corectiile ca fiind egale intre ele si compensa in urmatorul mod:

In cazul compensarii in retelele de triangulatie prin metoda celor mai mici patrate, nu se adopta insa o astfel de rezolvare. In ambele situatii, pentru a putea intra in compensare trebuie sa determinam o formula de calcul pentru excesul sferic, notat cu ε.

Consideram figura de mai jos in cadrul careia reprezentam pe suprafata sferei medii, triunghiul ABC, ale carui unghiuri au valorile a b g si a carui suprafata o notam cu F.

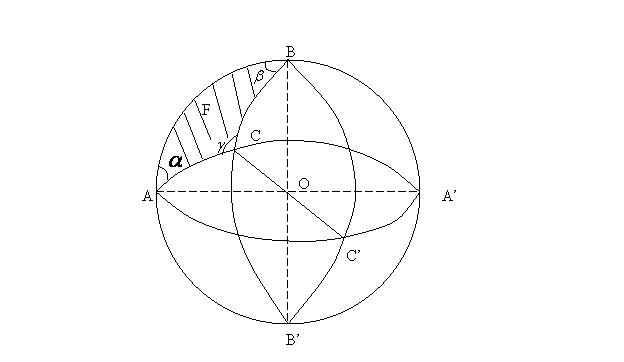
fig. 1.a

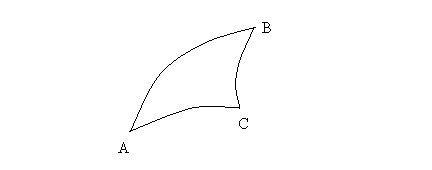
fig. 1.b

Conform desenului, putem exprima, in functie de suprafata F a triunghiului sferic ABC, suprafetele fusurilor ce il contin si pe care le vom nota (),,

()=F+BCA'

=F+ACB'

=F + ABC' = F + A'B'C

Insumand aceste egalitati obtinem:

2(F + ·R²) (1)

unde BCA', ACB' si F + A'B'C formeaza suprafata ariei semisferei care este egala cu 2··R².

Dar suprafata acestor fuse se mai poate exprima si astfel:

=

=

=

Insumand aceste egalitati obtinem:

++= (2)

Egaland relatiile (1) si (2), obtinem:

=2(F +R²)

deoarece

Pentru domeniul geodezic se poate aproxima suprafata triunghiului sferic F, calculabila cu una dintre relatiile::

F = ; F = F = cu suprafata unui triunghi plan notat cu F', calculabila cu una dintre relatiile de mai jos, in cadrul carora cu a¢ b¢ g¢ am notat valorile unghiurilor triunghiului plan corespunzator:

F' =

Excesul sferic al triunghiului are valori foarte mici, de ordinul secundelor centezimale, si se calculeaza cu formula:

Expresia se numeste factorul excesului sferic si este constanta pentru latitudinea data a triunghiului sferic, calculabila in functie de aceasta si grupata in tabelele elipsoidului astfel incat excesul sferic

In cazul in care laturile triunghiului depasesc 60 km (distante geodezice medii), excesul sferic se calculeaza cu formula:

unde cu m² am notat:

iar cu F' = aria triunghiului plan.

2. Rezolvarea triunghiurilor elipsoidice mici cu teorema Legendre

Pentru distante geodezice mici, sub 60 km, problema se rezolva prin inlocuirea suprafetei elipsoidului cu suprafata sferei de raza medie Gauss, obtinandu-se triunghiuri sferice in cadrul carora se vor aplica formule de triangulatie sferica.

In anul 1787 Legendre a imaginat urmatoarea situatie: avem un triunghi sferic ABC, cu suprafata F, careia ii cunoastem unghiurile din varfuri (a b si g) si o latura, de exemplu a (ce se mai numeste si baza geodezica) si de asemenea ne propunem sa-i calculam lungimile laturilor b si c. Adoptam un triunghi plan auxiliar A¢B¢C¢ cu suprafata F¢ ale carui unghiuri din varfuri difera ca marime de cele anterioare dar ale carui laturi sunt valoric egale cu primele. Prin rezolvarea celor doua triunghiuri vom determina expresia diferentei dintre unghiurile celor doua triunghiuri..

Aplicand teorema cosinusului in cadrul figurii nr. 4.2.a, obtinem:

de unde extragem:

In continuare se dezvolta in serie functiile trigonometrice pana la ordinul IV inclusiv:

; ;

;

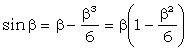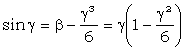
Se calculeaza numaratorul si numitorul expresiei:

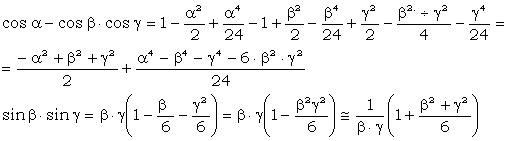
se inlocuiesc in formula lui cos A, se efectueaza calculele si rezulta:

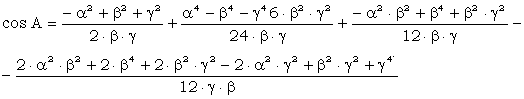
In cadrul acestei formule se inlocuiesc expresiile unghiurilor:

; ;

obtinandu-se:

Lucrand in triunghiul plan, figura nr. 4.2,b, aplicand teorema Pitagora generalizata:

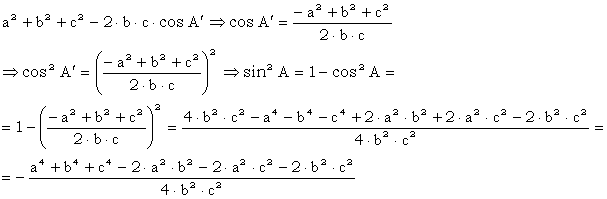
Comparand cele doua relatii rezulta:

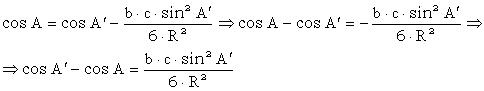
Consideram aceasta expresie ca fiind de forma: A = A¢ + (A - A¢) unde diferenta din paranteza este, cantitativ, foarte mica, suportand o dezvoltare in serie:

Diferenta (A - A¢)^rad este o cantitate mica ce se transforma in secunde sexagesimale (in geodezia elipsoidala se lucreaza in grade sexagesimale deoarece coordonatele initiale se determina din cele astronomo - geodezice):

Procedandu-se in mod similar pentru celelalte doua unghiuri, se obtine:

Relatiile enunta teorema lui Legendre care spune ca "unghiurile unui triunghi plan sunt mai mici decat cele ale triunghiului sferic corespunzator cu o treime din valoarea excesului sferic".

2. Rezolvarea triunghiurilor elipsoidice mici cu teorema aditamentelor

Pentru distante geodezice mici, sub 60 km, problema se rezolva prin inlocuirea suprafetei elipsoidului cu suprafata sferei de raza medie Gauss, obtinandu-se triunghiuri sferice in cadrul carora se vor aplica formule de triangulatie sferica.

In anul 1810 Soldner a imaginat urmatoarea situatie: avem un triunghi sferic ABC, cu suprafata F, careia ii cunoastem unghiurile din varfuri (a b si g) si o latura, a, si de asemenea ne propunem sa-i calculam lungimile laturilor b si c. Adoptam un triunghi plan auxiliar ABC cu suprafata F¢ ale carui unghiuri din varfuri sunt valoric egale cu primele dar ale carui laturi (a¢, b¢, c¢) difera ca marime de cele anterioare. Prin rezolvarea celor doua triunghiuri vom determina expresia diferentei dintre unghiurile celor doua triunghiuri..

Aplicand teorema sinusului in cadrul figurii nr. 4.a, obtinem:

Se dezvolta in serie functiile trigonometrice, pana la ordinul IV inclusiv:

;

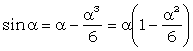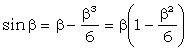
si se inlocuiesc in formula, tinand apoi seama de expresiile: ; ;

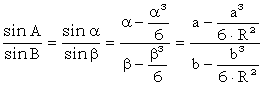
Se aplica si triunghiul plan teorema sinusurilor:

Egaland cele doua rezultate se obtine:

; si in consecinta:

Daca notam cu s latura unui triunghi sferic si cu s¢ latura unui triunghi plan, constatam marimea A_s cu care difera valoric acestea si o denumim aditament liniar: