O clasificare a marimilor electrice

a) Dupa modul de obtinere al energiei de masurare:

Marimi active: sunt acele marimi care au asociata o energie, din care o parte poate fi utilizata în procesul de masurare. Raportul între energia totala, pe care o poseda marimea respectiva si energia folosita pentru masurare trebuie sa fie cât mai mare, astfel încât sa nu se afecteze valoarea marimii masurate. Exemplu de marimi active: temperatura, tensiunea electrica, intensitatea curentului electric.

Marimi pasive: sunt acele marimi care nu poseda o energie proprie liberabila. Pentru masurarea lor este necesar sa se recurga la o sursa de energie auxiliara. Exemple de marimi pasive: masa, rezistenta, capacitatea, inductivitatea.

b) Dupa aspectul dimensional-spatial:

Marimi scalare: complet determinate printr-un singur numar.

Marimi vectoriale: caracterizate prin: modul(intensitate), directie si sens.

Marimi tensoriale: Tensorul este o marime atasata unui punct din spatiu si care este alcatuita dintr-un ansamblu ordonat de componente scalare. Exemplu: tensorul eforturilor ce apar într-un corp solid deformat.

c) Dupa modul de variatie în timp:

Fig.1.1. Clasificarea marimilor electrice dupa modul de variatie în timp

Marimea constanta: este acea marime care nu îsi modifica valoarea în timp, având doar doi parametrii, amplitudine si polaritate.

Marimea determinista: este acea marime a carei evolutie în timp este previzibila, putând fi descrisa printr-o functie matematica si la care imprevizibilul intervine într-o mica masura.

Marimea aleatoare: prezinta variatii neprevizibile, valorile pe care le ia în diverse momente de timp fiind întâmplatoare. Aceste marimi nu pot fi caracterizate decât în sens probabilistic cu ajutorul metodelor statistice.

Valoarea medie (componenta continua) a unei marimi aleatoare, într-un anumit interval de timp t₁-t₂ este data de relatia (1.2), iar valoarea efectiva de relatia (1.3).

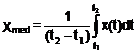(1.2)

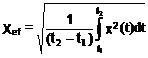(1.3)

unde t₂-t₁ reprezinta timpul de integrare sau timpul de masura.

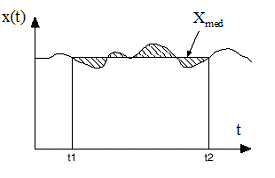
Fig.1.2. Marime aleatoare

Marimea periodica: are proprietatea ca valorile pe care le ia la anumite momente, se repeta dupa intervale egale de timp. Astfel pentru o marime periodica, valoarea sa instantanee (momentana), x(t),satisface relatia:

(1.4) x(t)=x(t+kT) (1.1)

unde T este perioada si f=1/T este frecventa

Valoarea medie a unei marimi periodice este:

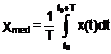(1.5)

Un alt parametru utilizat pentru caracterizarea marimilor periodice este valoarea efectiva:

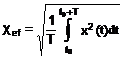(1.6)

Aplicatia 1.1.

Sa se determine valoarea medie si valoarea efectiva a semnalului periodic din Fig.1.3.

   

Fig.1.3. Semnal dreptungiular

Marimea alternativa: este acea marime periodica a carei valoare medie pe perioada este nula.

Cele mai întâlnite marimi alternative în domeniul electric sunt prezentate în Fig.1.4.

Fig.1.4. Principalele forme de unda alternative

Fata de tensiunea si de curentul continuu, ale caror valori în timp sunt în general stabile, tensiunea alternativa alterneaza în polaritate (Fig.1.4), iar curentul alternativ alterneaza în directie (Fig.1.5).

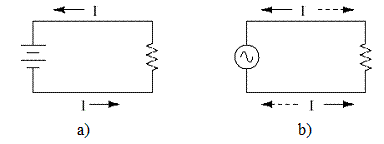
Fig.1.5. Curent continuu (a) si curent alternativ (b)

O modalitate de a exprima intensitatea sau amplitudinea unei marimi alternative consta în masurarea valorii de vârf sau a valorii vârf la vârf (Fig.1.6).

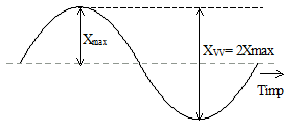
Fig.1.6. Valoarea maxima si valoarea vârf la vârf a unei marimi alternative

Din pacate fiecare dintre aceste valori ne pot însela daca comparam doua tipuri diferite de unda. Astfel, o tensiune dreptunghiulara cu valoarea de vârf de 10V este clar o valoare mai mare în timp decât valoarea de vârf de 10V a unei tensiuni triunghiulare, efectul acestor doua tensiuni ce alimenteaza aceiasi sarcina fiind diferit (Fig.1.7).

O alta valoare importanta, ce ofera informatii referitoare la puterea electrica, a unei marimi electrice este valoarea efectiva sau valoare RMS (Root Mean Square). Valoarea efectiva a unei tensiuni electrice alternative este egala cu valoarea tensiunii continue care determina pe o aceiasi sarcina, aceiasi putere electrica. În cele doua circuite din Fig.1.8, cele doua surse de tensiune, una alternativa si una continua, determina un anumit curent prin sarcina de 2W. Reglam din sursa de curent continuu pâna se obtine aceiasi putere disipata, sub forma de caldura, ca si pe rezistenta alimentata în curent alternativ. Daca valoarea tensiunii continuee este de 10V, atunci valoarea efectiva a tensiunii alternative este tot de 10V, respectiv valoarea efectiva a curentului I_ef=10V/2W=5A.

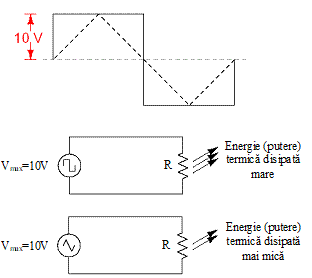
Fig.1.7. Efectul alimentarii aceleiasi sarcini cu doua tensiuni diferite, dar având aceiasi valoare maxima

Raportul dintre valoarea de vârf (maxima) si valoarea efectiva a unei marimi (semnal) electrice se numeste factor de vârf:

K_v=X_max/X_ef (1.7)

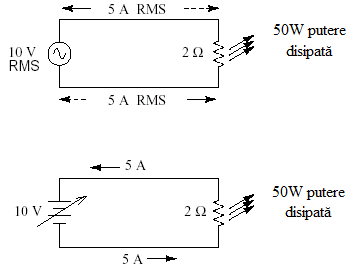
Fig.1.8. Analogie între valorile efective si valorile continui ale tensiunii si curentului electric

Marimea pulsatorie: este acea marime periodica a carei valoare instantanee nu-si schimba semnul (Fig.1.9).

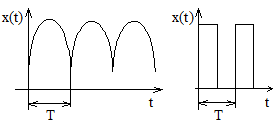
Fig.1.9 Marimi pulsatorii

Marimea neperiodica (aperiodica): nu mai este caracterizata de relatia (1.4). Aceasta marime evolueaza în timp dupa legi predeterminate, dar valorile pe care le ia nu au un caracter periodic. Exemplu de astfel de marimi: parabole, hiperbole, exponentiale e.t.c.

Marimea sinusoidala

Este o marime alternativa data de relatia:

x(t)=X_msin(t+j (1.8)

unde: x(t) – valoarea momentana (instantanee);

X_m – valoarea maxima (de vârf);

wt – faza;

j - faza initiala;

w=2pf – pulsatia;

f = 1/T – frecventa;

T = 2p w - perioada.

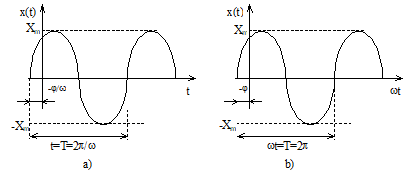
Fig. 1.10. Reprezentarea în timp (a) si respectiv în faza (b), a unei marimi sinusoidale

Deci practic o marime alternativa sinusoidala este definita prin 3 parametrii: amplitudine, frecventa si faza.

Se observa ca valoarea medie pe o perioada (componenta continua) a marimii sinusoidale este nula, iar valoarea efectiva este data de relatia:

X_ef = (1.8)

În tabelul 1.1 sunt prezentate principalele marimi (semnale) electrice si parametrii acestora.

Tabelul 1.1