Rezistente la transfer de masa

Rezistente la transfer de masa

1.Bazele analitice ale transferului de masa

a.      Conditiile fizice de transfer de masa

b.     

In aprecierea permeabilitati la transfer de masa a materialelor utilizate pentru anvelope, trebuie sa se tina seama de doua fenomene fizice si anume:

transferul de masa sub forma de vapori, se datoreaza diferentelor de presiuni partiale a vaporilor de apa din aerul celor doua medii despartite;

transferul de masa sub forma lichida (prin capilaritate), intre suprafetele materialului de constructie relativa.

Rezulta ca in acelasi timp, printr-un element de constructie exista doua componente de transfer de masa, pentru care exista diferente de potential diferite, sensul transferului fiind important si determinabil pe baza starii fizice locale a parametrilor de stare ai aerului din interior si exterior.

Pentru aplicarea acestor fenomene de transfer, vom conveni sa notam fluxurile unitare de masa astfel:

q_v - fluxul unitar de masa sub forma de vapori, care se transforma datorita diferentelor de presiuni partiale "s_pv";

q_e - fluxul unitar de masa sub forma lichida, transmis prin capilaritate, datorita diferentelor de unitati relative "Dj

Stabilirea sensului de transfer se va face considerand un perete plan delimitand aer exterior in conditii climatice de iarna si de vara.

In perioada de iarna, fluxul termic va avea directia I E, deoarece t_i>t_e; fluxul de masa sub forma de vapori va avea aceeasi directie p_vi>p_ve,     in timp ce directia fluxului de masa transmis prin capilaritate va fi opus primelor doua deoarece j_E>j_I (80%>50%).

In perioada de vara sensurile primelor doua componente (q si q_v) se schimba, fiind de la exterior la interior, iar a componentei "q_e" va fi tot in opozitie cu primele doua (j_I>j_E

Aceste observatii fenomenologice sunt foarte importante, deoarece vaporii de apa pot intalni in calea lor conditii fizice de condensare, revenind la interior gratie componentei "q_e", putand crea suprafete cu condens Mai dificila situatie este aceea cand vaporii de apa ce condenseaza in structura pot ingheta. Fenomenul de inghet si dezghet poate avea ca efect distrugerea materialului.

Pe de alta parte, in procesele de transfer de masa, trebuie sa se tina seama de proprietatile si starea de umiditate a materialelor, din care punct de vedere acestea prezinta urmatoarele stari de umiditate:

umiditate libera, formata prin condensarea vaporilor de apa in interiorul materialului, prin contactul direct al materialelor cu apa sub forma lichida;

umiditate de sorbtie, formata prin sorbtia umezelii din aer, adica prin contactul materialului cu apa sub forma de vapori.

Marimea acesteia creste cu umiditatea relativa a aerului inconjurator si descreste cu temperatura.

Din reprezentarea alaturata a izotermelor de sorbtie, rezulta ca exista 3 zone caracterizate astfel:

zona 1 - pe suprafata porilor si a capilarelor materialelor se formeaza sub actiunea fortelor moleculare, o pelicula subtire dintr-un strat monomolecular;

zona 2 - sorbtia vaporilor de apa se extinde in grosimea materialului si pe suprafata porilor se formeaza un strat

polimolecular. Deplasarea treptata a umezelii in material are loc incet in timp si reprezinta fenomenul difuziei vaporilor de apa prin peretii porosi;

zona 3 - la absorbtie se adauga fenomenul de condensatie capilara. In acest stadiu, umezeala se deplaseaza atat sub forma de vapori cat si sub forma lichida, din care cauza fenomenul nu mai poate fi bine cuprins in modelele de calcul existente.

Modelele de calcule vor fi prezentate si dezvoltate iau in considerare ipoteza materialelor cu o capilaritate foarte redusa.

Pe de alta parte, Eichler, clasifica materialele de constructie dupa raportul dintre fluxul de masa si luxul de caldura.

Din clasificarea facuta se constata ca zidaria din caramida are un raport maxim intre cele doua componente, motiv pentru care acesta nu a ridicat probleme higrotermice de-a lungul timpului.

Straturile neomogene aparute ulterior a creat si creeaza probleme diferentelor de comportament higrotermice.

b. Parametrii termofizici ai transferului de masa

Materialele de constructii opun o anumita rezistenta la transferul de masa, in functie de de structura lor si de continutul de umiditate. De aceea, in alcatuirea elementelor de constructii (pereti, plansee, terase etc.) trebuie sa se tina seama de natura materialelor, de modul cum se comporta ele la transferul de masa.

Relatiile generale ale campului de umiditate si ale fluxului de vapori dintr-un element de constructie se deduc pe baza ecuatiei difuziunii, cunoscuta ca legea lui Fick.

div.grad C;

in care "C" este concentratia vaporilor de apa iar "Kd" coeficientul de difuzie al vaporilor.

Fluxul elementar de umiditate este proportional cu gradientul de concentratie, dupa cum fluxul elementar de caldura, in cazul conductiei, este proportional cu gradientul de temperatura.

Astfel, pentru transferul de masa se poate scrie expresia fluxului unitar:

Pe baza legii lui Fick care arata ca difuziunea este dependenta de campul de concentratie, fluxul unitar de vapori se poate exprima si sub forma:

q_v=bDC=b(C₁-C₂); Kg/m²

in care "b" este coeficientul de transfer superficial de masa, in m/s; iar C₁, C₂ concentratiile vaporilor de apa intre planurile de transfer.

Expresia luxului de masa dupa Dalton, functie de diferenta vaporilor de apa are forma:

q_v=b(p_v1-p_v2);    (p_v1>p_v2); [Kg/m²]

De asemenea Lewis a exprimat aceeasi marime functie de diferenta continuturilor de umiditate:

g_v=s(x₁-x₂); (x₁>x₂);

Intre coeficientii de transfer de masa se pot stabili, aplicand legea gazelor perfecte, urmatoarele relatii:

s bg b=b; b=;

Elementele de constructie sunt in general pereti plani, cu fete paralele, avand pe de o parte doua din dimensiuni mai mari, in raport cu cea de-a treia, deci efectele marginale pot fi neglijabile, iar pe de alta parte, toate suprafetele peretilor sunt izoterme, ceea ce face ca variatia campului de temperatura sa aiba loc numai pe directia normala pe suprafetele izoterme. In acest caz, ecuatia diferentiala a conductiei devine:

care prin, integrare, cu conditii la limita de speta intaia si a treia, conduce la expresia campului de temperatura:

precum si expresia fluxului unitar de caldura:

In mod analog se poate scrie pentru campul de concentratie, tinand cont de legea gazelor perfecte:

sau

In cazul in care se admite aproximatia:

se poate scrie:

Daca se ia in consideratie expresia fluxului de masa dupa Dalton si Fick, precum si legatura dintre coeficienti de transfer b si b, rezulta:

Daca definim rezistenta la transfer termic de masa ca fiind analoaga transferului de caldura in regim stationar putem scrie:

; (m²hmmHg/g)

in care: R_vi=; R_ve R_vn=

cu m - coeficient de transfer de masa, b si b coeficient de transfer superficial

; [g/m h mmHg]

2.Analiza zonelor de condensare in structuri

Se va considera o structura neomogena pentru care se va stabili conditiile de condensare a vaporilor de apa, in conditii termice de iarna.

Fiecare element omogen este caracterizat prin marimile fizice specifice: l si m; pe de alta parte vaporii de apa sunt caracterizati de presiuni partiale (p_v) si de saturatie (p_s), care la randul lor depind de starea termica locala.

Evident ca p_s>p_v in conditii fizice normale, pe cand conditiile de egalitate creeaza premizele condensarii vaporilor de apa pe o suprafata sau zona structurala.

Analogia fizica demonstrata anterior ne va permite ca in cadrul unei structuri neomogene, sa reprezentam grafic variatiile de presiuni partiale, luand pe abscisa scara rezistentelor la transfer de masa conductiv (R_v).

Asa cum s-a aratat, pentru o structura oarecare vom putea scrie o expresie corespunzatoare conservarii fluxului de masa:

; [g/m²h]

S-a aratat deja ca R_vi=1/b_i si R_ve=1/b_e, reprezinta rezistentele la transfer superficial de masa, ale caror valori numerice fiind foarte mici, se vor putea neglija in aplicatiile care urmeaza.

Cu aceste simplificari, expresia de mai sus va putea fi scrisa sub forma dependentei de rezistenta la transfer conductor de masa:

g_v====; [g/m²h]

Procedand ca si in cazul campului de temperatura, vom obtine expresia campului de presiuni partiale ale vaporilor de apa (p_vx).

Pentru suprafata, determinarea presiunii partiale se face functie de umiditatea relativa "j_i", cunoscuta din conditiile de confort si presiune de saturatie (p_si), corespunzatoare acestei stari [I=I(j,t)]:

; si respectiv

sau cu ajutorul diagramei i-x.

Pentru celelalte suprafete vom putea scrie:

; [mmHg]

; [mmHg]

; [mmHg]

Reprezentarea grafica a presiunilor partiale si de saturatie ne va permite sa analizam situatiile in care structurile au un prost comportament la transferul de masa. Daca in toata structura intre cele doua valori exista o diferenta semnificativa, se poate afirma ca structura va avea un bun comportament la transferul de vapori.

a.Cazul condensarii vaporilor de apa pe o suprafata

Desigur nu vom lua in discutie cazul condensarii pe o suprafata interioara, deoarece conditia de necondensare a fost impusa structurii prin rezistenta termica minima necesara.

Punem in discutie, acum condensarea pe o suprafata din interiorul structurii. Conditiile fizice ce trebuie indeplinite pot fi scrise fie sub forma p_vx=p_vs, fie conditiile de temperatura de condens t_x=t_t

Acceptand reprezentarea grafica a presiunilor functie de rezistenta la transfer, variatia este liniara.

In ambele cazuri putem pune problema determinarii fluxului de masa condensat:

; [g/m²h]

Se observa ca pe suprafata de condensare p_v =p_s

In prezentarea grafica alaturata s-a admis ca pe suprafata stratulzui 4, cele doua presiuni devin egale, putandu-se asista la un fenomen de condensare pe inteagra suprafata.

Se pot presupune doua situatii: una in care condensarea este partiala si cea de a doua in care este totala.

Pe de alta parte, conditiil4e termice locale pot permite inghetarea acestor vapori, caz in care returul acestora catre suprafata de plecare, odata cu componenta lichida nu mai este posibila. Aceasta situatie termica trebuie evitata, prin modificarea rezistentelor locale, in scopul pozitivarii temperaturilor.

Pentru determinarea fluxului de masa condensat, este necesar sa se determine in prealabil timpul "t" cat dureaza condensarea.

Pentru aceasta se determina, in primul rand, de la ce temperatura exterioara va fi sub aceasta valoare.

Determinarea temperaturilor exterioare (t_i, j_i j). Apoi se determina durata in ore "t_z", functie de zona de temperaturi corespunzatoare amplasamentului.

Fluxul de masa condesat va fi dat de expresia:

G_cd=g_cd*t_z [g/m²]

Sigur ca aceasta valoare ne va permite sa apreciem daca condensarea este totala sau partiala, situatie pe care vom scrie expresia fluxului de masa intrat in structura: g_vi= sau G_vi=g_vi*t_z [g/m²].

Daca G_vi=G_cd, condensarea este totala, contrar sau partial.

Pentru a asigura o comportare buna a structurilor, este necesar ca in timpul verii masa de vapori condensata sa se poata evapora catre una dintre cele doua suprafete, pe

care avem aceeasi presiuni partiale admitand ca fereastra este deschisa.

In interiorul elementului, pe sprufata de condensare vom avea presiune de saturatie maxima deoarece j j_max

Cu aceste ipoteze vom putea scrie:

g_ev= [g/m²h]

sau

G_ev=g_ev*24*30;    [g/m²]

conditia de evaporare fiind de 30 de zile.

Cazurile multiple de aparitie a condensului pe suprafetele interioare , ne face sa credem ca pana la aparitia conditiilor favorabile de evaporare din perioada de vara, masa de vapori condensata se intoarce catre suprafata interioara si datorita temperaturilor scazute, nu se poate evapora, formand ceea ce numim "igrasia".

c.       zone de condensare

Acest caz particular reprezinta o extensie a celui studiat anterior, fapt pentru care raman valabile toate ipotezele de calcul explicitate anterior. Pentru acest caz se poate scrie:

; [g/m²]

Una din marile probleme ale condensarii o reprezinta pericolul de inghet-dezghet. Analiza acestei situatii se poate face prin incercari succesive, de fiecare data verificandu-se daca apar temperaturi de inghet sau dezghet.

3. Rezistentele optime la transferul de masa

Optimizarea rezistentelor higrotermice ale unei structuri, presupune si analiza la transfer de masa, astfel incat condensarile sa fie evitate sau protejate impotriva inghetului.

Putem totusi introduce notiunea de rezistenta optima, daca admitem ca aceasta va trebui sa evite condensarea in zone de temperatura negative si sa permita evaporarea pe timpul iernii pe suprafata interioara.

Stabilirea acestei rezistente se face din aproape in aproape, parcurgand toate fazele de verificare explicate anterior.

4. Masuri constructive specifice transferului de masa

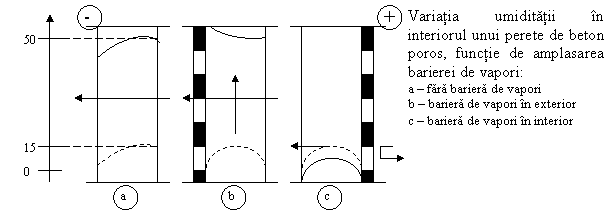
In actiunea de reducere a efectelor nefavorabile, datorate migratiei vaporilor de la interior catre exterior, un factor important il constituie bariera de vapori, compusa din materiale care, desi au grosimi reduse, opun o rezistenta mare la trecerea vaporilor.

In interiorul peretelui in starea initiala a existat o umiditate de maximum 15% din greutatea materialului. Dupa cateva luni de exploatare a acestui perete, la o incapere care avea umiditatea relativa j_i=80%, variatia umiditatii a ajuns la 50%.

Se observa ca spre exterior aceasta umiditate scade rapid, ceea ce se explica prin

capacitatea peretelui de beton usor de a elimina rapid umiditatea sau cum se spune, datorita posibilitatii de a respira.

In cazul "b" se analizeaza montajul unei bariere de vapori la exterior, caz in care se constata o crestere a umiditatii interioare.

In cazul "c", cand bariera de vapori se afla la interior, se constata o scadere a umiditatii interioare cu 5-6%.

In mod intuitiv, aceasta experienta rata avantajele amplasarii la locul potrivit a barierei de vapori si ca placajele impermeabile ale zidariei la exterior, pot da rezultate foarte proaste.

Astfel a aparut recomandarea ca bariera de vapori sa fie amplasata pe partea calda a peretelui, existand solutii ca: tapete, cartoane asfaltate etc.