Notiuni de baza privind identificarea modelelor dinamice ale proceselor

Notiuni de baza privind identificarea modelelor dinamice ale proceselor

Acest capitol prezinta principiile de baza ale identificarii miodelelor dinamice ale proceselor si principalele tipuri de algoritmi de adaptare parametrica ce intervin in metodele de identificare recursive. Apoi este analizata alegerea intrarilor pentru identificare si influenta perturbatiilor. In ultima parte se indica structura generala a metodelor de identificare recursive.

Principiile identificarii modelelor dinamice ale proceselor

Identificarea este operatia de determinarea a caracteristicilor dinamice ale procesului(sistemului), a carui cunoastere este necesara pentru proiectarea si implementarea unui sistem performant de reglare.

Figura 1 rezuma principiile generale de proiectare si calcul ale unui regulator.

Pentru a concepe si ajusta corect un regulator sunt necesare:

specificarea performantelor dorite pentru bucla de comanda /reglare;

cunoasterea modelului dinamic al procesului (numit model de comanda ) ce descrie relatia intre variatiile comenzii si variatiile iesirii;

disponibilitatea unei metode adecvate de calcul al regulatorului compatibil cu performantele specificate si caracteristicile modelului procesului;

Notiunea de model matematic al unui sistem sau fenomen este un concept fundamental. In general, exista diferite tipuri de modele, fiecare model fiind destinat unei aplicatii specifice.

Figura 1: Principiul proiectarii si calculului unui regulator.

De exemplu modelele de cunoastere(bazate pe legi fizice, chimice, etc.) permit o descriere destul de completa a sistemelor si sunt utilizate pentru simularea si modelarea proceselor. Aceste modele sunt, in general, extrem de complexe si rareori direct utilizabile in automatica. Modelele dinamice de comanda, ce dau relatia intre variatiile intrarilor unui sistem si variatiile iesirii, sunt, asa cum s-au prezentat anterior, tipuri de modele necesare pentru priectarea si ajustarea sistemelor de comanda /reglare. Desi indicatii asupra strcturii acestor modele de comanda se pot obtine pornind de la structura modelului de cunoasere, in general, este foarte dificil sa se determine valorile parametrilor semnificativi pornind de la aceste modele.

De aceea, in marea majoritate a situatiilor practice, este pusa in aplicare o metodologie de identificare directa a acestor modele dinamice(de comanda). De notat ca modelele de comanda sunt de doua tipuri:

1. Modele neparametrice

(Exemple: raspuns in frecventa la treapta, etc.)

2. Modele parametrice

(Exemple: functie de ransfer, ecuatie diferentiala sau cu difernte, etc.)

In continuare, ne intereseza identificarea modelelor dinamice parametrice discretizate adecvate proiectarii si ajustarii sistemelor numerice de comanda si reglare.

Identificarea este o tehnica experimentala pentru determinarea modelului dinamic al sistemului; ea cuprinde patru etape:

1. Achizitia intrarilor/iesirilor cu un protocol de experimentare.

2. Alegerea structurii modelului(determinarea complexitatii sale).

3. Estimarea parametrilor modelului.

4. Validarea modelului identificat(validarea structurii si a valorilor parametrilor).

O operatie de identificare completa trebuie neaparat sa contina cele patru etape indicate mai sus. Metodele specificate utilizate in fiecare etapa depin de tipul modelului cercetat (parametric sau neparametric, continuu sau discret).

Metoda de identificare clasica utilizata pentru obtinerea modelelor parametrice pornind de la modele neparametrice de tip "raspuns la treapta" este prezentata in figura 2. Aceasta metoda a fost utilizata initial pentru a obtine modele parametrice continue, apoi ea a fost extinsa pentru identificarea modelelor discrete.

Pornind de la forma raspunsului procesului la treapta, se alege un tip de model si se determina grafic parametrii modelului. Cunoscand frecventa de esantionare, se poate obtine cu ajutorul tabelelormodelul discret corespunzator.

Dezavantajele acestei metode sunt multiple:

semnalele de test au amplitudine mare(fiindrareori tolerate de instalatiile industriale);

precizia modelului obtinut este redusa;

influenta perturbatiilor este semnificativa, ele conducand cu usurinta la necesitatea schimbarii modelului ales;

nu exista posibilitatea modelarii perturbatiilor;

timpul de calcul este mare;

nu esista posibilitatea validarii modelului

Disponibilitatea unui calculator numeric permite implementare algoritmilor de estimare automata a parametrilor modelelor discrete ale proceselor. Este important de subliniat ca identificarea modelelor parametrice discrete permite (prin simulare) obtinerea unor modele neparametrice de tip "raspuns la treapta" sau "raspuns in frecventa", cu o precizie mai are decat in cazul unei abordari directe si utilizand semnale de excitatie extrem de slabe. Identificarea modelelor parametrice discrete conduce la modele de utilizare foarte generala si ofera numeroase avantaje in raport cu celelalte abordari.

Au fost dezvoltati algoritmi de identificare performanti avand o formulare recursiva adaptata problemelor de identificae in timp real si implementarii lor pe microcalculator. Faptul ca aceste metode de identificare pot lucra cu semnale de excitatie extrem de slabe constituie o calitate apreciata in practica.

Principiul estimarii parametrilor modelelor discrete este prezentat in figura 3.

Un model discret cu parametri ajustabili este implementat pe calculator. Eroarea intre iesirea procesului la momentul t, y(t), si iesirea predictata de model, ŷ(t), numita eroare de predictie, este utilizata de algoritmul de adaptare parametrica. Acesta va modifica parametrii modelului la fiecare moment de esantionare, astfel incat sa se minimizeze aceasta eroare. Intrarea este, in general, o secventa pseudo-aleatoare binara de un nivel foarte slab, generata de calculator (succesiune de impulsuri dreptunghiulare cu durata aleator variabila). Odata modelul obtinut, o validare obiectiva poate fi facuta prin teste statistice asupra erorii de predictie ε(t) si a iesirii predictate ŷ(t). testul de validare permite pentru un proces dat sa se aleaga cel mai bun model, respectiv cea mai buna structura si cel mai bun algoritmpentru estimarea parametrilor.

Calculand si reprezentand grafic raspunsul la o treapta si raspunsul in frecventa al modelului identificat, se poate determina modelul continuu(raspuns la o treapta sau raspuns in frecventa).

Aceasta abordare moderna pentru identificarea modelelor procesului elimina dezavantajele metodelor clasice mentionate anterior si ofera, de altfel, ti alte posibilitati, cum ar fi:

Figura 2: Metoda clasica de identificare

Figura 2: Principiul estimarii parametrilor unui model.

urmarirea variatiilor parametrilor procesului in timp real, permitand o reacordare a regulatoarelor in timpul functionarii;

identificarea modelelor de perturbatie;

modelare zgomotelor din captatoare in vederea eliminarii lor;

detectia si masurarea frecventelor de vibratie;

analiza spectrala a semnalelor.

Unul din elementele cheie pentru aplicarea aestei abordari pentru identificarea modelului procesului este algoritmul de adaptare parametrica (AAP), ce ajusteaza parametrii modelului de predictie plecand de la indicatiile culese de la sistem al fiecare pas de esantionare. Acest algoritm are o structura recursiva, adica noua valoare a parametrilor este egala valorii precedente plus un termen de corectie ce va depinde de ultimele masuratori.

Se defineste, in general, un vector al parametrilor in care componentele sunt diferitii parametri care trebuie identificati. Algoritmii de adaptare au structura urmatoare:

	Noua estimatie a parametrilor (vector)		Estimatia precedenta a parametrilor (vector)		Amplificarea de adaptare (matrice)		Functia de masurare (vector)		Functia de erori de predictie (scalar)

= +

Vectorul functiilor de masurare se mai numeste vector al observatiilor .

Exista algoritmi nerecursivi de identificare parametrica (ce prelucreaza in bloc fisierele cu date de intrare/iesire obtinute pe un orizont de timp). In comparatie cu aceste tehnici identificarea recursiva ofera avntajele urmatoare:

obtinerea unei estimatii a modelului pe masura ce procesul evolueaza;

compresia datelor, pentru ca algoritmii recursivi nu prelucreaza la un moment dat decat o pereche de date intrare/iesire, spre deosebire de ceilalti algoritmi ce utilizeaza ansamblul de date;

necesarul de memorie si putere de calcul sensibil diminuate;

implementarea usoara pe microcalculator;

posibilitatea de a realiza sisteme de identificare in timp real;

posibilitatea de a urmari paramatrii sistemelor variabile in timp.

Subcapitolul urmator este consacrat prezentarii principalelor tipuri de algoritmi recursivi de adaptare parametrica.

2 Algoritmi recursivi pentru identificarea parametrica

2.1 Abordare euristica

Se considera modelul discret al procesului descris prin:

y(t+1)=-a₁y(t)+b₁(t)u(t), tIN (1)

unde a₁ este un parametru cunoscut si b₁ este un parametru avand o valoare pozitiva dar necunoscuta.

Obiectivul este de identifica (estima) valoarea parametrului b₁. Modelul ce va fi identificat va avea aceeasi structura cu cel de sus. Pentru a identifica b₁, va trebui construit un model adjustabil de forma ecuatiei (1), unde b₁ va fi inlocuit prin estimatia sa B₁(t) , ce va fii modificat de un algoritm de adaptare parametrica. Efectul acestui algoritm va trebui sa se concretizeze printr-o reducere a distantei dintre iesirea reala si iesirea predictata printr-un model ajustabil.

Modelul ajustabilde predictie (a priori) va fi deci descris prin:

(t+1)=-a₁y(t)+, tIN (2)

unde B₁(t) este o estimatie a lui b₁ la momentul t. Se defineste eroarea de predictie (a priori):

ε⁰(t+1)= y(t+1)- ŷ⁰(t+1), tIN (3)

Sa examinam acum cateva situatii in functie de valorile lui b₁ si .

1. Cazul parametrului subestimat: u(t) 0 de tip treapta: . Raspunsurile procesului si modelului sunt prezentate in figura 4.

In acest caz, ε⁰ (t)>0.

Figura 4: Evolutia lui y(t) si ŷ⁰(t) in cazul subestimarii parametrului.

2. Cazul parametrului supraestimat u(t) 0 de tip treapta: .

Raspunsurile procesului si modelului sunt reprezentate in figura 5

Figura 4: Evolutia lui y(t) si ŷ⁰(t) in cazul supraestimarii parametrului.

In acest caz, ε⁰ (t)<0.

Analizand cele doua situatii, se poate propune un algoritm de adaptare parametrica de forma:

, (4)

unde f > 0 este amplificarea de adaptare. De notat ca aceasta ecuatie are forma unui integrator numeric, ceea ce garanteaza memoria algoritmului (daca ε⁰ (t+1)=0 atunci ).

Sa studiem acum evolutiile b₁(t) cu acest algoritm (prin conventie, va indica o crestere, iar -o descrestere):

Se observa ca, pentru u(t) > 0, actiunea algoritmului de adaptare parametrica este buna.

Din contra, daca se schimba semnul lui u t) (u(t) < 0). Algoritmul de adaptare parametrica face ca sa evolueze intr-un sens nedorit. Acest lucru este prezentat in figura 6. Trebuie deci modificat algoritmul dat prin ecuatia (4) pentru a tine cont de semnul lui u(t) (trebuie inversata actiunea atunci cand u(t) este negativ).

Figura 6: Evolutia lui utilizand algoritmul ecuatiei (4) pentru u(t)<0

Dar: (5)

si algoritmul de adaptare parametrica devine:

. (6)

Acest nou algoritm actioneaza intr-un sens bun asupra lui ,oricare ar fi semnul lui u(t). Se obtine:

Se pot aduce o serie de ameliorari la algoritmul de adaptare parametrica (AAP) dat prin ecuatia (6).

O prima imbunatatire se poate face prin reducerea sensibilitatii algoritmului in raport cu amplitudinea lui u(t) si a valoriiamplificarii f.

Din ecuatiile (1) ,(2), (3) se obtine:

. (7)

Altfel spus, termenul de corectie este proportional cu produsul . Este convenabil ca termenul de corectie sa fie normalizat, impartindu-l cu . Algoritmul de adaptare devine deci:

. (8)

A doua imbunatatire se refera la situatiile cand ceea ce conduce la o impartire cu 0. pentru a o evita, algoritmul din ecuatia (8) se modifica astfel:

. (9)

In ecuatia (9) se poate pune in evidenta un termen de forma ce are o inerpretare foarte interesanta. Pentru aceasta, in ecuatia (2) se inlocuieste cu si se noteaza noua iesire a modelului(model de predictie a posteriori):

. (10)

Utilizand ecuatia (9), ecuatia (10) se poate rescrie:

(11)

.

Se defineste:

, (12)

Utilizand relatiile (11) si (3) in aceasta definitie, se obtine:

. (13)

In acest context, este numita eroare de predictie a priori, pentru ca depinde de parametrii estimati la momentul t. Analog, este numita eroare de predictie a posteriori, deoarece depinde de parametrii estimati la momentul t+1, adica dupa ce algoritmulde adaptare parametrica a actionat. Ecuatia (13) da relatia dintre eroarea de predictie a priori si eroarea de predictie a posteriori. Se constata ca (egalitatea avand loc pentru f sau u nuli). Ecuatia (13) permite de asemenea sa se rescrie algoritmul de adaptare parametrica din ecuatia (9) sub forma:

, (14)

unde este dat de ecuatia (13) si ce depinde numai de parametrii estimati la momentul t.

Algoritmul gradientului

Algoritmul de adaptare parametrica a gradientului are ca obiectiv minimizarea unui criteriu patratic in functie de eroarea de predictie.

Se va considera acelasi exemplu ca in paragraful 2.1, dar, de aceasta data, cei doi parametri ai modelului procesului, a₁ si b₁, sunt necunoscuti.

Modelul discretizat al procesului se scrie:

, (15)

unde:

(16)

este vectorul parametrilor (necunoscuti) si

, (17)

este vectorul masurilor (sau al observatiilor).

Modelul de predictie ajustabil (a priori) va fi descris in acest caz prin:

, (18)

unde reprezinta predictia a priori ce depinde de valorile parametrilor estimati la momentul t si

, (19)

este vectorul parametrilor estimati.

Iesirea a posteriori a predictorului va fi data prin:

(20)

Se defineste o eroare de predictie a priori prin:

(21)

si o eroare de predictie a posteriori prin:

(22)

Se cauta un algoritm de adaptare parametrica recursiv si cu memorie. Structura unui astfel de algoritm este:

. (23)

Termenul de corectie trebuie sa depinda numai de informatiile disponibile la momentul t+1(ultima masurare y(t+1), parametrii ) si eventual un numar finit de informatii la momentele t, t-1, t-2, .,t-n). Termenul de corectie de corectie permite minimizarea la fiecare pas a criteriului:

, (24)

minimizarea efectuandu-se in raport cula momentul (t+1).

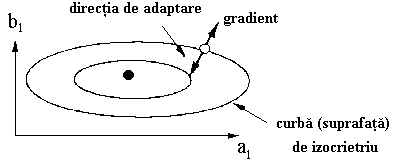
Solutia se obtine utlizand metoda gradientului. Daca se reprezinta curbele de izocriteriu (pentru care J este constant) in planul parametrilor a₁, b₁ , se obtin curbe inchise concentrice in jurul valorii minimale a criteriului corespunzatoare punctului a₁, b₁ (parametrii modelului procesului). Curbele de izocriteriu se departeaza de minim pe masura ce valoatrea lui J creste. Acest lucru este prezentat in figura 7.

Figura 7: Principiul metidei gradientului

Pentru a minimiza valoarea criteriului, se va efectua o deplasare in directia inversa gradientului curbei de izocriteriu corespunzatoare. Aceasta va conduce la o curba corespunzatoare lui J constant, de o valoare mai mica, asa cum este prezentat in figura 7.

Algoritmul de adaptare parametrica corespunzator va avea forma:

. (25)

unde , cu , este amplificarea de adaptare matriciala, I este o mattrice diagonala unitara, si este gradientul crietriului ecuatiei (24) in raport cu .

Din ecuatia (24), se obtine:

. (26)

Dar:

(27)

astfel ca:

. (28)

Introducand ecuatia (28) in ecuatia (26), algoritmul de adaptare parametrica din ecuatia (25) devine:

, (29)

unde F este amplificarea matriciala de adaptare. Doua alegeri sunt posibile:

1. .

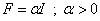2. F > 0(matrice pozitiv definita¹).

Interpretarea geometrica a algoritmului de adaptare parametrica din ecuatia (29) este data    in figura 8.

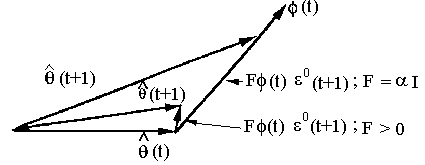
Figura 8:Interpretarea geometrica a algoritmului de adaptare al gradientului.

Algoritmul de adaptare parametrica dat de ecuatia (29) prezinta riscuri de instabilitate daca amplificarea de adaptare (respectiv ) este mare (aceasta se poate intelege cu ajutorul figurii 7). Pentru a evita aceasta problema de instabilitate, se utilizeaza aceeasi abordare a gradientului dar se considera un alt criteriu:

, (30)

Se obtine deci:

. (31)

Din ecuatiile (20) si (22) se obtine:

. (32)

respectiv:

. (33)

Introducand ecuatia (33) in ecuatia (31), algoritmul de adaptare parametrica din ecuatia (25) devine:

. (34)

Acest algoritm depinde de , care este o functie de . Pentru a putea implementa acest algoritm, trebuie exprimat in functie de (adica:

)

Ecuatia (32) se poate rescrie:

. (35)

Primii doi termeni ai membrului drept corespund lui , si, din ecuatia (4), rezulta:

, (36)

ceea ce permite scrierea ecuatiei (25) sub forma:

, (37)

de unde se obtine relatia intre si :

O matrice pozitiv definita este caracterizata prin:

toate elementele de pe diagonala sunt pozitive;

este simetrica ;

determinantii tuturor minorilor principali sunt pozitivi.

. (38)

Algoritmul din ecuatia (34) devine:

. (39)

Acesta este un algoritm satbil oricare ar fi amplificarea F (pozitiva). Impartirea prin introduce o normalizare (ca in paragraful 2.1), care reduce sensibilitatea algoritmului in raport cu F si . De notat ca, daca este cunoscut, acest algoritm este identic celui dat prin ecuatia (9), obtinut prin consideratii euristice.

2.3 Algoritmul celor mai mici patrate recursiv

Utilizand algoritmul gradientului, se minimizeaza la fiecare pas sau, mai exact, deplasarea se efectueaza in directia de descrestere cea mai rapida a criteriului, cu un pas ce depinde de F. Minimizarea lui la fiecare pas nu implica in mod necesar minimizarea sumei:

   

pe un orizont de t pasi, asa cum este prezentat in figura 9. De fapt, in apropierea optimului, daca amplificarea nu este destul de slaba, pot exista oscilatii in jurul minimului. Pe de alta parte, pentru a avea o buna viteza de convergenta de la inceput cand diferenta fata de optim este mare, ar fi de preferat o mare amplificare de adaptare. Algoritmul celor mai mici patrate recursiv ofera de fapt un astfel de profil de variatie a amplificarii de adaptare.

Se considera aceleasi ecuatii pentru proces, modelul de predictie si erorile de predictie utilizate in algoritmul gradientului, si anume ecuatiile(15), ,(22).

Obiectivul este de a gasi un algoritm recursiv avand forma ecuatiei (23) ce minimizeaza criteriul celor mai mici patrate:

(40)

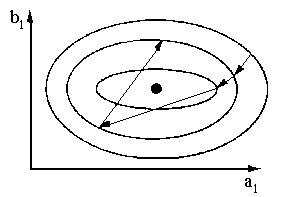
Figura 9: Evolutia unui algoritm de adaptare de tip gradient

Termenul corespunde lui:

. (41)

Astfel predictia iesirii la momentul i (i t) este bazata pe estimatia parametrilor la momentul t obtinuta cu ajutorul a t masurari.

In primul rand se pune problema unui parametru la momentul t ce minimizeaza suma patratelor distantelor dintre proces si modelul de predictie pe un rizont de t masurari.Valoarea lui ce minimizeaza criteriul (40) se obtine cautand valoarea ce anuleaza (42)

De aici, rezulta imediat ecuatia liniara in (dupa aplicarea opertaorului de transpunere):

rezulta:

(43)

2:Este vorba de un minim cu conditia ca a dua derivata a criteriului in raport cu sa fie pozitiva,adica:

Acasta propritate se verifica,in general,in cazul in care t este cel putin egal cu dimensionarea vectorului (vezi,de asemenea,subcapitolul 3)(n.a.),

unde:

(44)

Acest algoritm nu este recursiv.Pentrru a obtine un algoritm recursiv,considera estimatia lui :

(45)

(46)

Se urmareste exprimarea lui ian functie de

(47)

Din ecuatia (45) se obtine:

(48)

Tinand cont de relatia de recurenta (46),ecuatia (48) se poate rescrie:

(49) (50)

Algoritmul de adaptare din ecuatia (50) are o forma recursiva similara algoritmului gradientului dat prin ecuatia (29), cu deosebirea ca matricea de amplificare F(t+1) este acum variabila in timp,pentru ca depinde de masurari(ea corecteaza autmat direct gradientului si lungimea pasului).Se urmareste acum o formula recursiva pentru F(t), plecand de la forma recursiva pentru F^-1(t+1) data prin ecuatia (46). Aceasta se obtine utilizand o lema a inversarii matriceale (data mai jos intr-o forma simplificata), rezultat preluat din Teoria calcului matricial:

Lema: Fie F o matrice de dimensiune(n x n) si un vector de dimensiune n. Atunci: