ROMANIA

MINISTERUL APARARII

ACADEMIA TEHNICA MILITARA

TEZA DE DOCTORAT

CONTRIBUTII LA STUDIUL STABILITATII FLACARILOR DE GAZE COMBUSTIBILE

IN JETURI TURBULENTE

INTRODUCERE

Lucrarea de doctorat analizeaza stabilitatea flacarilor de gaze combustibile in jeturi turbulente, fenomenele specifice schimbului de masa si caldura in jeturi turbulente si aplicatii in procesele arderii difuzive.

Instalatiile de ardere care folosesc combustibil gazos utilizeaza arderea difuziva (flacari difuzive), care este caracterizata prin aceea ca procesul de amestecare intre gazele combustibile si aerul necesar arderii se realizeaza in spatiul de ardere, jeturile de gaze combustibile si aer fiind introduse separat in camera de ardere.

Arderea eficienta a combustibililor gazosi reprezinta o problema de mare importanta, avand in vedere ponderea mare a gazelor naturale in structura generala a consumului de combustibil.

De modul in care este condus procesul de ardere, depinde si realizarea unor produse de calitate in diferitele procese tehnologice.

Obiectivele tezei de doctorat

► Stabilirea de modele fizice pe baza carora sa se determine domeniul de stabilitate a flacarilor difuziv turbulente in jeturi de gaze combustibile.

►Analiza schimbului de masa si de caldura in procesele de ardere difuziva ale combustibililor gazosi.

►Modelarea numerica a fenomenelor specifice arderii difuzive a combustibililor gazosi si analiza stabilitatii flacarilor difuzive in jeturi axial simetrice de gaze combustibile.

►Studiul teoretic si experimental al stabilitatii flacarilor axial simetrice la actiunea laterala a unui jet de aer.

►Utilizarea metodei modelarii fractiei de amestec/PDF (Probability Density Functions) care permite rezolvarea ecuatiilor de transport pentru una sau doua marimi scalare care se conserva in timpul procesului analizat.

►Cercetari numerice asupra difuziei moleculare unidimensionale nestationare in gaze.

►Sistematizarea teoriilor matematice ale stabilitatii miscarilor laminare, la mici perturbatii si miscari in stratul limita.

Capitolul 1 "Cercetari in domeniul arderii difuzive a combustibililor gazosi" prezinta reprezentari matriceale ale functiilor termodinamice, date privind echilibrul chimic si suprafetele de reactie. Pentru procesele care decurg la presiune constanta sunt exprimate marimile variatiilor entalpiei (), entopiei (), caldurii molare izobare , potentialului izobar , precum si valoarea numerica a constantei de echilibru.

Sunt analizati sintetic stabilizatorii de flacara cu scheme de tip Helmholtz, evidentiindu-se potentialul complex al miscarii pentru diedrul nesimetric. Sunt determinate viteza de rupere si lungimea de despridere a flacarii turbulente de difuziune.

Capitolul 2 " Arderea combustibililor gazosi " prezinta bazele teoretice ale arderii combustibililor gazosi ca proces fizico-chimic. In general procesul de ardere este dat de reactia chimica a doua elemente, combustibilul si oxigenul.

Legile de desfasurare a reactiilor chimice in procesele de ardere difera mult de legile clasice ale cineticii chimice. Cauzele acestei abateri se datoreaza faptului ca reactiile chimice in procesele de ardere nu au loc conform ecuatiilor stoichiometrice de oxidare . Mecanismul de reactie in procesul de ardere, conduce la aparitia in flacara a radicalilor, atomilor sau moleculelor cvasistabile cu energie mica de activare.

Este analizata influenta fluctuatiilor turbulentei asupra vitezei de propagare a flacarilor amestecurilor omogene combustibil - aer

Capitolul 3 "Elemente de teoria stabilitatii" prezinta o sinteza a teoriilor stabilitatii miscarii. Cel care a pus bazele problemei clasice a stabilitatii hidrodinamice sub actiunea unor perturbatii mici a fost J.W. Strutt (Lord Rayleigh) in 1880. In 1895, O. Reynolds analizeaza transferul de energie, punand bazele unei a doua metode (cea energetica) in studiul stabilitatii miscarii. Succese remarcabile in studiul stabilitatii miscarilor la mici perturbatii se datoresc lui G.I. Taylor (1923), W. Heisenberg (1924) in analiza curgerii plane Poisenille. Pentru stabilitatea miscarii in stratul limita mentionam cercetarile lui L. Prandtl (1921), O. Tiejens (1925), W. Tallmien (1929).

Autorul sistematizeaza, stabilitatea solutiilor ecuatiilor si sistemelor diferentiale, evidentiind:

forma canonica a problemei de stabilitate;

sistemul autonom;

tipuri de puncte stationare in ;

teoreme de stabilitate si criterii de stabilitate.

Capitolul 4 "Stabilitatea flacarilor de gaze combustibile in jeturi turbulente" contine modelul fizic al conditiei de stabilitate a arderii, elemente privind viteza de propagare a frontului de flacara in jeturi turbulente si determina domeniul de stabilitate al flacarilor in jeturi libere axial simetrice cu viteza ambianta constanta si variabila.

Flacarile difuziv turbulente, in cazul arderii gazelor combustibile in jeturi axial simetrice turbionate au o larga raspandire in practica arderii atat datorita faptului ca au lungimi mai mici, cat si aceea ca au o stabilitate mult mai mare decat in cazul arderii in jeturi turbulente neturbionate, ceea ce conduce la o incinta de ardere mai compacta.

Capitolul 5 "Aplicarea metodelor numerice in studiul arderii difuzive a combusibililor gazosi" contine date privind utilizarea metodei fractiei de amestec / PDF, dezvoltata pentru simularea flacarilor difuziv turbulente si a proceselor de reactie similare in care turbulenta furnizeaza o limitare a vitezei reactiei chimice. Pentru astfel de sisteme, metoda PDF ofera multe beneficii in raport cu formularea vitezei finite.

Modelarea numerica cu metoda volumului finit se aplica unei configuratii care contine trei duze cu axele paralele in acelasi plan (fig. 4.1). Diametrul duzelor este de 5 mm iar distanta dintre axe este de 10 cm. Prin duze curge gaz cu viteza de 20 m/s. Duzele sunt pozitionate in curent de aer cu viteza de 1 m/s.Distributia vitezelor pe sectiunile de intrare a gazului si a aerului se considera constanta. S-au determinat campurile de viteze, de temperaturi si de fractii masice pentru , , si .

Capitolul 6 "Cercetari experimentale, modelari numerice si prelucrari statistice" contine rezultatele experimentale obtinute prin arderea difuziv turbulenta si difuziv-partial cinetica a gazului metan, la patru arzatoare proiectate de autor. Sunt modelate cu Programul FLUENT, flacarile difuziv turbulente axial simetrice in cazul duzelor cu un singur orificiu. Sunt reprezentate variatii ale vitezei globale, temperaturilor, concentratiei , si . Sunt analizate cu Programul FLUENT, stabilitatea flacarilor axial simetrice la actiunea unui jet lateral de aer.

Capitolul 7 "Concluzii si contributii" contine principalele concluzii rezultate din teza de doctorat si contributiile originale ale autorului.

Lucrarea are la baza preocuparile de cercetare teoretica si experimentala ale autorului tezei de doctorat, iar informarea bibliografica cuprinde 121 lucrari din tara si strainatate, din care 10 lucrari sunt ale autorului.

Aduc calde multumiri Conducerii Academiei Tehnice Militare, conducatorului stiintific domnul prof. univ. dr. ing. Sterie Stefan pentru indrumarea permanenta pe toata durata pregatirii prin doctorat, cadrelor didactice care m-au indrumat cu ocazia sustinerii examenelor si referatelor de doctorat, domnului Cdor. prof. univ. dr. ing. Niculae Vlasceanu, membrilor Catedrei de Sisteme Integrate de Aviatie si Mecanica din ATM, cadrelor didactice Prof.univ.dr.ing. Iordache Ion, Prof.univ.dr.ing.Mihaescu Lucian din Universitatea Politehnica Bucuresti, Catedra de Echipament Termoenergetic Clasic si Nuclear, care m-au ajutat la efectuarea cercetarilor experimentale, domnului Cam. prof, univ. dr. ing. Dan - Ioan Ionescu pentru dialogul stiintific purtat in perioada elaborarii tezei de doctorat, domnului Cdor. prof. univ. dr. ing. Constantin Rotaru pentru sugestiile date cu privire la elaborarea tezei de doctorat, colaboratorilor mei, precum si familiei mele pentru sprijinul moral acordat.

CAPITOLUL 1

CERCETARI IN DOMENIUL ARDERII

DIFUZIVE A COMBUSTIBILILOR GAZOSI

Pe plan mondial se face puternic simtita ascensiunea turbinelor cu gaze, ca urmare a dezvoltarii tehnologiei de obtinere a unor materiale rezistente la temperaturi inalte, a unor arzatoare perfectionate cu productie redusa de noxe si a sistemelor de racire eficienta a pieselor aflate in zona temperaturilor inalte. Exista o preocupare majora de informare si corelare a cercetarilor europene in cadrul unor programe internationale de tip FP V si FP VI la care a aderat si Romania, prin care se doreste implementarea acestor sisteme moderne de producere a energiei electrice si termice cu un grad ridicat de eficienta si in conditii de maxima protectie a mediului [4, 20, 35, 65, 70, 114].

1.1.1 Ecuatiile fundamentale pentru substantele simple

Pentru substantele individuale aflate intr-o anumita faza, caldurile molare izobare se aproximeaza in functie de temperatura prin expresii polinomiale de forma [4, 20, 35, 65, 70, 114]:

, (1.1)

sau prin combinatii liniare ale unor functii cu :

, (1.2)

Utilizand derivatele entalpiei H si ale entropiei S in raport cu temperatura la presiune constanta:

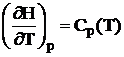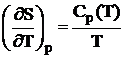; , (1.3)

Notand temperatura cu T si inlocuind relatiile (1.12) si (1.13) in (1.6) si (1.7) obtinem:

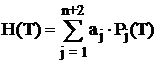, (1.18)

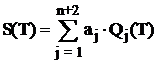. (1.19)

1.1.2 Echilibrul chimic

Echilibrul chimic pentru amestecuri de gaze care reactioneaza se defineste in termodinamica chimica pe baza principiului al doilea al termodinamicii, cu ajutorul potentialelor chimice.

Principiul al doilea al termodinamicii se poate exprima sub forma

TdS dH - Vdp,

de unde rezulta, pentru un sistem in care au loc procese la presiune si temperatura constanta:

dG_p,T (1.25)

unde: G = H - TS este entalpia libera, sau energia libera Gibbs. Prin urmare, pot avea loc numai procesele insotite de scaderea energiei libere Gibbs; cand energia libera Gibbs atinge valoarea minima, care se mentine in continuare constanta, sistemul se afla la echilibru chimic.

Pentru un amestec de j substante, fiecare in cantitatile v_i moli, diferentiala totala dG este in general

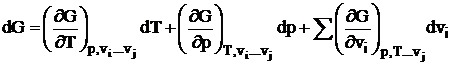, (1.26)

unde:

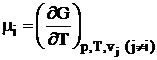- potentiale chimice ale componentilor i.

1.1.3 Suprafata de reactie

Ecuatia suprafetei de reactie in flacara difuiziva pentru procesul adiabatic se poate obtine prin rezolvarea ecuatiei [4, 20, 35, 65, 70, 114]:

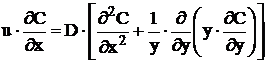(1.39)

in care 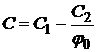,-sunt concentratii, iar reprezinta cantitatea de moli de oxigen care reactioneaza cu un mol de gaze combustibile,cu urmatoarele conditii la limita:

pentru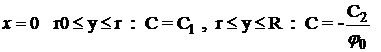

si (1.40)

Integrarea ecuatiei (1.39) permite determinarea interdependentei dintre concentratiile si in tot spatiul flacarii. Din conservarea entalpiei totale in orice punct al spatiului flacarii se obtine relatia:

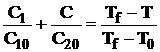, (1.41)

In cazul camerei de ardere cilindrice, miscare axial simetrica, din (1.45) cu conditiile (1.40), se obtine solutia:

, (1.46)

in care reprezinta radacinile ecuatiei , iar si sunt functiile Bessel de ordinul zero si unu.

1.3.1 Calculul parametrilor de stare in vecinatatea punctului Chapman- Jouguet superior (CJs)

In fig. 1.3 se reprezinta variatia presiunii si entropiei, in vecinatatea punctului Chapman-Jouguet superior:

Fig. 1.3 Variatia presiunii in vecinatatea punctului Chapman-Jouguet superior

Fig. 1.4 Variatia entropiei in vecinatatea punctului Chapman-Jouguet superior

1.4 Difuzia moleculara unidimensionala nestationara in gaze

Difuzia pura sau moleculara se caracterizeaza prin diminuarea gradientilor de concentratie existenti in limitele unei faze oarecare si se produce prin migrarea atomilor sau moleculelor in lipsa curentilor de convectie.

Difuzia in regim stationar are loc in cazul in care intre doua puncte se mentine o diferenta constanta de concentratie, fenomenul fiind descris de prima lege a lui Fick [4, 20, 35, 65, 70, 114]:

[kmoli/m²s] , (1.51)

unde J este fluxul de difuzie (J = const.), D [m²/s] - coeficientul de difuzie, C - concentratia substantei care difuzeaza (molecule/m), - gradientul de concentratie.

Difuzia in regim nestationar se caracterizeaza prin variatia in timp a fluxului de difuzie si este descrisa de legea a doua a lui Fick

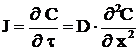. (1.52)

Pe baza teoriei cinetice a gazelor se deduce relatia :

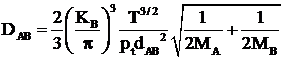[m/s²] , (1.53)

unde D_AB este coeficientul de difuzie a gazelor A si B care difuzeaza , K_B este constanta lui Boltzmann (K_B = 1,38 10 ^{- 9}) [J/molec*K], d_AB - diametrul mediu al moleculelor (d_AB = (d_A + d_B) / 2 [m]) , M_A,M_B - mase moleculare [Kg/mol] , p_t - presiunea totala [N/m²], T - temperatura [K] .

1.5 Stabilizatori de flacara

1.5.1 Scheme de tip Helmholtz

Metoda hodografica a lui S.A.Ciaplighin este aplicabila la problemele de tip Helmholtz si Kirchoff, probleme care pun in evidenta o marime specifica miscarilor care se studiaza si anume viteza caracteristica. Aceasta marime se considera a fi viteza de pe liniile libere, care are o valoare constanta, conform teoriei miscarilor cu linii de discontinuitate, pentru viteze. Teoria de mai sus a fost imaginata, pentru a se indeparta paradoxul lui D'Alembert, care consta in afirmarea lipsei de rezistenta la inaintare a unui corp care se misca intr-un fluid.

Teoria lui Helmholtz, reluata si de Kirchhoff, conduce la valori prea mici pentru rezistenta ce o incearca un solid in miscarea sa prin mediul fluid; acest lucru nu este surprinzator deoarece teoria aceasta neglijeaza complet efectele turbionare care se produc in spatele obstacolului, pe care singura vascozitatea le poate explica si admite doar existenta unei zone in care fluidul este antrenat cu obstacolul.

Teoria lui Helmholtz a fost dezvoltata prin metoda lui Levi-Civita care exprima solutia nedefinita a problemei ca o functionala de una sau mai multe functii q(s), intim legate de forma obstacolului si a peretilor solizi, dar a carei determinare cere rezolvarea unor ecuatii functionale neliniare. A doua problema pe care o pune teoria lui Helmholtz, anume, determinarea miscarii care corespunde unor pereti dati si nu construiti, dupa ce s-au dat functiile q(s), peretii fiind definiti prin ecuatia lor intrinseca, cere rezolvarea ecuatiilor functionale amintite. Astfel ipoteza lui Helmholtz revine la a neglija fenomenele turbionare foarte complicate care se intampla in aceasta regiune si a considera acolo fluidul in repaus, deci legat de obstacol (fig. 1.10)

Fig. 1.10 Modelul lui Helmholtz

Se formeaza astfel in spatele obstacolului o regiune cu fluid imobil, pe care experienta o confirma pentru numerele lui Reynoltz foarte mari, iar traiectoriile particulelor fluide () detasate de pe frontiera obstacolului nu se vor mai intalni in spatele acestuia, ci se vor intinde la infinit aval, cu directii asimptotice paralele cu directia vitezei a fluidului, la infinit amonte (directia generala de miscare a curentului).

1.5.4 Modelul Cheng - Kovity

Modelul Cheng si Kovitz, pentru stabilizarea flacarii la spatele obstacolului, este aratat in fig. 1.18.

Vartejul de gaze calde, recirculate la spatele obstacolului, se compune din doi curenti: unul de acelasi sens cu curentul principal in contact cu acest curent, celalalt curgand in sens contrar in apropierea axei sistemului, cu cei doi curenti mentionati [4, 20, 35, 65, 70, 114].

Pentru efectuarea calculelor se presupune ca flacara laminara este ancorata in punctul P la distanta x_i de marginea A a obstacolului. Pentru ca in punctul P sa poata sa ia nastere si sa se mentina un front de flacara, este necesar ca aportul de caldura preluata de la frontul de flacara de gazele vartejului pe distanta PS, la care se adauga caldura degajata prin reactiile de ardere din interiorul vartejului, sa fie suficienta sa compenseze pierderile de caldura spre exterior si caldura transmisa pentru aprinderea amestecului combustibil proaspat pe distanta AP.

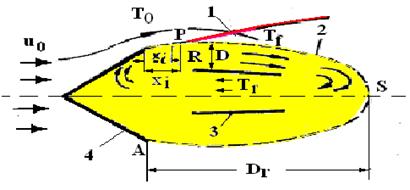
Fig. 1.18 Modelul Cheng si Kovitz pentru calculul distantei

de acrosare a flacarii x_i , la spatele obstacolului:

1 - frontul de flacara; 2 - linie de separatie intre zona de curgere

si de recirculatie; 3 - linie de stagnare; 4 - obstacol V.

Din ecuatia de bilant de caldura bazata pe ipotezele de mai sus rezulta, relatia:

(1.89)

in care: exponentul n = 3/2 4/3; este distanta medie de la marginea obstacolului A (fig.1.18) pana la centrul de aprindere P; D_r - lungimea arcului AS; - constanta adimensionala; c_p - caldura specifica la presiune constanta a amestecului combustibil proaspat; T_f, T_r, T₀ - temperatura zonei flacarii, zonei de recirculatie si amestecului combustibil proaspat: - caldura de ardere, in J g^-1; E - energia de activare, in J ∙ mol^-1; R - constanta universala a gazelor; A - factorul de frecventa in expresia vitezei de reactie; - viteza curentului in amonte de obstacol, in cm ∙ s^-1; D - distanta intre linia de separatie 2 si linia de stagnare 3 (fig. 1.18), in cm; l - lungimea efectiva (cm) a placii plate a obstacolului care defineste conditiile de frecare inainte de zona de stagnare din spatele obstacolului).

1.6 Determinarea vitezei de rupere a flacarii turbulente de difuziune

Daca se noteaza cu viteza curentului pe axa jetului, conditia de stabilitate a flacarii este:

. (1.91)

Daca se considera pentru expresia data de Williams si Bollinger,

, (1.92)

valabila pentru Re = 3 00080000), in care: este viteza maxima a scarii laminare, in cm s^-1; d ₀ - diametrul gurii arzatorului, in cm, iar pentru u_m expresia data de Abramovici.

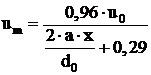, (1.93)

in care: este viteza curentului in gura arzatorului; x - distanta de la gura arzatorului pana la sectiunea de calcul a jetului (fig.8.38), si daca se inlocuiesc in ecuatia (8.28) rezulta: (1.94)

unde: , este lungimea raportata a flacarii pana la sectiunea la care se realizeaza egalitatea C_m = C_s , adica concentratia de combustibil gazos pe axa jetului este egala cu concentratia stoichiometrica a amestecului combustibil, ( depinde numai de natura combustibilului gazos); - diametrul raportat al zonei de amestecare a jetului in sectiunea transversala in care concentratia pe axa jetului C_m = C_s ( depinde numai de natura combustibilului gazos); n_s - vascozitatea cinematica a amestecului combustibil - aer la ruperea flacarii, in ; a - coeficientul de structura al jetului (a 0,07) ; d₀ - diametrul, in mm; , in m s^-1.

1.7 Determinarea lungimii de desprindere a flacarii turbulente de difuziune

Pentru a calcula variatia concentratiei C in lungul jetului, poate fi adoptata o relatie de forma:

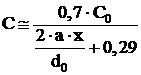, (1.102)

in care C₀ este concentratia de combustibil gazos in gura arzatorului.

Pentru M_a = M_g, rezulta:

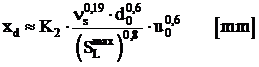, (1.104)

iar pentru cazul , rezulta:

, (1.105)

unde d₀ este dat in mm.

CAPITOLUL 2

ARDEREA COMBUSTIBILILOR GAZOSI

2.1 Introducere

Arderea eficienta a combustibililor gazosi reprezinta o problema de mare importanta, avand in vedere ponderea mare a gazelor naturale in structura generala a consumului de combustibil [9, 30, 33, 35, 40, 63, 91, 115].

In functie de marimea componentilor timpului de ardere, arderea se considera cinetica, difuziva sau intermediara.

In general, timpul total de ardere se compune din doua parti: timpul necesar realizarii contactului fizic intre combustibil si aerul necesar arderii si timpul necesar desfasurarii reactiei chimice .

Cand componentele care reactioneaza sunt in stare gazoasa, este timpul de amestecare.

Cand timpul de amestecare , este cu mult mai mic decat timpul , procesul de ardere este determinat de viteza de reactie chimica, arderea in acest caz este denumita ardere cinetica.

Conform terminologiei utilizate in literatura de specialitate, in cazul in care timpul este cu mult mai mare decat cel de reactie chimica , arderea este considerata difuziva; iar in cazul in care cei doi timpi sunt comparabili, arderea este denumita intermediara.

2.2 Bazele teoretice ale arderii combustibililor gazosi

In general procesul de ardere este dat de reactia chimica a doua elemente, combustibilul si oxigenul [9, 30, 33, 35, 63, 115].

Reactia chimica intre substantele A si B, care decurge cu formarea produselor M si N, poate fi descrisa de ecuatia stoichiometrica, care se prezinta sub forma:

, (2.1)

in care:

A; B; M; N reprezinta formulele chimice ale substantelor respective;

a, b, m, n sunt coeficientii stoichiometrici;

Q - efectul termic al reactiei.

Pentru cele mai raspandite gaze combustibile utilizate in tehnica arderii, rezulta urmatoarele ecuatii stoichiometrice:

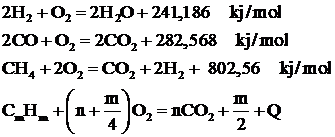
Conform legii actiunii maselor, viteza reactiilor chimice depinde de concentratia substantelor care reactioneaza si de temperatura.

Intr-o forma generala aceasta viteza poate fi scrisa sub forma:

, (2.2)

in care: w este viteza reactiei chimice, care se considera ca este egala cu viteza de scadere a concentratiilor substantelor respective; C - concentratia substantelor care reactioneaza; T - temperatura initiala.

Dependenta constantei reactiei chimice de temperatura, este data de legea lui Arhenius, care are forma:

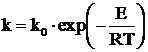, (2.4)

in care:

k₀ - constanta;

E - energia de activare, kj/mol;

R - constanta universala a gazelor, ;

T - temperatura absoluta, ⁰K.

Constanta k₀, se poate lua proportionala cu , desi unii cercetatori considera ca este independenta de temperatura.

2.2.1.2 Mecanismul de reactie in lant in procesele de ardere

Legile de desfasurare a reactiilor chimice in procesele de ardere difera mult de legile clasice ale cineticii chimice. Cauzele acestei abateri se datoreaza faptului ca reactiile chimice in procesele de ardere, nu au loc conform ecuatiilor stoichiometrice de oxidare . Mecanismul de reactie in procesul de ardere, conduce la aparitia in flacara a radicalilor, atomilor sau moleculelor cvasistabile cu energie mica de activare [9, 33, 35, 40, 63, 115].

Este de remarcat ca in afara produsului final de reactie, ramane in amestec si o cantitate de produse intermediare active, care continua lantul de transformari.

Cea mai studiata reactie in lant este cea dintre hidrogen si oxigen.

Conform ecuatiei stoichiometrice rezulta:

ceea ce arata ca reactia este de gradul trei.

Conform literaturii de specialitate, un atom de hidrogen format in amestec poate reactiona cu o molecula stabila de oxigen, conform schemei:

H H

O+H₂ OH+H₂ H₂O

H+O₂ H₂O (2.9)

OH+H₂

sau:    H

Astfel rezulta ca, la fiecare atom de hidrogen se formeaza, intr-un ciclu doua molecule de apa si trei noi atomi de hidrogen, care la randul lor, pot dezvolta trei cicluri asemanatoare, daca nu are loc reactia de anihilare a centrilor activi, conform relatiei:

. (2.10)

Reactia in lant poate fi de tip ramificat, cand intr-un ciclu se formeaza mai multi centri activi sau de tip neramificat, cand numarul de centri activi formati pe ciclu este egal cu cel initial in ciclu.

Viteza de formare a centrilor activi in reactia in lant este data de relatia:

, (2.11)

in care:

w_a este viteza de formare a centrilor activi intr-un ciclu;

c_a - concentratia centrilor activi;

f - constanta de ramificare a lantului;

g - constanta de rupere a lantului;

- viteza de ramificare a ciclurilor;

- viteza de rupere a lantului.

Legea de variatie in timp a concentratiei centrilor activi, care are forma:

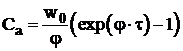. (2.12)

2.3.1 Schimbul de masa si de caldura in flacarile difuzive laminare

2.3.1.1 Ecuatiile proceselor de schimb de masa si de caldura

In prezent datorita lucrarilor fizicienilor S.R. de Groot, J. Prigogine, L. Onsager, A.H. Lakov s-a creat posibilitatea de aplicare a teoriei fenomenologice in studiul proceselor de schimb de masa si caldura in domeniul curgerii laminare, teorie care se bazeaza pe rezultatele obtinute de cercetarile efectuate in domeniul termodinamicii proceselor ireversibile [9, 30, 33, 35, 40, 63, 91, 115].

Conform termodinamicii proceselor ireversibile fluxul specific de masa este dat de relatia:

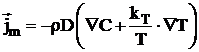, (2.16)

in care:

D este coeficientul de difuzie moleculara;

r - densitatea sistemului;

C - concentratia;

k_T - constanta de termodifuzie;

T - temperatura

Fluxul specific de caldura conform , este dat de relatia:

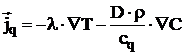, (2.17)

in care:

este coeficientul de conductibilitate termica.

Conform teoriei cinetico-moleculare a gazelor ideale coeficientul de difuzie moleculara este dat de relatia:

, (2.19)

- conductivitatea termica

Daca se utilizeaza coeficientul de difuzivitate a temperaturii fluidului a:

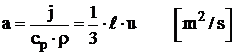, (2.20)

- coeficientul de vascozitate dinamica,

,

din care rezulta vascozitatea cinematica ,

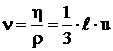, , (2.21)

In concluzie, pentru gazele ideale, invariantii Prandtl, , Schmidt, si Lewis, , sunt egali cu unitatea, in timp ce pentru gazele reale difera de unitate. Este de remarcat ca, acesti invarianti au un rol deosebit in procesele de transfer de masa si de caldura.

In cazul proceselor de ardere laminara, ecuatia de transport de masa are forma:

in care termenul w(C,T) reprezinta viteza de reactie chimica care depinde atat de temperatura cat si de concentratii, iar este derivata substantiala a concentratiei.

Ecuatia transferului de caldura in cazul arderii difuziv laminare, conform , in care se vor neglija termenii disipativi si se va considera sistemul izolat adiabatic, se poate scrie sub forma:

, (2.24)

Se mai adauga ecuatia continuitatii, care are expresia:

, (2.25)

si ecuatia Navier-Stokes, in care se neglijeaza termenii disipativi si care conform are forma:

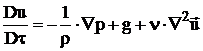, (2.26)

2.3.1.2 Schimbul de masa si caldura in flacarile difuziv turbulente ale gazelor combustibile

Schimbul de masa si de caldura in jeturile turbulente este intensificat puternic, fata de curgerea laminara deoarece in afara schimbului molecular, apare si un schimb de turbioane, care trec dintr-un strat in altul [9, 33, 35, 63, 91, 115].

Conform teoriei lui Prandtl, valoarea medie patratica a pulsatiei vitezei 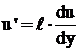, rezulta conform relatiei (2.29), ca

. (2.30)

Avand in vedere ca, scara turbulentei dupa teoria lui Taylor, este , rezulta dupa teoria acestuia ca:

. (2.31)

Astfel, prin analogie, se poate vorbi de coeficient turbulent de conductie si de vascozitate cinematica turbulenta n_t

2.3.1.3 Schimbul de masa si caldura intre jeturile de gaze

combustibile si aer

Este de mentionat faptul ca, procesul de amestecare dintre jetul de combustibil si aerul necesar arderii are o influenta majora asupra caracteristicilor flacarii (lungime, stabilitate si radiatie) [9, 30, 35, 40, 63, 115].

Un jet este caracterizat de trei zone, care se pot distinge, conform figurii 2.2:

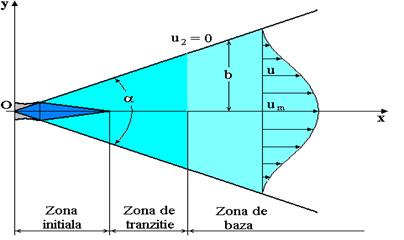
Fig. 2.2 Zonele jetului turbulent liber cu viteza ambianta nula

Cele trei zone ale jetului sunt:

- zona initiala, , in care se stabileste un nucleu potential, in care se conserva toate marimile initiale ale jetului;

- zona de tranzitie , in care are loc o redistribuire ale marimilor initiale in sectiunile transversale:

- zona de baza in care distributia vitezelor, concentratiilor si temperaturilor in sectiunile transversale ale jetului sunt de tipul functiilor Gauss.

In ceea ce priveste zona de tranzitie, aceasta este foarte mica, fapt pentru care in unele cercetari este neglijata.

Functiile de distributie in sectiunile transversale din zona de baza a jeturilor turbulente axial simetrice libere sunt conform literaturii de specialitate:

(2.33)

unde:

u - este viteza intr-un punct oarecare dintr-o sectiune oarecare din zona de baza a jetului:

v_m - viteza pe axa jetului, in aceeasi sectiune;

c - concentratia in punctul de coordonate (x,y) al unei sectiuni transversale din zona de baza a jetului;

c_m - concentratia pe axa jetului, in aceeasi sectiune;

- temperatura pe granita jetului;

T_m - temperatura pe axa jetului;

T - temperatura dintr-un punct oarecare din aceeasi sectiune a jetului;

- ordinata adimensionala;

a - coeficientul de structura a jetului, coeficient ce depinde de unghiul de evazare a jetului a

. (2.34)

2.4.1 Viteza de propagare a frontului de flacara a combustibililor gazosi in cazul curgerii laminare

Aceasta viteza este cunoscuta in literatura de specialitate sub numele de viteza normala de propagare a frontului de flacara sau viteza normala de ardere .

Pe baza teoriei termice, Kolmogorov, Petrovski si Piscunov arata ca viteza normala de ardere a flacarilor de gaze combustibile se poate determina cu relatia:

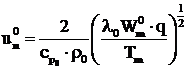, (2.48)

Pentru determinarea valorii maxime a vitezei normale de ardere a unui amestec de mai multe gaze combustibile cu aerul de ardere, se poate utiliza relatia:

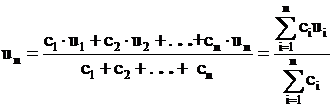, (2.49)

In practica, viteza normala de propagare a frontului de flacara se determina cu arzatorul Bunsen, folosind flacara laminara, la care frontul de flacara este dat de aria laterala a conului de flacara, conform figurii alaturate:

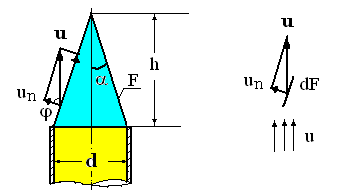
Fig. 2.4 Conul frontului flacarii laminare la iesirea

amestecului gazelor combustibile din tub

Conform teoriei lui Gouy-Michelson, viteza normala de propagare a frontului de flacara va fi data de relatia care asigura echilibrul suprafetei elementare dF, conform figurii 2.4:

. (2.52)

Se poate scrie

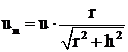, (2.56)

Pe baza relatiei (2.56), se poate determina viteza normala de propagare a frontului de flacara, folosind metoda becului Bunssen.

In figura 2.6 se prezinta variatia vitezei normale de propagare a frontului de flacara in amestecul de gaz metan si aer in functie de temperatura si concentratie.

Fig. 2.6 Variatia vitezei normale de propagare a frontului de flacara a

amestecului de CH₄ cu aer in functie de concentratie si teemperatura

Din analiza graficelor din figura 2.6 se constata ca la o crestere a temperaturii amestecului de la 20 C la 680 , viteza normala maxima de propagare a frontului de flacara a gazului metan creste de peste zece ori, adica de la 29 cm/s la 315 cm/s,

Viteza de propagare a frontului de flacara la curgerea turbulenta in cazul arderii combustibililor gazosi

Pentru cazul curgerii cu scara mare a turbulentei ( fiind grosimea frontului de flacara), pentru determinarea vitezei turbulente de propagare a frontului de flacara se poate utiliza relatia:

, (2.60)

in care:

D_t - este coeficientul turbulent de difuzie, iar n coeficientul de vascozitate cinematica a amestecului;

- scara turbulentei.

O formula similara cu (2.60), pentru cazul curgerii cu scara mica a turbulentei este luat in calcul si schimbul molecular de masa:

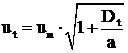, (2.62)

2.5 Limitele de aprindere in amestecurile diverselor gaze cu aer si cu oxigen la presiunea atmosferica si temperatura de 293 K

Propagarea flacarii este posibila intre limite determinate de concentratie a combustibilului in amestec (tabelul 2.1) [35, 63, 115].

Tabelul 2.1

2.6 Influenta temperaturii initiale

Viteza de propagare a frontului de flacara depinde de temperatura initiala a amestecului si temperatura gazelor T, conform relatiei:

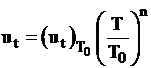, (2.66)

Variatia lungimii flacarii se calculeaza cu elatia:

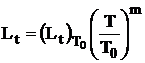, (2.67)

Variatia temperaturii gazelor de ardere se exprima astfel:

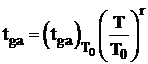, (2.69)

2.7 Influenta presiunii

Viteza de reactie depinde de presiune, conform legii exponentiale in care n este gradul reactiei. Daca se tine seama de relatia (exprima viteza de reactie in functie de presiune, la temperatura constanta, pentru substante care reactioneaza in concentratii volumetrice relative), rezulta [35, 63, 115]:

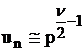(2.69)

Viteza normala masica de ardere este:

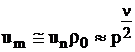. (2.70)

In cazul combustibilului format dintr-un amestec de gaze, viteza normala de propagare a frontului de flacara se determina cu relatia:

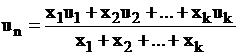. (2.73)

in care x₁, x_k , reprezinta participatiile componentelor, iar u₁ u_k vitezele normale de propagare a frontului de flacara pentru componente.

2.8 Influenta fluctuatiilor turbulentei asupra vitezei de propagare a flacarilor amestecurilor omogene combustibil - aer

Viteza de propagare a flacarilor turbulente se determina ca functie de parametrii initiali: compozitia amestecului, presiunea si temperatura initiala, turbulenta initiala a curentului in miscre.

Pentru : ,

: ,

rezulta urmatoarele valori numerice si reprezentari grafice:

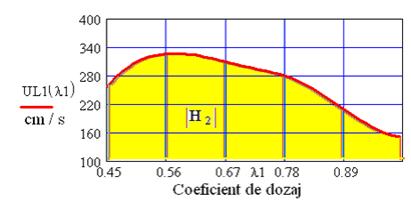
Fig. 2.7 Variatia vitezei de ardere laminara a hidrogenului in functie de

coeficientul de dozaj

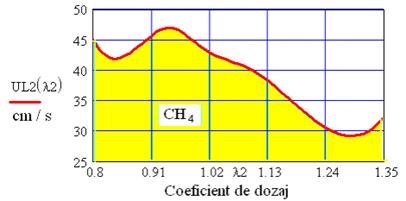
Fig. 2.8 Variatia vitezei de ardere laminara a gazului metan in functie de

coeficientul de dozaj

Determinarea ecuatiei de regresie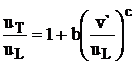

Se aplica metoda celor mai mici patrate pentru determinarea coeficientilor b si c. Se aplica urmatorul algoritm:

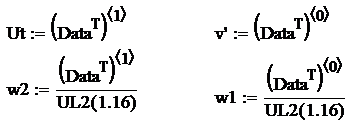
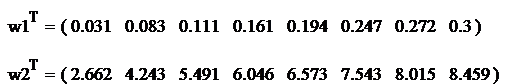
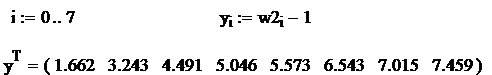
Se logaritmeaza relatia si se fac notatiile:

,

Rezulta: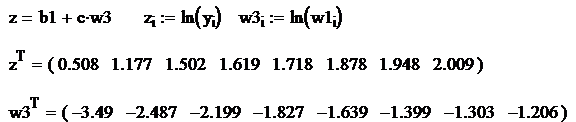

Ecuatia de regresie 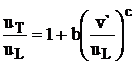ia forma: 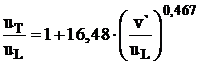, care permite determinarea vitezei turbulente la arderea gazului metan in functie de viteza laminara de ardere si de fluctuatia turbulentei.

Reprezentarea grafica a ecuatiei de regresie se efectuiaza pentru valorile relative ale fluctuatiilor:

Fig. 2.9 Variatia vitezei turbulente a gazului metan in functie de fluctuatia

Relativa a turbulentei

CAPITOLUL 3

ELEMENTE DE TEORIA STABILITATII

Problema stabilitatii miscarilor fluidelor s-a pus practic in paralel cu aceea a mecanicii fluidelor. Experientele lui G. Hagen (1839) si J. Poisenille (1841), ca si cele ale lui O. Reynolds (1883) reprezinta punctul de plecare al studiilor legate de stabilitatea miscarii. Printre precursori mai mentionam pe H. Helmholtz (1848) care analizeaza suprafetele de discontinuitate ale vitezei in miscari stratificate si Tyndal (1867) care studiaza instabilitatea de tip Helmholtz la frontiera unui jet de aer circular.

Cel care a pus bazele problemei clasice a stabilitatii hidrodinamice sub actiunea unor perturbatii mici a fost J.W. Strutt (Lord Rayleigh) in 1880. In 1895, O. Reynolds analizeaza transferul de energie, punand bazele unei a doua metode (cea energetica) in studiul stabilitatii miscarii. In anii 1907 - 1908, McF. Orr si A. Sommerfeld au dedus pentru miscari paralele, ecuatia care le poarta numele, pentru perturbatii de forma:

(3.1)

denumite unde transversale Tollmien - Schlichting, dupa numele celor care au utilizat primii asemenea forme de perturbatii in studiul stabilitatii. Succese remarcabile in studiul stabilitatii miscarilor la mici perturbatii se datoresc lui G.I. Taylor (1923), W. Heisenberg (1924) in analiza curgerii plane Poisenille. Pentru stabilitatea miscarii in stratul limita mentionam cercetarile lui L. Prandtl (1921), O. Tiejens (1925), W. Tallmien (1929).

In lucrarile elaborate de Chandrashekhar, S.(1961), Drazin, P.G. (1981), Josep, D.D. (1976), Li, W.H, Lam, S.H. (1964), Shaw, M. (1964), Staniukovici, K.P. (1960) sunt dezvoltate studii privind teoria clasica a stabilitatii hidrodinamice.

3.2 Teoreme de stabilitate. Criterii de stabilitate

Pentru sistemele liniare, studiul stabilitatii miscarii se refera la studiul semnului radacinilor ecuatiei caracteristice atasata ecuatiilor diferentiale ale miscarii perturbate [31, 49]:

(3.46)

In ipoteza , conditia necesara, dar nu si suficienta, ca ecuatia algebrica (3.46) sa aiba radacini reale negative sau radacini complex conjugate cu parti reale negative ( conditii de stabilitate a miscarii), este ca toti coeficientii sa fie pozitivi.

3.2.1 Criteriul de stabilitate Routh - Hurwitz

Presupunand conditia , (k = 0, 1,., n) in (3.3.1) criteriul Routh-Hurwitz are urmatorul enunt: conditia necesara si suficienta ca ecuatia caracteristica (3.3.1) sa aiba radacini reale negative sau complex conjugate cu partile reale negative, este ca toti determinantii Hurwitz D_k, , formati cu coeficientii ecuatiei caracteristice sa fie pozitivi, adica [31, 49

; ,

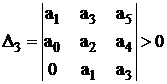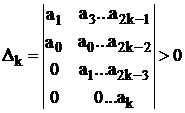, . . ., (3.47)

Pentru ecuatii caracteristice de gradul trei avem conditiile

, , (3.48)

iar pentru cele de gradul patru:

; ,

;     (3.49)

In cazul sistemelor cu , calculele devin laborioase, fapt pentru care se recomanda metode geometrice legate de criteriul de stabilitate Mihailov.

3.2.2 Criteriul de stabilitate Mihailov

Presupunem ca ecuatiei caracteristice (3.46) ii corespunde conditia

, .

Enuntul criteriului: pentru ca toate radacinile ecuatiei caracteristice (3.46) sa aiba parte reala negativa, este necesar si suficient ca la variatia continua a lui y de la zero la , vectorul , reprezentat cu originea in originea axelor (), sa se roteasca in sens trigonometric cu unghiul .

3.2.3 Metoda Liapunov. Functia lui Liapunov

Se considera cazul sistemelor cu doua grade de libertate. Studiul stabilitatii miscarii se face cu ajutorul unei functii reale 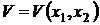- denumita functia lui Liapunov, definita intr-o vecinatate a pozitiei de echilibru (,), cu

, , mic si pozitiv, care are urmatoarele proprietati:

1) Derivata totala a lui in punctul de echilibru ( ,) este nula,

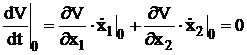. (3.51)

2) Daca este pozitiv definita atunci graficul lui este o curba inchisa ce contine originea coordonatelor.

Daca , atunci graficul lui este dispus in interiorul curbei si graficele nu au puncte comune.

3.2.4 Teorema lui Liapunov

Daca ecuatiilor diferentiale ale miscarii perturbate se ataseaza o functie , definita ca semn ( plus sau minus), cu proprietatea definita ca semn, dar de semn opus lui sau , atunci miscarea neperturbata este stabila.

Daca in enuntul teoremei lui Liapunov se renunta la conditia ,atunci miscarea neperturbata este asimptotic stabila.

3.2.7 Ecuatiile primei aproximari pentru sisteme autonome

Sistemului dinamic autonom

,

, (3.56)

i se asociaza sistemul liniar

(3.57)

denumit sistemul ecuatiilor primei aproximari, care, in multe situatii, da indicatii exacte asupra stabilitatii miscarii neperturbate. In acest sens se utilizeaza doua teoreme ale lui Liapunov:

(I) Daca partile reale ale tuturor radacinilor ecuatiei caracteristice atasata sistemului primei aproximari (3.57) sunt negative, atunci solutia nula a sistemului autonom (3.56) (miscarea neperturbata) este asomptotic stabila, indiferent de forma termenilor neliniari , ;

(II) Daca cel putin una din partile reale ale unei radacini a ecuatiei caracteristice atasata sistemului primei aproximari (3.57), este pozitiva, atunci solutia nula a sistemului autonom (3.56) (miscarea neperturbata) este nestabila, indiferent de forma termenilor neliniari, .

3.2.8 Stabilitate absoluta. Criteriul lui V.M. Popov

Se presupune ca ecuatiile diferentiale ale miscarii perturbate au forma:

,

, (3.58)

unde ,,,,, si sunt constante.

Fie functie neliniara pentru care solutia nula a sistemului (3.58) este stabila (miscarea neperturbata este stabila). In virtutea continuitatii, aceasta solutie va fi stabila pentru o multime de functii ale caror grafice sunt dispuse in vecinatatea graficului functiei (fig. 3.1). Graficele tuturor acestor functii in planul se afla intre doua drepte:

,, cu .

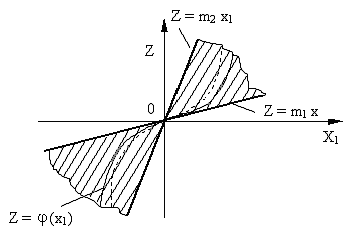
Fig. 3.1 Graficul in domeniul de stabilitate

3.3 Stabilitatea unei miscari laminare cunoscute

Sa consideram ca avem o anumita miscare laminara si ca dorim sa stim daca aceasta miscare este stabila sau nu. Miscarea considerata, denumita miscare de baza, va fi caracterizata printr-un camp de viteze si presiuni va satisface sistemul de ecuatii (3.68) si (3.69) cu conditii initiale si la limita corespunzatoare, respectiv:

, (3.71)

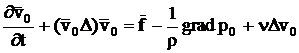(3.72)

, (3.73) , (3.74)

unde relatiile (3.73), (3.74 reprezinta formal conditiile initiale si respectiv la limita, (e) reprezentand o suprafata solida la care fluidul adera, adica fluidul sa aiba viteza suprafetei pe aceasta.

Presupunem o miscare perturbata caracterizata prin viteze si presiuni diferite:

_.. (3.75)

Miscarea de baza poate fi perturbata prin mecanisme diferite, dintre care mentionam:

- frontierele solide se pot deplasa sau modifica (oscilatii sau deformatii);

- injectie de fluid;

- conditii la infinit variabile sau variatia conditiilor la limita.

Din punctul de vedere al stabilitatii in sensul lui Liapunov intereseaza in primul rand posibilitatea de modificare a miscarii datorita modificarii conditiilor initiale (3.3.6). Se va studia miscarea (3.3.8) care rezulta din modificarea conditiilor initiale prin impunerea unor perturbatii initiale. In aceste conditii miscarea este caracterizata de urmatoarele ecuatii si conditii:

(3.76)

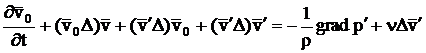
(3.78)

. (3.79)

Problema determinarii miscarii perturbate revine la a gasi din sistemul (3.76) (3.79), unde si sunt cunoscute.

Formularea matematica a conditiilor de stabilitate, in sensul lui Liapunov, este urmatoarea:

"miscarea este stabila daca pentru un numar pozitiv e>0 exista un alt numar pozitiv d > 0, eventual depinzand de e, astfel incat:

(3.80)

cand:

(3.81)

sau altfel notat:

(3.81

unde cu s-a notat norma unui camp scalar sau vectorial, definita prin:

(3.82)

in tot domeniul miscarii D.

Conditia de stabilitate asimptotica, in sensul lui Liapunov va fi:

cand (3.83)

Daca nu se indeplinesc conditiile (3.81) (3.83) atunci miscarea va fi instabila.

3.3.2 Miscari paralele de baza si perturbate

Miscarile paralele reprezinta o clasa de miscari fara forte de inertie. Asemenea miscari se pot realiza intr-un strat de fluid de grosime constanta marginit de suprafete solide plane si paralele, miscari realizate fie prin deplasarea suprafetelor cu o viteza relativa una fata de alta (miscari de tip Couette), fie datorita unui gradient de presiune (miscari de tip Poisenille), fie prin combinarea celor doua miscari precedente [7, 16, 31, 49, 89, 109].

Fie x, z coordonatele carteziene care definesc un plan paralel cu suprafetele solide si fie y coordonata normala pe aceasta. Miscarea de baza paralela stationara este caracterizata prin componentele vitezei in directiile x si z:

(3.94)

In aceste conditii, ecuatiile Navier-Stokes (3.3.5) se scrie sub forma:

(3.95)

Ecuatia de continuitate si forma vectoriala a ecuatiilor

Navier-Stokes in marimi adimensionale

Ecuatia de continuitate si forma vectoriala a ecuatiilor Navier-Stokes se pot scrie in marimi adimensionale:

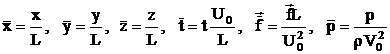
unde L este o valoare caracteristica pentru lungimi, iar U0 pentru viteze. Se mai noteaza:

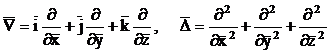(3.102)

iar sistemul (3.99), (3.100) se scrie sub forma adimensionala:

(3.103)

(3.104)

unde:

este numarul Reynolds. (3.105)

Miscarea perturbata

Se considera o miscare de baza paralela peste care se suprapun perturbatiile u , v , w , p . N marimi adimensionale, cu notatii fara bare,

Perturbatiile vor satisface sistemul:

^(3.106)

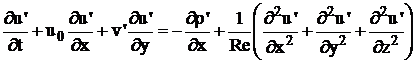(3.107) ^(3.108)

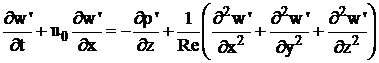(3.109)

Pe cele doua suprafete solide plane (y = 0,1) perturbatiile vitezei se considera nule.

Sistemul (3.106) (3.109) admite solutii de forma:

(3.110)

(3.111)

(3.112)

, (3.113)

unde functiile amplitudine sunt marimi complexe; a b si c sunt de asemeni marimi complexe.

Notam cu D = d/dy, D2 = d2/d2y, introducem relatiile (3.110) (3.113) in ecuatiile sistemului (3.106) (3.109) si deducem sistemul:

, (3.114)

, (3.115)

, (3.116)

, (3.117)

cu mentiunea ca pe suprafetele solide plane amplitudinile sunt nule.

C.C. Lin transforma sistemul (3.114) . (3.117) intr-un sistem omogen de sase ecuatii de ordinul intai cu sase necunoscute, cuprinse in matricea coloana (X):

. (3.118)

Forma matriceala a sistemului omogen (3.114) (3.117) este:

, (3.119)

unde , A fiind matricea patrata:

(3.120)

unde: . Pe suprafetele solide plane ce delimiteaza fluidul avem:

x1 = x2 = x3 = 0.

Caracterizare a stabilitatii dupa H.B. Squire

O prima caracterizare a stabilitatii unei miscari de baza paralela si plana se obtine prin urmarirea evolutiei unor perturbatii bidimensionale.

Este valabila astfel teorema lui Squire:

"pentru o miscare paralela bidimensionala caracterizata printr-o distributie de viteze cel mai mic numar Raynolds critic apare pentru cazul unor perturbatii bidimensionale care se propaga in aceeasi directie x cu vitezele din miscarea de baza".

Ecuatia Orr-Sommerfeld

Se adopta perturbatiile de forma:

, (3.125)

, (3.126)

, (3.127)

denumite undele transversale Tallmien-Schlichting.

Pentru t finit fronturile de unda sunt suprafete cilindrice cu generatoarele paralele cu axa Oz, perpendiculare pe planul miscarii de baza.

Pentru determinarea perturbatiilor (3.125) (3.127), avem de rezolvat sistemul de trei ecuatii cu necunoscutele :

, (3.128)

, (3.129)

, (3.130)

cu conditiile la limita u = 0, v = 0 pe cele doua suprafete frontiera, sau sistemul de patru ecuatii cu patru necunoscute dedus din (3.114) (3.117) cu .

Sistemul (3.128) (3.130) este liniar, fapt care permite eliminarea a doua din cele trei necunoscute (), forma cea mai simpla fiind:

, (3.131)

cunoscuta sub numele de ecuatia Orr-Sommerfeld.

3.6.1 Problema nevascoasa

Unele rezultate se pot deduce studiind problema nevascoasa cu inlocuirea profilelor de viteze cu unele liniare pe portiuni. Se considera trei tipuri de variatii liniare [7, 16, 31, 49, 89, 109]:

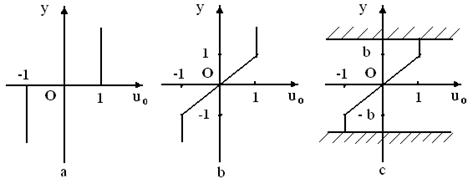
Fig. 3.2 Miscari de baza cu viteze liniare pe portiuni

Cazul (a) aproximeaza miscarea in prezenta unui strat de vartejuri, distributia din (b) inlocuieste un strat de forfecare de grosime finita in fluid nelimitat iar cel din (c) aproximeaza un strat de forfecare marginit de doua suprafete de fluid limitat. Se impune deducerea unei conditii de racordare pentru punctele in care u₀ sau prezinta o discontinuitate.

Prima conditie de racordare:

. (3.150)

A doua conditie de racordare se deduce din aspectul fizic de inexistenta a unui salt de presiune, scriind relatia (3.137) pentru sub forma:

, (3.151)

Miscarea este instabila sub forma unor unde stationare ce cresc proportional cu .

Pentru cazul din fig. 3.2.b,

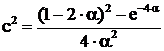(3.155) Din obtinem solutia , iar pentru rezulta c_i > 0 ceea ce conduce la instabilitate. Gradul maxim de amplificare se

obtine .

In cazul variatiei din fig.3.2.c, deoarece c² este o functie monoton crescatoare cu a, rezulta ca miscarea este instabila pentru b<

3.6.2 Problema vascoasa

Studiul conditiilor in care o miscare isi poate pierde stabilitatea, respectiv determinarea unui numar Reynolds critic, se face numai cu considerarea efectului vascozitatii. Se considera o miscare de baza paralela plana, pentru care este valabila ecuatia completa Orr-Sommerfeld (3.136). Aceasta ecuatie fiind de gradul patru si liniara, pentru constructia solutiei generale este suficient sa cunoastem patru solutii liniar independente, notate f f f f , iar solutia generala a ecuatiei (3.136) va fi:

, (3.158)

Conditia ca sistemul omogen (3.162) sa aiba solutii nenule este ca determinantul sistemului sa se anuleze:

, (3.163)

care reprezinta frontiera de stabilitate, deoarece putem deduce din aceasta perechile de valori , Re pentru care c_i = 0.

3.7 Instabilitatea termica

Mecanismul prin care se produce variatia densitatii este cel termic ca urmare a dilatarii unui fluid sub efectul incalzirii.

Instabilitatea termica apare in situatiile in care un lichid este incalzit in partea sa de jos. Cazul cel mai cercetat este un strat de lichid orizontal aflat pe o suprafata solida mai calda, cealalta suprafata de deasupra stratului de lichid, poate fi solida dar mai rece, sau poate fi o suprafata libera, in contact cu atmosfera, de asemenea mai rece. Efectul de tip Arhimede conduce la o forta verticala care modifica echilibrul static, invingand si efectele stabilizatoare ale vascozitatii si conductibilitatii termice [7, 16, 31, 49, 89, 109].

Rayleigh a formulat o teorie a instabilitatii convective a unui strat de lichid intre doua placi plane orizontale pentru fluide, denumite model Boussinesq, pentru care densitatea acestora variaza putin cu temperatura. Rayleigh a aratat ca instablitatea apare la depasirea unei valori critice a numarului Rayleigh (Ra):

, (3.171)

3.8 Ecuatiile generale pentru perturbatii

Se analizeaza un fluid Boussinesq (densitate aproape constanta), aflat in repaus care umple spatiul cuprins intre doua plane orizontale z = 0 si z = h, cu temperaturile T = si respectiv . Starea de baza a fluidului este caracterizata prin:

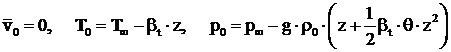, (3.179)

in domeniul , unde:

. (3.180)

De mentionat ca variatia liniara a temperaturii cu inaltimea z este o consecinta directa a ecuatiei energiei (3.177), deoarece din , rezulta , iar instabilitatea apare numai daca .

Se considera ca peste starea de baza caracterizata prin relatiile (3.175), (3.176), (3.177), (3.179) apar perturbatii mici de forma:

, (3.181)

care vor satisface sistemul:

, (3.182)

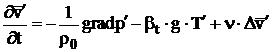(3.183)

(3.184)

CAPITOLUL 4

STABILITATEA FLACARILOR

DE GAZE COMBUSTIBILE IN JETURI TURBULENTE

4.1 Introducere

Combustibilii gazosi se ard de regula sub forma de flacara difuziva in jeturi turbulente sau turbionate. Procesul de ardere a combustibililor gazosi in jeturi turbulente de gaze este conditionat de o serie de factori geometrici, fizici si chimici a caror variatie conduc la modificarea starii flacarii respective. Diferitele stari de existenta a flacarii sunt prezentate in lucrarile de specialitate, in cadrul problemei generale a stabilitatii flacarii [24, 29, 35, 49, 89].

Pentru arzatoare de geometrie simpla, tub de sectiune circulara, rezulta diagrama din fig. 4.1 in care se identifica patru domenii:

stingere,

retur,

flacara suspendata,

flacara amorsata pe conturul sectiunii de iesire din arzator.

In abscisa este reprezentata concentratia combustibilului gazos in amestec cu aerul din jet, iar pe ordonata viteza initiala a jetului:

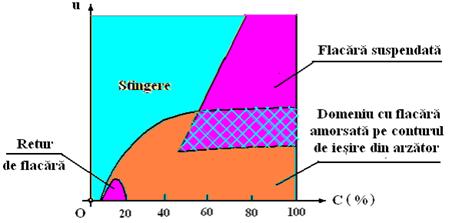
Fig. 4.1 Diagrama completa de ardere

Este de remarcat faptul ca in diagrama apare o zona in care se suprapun domeniul de stabilitate cu flacara suspendata, cu cel al flacarilor amorsate pe conturul sectiunii de iesire a jetului de combustibil gazos. Aceasta situatie se explica prin aceea ca, revenirea flacarii suspendate pe conturul sectiunii de iesire se produce la o viteza de curgere mai mica decat aceea la care se produce trecerea de la flacara amorsata pe conturul orificiului de iesire la cea suspendata.

4.2 Modelul fizic al conditiei de stabilitate a arderii

Pentru determinarea vitezei de rupere a flacarii difuziv turbulente, se porneste de la conditia de stabilitate a arderii, care este data de egalitatea vitezei de curgere a jetului cu viteza turbulenta maxima, in zonele in care este atinsa aceasta viteza. Viteza turbulenta de ardere , asa cum rezulta din tratatele de specialitate depinde de viteza normala de ardere , precum si de caracteristicile turbulentei. Cum viteza normala de ardere este maxima in concentratiile stoichiometrice, rezulta ca viteza maxima a vitezei turbulente de propagare a flacarii este atinsa in aceasta zona. Viteza normala de ardere este o caracteristica a combustibilului gazos respectiv si are o valoare foarte mica. De exemplu viteza normala maxima de ardere a gazului metan este 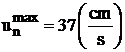[24, 35, 49, 89].

Flacara se misca in raport cu amestecul proaspat care se gaseste in curent cu viteza u_n si in raport cu gaze de ardere cu viteza u_ga, situatie in care gazele de ardere se misca fata de amestecul proaspat cu viteza (u_ga - u_n) (figura 4.2).

Fig. 4.2 Schema de propagare a flacarii intr-un amestec aer - combustibil

Din conditia ca din frontul de flacara caldura se transmite prin conductie si se consuma pentru incalzirea amestecului combstibil care intra in frontul de flacara, se obtine:

,    (4.6)

unde: j este factor subunitar, a - reprezinta difuzibilitatea termica iar t este timpul de reactie chimica in flacara. Se observa din relatia (4.5) ca nu depinde de viteza de degajare a caldurii care este functie de substantele in amestec si de temperatura.

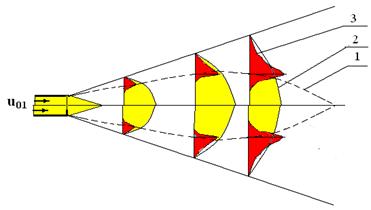
Fig. 4.3. Campul de viteze axiale, concentratiei si vitezelor de ardere:

1 - locul geometric al concentratiilor stoichiometrice; 2 - variatia vitezei axiale a jetului;

3 - variatia vitezei de ardere in jet.

4.3 Viteza de propagarea frontului de flacara in jeturi turbulente

In jeturile turbulente transferul de masa si de caldura fiind foarte mult intensificat fata de jeturile laminare, rezulta ca, in cazul arderii in jeturi turbulente viteza de propagare in regim turbulent este mult mai mare decat cea in regim laminar . In cazul flacarilor difuziv turbulente viteza turbulenta de ardere este functie de viteza laminara (normala) , precum si de caracteristicile turbulentei. In cazul curgerii cu scara mare a turbulentei viteza turbulenta de ardere depinde in special de componenta medie a pulsatiei vitezei , iar pentru regim cu scara mica a turbulentei de intensificarea schimbului de masa, recomandandu-se urmatoarele formule de calcul [24, 29, 35, 49, 89]:

- pentru scara mare a turbulentei:

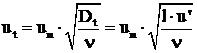, (4.7)

pentru scara mica a turbulentei:

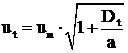, (4.8)

in care este coeficientul de difuzie turbulenta, - coeficientul cinematic de vascozitate al amesteculului, l - scara turbulentei, - intensitatea turbulentei, a - coeficientul de difuzivitate a temperaturii.

Coeficientul de difuzie turbulenta se poate calcula cu relatia:

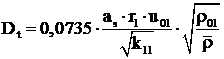, (4.9)

unde:

- este coeficientul de structura al jetului, care depinde de unghiul de evazare a jetului. Legatura dintre coeficientul de structura al jetului "a" si unghiul a, de evazare a jetului este data de relatia:

(4.10)

Avind in vedere ca viteza turbulenta maxima are loc in zona concentratiilor stoichiometrice, aceasta viteza se poate determina cu relatia:

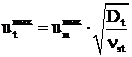, (4.13)

in care reprezinta vascozitatea cinematica la amestec stoichiometric.

Functiile universale de distributie a vitezelor, concentratiilor si temperaturilor in sectiunile de baza ale jeturilor turbulente cu viteza ambianta nula sunt:

,

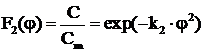, (4.15)

,

in care u este viteza intr-un punct oarecare dintr-o sectiune transversala din zona de baza a jetului ; viteza jetului pe axa acestuia in aceeasi sectiune; C - concentratia in punctul de coordonate (x , y) al unei sectiuni transversale din zona de baza a jetului; - concentratia pe axa jetului, in aceeasi sectiune; T, - temperaturile in punctul de coordonate (x , y) si respectiv pe axa jetului, in aceeasi sectiune; - temperatura la granita jetului.

4.4.1 Determinarea variatiei vitezei in lungul axei jetului

Studiu de caz 4.1

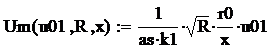
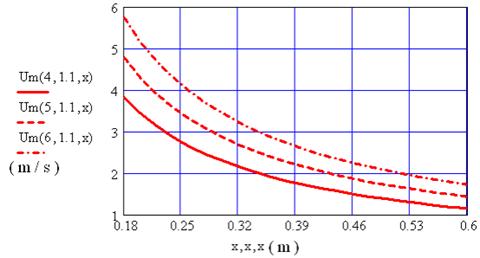
Fig. 4.6 Variatia vitezei jetului in lungul axei in functie de vitezele initiale

4.4.2 Determinarea variatiei concentratiei amestecului in lungul axei jetului

Avind in vedere functiile si relatia (4.28) se poate scrie sub forma:

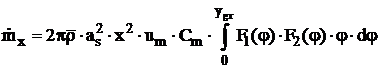. (4.29)

Legea de variatie a concentratiei a jetului axial simetric in lungul axei:

, (4.31)

unde .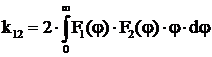

Studiu de caz 4.2

Variatia concentratiei in jetul axial simetric:

Fig. 4.7 Variatia concentratiei in lungul axei jetului in functie de factorul R

4.4.3 Determinarea vitezei de rupere a flacarii in jet turbulent axial simetric cu viteza ambianta nula

Viteza initiala a jetului , pentru care este indeplinita conditia , este considerata viteza de rupere a flacarii . Domeniul de stabilitate al flacarii este dat pentru viteze initiale [24, 29, 35, 49, 89].

Conditia , corespunde punctului in care pe axa jetului se realizeaza concentratia stoichiometrica. Experimentele efectuate pentru determinarea vitezei de rupere arata ca, in apropierea momentului de rupere, apar pulsatii mari ale flacarii, dupa care aceasta dispare.

Din relatiile (4.9) si (4.13), scrise pentru punctul de pe axa jetului in care se realizeaza concentatia stoichiometrica, prin ridicare la patrat, rezulta:

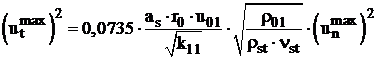. (4.32)

Viteza pe axa jetului, la distanta , se poate determina din relatia (4.24), rezultand:

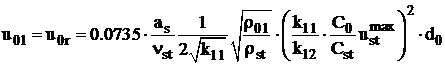, (4.38)

in care este diametrul orificiului de evacuare al jetului.

Din analiza relatiei (4.38), se constata ca flacarile in jeturi de gaze combustibile cu preamestec (), au domeniul de stabilitate mai redus decit cele fara preamestec.

4.5 Domeniul de stabilitate al flacarilor difuziv turbulente in jeturi libere axial simetrice de gaze combustibile cu viteza ambianta variabila

In cazul jeturilor turbulente cu viteza ambianta variabila este de facut unele observatii in legatura cu functia de distributie a vitezelor in sectiunile transversale din zona de baza a jetului. Pentru a putea face aceste observatii, este necesar a se prezenta structura unui astfel de jet, mai ales ca in marea majoritate a arzatoarelor de gaze combustibile se intalneste acest caz [24, 29, 35, 49, 89].

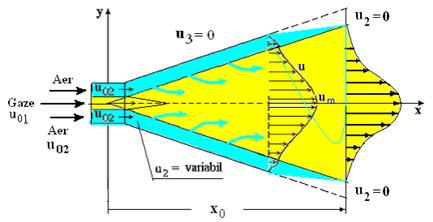
Fig. 4.8 Cimpul de viteze in jetul turbulent axial simetric cu viteza ambianta variabila

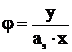Din analiza figurii 4.8 se constata ca, de la o anumita distanta , ansamblul celor doua jeturi se comporta ca un jet liber, cu viteza ambianta nula, pentru care , fiind constant: daca sau daca se adopta . Incepand de la , In cazul in care , depinde de distanta x, astfel ca . Ca si in cazul jeturilor cu viteza ambianta nula si in acest caz se porneste de la legea conservarii impulsului in lungul axei jetului cu viteza ambianta variabila, rezultand:

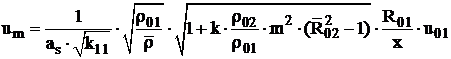. (4.47)

4.5.3 Domeniul de stabilitate al flacarilor difuziv turbulente in jeturi de gaze combustibile cu viteza ambianta variabila

Domeniul de stabilitate al flacarilor difuziv turbulente in jeturi de gaze combustibile cu viteza ambianta variabila este dat de relatia [24, 29, 35, 49, 89]:

, (4.54)

in care este viteza pe axa jetului in punctul in care concentratia este cea stoichiometrica; reprezinta viteza de propagare a flacarii in punctul in care pe axa concentratia devine .

Din relatia (4.47) se poate determina sub forma:

. (4.55)

Tinand seama de relatia (4.36) care exprima viteza de rupere in cazul flacarilor in jeturi cu viteza ambianta nula (), se poate scrie:

, (4.61)

in care:

- este viteza inferioara a jetului pentru care flacara se rupe:

; (4.62)

- este viteza superioara de rupere a flacarii la aceeasi viteza initiala a aerului :

. (4.63)

Domeniul de stabilitate al flacarii in jet de gaze combustibile cu viteza ambianta nula este o parabola, reprezentata in fig. 4.9:

Fig. 4.9 Domeniul de stabilitate al flacarilor in jeturi libere axial

simetrice cu viteza ambianta variabila

Din analiza fig. 4.9 se constata ca, pe masura ce viteza aerului creste, domeniul de stabilitate al flacarii se ingusteaza, ajungand la o anumita viteza a aerului , ca cele doua viteze si sa se confunde:

.

Studiu de caz 4.3

Se determina polinoamele de regresie, utilizand metoda celor mai mici patrate, pentru:

curba ;

curbele si .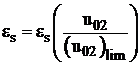

si rezulta, pentru curba , polinomul:

. (4.66)

Reprezentarea grafica functiei (4.65) este data in fig. 4.12

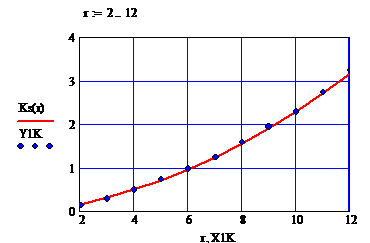
Fig. 4.12 Variatia coeficientului in functie de raportul ,data de functia

Se aplica acelasi algoritm pentru determinarea polinoamelor de regresie ale graficelor din fig.4.10. si obtinem:

, (4.67)

, (4.68)

cu urmatoarea reprezentare grafica:

Fig. 4.13 Variatia coeficientilor si in functie de raportul data

de functiile polinomiale Ei(u )si Es(u)

Program mathcad pentru calculul domeniului de stabilitate

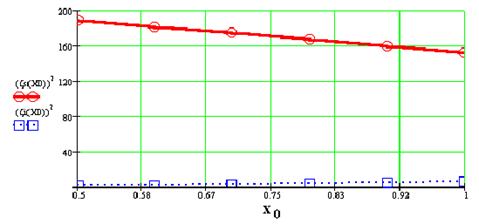
Fig. Sc.4.4.4 Limitele domeniului de stabilitate a flacarilor difuzive

Fig. Sc.4.4.6 Dependenta vitezei de rupere

a flacarii cu temperatura aerului preincalzit

4.7.1 Viteza turbulenta maxima a flacarii in jet turbionat

Componenta axiala a vitezei initiale a jetului turbionat , la care are loc ruperea (stingerea)flacarii se numeste viteza de rupere a flacarii. Criteriul de stabilitate, ca si in cazul flacarilor in jeturi neturbionate este cel legat de egalitatea

dintre viteza de curgere si cea de propagare a frontului de flacara [24, 29, 35, 49, 89].

Viteza turbulenta de ardere depinde de viteza normala de ardere , care este maxima in zona concentratiilor stoichiometrice.

In aceasta situatie, viteza turbulenta maxima va fi in zona concentratiilor stoichiometrice, conform reprezentarii din fig. 4.15:

Fig. 4.15 Variatia vitezei turbulente de ardere in zona de baza a 1 - locul geometric al concentratiilor stoichiometrice; 2 - variatia vitezei axiale in zona de baza a jetului;

3 - variatia vitezei turbulente de ardere

In cazul jeturilor turbionate, pentru coeficientul de difuzie turbulenta relatia:

. (4.75)

4.7.2 Determinarea variatiei vitezei axiale in lungul axei jetului turbionat

Pentru determinarea acestei variatii se utilizeaza ecuatia conservarii impulsului axial, in zona de baza a jetului, care se scrie astfel [24, 29, 35, 49, 89]:

, (4.76)

Este de remarcat ca in literatura tehnica de specialitate s-a adoptat pentru functia , , unde 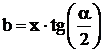este semigrosimea jetului in sectiunile de baza ale acestuia.

Introducand pe 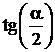, conform relatiei (4.74) se obtine:

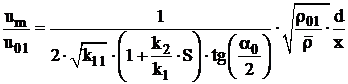. (4.79)

4.7.3 Determinarea variatiei concentratiei in lungul axei jetului in zona de baza a jetului turbionat

Determinarea acestei variatii se face prin utilizarea ecuatiei conservarii masei initiale de combustibil, adica [24, 29, 35, 49, 89]:

, (4.80)

Daca se noteaza cu si se tine seama de relatia (4.79), dupa unele transformari din relatia (4.80) se obtine:

. (4.81)

4.7.4 Determinarea vitezei de rupere a flacarii

Din relatia (4.81) se poate determina , la care se realizeaza pe axa jetului concentratia stoichiometrica. Astfel rezulta [24, 29, 35, 49, 89]:

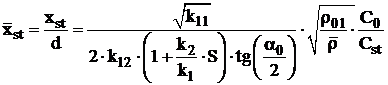. (4.82)

Se constata ca :

. (4.87)

Daca se considera arderea in jet moderat turbionat, cu parametrul turbionului S = 0,4 si unghiul si tinand seama de valorile lui si , se obtine pentru raportul 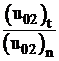, valoarea:2,879.

Din analiza relatiei (4.85), se constata ca viteza de rupere a flacarilor difuziv turbionate in jeturi de gaze combustibile depinde de parametrul turbionului S, crescand odata cu marirea acestuia, fapt ce permite viteze de curgere mari, in comparatie cu flacarile in jeturi neturbionate.

Din relatia (4.87), aplicata unui jet turbionat moderat cu coeficientul turbionului S = 0,4, rezulta ca domeniul de stabilitate al flacarii in jet turbionat este de 2,879 ori mai mare decat al unei flacari in jet neturbionat.

CAPITOLUL 5

APLICAREA METODELOR NUMERICE IN STUDIUL

ARDERII DIFUZIVE A COMBUSIBILILOR GAZOSI

5.1 Metoda modelarii fractiei de amestec/PDF (Probability Density Functions)

Metoda modelarii fractiei de amestec / PDF a fost dezvoltata pentru simularea flacarilor difuziv turbulente si a proceselor de reactie similare in care turbulenta furnizeaza o limitare a vitezei reactiei chimice. Pentru astfel de sisteme, metoda PDF ofera multe beneficii in raport cu formularea vitezei finite. Metoda fractiei de amestec permite modelarea formarii compusilor chimici intermediari, a efectelor disocierii, si permite luarea in considerare intr-un mod riguros a cuplajului dintre turbulenta si reactia chimica [5, 14, 35, 44, 67, 121].

Mecanismele de reactie, care pot fi necunoscute sau extrem de complexe, nu sunt definite explicit, in locul acestora, in sistemul reactant se utilizeaza:

reactia chimica infinit de rapida (stratul de flacara, sau conceptul "amestecat ars");

calcule de echilibru chimic;

- calcule de neechilibru (fasiile de flacara).

Metoda modelarii fractiei amestecului se bazeaza pe un set de ipoteze simplificatoare, iar starea termo - chimica instantanee a fluidului este raportata la o cantitate scalara ce se conserva in timpul procesului chimic, denumita fractia amestecului, . Pentru un sistem binar, constand din combustibil si oxidant, fractia amestecului poate fi scrisa in termenii participatiei masice elementare sub forma:

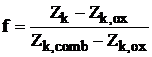(5.1)

unde este participatia masica elementara pentru un element k . Indicele inferior "ox" indica valoarea participatiei masice a elementului " k " la intrarea curentului de oxidant in domeniul de analiza, iar indicele inferior "comb", indica valoarea participatiei masice a elementului " k ", la intrare in domeniul de analiza a curentului de combustibil. Pentru sisteme complexe combustibil-oxidant, fractia amestecului poate fi definita mai simplu ca participatie masica locala a combustibilului, unde prin "combustibil" se intelege intreg amestecul de substante ce joaca rol de combustibil pentru reactia de ardere in problema analizata. Astfel, in cazul in care curentul de combustibil contine CH₄ si CO, "participatia masica locala a combustibilului" este reprezentata de participatia masica a amestecului de combustibili (CH₄ si CO) si nu doar de participatia masica a CH₄. Daca curentul secundar (reprezentand un alt combustibil, alt oxidant sau un fluid nonreactant) este inclus in calcule, combustibilul si fractiile de amestec secundar sunt reprezentate de participatiile masice ale combustibilului si ale curentilor secundari. Suma tuturor celor trei fractii de amestec din sistem (combustibilul, curentul secundar si oxidantul) este totdeauna egala cu unitatea:

(5.2)

Aceasta indica, conform figurii 5.2 a, ca doar punctele din planul ABC in spatiul fractiei amestecului sunt valabile. In consecinta, cele doua fractii ale amestecului, si , nu pot varia independent: valorile lor sunt corecte doar daca ele vor fi situate in acelasi timp in interiorul triunghiului OBC din figura 5.2. b.

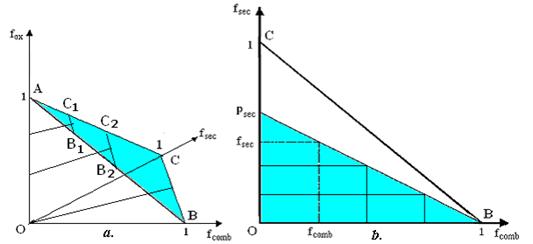
Fig. 5.2 Relatia dintre , si

5.1.4 Modele pentru abordarea echilibrului chimic in arderile

nepreamestecate

Abordarea pentru o singura fractie de amestec

Pentru a mentine timpul de calcul la minimum, majoritatea calculelor necesare pentru modelul arderii nepreamestecate, sunt realizate in afara Fluentului, prin procesarea calculelor chimiei si a integrarii PDF intr-un cod separat, numit prePDF. In figura 5.9 este ilustrat cum este impartit calculul intre preprocesor (prePDF) si rezolvitor (FLUENT). In prePDF, modelul chimiei (amestecat este ars, echilibrul chimic sau flacari laminare) este folosit impreuna cu forma asumata a PDF, pentru a realiza integrarea ecuatiilor (5.15), (5.17), si/sau (5.24). Aceste integrale sunt calculate cu prePDF si memorate in tabele care descriu variatia valorilor medii termochimice (temperatura, densitatea si fractiile masice ale speciilor) in functie de valorile , si .

De notat ca varianta fractiei de amestec este folosita pentru obtinerea de date sub forma de tabele, unde

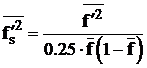(5.28)

Date sub forma de tabele pentru sisteme adiabate

Conceptul de tabela generata de prePDF,se refera la un sistem cu o singura fractie de amestec. Ea furnizeaza Fluent-ului valorile pentru si intr-un punct din domeniul de curgere, valorile mediate in timp ale fractiilor masice, densitatii si temperaturii (). Fluent foloseste ecuatia (5.28) pentru a calcula varianta medie a fractiei de amestec intrucat tabela fractiei de amestec contine datele corespunzatoare .

Tabela este rezultatul matematic al integrarii ecuatiei (5.17). Se calculeaza o tabela pentru fiecare scalar (fractia masica a speciilor, densitatea, temperatura). In sistemele adiabatice, unde entalpia instantanee este functie doar de fractia de amestec instantanee, se determina o tabela cu doua dimensiuni.

Fig. 5.9 Modul de calcul al programului FLUENT si prePDF

pentru o fractie de amestec

Pentru un sistem cu doua fractii de amestec, se vor determina valorile instantanee ale temperaturii, densitatii si a fractiilor masice ale speciilor (ecuatiile 5.10 sau 5.13) si se vor memora in tabelele corespunzatoare. Pentru cazul sistemului adiabatic cu doua fractii de amestec tabelele cuprind , si ca functie de fractia de amestec a combustibilului si de fractia secundara partiala (fig. 5.10).

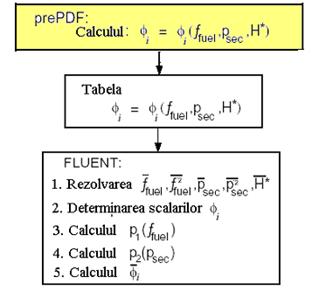
Fig. 5.10 Modul de calcul al programului FLUENT si prePDF

pentru doua fractii de amestec

5.2 Modelare numerica cu metoda volumului finit

5.2.1 Arhitectura configuratiei analizate

Se considera cazul a trei duze cu axele in acelasi plan (fig. 5.11). Diametrul duzelor este de 5 mm iar distanta dintre axe este de 10 cm. Prin duze curge gaz cu viteza de 20 m/s. Duzele sunt pozitionate in curent de aer cu viteza de 1 m/s. Distributia vitezelor pe sectiunile de intrare a gazului si a aerului se considera constanta.

Pentru studiul curgerii se considera un domeniu cilindric cu baza eliptica, cu dimensiunile prezentate in figura 5.12.

   

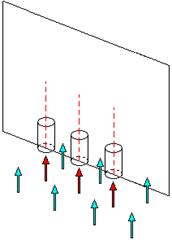
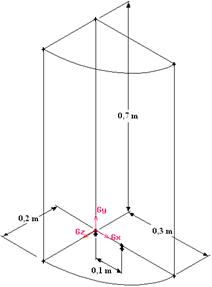
Fig. 5.11 Domeniu cilindric Fig. 5.12 Geometria domeniului cilindric

5.2.2 Discretizarea domeniului si tabelele fractiilor de amestec

Domeniul s-a discretizat cu elemente tetraedrale. In figura 5.13 se prezinta fetele celulelor pe planele de simetrie si pe sectiunile de intrare.

Fig. 5.13 Discretizarea domeniului (fetele elementelor pe planele de simetrie,

pe intrarile in domeniu si pe pereti)

Tabelele calculate pentru temperatura, densitate, fractii molare ale speciilor sunt prezentate in figurile 5.14-5.20.

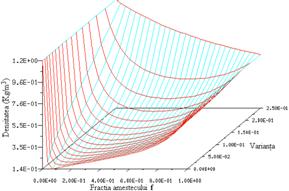
Fig. 5.14 Tabela PDF - temperatura. Fig. 5.15 Tabela PDF - densitatea.

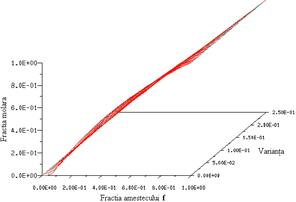
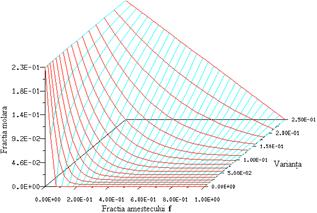
Fig. 5.16 Tabela PDF - fractia molara CH₄ Fig. 5.17 Tabela PDF - fractia molara O₂

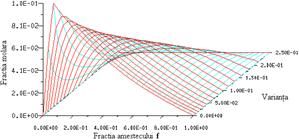
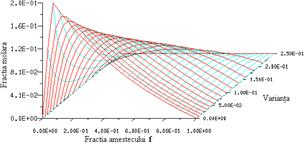
Fig. 5.18 Tabela PDF - fractia molara CO₂ Fig. 5.19 Tabela PDF - fractia molara H₂O

5.2.3 Rezultate obtinute prin modelare cu metoda volumului finit

In urma calculelor numerice, a rezultat o variatie a campului vitezelor pe cele doua plane de simetrie, prezentate in figura 5.21 si 5.22 si o variatie a campului temperaturilor prezentate in figura 5.23 si 5.24.

In figurile 5.25 - 5.32 sunt prezentate campurile de fractii masice ale speciilor , , si , pe cele doua plane de simetrie ale domeniului.

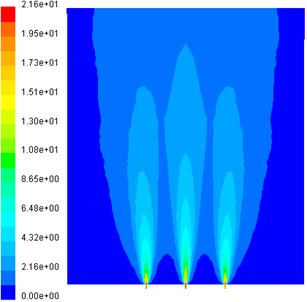
Fig. 5.21 Campul de Fig. 5.22 Campul de

viteze pe planul de simetrie 1 viteze pe planul de simetrie 2

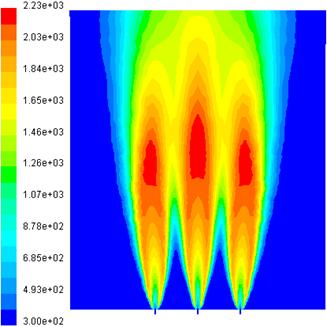
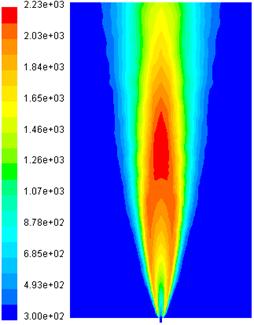
Fig. 5.23 Campul de temperaturi Fig. 5.24 Campul de temperaturi

pe planul de simetrie 1 pe planul de simetrie 2

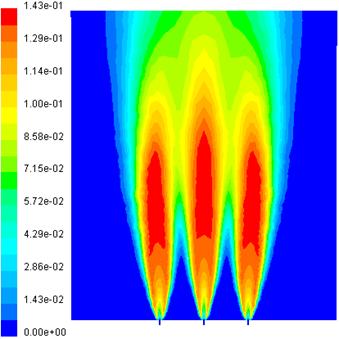
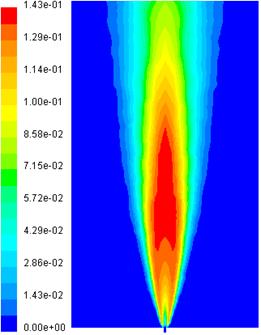
Fig. 5.27 Campul de fractii masice Fig. 5.28 Campul de fractii masice

de CO₂ pe planul de simetrie 1 de CO₂ pe planul de simetrie 2

5.2.4 Grafice ale variatiei vitezelor si temperaturilor

In figura 5.33 sunt prezentate variatiile vitezei dupa axa duzei centrale (cu negru) si dupa axa unei duze laterale (cu rosu). Considerand trei directii orizontale aflate in planul axelor celor trei duze, in figura 5.34 sunt prezentate variatiile vitezei dupa cele trei directii. Ordonata este masurata din dreptul axei duzei centrale.

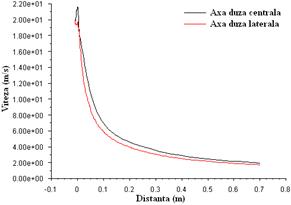
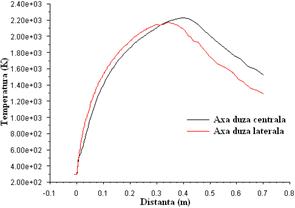
Fig. 5.33 Variatia vitezelor dupa Fig. 5.35 Variatia temperaturilor

axele duzei centrale si laterale dupa axele duzei centrale si laterale

CAPITOLUL 6

CERCETARI EXPERIMENTALE, MODELARI NUMERICE SI PRELUCRARI STATISTICE

6.1 Instalatia experimentala

Cercetarile experimentale au fost efectuate la U.P.B., in laboratorul de arderea combustibilului gazos al catedrei de echipament termic si nuclear. Instalatia contine un ventilator (fig.6.1) montat la unul din capetele unui tronson cu sectiune dreptunghiulara, prevazut la al doilea capat cu doua stuturi (1 si 2) pentru masurarea debitului de aer produs de ventilator si un corp cilindric pentru fixarea in interior a arzatoarelor.

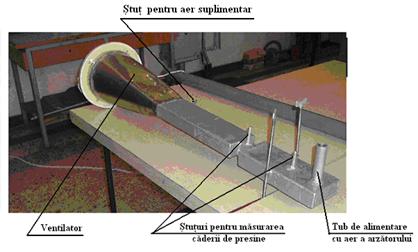
Fig. 6.1 Instalatie experimentala

Fig. 6.3 Arzatoare utilizate pentru studiul stabilitatii flacarilor difuzive

6.2 Schema arzatorului

Aerul provine de la un ventilator sau de la un compresor atasat instalatiei experimentale. Caracteristicile ventilatorului sunt:

P = 20 W, n = 1900 rot/min., = 200 mm H₂O.

Pentru analiza stabilitatii flacarii la actiunea laterala a unui jet de aer, provenit de la compresor, se fixeaza in dreptul arzatorului un ajutaj cu sectiunea dreptunghiulara 27 4 . Pentru fiecare tip de arzator au fost efectuate, pentru diferite debite de gaz metan si aer, masurari pentru urmatoarele marimi:

- debitul de gaz metan;

- temperatura gazului metan;

- presiunea gazului metan;

- debitul de aer;

- temperatura aerului;

- presiunea aerului;

- lungimea flacarii;

- lungimea de acrosare a flacarii;

- debitul de gaz metan la care flacara s-a rupt.

Diametrul de iesire al aerului insotitor .

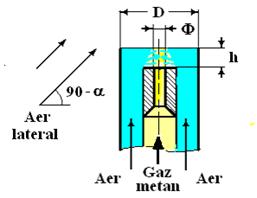
Fig. 6.4 Schema cu pozitia duzei

Debitele de gaz metan au fost determinate cu ajutorul unui rotametru etalonat pentru aer la temperatura de 10 C si presiune normala.

Experimentarile au fost efectuate pentru flacari deschise.

Presiunea si temperatura gazului metan in timpul experimentelor: ; .

6.3.1 Diametrul duzei - ardere fara aer

►

Fig. 6.6 Lungimile flacarilor la ardere fara aer prin duza

Valorile medii pentru

Polinoame de regresie pentru lungimea flacarilor difuzive la fara aer principal. Program in Mathcad

lungimea flacarilor difuzive (), rezulta:

Fig. 6.8.1 Polinom de regresie pentru lungimea flacarilor difuzive ()

lungimea flacarilor difuziv cinetice (), rezulta:

Fig. 6.8.2 Polinom de regresie pentru lungimea flacarilor difuzive ()

lungimea flacarilor difuzive, partial cinetice (), rezulta:

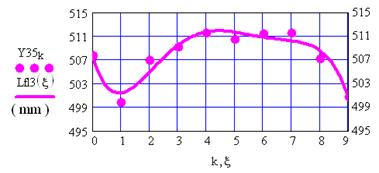
Fig. 6.8.3. Polinom de regresie pentru lungimea flacarilor difuzive ()

6.3.4 Analiza datelor experimentale la arderea difuziva (h = 0). Stabilirea a doua criterii de similitudine

Prin analiza dimensionala se stabilesc doua criterii de similitudine pentru lungimea flacarilor difuzive:

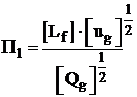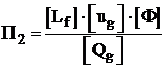, . (6.1)

Valorile numerice ale criteriilor de similitudine se obtin cu datele din matricea Data1 sub forma:

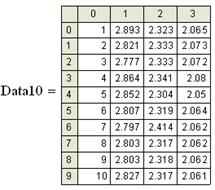
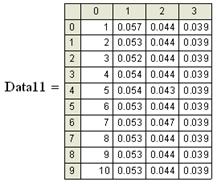
unde pe coloanele 1,2,3 sunt valorile numerice ale criteriilor si , care dupa medierea aritmetica, devin

, respectiv . (6.2)

Lungimile flacarilor difuzive se pot calcula cu relatiile:

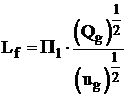, respectiv 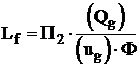, (6.3)

unde este diametrul duzei.

6.4.1 Diametrul duzei - ardere cu aer de la ventilator

►

Fig. 6.10 Lungimile flacarilor la ardere cu aer axial de la ventilator prin duza

Valorile medii pentru . Aer de la ventilator

6.5 Stabilitatea flacarilor in aer liber la actiunea jetului de aer lateral

Fig. 6.12 Flacara cu jet lateral de aer Fig. 6.13 Flacara instabila cu jet lateral de aer

6.5.1 Flacara fara aer principal si cu jet lateral de aer

6.6 Modelari numerice

Se considera cazul arderii gazului metan intr-o instalatie schematizata in figura 6.14. Conducta de gaz metan are un diametru exterior de 10 mm si unul interior de 7 mm. Diametrul duzei este de 5 mm. Conducta aerului principal are un diametru interior de 20 de mm si unul exterior de 24 mm, fiind coaxiala cu

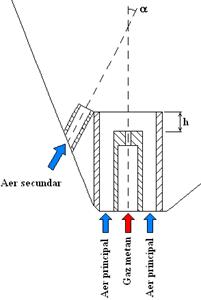
Fig. 6.14 Modul de intrare a gazului metan si a aerului in domeniu

Procesele chimice, curgerea gazelor si geometria prezinta acelasi plan de simetrie (prezentat in figura 6.15 cu galben). Domeniul de analiza si impartirea in celule tetraedrale sunt prezentate in figura 6.15. In figura sunt reprezentate fetele celulelor de pe suprafetele domeniului astfel: Cu galben fetele de pe planul de simetrie, cu rosu fetele de pe suprafata de iesiere din domeniu, cu negru fetele de pe suprafetele considerate pereti, iar cu albastru fetele de pe suprafetele de intrare in domeniu a gazului metan si a aerului. Domeniul este completat prin simetrie.

Se determina numeric patru cazuri:

duza este la nivelul conductei de aer principal (h = 0), se alimenteaza cu aer primar (caz 1)

duza este la nivelul conductei de aer principal (h = 0), se alimenteaza cu aer secundar (caz 2)

duza este la h = 25 mm sub iesirea conductei de aer principal, se alimenteaza cu aer primar (caz 3)

duza este la h = 25 mm sub iesirea conductei de aer principal, se alimenteaza cu aer secundar (caz 4)

Debitul de gaz este de 0,7 Nm³/h, iar cel de aer primar sau secundar este de 7 Nm³/h. Aceasta corespunde unei viteze medii de 5.05 m/s a gazului in conducta, unei viteze medii de 8.25 m/s a aerului principal si unei viteze medii de 17,36 m/s a aerului secundar. Caldurile specifice ale componentelor de reactie se considera variabile cu temperatura absoluta, legile de variatie fiind functii polinomiale de gradul 4.

Regimul de curgere se considera turbulent, modelul de turbulenta ales fiind k - e. Fenomenul de ardere este considerat stationar. Pentru modelarea arderii s-a considerat o ardere volumetrica, modelul ales fiind cel de disipare a vartejurilor.

Fig. 6.15 Impartirea cu celule a domeniului

6.6.2 Cazul 1

Viteza medie de intrare a gazului este de 5,05 m/s. Viteza de intrare a aerului principal este de 8.25 m/s. Viteza aerului secundar este 0 m/s. Duza este pozitionata la capatul galeriei aerului principal.

In urma determinarilor a rezultat o variatie a campului temperaturilor pe planul de simetrie, prezentat in figura 6.16 si o variatie a campului vitezelor in planul de simetrie prezentata in figura 6.17.

In figurile 6.18, 6.19, 6.20 si 6.21 sunt prezentate campurile de fractii masice ale speciilor , , si .

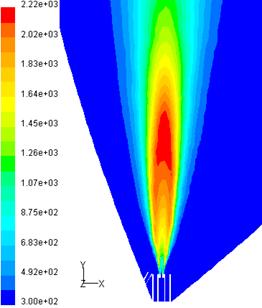
Fig. 6.16 Temperatura pe planul de simetrie Fig. 6.17 Viteza pe planul de simetrie

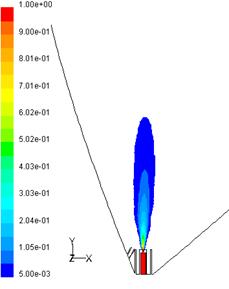
Fig. 6.18 Concentratia de Fig. 6.19 Concentratia de

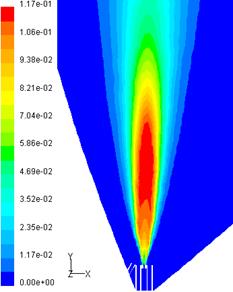
Fig. 6.20 Concentratia de Fig. 6.21 Concentratia de

In figurile 6.24 si 6.24 sunt prezentate variatiile temperaturii si ale vitezei in lungul axei oy.

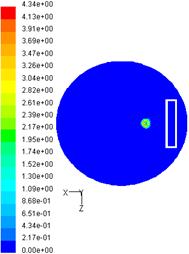
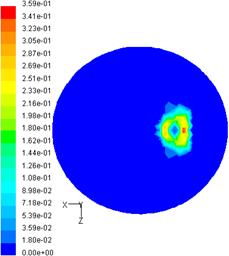
a)    b)

c) d)

Fig. 6.23 Distributia vitezei de reactie kmol/sec pe planul de simetrie

a)      la suprafata duzei; b) la 20 mm de suprafata duzei

c) la 40 mm de suprafata duzei; d) la 60 mm de suprafata duzei;

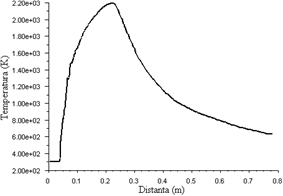
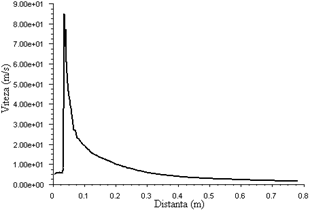
Fig. 6.24 Variatia temperaturii Fig. 6.25 Variatia vitezei

CAPITOLUL 7

CONCLUZII SI CONTRIBUTII

7.1 Concluzii

Dintre caracteristicile flacarilor difuzive, o importanta deosebita, pentru buna desfasurare a proceselor tehnologice, o prezinta cele legate de lungimea, stabilitatea si radiatia flacarilor.

Flacarile combustibililor gazosi au un coeficient de emisie a radiatiei termice foarte scazut, el datorandu-se numai gazelor triatomice, ceea ce impune ca in cazul folosirii arderii combustibilor gazosi in instalatii, la care procesul tehnologic solicita un transfer de caldura preponderent prin radiatie, este necesar a se trece la carburarea flacarii, fie prin aport de combustibil lichid (pacura) sau prin autocarburare.

Caracteristicile flacarilor difuzive din spatii finite (lungime, stabilitate si radiatie), vor depinde, atat de debitul de gaze recirculate, cat si de lungimea zonei de recirculare, care la randul lor sunt puternic influentate de parametrul aerodinamic si geometric al celor doua jeturi, cat si de caracteristicile geometrice ale ansamblului camera de ardere - jeturi.

Pentru studiul caracteristicilor flacarilor difuzive din spatii finite, este necesar a se lua in considerare nu numai arzatorul propriu-zis, ci intregul ansamblu arzator-camera de ardere, deoarece, cu acelasi arzator se pot realiza flacari cu caracteristici diferite in functie de dimensiunile si geometria camerei de ardere. Toate acestea conduc la concluzia ca, pentru a putea determina caracteristicile flacarilor difuziv turbulente, atat in cazul jeturilor libere, cat si in cazul flacarilor in jeturi din spatii finite, este necesar a cunoaste influenta diferitilor factori asupra procesului de amestecare dintre cele doua jeturi, putand astfel dirija acest proces, astfel incat sa se obtina flacari cu caracteristici impuse de necesitatile proceselor tehnologice.

In cazul flacarilor difuzive din spatii finite, fenomenul de recirculare externa a gazelor de ardere, prin debitul de gaze recirculate, catre baza flacarii, conduce la vicierea amestecului de gaze combustibile-aer, din incinta focarului, ceea ce conduce pentru aceleasi conditii initiale ale jetului de gaze combustibile, la o crestere a lungimii flacarii, fata de cea a flacarii in jet liber de gaze. In ceea ce priveste marimea acestei cresteri, parerile diversilor cercetatori sunt impartite.

Debitul de gaze recirculate extern au doua efecte asupra procesului de ardere, unul pozitiv benefic, prin aceea ca aduce un aport de caldura in zona amestecului combustibil-aer, ceea ce face ca viteza de propagare a frontului de flacari sa creasca, iar cel de al doilea negativ, deoarece gazele de ardere viciaza amestecul proaspat combustibil-aer, ducandu-l spre concentratii mai mici, deci spre viteze de ardere mai mici, sau chiar scotandu-l in afara limitelor de ardere.

Debitul de gaze de ardere, depinde de un parametru numit parametru de recirculare, care are expresia:

in care: C 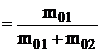este concentratia amestecului total intre debitul de combustibil m₀₁ si debitul de aer m₀₂; r₀ - raza duzei de iesire a jetului de gaze combustibile; = densitatea initiala a gazelor combustibile, la intrare in incinta de ardere. = densitatea gazelor de ardere la temperatura flacarii; L - raza echivalenta a camerei de ardere.

Este de remarcat faptul ca, in cazul instalatiilor de ardere care utilizeaza combustibili superiori, adica, cu putere calorica mare, debitul de gaze recirculate extern este mult mai mic, decat in cazul utilizarii combustibililor inferiori, acest lucru putand fi explicat prin aceea ca, in cazul combustibililor superiori aerul necesar arderii unui kilogram de combustibil este mult mai mare decat cel necesar pentru un kilogram de combustibil inferior, astfel ca, lungimea necesara difuziei jetului de aer in jetul de combustibil pentru combustibilul superior este mai mare, ceea ce face ca lungimea zonei de recirculare externa a gazelor de ardere sa fie mai mica, iar in unele cazuri inexistenta, cazuri in care pentru lungimea si stabilitatea flacarilor se poate utiliza teoria jeturilor turbulente libere.

Un prim domeniu de flacara stabila este acela la care flacara este amorsata direct pe conturul sectiunii de iesire a arzatorului, unde se indeplinesc conditiile necesare stabilirii unui front de flacara, adica egalitatea vitezei de propagare a frontului de flacara cu cea a jetului de gaze, precum si absorbtia de catre jet a unei cantitati de aer, necesara realizarii unei concentratii la care procesul poate avea loc.

Un alt domeniu de ardere stabila este cel al flacarilor difuzive, asa zise "suspendate", la care flacara se amorseaza stabil la o anumita distanta de gura de iesire a jetului din arzator, adica la o distanta la care se realizeaza egalitatea dintre viteza de curgere si viteza turbulenta de propagare a frontului de flacara.

In afara de aceste doua domenii de ardere stabila, exista un domeniu la care flacara nu mai este stabila in nici o zona a jetului. Viteza initiala a jetului de gaze combustibile, la care apare acest domeniu, este cunoscut in literatura de specialitate, ca viteza de rupere a flacarii.

Jeturile turbulente pot fi clasificate in doua grupe mari:

• Jeturi turbulete libere:

cu viteza ambianta nula (u₂ = 0);

cu viteza ambianta constanta (u₂ = const.);

cu viteza ambianta variabila (u₂ = variabil).

• Jeturi turbulente marginite

cu viteza ambianta constanta (u₂ = constant);

cu viteza ambianta variabila (u₂ = variabil).

Pentru determinarea schimbului de masa si de caldura, se stabilesc functiile universale ale distributiei vitezelor, concentratiilor si temperaturilor in zona de baza a jetului, care au expresiile:

; ; .

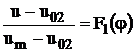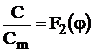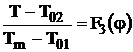Variatia vitezei pe axa jetului in conditiile:

viteza principala: u01 , viteza secundara: u02 = 2 are urmatoarea reprezentare grafica:

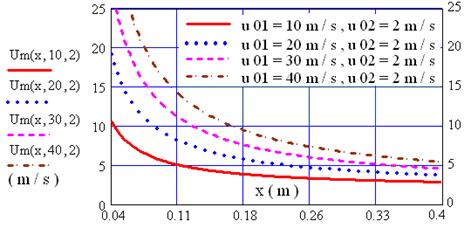
Pentru valori (unde u_m reprezinta viteza pe axa jetului), grosimea stratului limita al jetului creste proportional cu distanta (x + p) de la sectiunea de iesire a ajutajului, iar viteza scade proportional cu (x + p)^-1, (unde p reprezinta distanta intre polul jetului si sectiunea de iesire a ajutajului). Cand insa atunci grosimea jetului creste proportional cu (x+ p)^2/3, iar viteza pe axa se micsoreaza cu (x + p)^-2/3, deci jetul va fi mai ingust si vitezele vor scadea mai incet in lungul jetului, decat pentru cazul .

Domeniul de stabilitate este cuprins intre u₀₁ = 0 si u₀₁ = u_0r. Pe masura ce viteza curentului de aer insotitor creste valoarea scade, iar valoarea creste, domeniul de stabilitate ingustandu-se: in conformitate cu reprezentarea:

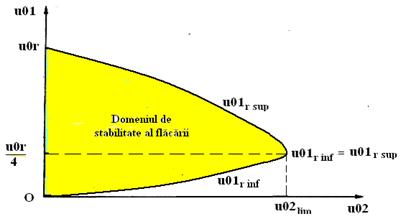
Aerul chimic necesar pentru arderea combustibilului, ca si compozitia produsilor arderii se stabilesc pe baza ecuatiei care exprima global reactiile de oxidare a combustibilului, respectandu-se principiul conservarii masei pentru fiecare dintre elementele reactantilor. Daca combustibilul este o hidrocarbura cu compozitia generata C_mH_n reactia globala de oxidare completa are forma:

in care: coeficientii stoichiometrici (1, a, b, c) sunt exprimati in moli.

Conservarea masei pentru carbon se exprima prin conditia b = m, iar pentru hidrogen prin conditia c = n/2; in fine, conservarea masei oxigenului impune conditia a = m + n/5.

Pentru verificarea relatiilor analitice, referitoare la lungimea si stabilitatea flacarilor difuziv turbulente ale combustibililor gazosi, in jeturi libere s-au efectuat cercetari experimentale pe flacari difuzive de gaz metan, in laboratorul Catedrei de Echipament termomecanic clasic si nuclear din Universitatea Politehnica Bucuresti. Pentru fiecare tip de arzator au fost efectuate masurari pentru:

- debitul de gaz metan;

- temperatura gazului metan;

- presiunea gazului metan;

- debitul de aer;

- temperatura aerului;

- presiunea aerului;

- lungimea flacarii;

- lungimea de acrosare a flacarii;

- debitul de gaz metan la care flacara s-a rupt.

Diametrul de iesire al aerului insotitor .

7.2 Contributii

Activitatea de cercetare stiintifica efectuata de autorul tezei de doctorat pentru realizarea temei: "Contributii la studiul stabilitatii flacarilor de gaze combustibile in jeturi turbulente" s-a concretizat prin urmatoarele contributii originale:

► Proiectarea si experimentarea a patru arzatoare pentru flacari axial simetrice cu posibilitatea de ardere difuziva si ardere mixta difuziv - cinetica.

► Program detaliat de efectuare a cercetarilor experimentale pentru analiza stabilitatii flacarilor axial simetrice. difuziv turbulente si difuziv-cinetice turbulente. Instalatia experimentala utilizata a permis analiza stabilitatii flacarilor axial simetrice la actiunea laterala a unui jet de aer.

► Evidentierea comparatiei intre parametrii viteza, temperatura si concentratie, in functie de diametrul canalelor duzelor.

► Modelarea numerica a flacarilor difuziv turbulente axial simetrice.

Regimul de curgere se considera turbulent, modelul de turbulenta ales fiind k-e. Fenomenul de ardere este considerat stationar.

Nu se tine cont de forta gravitationala. Caldurile specifice ale componentelor de reactie se considera variabile cu temperatura absoluta.

In urma analizei cu programul Fluent, a rezultat distributia de viteze rezultante, campul de temperaturi si concentratiile masice ale componentelor reactiei.

►Modelarea numerica cu metoda volumului finit a unei configuratii cu trei duze cu axele paralele in acelasi plan.

S-au determinat campurile de viteze, de temperaturi si de fractii masice pentru , , si .

Modelarea numerica cu metoda volumului finit a influentei unui jet lateral de aer asupra caracteristicilor unei flacari difuzive axial simetrice.

► Analiza influentei fluctuatiilor turbulentei asupra vitezei de propagare a flacarilor amestecurilor omogene combustibil - aer.

Viteza de propagare a flacarilor turbulente se exprima sub forma 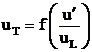, unde: reprezinta fluctuatiile, viteza in regim laminar.

Pentru si vitezele de propagare ale flacarilor laminare, notate corespunzator cu indicii 1() respectiv 2() se determina din datele experimentale prin interpolare cubica spline.

►Utilizarea metodei modelarii fractiei de amestec / PDF ( Probability Density Functions) in studiul arderii difuzive a combustibililor gazosi.

Valorilor numerice pentru si in functie de se obtin cu urmatorul algoritm:

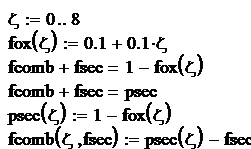
► Aplicarea ajustarii polinomiale la prelucrarea rezultatelor experimentale obtinute la arderea difuziva si difuziv - cinetica a combustibililor gazosi. Pentru flacari axial simetrice provenite din arderea in atmosfera libera, prin aplicarea metodei celor mai mici patrate, au fost obtinute polinoamele:

• ;
• ;
• ,

► Obtinerea functiilor de ajustare:

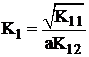- functia care determina influenta distantei x (in lungul axei jetului) asupra integralelor K₁₁ si ( si .)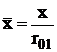

- determinarea ecuatiei de regresie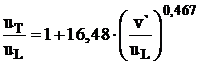

- functia de regresie polinomiala de gradul trei pentru determinarea variatiei vitezei u02 in in raport cu viteza de rupere u01r:

► Calculul limitelor de stabilitate ale flacarii intr-un cuptor rotativ, la care aerul se introduce prin intreaga sectiune a cuptorului, iar gazul combustibil (gaze naturale 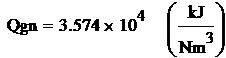se introduce la temperatura de 0 C printr-o conducta cu diametrul interior D1 = 40 mm.

Sarcina termica nominala a cuptorului:

Viteza medie a curentului de aer in cuptor:

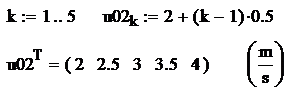
►Determinarea unghiului () de intoarcere a flacarii axial simetrice supusa actiunii unui jet de aer lateral:

,

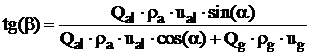unde indicele "al" se refera la aerul lateral iar "g" reprezinta gazul ; Q este debitul (), este densitatea (), u exprima viteza (), reprezinta unghiul fata de verticala a directiei vitezei aerului lateral iar este unghiul fata de verticala a directiei vitezei flacarii rezultate.

► Determinarea functiilor de interpolare ale constantelor de echilibru, in functie de temperatura, pentru substantele: H, OH, , O, N si .

Functiile de interpolare se exprima prin relatiile:

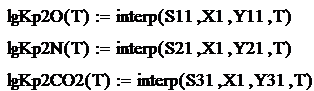
si permit calculul valorilor logaritmate ale constantelor de echilibru.

Pentru determinarea constantelor de echilibru se aplica relatiile:

► Determinarea prin analiza dimensionala a doua criterii de similitudine pentru lungimea flacarilor difuzive. Lungimile flacarilor difuzive se pot calcula cu relatiile:

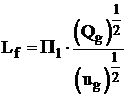, respectiv ,

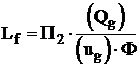unde este diametrul duzei, , respectiv .

Rezultatele obtinute in teza de doctorat sunt utile in analiza stabilitatii flacarilor difuziv turbulente axial simetrice.

In domeniul arderii difuzive a combustibililor gazosi se pot dezvolta urmatoarele cercetari:

- modelarea proceselor termogazodinamice legate de dezvoltarea flacarii unui arzator complex intr-un spatiu impus;

- dimensionarea arzatorului, partea difuziva si partea de preamestec aer-combustibil gazos, pentru diferite regimuri de functionare;

- cercetari experimentale cu determinarea caracteristicilor termogazodinamice ale flacarii si a emisiilor poluante de NOx si CO;

- realizarea unor flacari difuzive cu anumite caracteristici care sa satisfaca cerintele diferitelor procese tehnologice, pe baza cunoasterii factorilor fizici, chimici si geometrici care influenteaza asupra caracteristicilor flacarilor combustibililor gazosi;

BIBLIOGRAFIE