Transformari ale numarului de faze

Transformari ale numarului de faze

In paragrafele anterioare s-a analizat expresia tensiunii magnetice, produsa in intrefierul unei masini asincrone de catre o infasurare m-fazata.

In cazurile practice se utilizeaza infasurari monofazate, bifazate, trifazate si infasurari in colivie. Infasurarea in colivie este o infasurare -fazata, unde este numarul de bare al coliviei.

In unele cazuri practice prezinta interes echivalarea unei infasurari printr-o alta infasurare avand un numar diferit de faze.

Transformarea numarului de faze conduce si la transformari de variabila pentru ca infasurarile echivalente obtinute sunt parcurse de alti curenti decat infasurarile date si au alte tensiuni la borne.

Se considera ca o infasurare este simetrica daca infasurarile de faza sunt dispuse echidistant la periferia armaturii. O infasurare echilibrata are acelasi numar de spire pe fiecare faza.

1. Echivalarea unei infasurari prin infasurari polifazate

simetrice si echilibrate

Echivalarea unei infasurari cu ajutorul unor infasurari polifazate simetrice si echilibrate, alimentate prin sisteme simetrice si echilibrate de curenti se face prin conservarea expresiei tensiunii magnetice din intrefier. In ambele cazuri armonica spatiala de ordin j a tensiunii magnetice rezultante se obtine prin insumarea armonicilor spatiale, de acelasi ordin, produse de fiecare faza in parte.

a.      Echivalarea unei infasurari monofazate

Se considera o infasurare monofazata dispusa la periferia unei armaturi cilindrice si parcursa de curentul i:

Pentru generalizare vom considera ca axa magnetica a infasurarii este decalata inainte, fata de axa de referinta a armaturii cu unghiul - vezi figura 2.19.a. Infasurarea are spire si determina in intrefier un camp magnetic avand p perechi de poli.

Conform (2.20.b) tensiunea magnetica, de armonica spatiala j, determinata de infasurarea considerata, are expresia:

(2.38)

unde amplitudinea se determina cu relatia (2.20.a), iar reprezinta numarul de spire echivalent pentru armonica spatiala j (2.18.b).

Transformand produsul de functii trigonometrice in suma, expresia tensiunii magnetice de armonica spatiala j devine

unde s-au efectuat notatiile:

unda magnetica de succesiune directa

(2.38.a)

unda magnetica de succesiune inversa

(2.38.b)

Cele doua infasurari m-fazate sinusoidale se considera identice ca structura si au urmatoarele caracteristici:

fiecare infasurare sinusoidala de faza are spire echivalente pe faza pentru armonica j

numarul de spire echivalente pe faza se determina din conditia conservarii amplitudinii undei progresive (vezi egalitatea (2.38) si (2.25.a)):

(2.39)

unde s-a notat cu valoarea efectiva a sistemului de curenti care alimenteaza infasurarea polifazata.

In ipoteza pastrarii valorii efective a curentului, din egalitatea (2.39) rezulta:

(2.39.a)

infasurarile sunt executate din conductoare filiforme, dispuse sinusoidal pe periferia armaturii, astfel incat fiecare infasurare produce numai o singura unda a tensiunii magnetice

Fazele celor doua infasurari trifazate sinusoidale au asezari diferite:

fazele infasurarii care determina unda de succesiune directa se succed, spatial, la periferia armaturii in sens crescator coordonatei spatiale;

fazele infasurarii care determina unda de succesiune inversa se succed, spatial, la periferia armaturii in sens descrescator coordonatei spatiale;

Fazele de acelasi nume ale celor doua infasurari sunt inseriate, infasurarile fiind alimentate cu un sistem simetric si echilibrat de curenti de succesiune directa - vezi sistemul (2.23.a)

(2.39.c)

iar curentul care parcurge infasurarea de referinta (faza 1) este chiar curentul care parcurge infasurarea monofazata data. Cele doua infasurari trifazate inseriate sunt conectate in stea.

In figura 2.19 este prezentata echivalarea unei infasurari sinusoidale monofazate cu doua infasurari trifazate sinusoidale.

b. Echivalarea unei infasurari bifazate

Vom considera cazul general al unei infasurari bifazate oarecare care determina p perechi de poli magnetici. Infasurarile de faza au numere diferite de spire si repartitii diferite, iar intre axele lor spatiale este un decalaj spatial . Infasurarea fazei 2 se considera decalata spatial inainte fata de infasurarea fazei 1, care are axa magnetica suprapusa peste axa spatiala de referinta a armaturii - vezi figura 2.20.a.

In cazul in care infasurarile sunt parcurse de un sistem bifazat, oarecare, de curenti:

tensiunea magnetica rezultanta , de armonica spatiala j, are expresia (vezi relatiile (2.20) si (2.20.b))

(2.40)

unde amplitudinile si au expresiile

(2.40.a)

S-au notat cu si numerele de spire echivalente pentru armonica spatiala j (vezi (2.18.b)) a celor doua infasurari.

Expresia (2.40) a tensiunii magnetice de armonica spatiala j se poate scrie, dupa unele prelucrari trigonometrice, sub forma:

in care cele doua componente, denumite componente de succesiune directa si respectiv de succesiune inversa, au expresiile:

componenta de succesiune directa :

(2.41.a)

componenta de succesiune inversa :

(2.41.b)

Amplitudinile si au expresiile precizate de relatiile (2.40.a).

Cele doua infasurari m-fazate sinusoidale se considera identice ca structura si au urmatoarele caracteristici:

fazele se succed la periferia armaturii in sensul crescator al coordonatei spatiale;

fiecare infasurare are spire echivalente, corespunzand numarului mediu de spire a celor doua infasurari date:

(2.42)

axa magnetica a fazei de referinta (faza 1) se suprapune peste axa de referinta spatiala, ca si axa magnetica a fazei de referinta a infasurarii bifazate

infasurarea care determina unda de succesiune directa este parcursa de un sistem simetric si echilibrat de curenti de succesiune directa:

(2.43)

unde defazajul se determina cu relatia (2.41.a), iar valoarea efectiva a se obtine din conditia conservarii amplitudinii a undei (2.41.a):

respectiv (2.43.a)

infasurarea care determina unda de succesiune inversa este parcursa de un sistem simetric si echilibrat de curenti de succesiune inversa:

(2.44)

unde defazajul se determina cu relatia (2.41.b), iar valoarea efectiva a fost obtinuta din conditia conservarii amplitudinii a undei (vezi 2.41.b):

respectiv (2.44.a)

infasurarile de faza sunt executate din conductoare filiforme, dispuse sinusoidal pe periferia armaturii, astfel incat fiecare produce numai o singura unda a tensiunii magnetice

numarul m de faze este corelat cu ordinul j al armonicilor spatiale prin conditia (2.38.c):

In figura 2.20 este prezentata echivalarea unei infasurari bifazate cu doua infasurari trifazate.

Observatie

Cazul particular al unei infasurari bifazate simetrice (infasurarile au acelasi numar de spire echivalente si sunt decalate spatial cu unghiul se obtine prin considerarea valorilor particulare

si

c. Echivalarea unei infasurari polifazate, simetrice si dezechilibrate,

alimentata cu un sistem polifazat simetric si dezechilibrat de curenti

Consideram cazul unei infasurari n-fazate simetrice (infasurarile sunt dispuse echidistant la periferia armaturii) si dezechilibrata (cu numere diferite de spire pe faze) parcursa de un sistem simetric si dezechilibrat, de curenti:

Tensiunea magnetica rezultanta din intrefier pentru armonica spatiala j, obtinuta prin insumarea tensiunilor magnetice produse de fiecare infasurare de faza (vezi relatiile (2.20) si (2.20.b) va avea expresia:

(2.45)

unde

(2.45.a)

reprezentand numarul echivalent de spire, pentru armonica j a infasurarii de faza .

Cele doua infasurari m-fazate sinusoidale se considera identice ca structura si asezare si au urmatoarele caracteristici:

fazele se succed la periferia armaturii in sensul crescator al coordonatei spatiale;

fiecare infasurare de faza sinusoidala are spire echivalente, corespunzand numarului mediu de spire pe faza ale celor n infasurari date

(2.45.b)

axa magnetica a fazei de referinta (faza 1) se suprapune peste axa de referinta spatiala, ca si axa magnetica a fazei de referinta a infasurarii n-fazate considerate

infasurarea care determina unda de succesiune directa este parcursa de un sistem simetric si echilibrat de curenti de succesiune directa:

(2.45.c)

unde defazajul se calculeaza cu relatia (2.45.a), iar valoarea efectiva se obtine din conditia conservarii amplitudinii (2.45.a) a undei si are expresia (2.43.a):

infasurarea care determina unda de succesiune inversa este parcursa de un sistem simetric si echilibrat de curenti de succesiune inversa:

(2.45.d)

unde defazajul se calculeaza cu relatia (2.45.a), iar valoarea efectiva se obtine din conditia conservarii amplitudinii (2.45.a) a undei si are expresia (2.44.a):

infasurarile sunt executate din conductoare filiforme dispuse sinusoidal pe periferia armaturii, astfel incat fiecare produce numai o singura a tensiunii magnetice

numarul m de faze este corelat cu ordinul j al armonicii spatiale prin conditia (2.38.c)

In figura 2.21 este prezentata echivalarea unei infasurari n-fazate cu doua infasurari trifazate.

Observatie

Echivalarea unei infasurari n-fazate simetrice si echilibrate, alimentata cu un sistem simetric si echilibrat de curenti, printr-o infasurare m-fazata alimentata cu un sistem simetric si echilibrat de curenti de curenti poate fi tratata ca un caz particular in care:

toate fazele au acelasi numar de spire

valorile efective ale curentilor de faza sunt aceleasi

In acest caz armonica spatiala de ordin j a tensiunii magnetice rezultante are numai una din componente:

sau

unde

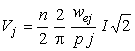
Infasurarea n-fazata va fi echivalata printr-o singura infasurare m-fazata parcursa de sistemul de curenti (2.45.c) de succesiune directa pentru cazul in care se produce numai armonica spatiala de succesiune directa sau de sistemul de curenti (2.45.d) de succesiune inversa in cazul in care se produce unda inversa .

Cele doua sisteme de curenti au aceeasi valoare efectiva :

egala cu valoarea efectiva a curentilor care parcurg infasurarea data. Aceasta valoare rezulta din conditia de conservare a amplitudinii a tensiunii magnetice de armonica spatiala j, daca numarul de spire pe faza a infasurarii m-fazate se calculeaza cu relatia (2.45.b):

d. Echivalarea unei infasurari polifazate simetrice alimentata cu un sistem polifazat oarecare de curenti

Consideram cazul unei infasurari n-fazate, simetrica si dezechilibrata, care este parcursa de un sistem dezechilibrat si nesimetric de curenti:

(2.46)

Daca se accepta descompunerea trigonometrica a expresiei unui curent de pe o faza oarecare:

atunci se poate considera ca sistemul de curenti (2.46) se descompune in doua sisteme simetrice si dezechilibrate de curenti:

sistemul a:

(2.46.a)

sistemul b:

(2.46.b)

Cele doua sisteme echivalente de curenti au acelasi numar de faze si aceeasi succesiune a fazelor ca si sistemul real de curenti. Curentii de faza ai celor doua sisteme echivalente sunt defazati unul fata de altul cu radiani (sunt in cuadratura).

2. Echivalarea unei infasurari prin infasurari bifazate

Dintre infasurarile polifazate, infasurarea bifazata, simetrica avand un decalaj spatial de intre faze (p este numarul de perechi de poli magnetici determinati de infasurare) are avantajul decuplarii magnetice a infasurarilor (campul magnetic produs de curentul dintr-o faza nu induce tensiuni electromotoare in cealalta faza).

a)      Echivalarea unei infasurari monofazate printr-un sistem bifazat simetric de infasurari

Consideram o infasurare monofazata realizata cu conductoare filiforme, dispuse la periferia armaturii fixe a unei masini, cu intrefierul de largime constanta _e. Axa magnetica a infasurarii este decalata cu unghiul in raport cu axa spatiala de referinta a armaturii, in sensul pozitiv al coordonatei spatiale (figura 2.22.a).

Infasurarea monofazata determina in intrefier o tensiune magnetica, cu p perechi de poli. Armonica spatiala de ordin j a acestei tensiuni magnetice are expresia (2.20.b):

(2.47)

cu amplitudinea:

, (2.47.a)

unde este numarul de spire echivalent pentru armonica j (2.18.b), iar curentul electric care o parcurge are expresia:

(2.47.b)

Daca in argumentul functiei spatiale din egalitatea (2.47) adunam si scadem unghiul si dezvoltam trigonometric aceasta functie, dupa ordonare, se obtine:

(2.48)

Relatia (2.48) este echivalenta relatiei (2.47) si arata ca infasurarea monofazata sinusoidala care produce armonica spatiala de ordin j a tensiunii magnetice poate fi inlocuita, din punct de vedere al tensiunii magnetice, printr-o infasurare bifazata sinusoidala cu urmatoarele proprietati:

axa magnetica a infasurarii longitudinale, care determina tensiunea magnetica , este rotita cu unghiul in urma axei magnetice a infasurarii date; aceasta axa magnetica se mai numeste si axa longitudinala - axa l

axa magnetica a infasurarii transversale, care determina tensiunea magnetica , este rotita inainte cu unghiul in raport cu axa magnetica a infasurarii longitudinale; aceasta axa magnetica se mai numeste si axa transversala - axa t

cele doua infasurari sunt identice cu infasurarea data si au acelasi numar de spire echivalent :

amplitudinea curentilor care strabat infasurarile bifazate depind de pozitia aleasa pentru axa longitudinala l si de ordinul j al armonicii tensiunii magnetice (vezi figura 2.22.b):

(2.49)

unde curentul i, care parcurge infasurarea data, are expresia (2.47.b).

Relatia (2.49) sugereaza o schimbare de variabila, inlocuind variabila i cu variabilele si ; aceasta schimbare de variabila este reprezentata matriceal prin relatia:

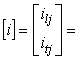
, (2.49.a)

unde matricea de transformare a curentilor are expresia:

= . (2.49.b)

Adoptam pentru tensiuni aceeasi matrice de transformare :

,

unde u este tensiunea la bornele infasurarii monofazate sinusoidale considerate. In aceste conditii expresia puterii instantanee pentru infasurarea bifazata echivalenta este:

. (2.49.c)

Relatia (2.49.c) confirma faptul ca transformarea , definita de relatia (2.49.b) conserva expresia puterii instantanee la bornele circuitelor.

b) Echivalarea unei infasurari bifazate printr-o alta infasurare bifazata

Consideram un sistem bifazat format din doua infasurari monofazate a si b, decalate spatial cu unghiul ( vezi figura 2.23.a).

Infasurarile, considerate identice din punct de vedere constructiv, sunt parcurse de curentii sinusoidali si . Fiecare infasurare are spire echivalente pentru armonica spatiala j a tensiunii magnetice din intrefier.

Folosind transformarea (vezi relatia (2.49.b)), vom echivala fiecare din cele doua infasurari date cu un sistem bifazat de infasurari a carui faza de referinta l are axa magnetica decalata spatial in urma fazei a cu unghiul (vezi figura 2.21.a). Daca echivalarea se efectueaza in raport cu armonica de ordin j a tensiunii magnetice din intrefier, atunci se obtine:

respectiv

[i_ab] , (2.50)

Fig.2.23. Explicativa privind echivalarea unei infasurari bifazate printr-o infasurare bifazata rectangulara

a)       echivalarea unei infasurari bifazate oarecare printr-o infasurare bifazata simetrica;

b)       echivalarea unei infasurari bifazate simetrice printr-o alta infasurare bifazata simetrica

c)       echivalarea unei infasurari bifazate simetrice, fixe, printr-o infasurare bifazata mobila

unde matricea de transformare este nesingulara si are expresia:

= , (2.50.a)

iar si sunt curentii care parcurg infasurarile echivalente.

Daca pentru tensiuni se adopta aceeasi schimbare de variabila (2.50.a) rezulta:

(2.50.b)

Puterea instantanee primita pe la bornele sistemului bifazat echivalent de infasurari este

,

expresie care, in cazul considerarii relatiilor (2.50) si (2.50.b) devine

,

unde matricile care au indicele t sunt matrici transpuse.

Se constata ca transformarea nu conserva expresia puterii instantanee la borne, deoarece matricea transformarii nu este o matrice ortogonala.

Pentru ca matricea (2.40.a) a transformarii sa fie ortogonala, trebuie sa fie satisfacuta egalitatea:

= , respectiv: =[1] ,

rezultand conditia:

, respectiv: . (2.50.c)

Daca infasurarile sistemului bifazat dat satisfac conditia (2.50.c), adica sunt simetrice atunci matricea transformarii devine:

= (2.50.d)

In cazul in care noul sistem bifazat se roteste, in raport cu vechiul sistem bifazat, in sensul pozitiv al coordonatei spatiale (vezi figura 2.23.c), matricea transformarii va avea expresia:

= , (2.51)

unde este unghiul de pozitie a sistemului mobil la un moment dat. In cazul efectuarii unei rotatii cu viteza unghiulara constanta , unghiul de pozitie are expresia

,

iar este decalajul initial intre axele l si a - vezi figura 2.23.c; transformarea (2.51) se obtine din transformarea (2.50.d), considerand .

Relatia (2.51) permite echivalarea unui sistem bifazat fix de infasurari intr-un sistem bifazat mobil de infasurari.

c) Echivalarea unei infasurari trifazate alimentata cu un sistem trifazat simetric si echilibrat de curenti, printr-o infasurare bifazata

Asa cum s-a prezentat in paragraful 2.2.1.3., relatiile (2.25.a) sau (2.25.b), orice infasurare polifazata, alimentata cu un sistem polifazat simetric si echilibrat de curenti poate fi echivalata, din punct de vedere al armonicii spatiale de ordin j, printr-o infasurare bifazata.

Proprietatea importanta a infasurarilor polifazate simetrice alimentate cu un sistem polifazat simetric si echilibrat de curenti consta in faptul ca tensiunea magnetica rezultanta din intrefier are numai anumite armonici spatiale nenule, indiferent de valoarea coeficientului de infasurare , respectiv al numarului echivalent de spire.

Pentru cazul particular al infasurarii trifazate, expresia armonicii spatiale de ordin j a tensiunii magnetice rezultante este:

a. pentru ordinul (vezi (2.25.a)):

(2.52.a)

b. pentru ordinul (vezi (2.25.b)):

(2.52.b)

c. pentru ordinul , (vezi (2.24.c)):

unde amplitudinea are expresia (2.25.c)

(2.52.c)

S-a considerat ca infasurarea trifazata are axa magnetica a fazei de referinta (faza 1) decalata inainte cu unghiul fata de axa de referinta spatiala a armaturii (vezi figura 2.24.a), coordonata spatiala fiind notata cu , iar sistemul trifazat de curenti care alimenteaza infasurarea este un sistem simetric si echilibrat de curenti, de succesiune directa:

(2.52.d)

Fig. 2.24. Transformarea unei infasurari trifazate sinusoidale intr-o

infasurare bifazata sinusoidala

a)       asezarea spatiala, pe stator, a infasurarii trifazate sinusoidale;

b)       asezarea spatiala, pe stator, a infasurarii bifazate sinusoidale echivalente;

c) asezarea spatiala, pe rotor, a infasurarii bifazate sinusoidale echivalente

c1) Cazul particular al armonicilor spatiale de ordin

Analiza expresiei (2.52.a) arata ca tensiunea magnetica de armonica spatiala poate fi considerata ca produsa de o infasurare bifazata (vezi figura 2.24.b) cu urmatoarele proprietati:

una din infasurarile monofazate, numita infasurare longitudinala, are axa magnetica suprapusa peste axa de referinta spatiala a armaturii - vezi factorul spatial din primul termen al expresiei (2.52.a);

a doua infasurare monofazata, numita infasurare transversala are axa magnetica decalata inainte cu unghiul in raport cu axa infasurarii longitudinale - vezi factorul spatial din al doilea termen al expresiei (2.52.a);

cele doua infasurari sunt identice, avand fiecare spire echivalente;

infasurarea longitudinala este parcursa de curentul:

(2.53.a)

(vezi factorul temporal din primul termen al expresiei (2.52.a));

infasurarea transversala este parcursa de curentul:

(2.53.b)

defazat cu fata de curentul (2.45.a) (vezi factorul temporal din al doilea termen al expresiei (2.52.a);

curentii si parcurg infasurarile in sensul pozitiv al curentului prin infasurarea fazei de referinta a infasurarii m-fazate si au aceeasi pulsatie cu acesta.

Din compararea relatiei (2.52.c) cu relatia (2.17.a), care exprima amplitudinea tensiunii magnetice determinata de o infasurare monofazata, rezulta trei posibilitati de echivalare a numarului de spire echivalent pe faza si a valorii efective a curentului de faza din infasurarea bifazata:

varianta A: 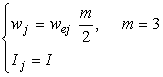(2.54.a)

unde este numarul de spre echivalente pe faza al infasurarii trifazate, I este valoarea efectiva a curentilor din sistemul trifazat (vezi 2.52.d), iar m este numarul de faze.

varianta B: (2.54.b)

varianta C: (2.54.c)

Relatia de transformare a sistemului (2.52.d) al curentilor care alimenteaza infasurarea trifazata in sistemul curentilor care alimenteaza infasurarea bifazata, folosind (2.54.a) si (2.54.b) se poate scrie matricial in forma:

(2.55)

unde constanta are valori diferite in raport cu varianta de echivalare folosita pentru numerele de spire si pentru valorile efective ale curentilor (vezi (2.54.a), (2.54.b), (2.54.c)

varianta A

varianta B (2.55.a)

varianta C

Relatiile prezentate anterior corespund cazului in care infasurarea bifazata se gaseste pe aceeasi armatura cu infasurarea m-fazata pe care o echivaleaza.

Se poate face si o echivalare in care infasurarea m-fazata se gaseste pe o armatura (de exemplu pe stator - vezi figura 2.24.a), iar infasurarea bifazata pe cealalta armatura (de exemplu pe rotor - vezi figura 2.24.c). Daca rotorul se deplaseaza in sensul crescator al coordonatei spatiale, atunci intre coordonatele spatiale din stator si din rotor exista relatia (vezi figura 2.24.c):

unde reprezinta defazajul dintre axele de referinta spatiala din stator si rotor, la momentul t.

In acest caz, expresiile curentilor care strabat infasurarile longitudinala si transversala sunt:

(2.46.a)

cu

Ca urmare relatia de transformare a curentilor poate fi scrisa matricial sub forma:

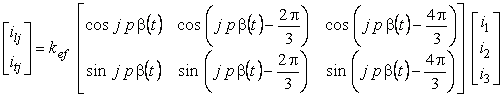(2.56.b)

Matricile de transformare din relatiile (2.55), respectiv (2.56.b) nu sunt utilizabile pentru transformarea unui sistem de ecuatii de tensiune pentru ca nu sunt matrici patrate, si deci nu sunt inversabile. Pentru a elimina acest inconvenient se introduce o noua variabila de curent definita prin relatia:

(2.57)

iar matricea de transformare se poate completa cu o noua linie devenind o matrice patrata.

Valorile si se determina in functie de variabilele :

(2.58)

unde matricea de transformare are expresia:

pentru cazul in care infasurarea bifazata se gaseste pe aceeasi armatura cu infasurarea trifazata (vezi figura 2.24.b):

(2.58.a)

pentru cazul in care infasurarea bifazata se gaseste pe alta armatura decat infasurarea trifazata (vezi figura 2.24.c):

(2.58.b)

Constantele si depind de varianta de echivalare folosita:

constanta este precizata de relatia (2.55.a)

constanta are valorile:

varianta A

varianta B    (2.58.c)

varianta C

Indiferent de varianta de echivalare utilizata, matricea de transformare este nesingulara astfel ca sistemul de curenti definit de relatia (2.58) rezulta univoc daca se cunoaste sistemul de curenti . Fiind nesingulara, matricea este inversabila, astfel incat aceasta transformare poate fi utilizata si pentru transformarea unor ecuatii de tensiune.

c2) Cazul particular, al armonicilor spatiale de ordin

Consideram o infasurare trifazata (vezi figura 2.24.a) alimentata cu un sistem trifazat simetric si echilibrat de curenti (2.52.d). Analiza expresiei (2.52.b) arata ca armonica spatiala a tensiunii magnetice de ordin , se poate considera ca este produsa de o infasurare bifazata (vezi figura 2.24.b) cu urmatoarele proprietati:

una din infasurarile monofazate, numita infasurare longitudinala are axa magnetica suprapusa peste axa spatiala a armaturii si este parcursa de curentul:

(2.59.a)

a doua infasurare monofazata, numita infasurare transversala, are axa magnetica decalata inainte cu unghiul:

fata de axa magnetica a infasurarii longitudinale. Infasurarea transversala este parcursa de curentul:

(2.59.b)

defazat cu inaintea curentului .

din relatia (2.52.c) rezulta ca cele doua infasurari monofazate sunt identice, avand fiecare spire echivalente;

curentii si parcurg infasurarile in sensul pozitiv al curentului prin faza de referinta a infasurarii m-fazate si are aceeasi pulsatie cu acesta;

exista trei posibilitati de definire a numarului de spire echivalente si a valorii efective a curentului - vezi relatiile (2.54.a), (2.54.b) si (2.54.c).

Relatia de transformare a sistemului curentilor care parcurg infasurarea trifazata (vezi relatia (2.52.d), in sistemul curentilor care parcurg infasurarea bifazata, folosind (2.59.a) si (2.59.b) este:

(2.59.c)

Transformarea (2.59.c) corespunde cazului in care infasurarea bifazata este asezata pe aceeasi armatura cu infasurarea trifazata (in cazul considerat pe stator), iar curentii infasurarii trifazate satisfac conditia .

Infasurarea bifazata asezata pe rotor (vezi figura 2.24.c), echivalenta infasurarii trifazate asezata pe stator (vezi figura 2.24.a), are proprietatile enumerate anterior si este parcursa de curentii