Codificarea informatiei in calculatoarele numerice

Codificarea informatiei in calculatoarele numerice

I.1.1 Despre coduri si codificare

Codul este o modalitate de reprezentare simbolica, a elementelor unei multimi. Un cod va realiza practic o corespondenta biunivoca intre doua multimi si anume:

Ø      O colectie* de obiecte, care este formata din elementele unei multimi care au un set de caracteristici de acelasi tip. Aceasta este multimea care se codifica.

Ø      O multime, in general structurata, de simboluri. Aceasta este multimea codurilor.

Nota: * Termenul de colectie de obiecte va fi explicat ulterior.

Exemplu.      Coduri intalnite foarte des:

Codificarea, este metoda prin care se acorda coduri (simboluri) elementelor unei colectii de obiecte.

Exista diferite tipuri de metode de codificare, dar ele trebuie sa asigure in primul rand unicitatea codului. Cele mai utilizate sunt:

Cea mai simpla metoda de codificare este codificarea secventiala, prin care se acorda in ordine numere multimii de codificat. De exemplu numarul matricol acordat elevilor dintr-o unitate de invatamant este un astfel de cod. Avantajul este simplitatea, numarul mic de pozitii ocupate, dar dezavantajul este ca acesta nu transmite nici o informatie adiacenta.

O alta modalitate este codificarea secventiala, pe intervale. De exemplu putem forma un cod pentru studentii unei facultati astfel Codurile de la 1-10,000 sunt date in ordine studentilor de la sectia A, cele intre 10,001-20,000, celor de la sectia B, etc. Dezavantajul este greutatea in folosire fiind destul de complicat.

O metoda foarte utilizata este codificarea structurata pe grupe, in care codul se formeaza din mai multe grupe de caractere, fiecare dintre acestea reprezentand un anumit lucru, de asemenea codificat. Avantajul este ca un asemenea cod transmite multe informatii adiacente, iar dezavantajul este ca ocupa destul de multe pozitii, fiind usor de gresit. Din aceasta cauza se obisnuieste atasarea la acest cod a unei cifre de control

De exemplu CNP (Codul numeric personal), este un cod numeric structurat, din 13 caractere, format din mai multe grupe, care reprezenta ele insele alte coduri. El are urmatoarea structura

La randul sau, caracterul 1 (Sexul si secolul), este codificat secvential pe intervale si anume:

à          Codurile 1 si 2 reprezinta sexul M respectiv F, secolul 20 (adica 1900

à          Codurile 3 si 4 reprezinta sexul M respectiv F, secolul 19 (adica 1800

à          Codurile 5 si 6 reprezinta sexul M respectiv F, secolul 21 (adica 2000

Observatia 1. Acest cod, pe langa functia lui de baza, de identificare a unei persoane, transmite si alte doua lucruri foarte importante sexul si data nasterii.

Observatia 2. Cu toate ca se tot spune ca inceputul noul secolului este anul 2001, si din practica curenta se observa ca lucrurile nu stau de loc asa.

Explicatie. Cifra de control (CC) este o informatie redundanta, care permite un control al exactitatii codului.

De exemplu o modalitate de calcul a cifrei de control pentru un cod format din cifre zecimale este modulo 10 din suma cifrelor din cod. Astfel daca avem un cod acestuia i se va adauga o CC ) Mod (10) Deci intregul cod este acum 37224. Presupunem ca vom folosi acum acest cod dar el va ajunge eronat, 36224. Acum se calculeaza din nou CC, si daca aceasta nu este egala cu cea din cod, vom stii ca avem un cod eronat. CC ) Mod(10) Deci CC calculata, , fiind diferita de CC din codul primit, adica vom stii precis ca acest cod este eronat.

I.1.2 Calculatoare numerice si analogice

Am aratat ca obiectul de studiu al informaticii, il constituie gestiunea informatiei cu ajutorul calculatorului. Pentru aceasta, bineinteles primul lucru care trebuie facut este ca informatia sa poata fi memorata' de calculator, deci trebuie codificata, cu o metoda care sa conduca la un cod acceptat de structura acestuia.

Nota: Notiunea de data se refera la informatia preluata in calculator.

Din acest punct de vedere exista doua tipuri principale de calculatoare, analogice si numerice.

Calculatoarele analogice au ca principiu de functionare reprezentarea datelor printr-o marime fizica, analogica, continua. De exemplu presupunem ca numerele sunt reprezentate de valoarea unei tensiuni; astfel numarul 3 va fi reprezentat de tensiunea de 3V, numarul 8.22 de tensiunea de 8.22V, etc. Adunarea numerelor se va face printr-un dispozitiv de insumare a tensiunilor. Deci un astfel de sistem, necesita o codificare a informatiei in marimea fizica respectiva. Acest tip de calculatoare, care au avantajul unei precizii si viteze mari in executie, au fost folosite in aplicatii de proces - programe care au ca interfata cu exteriorul un proces tehnologic, datele de intrare provenind de la acesta, iar rezultatele intorcandu-se in proces pentru a actiona asupra unor parametrii ai acestuia. Acest sistem era adecvat, deoarece codificarea informatiei, pentru a putea fi introdusa in calculator se facea prin niste traductori ai unor parametrii(de exemplu transformarea temperaturii in intensitate a curentului electric),  iar rezultatele, erau decodificate, tot la nivelul unei marimi fizice care actiona un dispozitiv de reglare a unui parametru (de exemplu rezultatul putea fi producerea unei tensiuni, pe o anumita durata, care sa actioneze direct o valva de la o conducta de aburi, prin care se regla ca temperatura procesului sa respecte o anumita traiectorie), sau era pur si simplu afisat.

Desi calculatoarele analogice erau performante din toate punctele de vedere, ele aveau un mare dezavantaj - care de altfel a dus la incetarea producerii lor - si anume, aria mica de utilizare. Practic aceste calculatoare erau concepute pentru o anumita aplicatie specifica. Acest lucru, evident, a dus la costuri foarte mari si la sume mici de fonduri destinate cercetarii si dezvoltarii.

Calculatoarele numerice, s-au impus in special datorita caracterului universal al folosirii lor, de la probleme de calcul matematic, la probleme de gestiune sau proces, iar o data cu aparitia microprocesoarelor, practic in toate domeniile activitatii umane.

Principala caracteristica a calculatorului numeric este ca informatia, ori care ar fi natura ei, se memoreaza si prelucreaza sub forma unor numere in sistemul binar (sistemul de numeratie in baza 2, adica format din cifrele 0 si 1). Lucrul acesta este determinat de faptul ca, din punct de vedere constructiv, calculatoarele numerice au memoria formata din niste celule care pot memora o informatie binara (un bit), deci o stare din doua posibile. Memoria acestor calculatoare, putem sa ne-o imaginam, ca pe o multime de mii de miliarde de intrerupatoare, fiecare din acestea avand doua pozitii, deci permitand memorarea unui bit.

Codificarea informatiei, in calculatoarele numerice, se va face intotdeauna in sistem binar. In general exista urmatoarele categorii de informatie ce trebuie folosita, deci codificata

Numerele intregi

Numerele reale

Caracterele, adica litere, cifre, semne speciale sau alte simboluri

Valorile Booleene, adica True (adevarat) si False (fals).

Instructiunile calculatorului. Practic acestea sunt niste numere intregi.

In continuare vom arata modalitatile prin care se realizeaza acest lucru.

I.1.3 Codificarea numerelor.

Codificarea numerelor intregi si reale se face in sistemul binar(sistemul de numeratie in baza 2, adica format din cifrele 0 si 1).

I.1.3.1 Transformarea numerelor dintr-o baza in alta.

Pentru introducerea numerelor in calculator in primul rand trebuie efectuata conversia numerelor intregi sau reale din sistemul zecimal in sistemul binar.

I.1.3.1.1 Numere intregi.

Conversia numerelor intregi din baza 10 in baza b se realizeaza prin impartiri succesive cu baza ; daca x este un numar intreg in baza 10 atunci, conform teoremei impartirii cu rest putem scrie:

x=b*q₀+r₀ , x>q₀

q₀=b* q₁+ r_{1 ,} q₀> q₁

q_n-1=b* q_n+ r_n , q_n-1> q_n

Deci (x)_b=r_nr_n-1r_n-2r₁r₀

Conversia unui numar intreg din baza b in baza 10 se realizeaza prin inmultirea fiecarei cifre a numarului cu baza la puterea pozitiei cifrei in numar:

Daca: (x)_b=x_nx_n-1x_n-2x₁x₀ atunci, (x)₁₀=x_nbⁿ+x_n-1b^n-1+..+x₁b+x₀

Exemplu.     

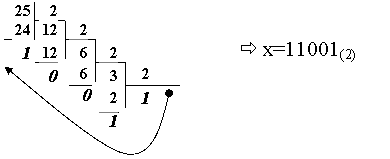
Consideram numarul intreg x=25 in baza 10. In baza 2 numarul x va avea reprezentarea:

Conversia inversa din baza 2 in baza 10 este de forma:

x=11001₍₂₎=1*2⁴+1*2³+0*2²+0*2¹+1*2⁰ = 16+8+1=25

I.1.3.1.2 Numere reale.

Un numar real X se poate scrie ca suma dintre partea intreaga si partea fractionara:

X = [x]+

Conversia unui numar real din baza 10 in baza b se face separat pentru partea intreaga si pentru partea fractionara. Conversia partii intregi se realizeaza prin impartiri succesive cu baza(analog conversiei numerelor intregi), iar conversia partii fractionare se face prin inmultiri repetate cu baza de forma:

b* = x₁=[ x₁]+=r_-1+

b*= x₂=[ x₂]+= r_-2+

b*= x_n =[ x_n]+= r_-n+

_(b)=r_-1r_-2.r_-n

Intalnim urmatoarele situatii:

Daca atunci _(b)=r_-1r_-2.r_-n

Daca ¹ atunci se poate observa o periodicitate sau se reprezinta aproximativ pastrand primele n cifre.

Un numar real x= a_na_n-1an_-2.a₀,a_-1a_-2.a_-m in baza b se poate scrie in baza 10 de forma:

x=a_nbⁿ+a_n-1b^n-1+.a₀b⁰+a_-1b^-1+..a_-mb^-m

Sistemul de numeratie hexazecimal.

Cifrele bazei 16 (sistem hexazecimal) sunt 0,1,2,.15, fiecare cifra putand fi reprezentata pe 4 biti Pentru numerele mai mari de 9 se tine cont de conventia de notare: A=10, B=11, C=12, D=13, E=14, F=15.

In general pentru usurarea si claritatea operatiilor cand se doreste conversia din baza 10 in baza 2, se va face la inceput conversia din baza 10 in baza 16, deoarece exprimarea in aceasta baza are mai putine cifre, iar dupa aceea se efectueaza conversia din baza 16 in baza 2, care este evidenta deoarece

Acest procedeu il vom folosi in continuare in urmatorul exemplu:

Exemplu.      Dorim transformarea numarului in baza 2.

La inceput vom converti numarul in baza , pe rand partea intreaga si partea fractionara.

x

=1C₍₁₆₎

0 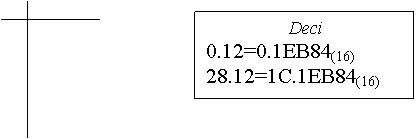12*16

1 92*16

72*16

52*16

8 32*16

4 12 (se observa periodicitatea

Dupa ce s-a obtinut numarul in baza 16, conversia in baza 2 se face usor, transfomand fiecare cifra hexazecimala , in 4 cifre binare, ca mai jos

I.1.3.2 Codificarea numerelor in calculator

I.1.3.2.1 Numere intregi.

Reprezentarea numerelor intregi in memorie depinde de numarul de biti alocati.

Astfel pentru 4 octeti 4 octeti=32biti), numarul maxim de cifre ale reprezentarii va fi <2³²-1. Numerele intregi pozitive vor fi reprezentate in intervalul iar numerele intregi negative in intervalul

De exemplu numarul x=25 va fi reprezentat pe octet(8 biti) astfel:

Celulele libere se completeaza cu cifre nesemnificative, adica 0. Primul bit se numeste bitul de semn si poate avea valoarea 0 in cazul in care numarul este pozitiv si valoarea 1 in cazul in care numarul este negativ.

Pentru reprezentarea unui numar intreg negativ se foloseste codul complementar. Trecerea unui numar in cod complementar se realizeaza schimband cifrele 0 cu 1 si 1 cu 0 dupa care se aduna 1

Astfel numarul x = -25 va avea reprezentarea:

Daca

Atunci

Pentru adunarea numerelor in sistemul binar se tine cont de regulile: 0+0=0; 0+1=1; 1+0=1; 1+1=10.

I.1.3.2.2 Numere reale.

Numerele reale pot fi reprezentate in calculator prin doua metode:

Metoda de reprezentare a numerelor in virgula fixa. Pentru reprezentarea numerelor in virgula fixa se fac cateva conventii simple si anume:

à          Primul bit din partea stanga va fi bitul de semn;

à          Se foloseste un numar constant de pozitii binare pentru reprezentarea partii intregi a numarului;

à          Celelalte pozitii binare se folosesc pentru reprezentarea partii fractionare.

De exemplu numarul x = 3.625 = 11.101₍₂₎ va avea reprezentarea in virgula fixa pe un octet astfel:

Daca incercam sa reprezentam pe un octet, in virgula fixa numarul vom obtine

care este de fapt reprezentarea numarului . Din exemplu reiese ca atunci cand se depaseste capacitatea de reprezentare a partii intregi, se obtine reprezentarea altui numar decat cel dorit.

Pentru a preveni depasirea capacitatii de reprezentare, virgula va trebui fixata imediat dupa pozitia semnului, deci in virgula fixa pot fi practic reprezentate numai numere subunitare.

Metoda de reprezentare a numerelor in virgula mobila. Pentru a reprezenta un numar real in virgula mobila, acesta trebuie scris intr-o forma normalizata, adica sub forma unui produs dintre un numar subunitar, cu prima cifra semnificativa diferita de 0, si o putere a bazei. Partea subunitara, numita mantisa, se obtine deplasand virgula zecimala in fata primei cifre semnificative. Exponentul bazei va fi egal cu numarul de pozitii peste care s-a deplasat virgula, precedat de semnul + daca deplasarea s-a facut de la dreapta la stanga, si de semnul - daca deplasarea s-a facut de la stanga la dreapta.

Daca dorim reprezentarea in virgula mobila pe 4octeti 4octeti=32biti), vom avea

à          primul bit este bitul de semn al numarului(0=pozitiv 1= negativ

à          urmatorii 7 biti reprezinta caracteristica. Aceasta se va calcula cu formula: (C=Exponent+64), cifra 64, delimitand astfel numerele subunitare de cela supraunitare.

à          Urmatorii 24 de biti(3 octeti) reprezinta mantisa.

Exemplu.      X=28.12=1C.1EB84₍₁₆₎=0.1C1EB84₍₁₆₎*16²

C=64+2=66=42₍₁₆₎

Observatia 1. Este important de inteles faptul ca reprezentarea in virgula mobila a numerele reale, in calculator, desi exprima un interval foarte mare de date, este o aproximatie, ce depinde de numarul de pozitii pe care il are mantisa. Aceasta deoarece in transformarea in binar a numerelor fractionare, se obtine in cele mai multe din cazuri, numere periodice in baza 2 sau cu foarte multe cifre, care evident nu incap in mantisa, fiind trunchiate.

Astfel, in exemplul de mai sus, observam ca ultima cifra din numarul in hexazecimal(4) a fost pierduta, deoarece nu avea loc in mantisa. Deci numarul , desi este un numar mic si cu putine cifre, in calculator va fi reprezentat de o aproximatie foarte apropiata a acestuia, ce depinde de marimea mantisei(6 cifre hexazecimale in cazul prezentat)

Observatia 2. In exemplul prezentat, aveam o mantisa de de biti, care ne va permite scrierea a cifre hexazecimale adica a adica si ceva cifre zecimale. Orice numar cu mai mult de 7 cifre semnificative, va fi trunchiat la acestea. Deci, in reprezentarea prezentata, nu vom putea exprima numere cu o precizie mai mare de 7 cifre.

Astfel, daca avem numarul el va fi reprezentat in virgula mobila ca:

I.1.4 Codificarea caracterelor. Codurile ANSI, ASCII, UNICODE.

Prin caracter, in informatica se intelege orice simbol care poate fi afisat (tiparit) pe o singura pozitie. Caractere sunt litere, cifre, semne speciale sau alte simboluri. Pentru a fi introduse in calculator, si caracterele trebuiesc codificate in numere, in sistem binar.

Problema cea mai importanta a sistemelor de codificare pentru caractere, este numarul de biti pe care il folosesc, deoarece functie de acesta se pot acorda coduri la un anumit numar de caractere.

Astfel codul EBCDIC(folosit acum cateva decenii in informatica) sau codul ANSI(folosit cel mai mult in momentul de fata), sunt coduri pe biti, deci pot reprezenta de caractere.

Standardul ANSI, contine coduri in intervalul . El este format practic din doua parti:

Ø      Primele de coduri( ) sunt atribuite caracterelor care se gasesc pe o tastatura US standard, reprezinta codul ASCII.

Dintre acestea primele sunt caractere de control, netiparibile, dar care pot avea efect in afisarea datelor. De exemplu:

à          caracterul cu codul 13, CR - retur de car, care produce trecerea la inceput de rand

à          caracterul cu codul 10, LF - rand nou, care produce trecerea randul urmator

à          caracterul cu codul 7, Bell semnal sonor

à          caracterul cu codul 8, Back Space - inapoi

à          caracterul cu codul 9, Tab - salt la urmatorul marcaj

Codul ASCII

Nota: codurile sunt date in

à          sistemul de numeratie zecimal - in celule, inaintea fiecarui caracter;

à          sistemul de numeratie hexazecimal - pe cele 2 margini, prima cifra hexazecimala pe primul rand / a doua cifra hexazecimala pe prima coloana.

Ø      Urmatoarele caractere ( ) corespund caracterelor speciale, diacriticelor, accente, simboluri valutare, litere in alfabete internationale etc.

Codul UNICODE. Acest cod, este reprezentat pe biti, deci poate codifica caractere. El s-a impus in prezent, deoarece globalizarea informaticii, datorata in special dezvoltarii extraordinare pe care a avut-o in ultimii ani reteaua INTERNET, a necesitat marirea numarului de caractere ale codului, cu cele care sa reprezinte literele din toate alfabetele(chinez, japonez, arab, etc.)

I.1.5 Codificarea valorilor booleene.

Valorile booleene, TRUE si FALSE, desi pot fi reprezentate pe un singur bit, datorita problemelor de adresare se codifica pe 8 biti sau chiar 16 biti, ca numerele intregi. In general se foloseste urmatoarea conventie:

TRUE - se codifica prin numarul

FALSE - se codifica prin orice cod diferit de numarul