Drumuri minime de sursa unica

Drumuri minime intr-un graf

Fiind dat un graf G=(V,E) orientat se considera o functie asociata w:E->X numita functie de cost.

Costul unui drum u..v este reprezentat de suma costurilor muchiilor de pe drumul u..v. De exemplu pentru graful din figura 1 exista mai multe drumuri intre nodurile 1 si 2:

• Drumul 1->2 ce are cost total w(1,2)=1;
• Drumul 1->3->5->2 ce are w(1,2)=2+8+7=17;
• Drumul 1->3->4->6->5->2 ce are w(1,2)=2+5+6+4+7=24;
• Drumul 1->6->5->2 ce are w(1,2)=3+4+7=14;

Scopul nostru este sa determinam drumul optim din punct de vedere al costului intre o sursa s si toate nodurile d unde dIV. In cazul in care dÏR(s), distanta dintre s si d va fi considerata infinita.

In functie de codomeniul X al functiei de cost w distingem cateva cazuri distincte. Vom vedea ca exista algoritmi diferiti pentru cazurile de mai jos.

1. X=[0,∞) - muchiile au costuri pozitive

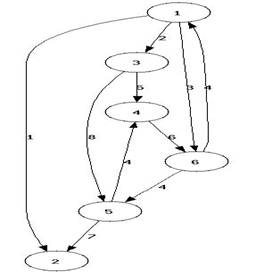
Figure 1 Graf cu muchii pozitive

Un exemplu de astfel de graf este o harta a unui oras unde sunt specificate distantele dintre diferitele intersectii

2. X=R - muchiile au costuri reale si nu exista cicluri de cost negativ

Un exemplu de astfel de graf poate sa apara in reprezentarea unor activitati economice unde pot sa apara muchii de cost negativ in cazul unor pierderi financiare

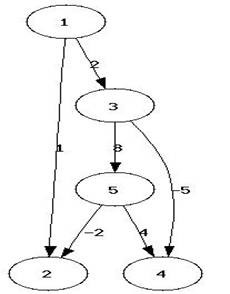
Figure 2 graf cu muchii reale dar fara ciclu de cost negativ

3. X=R - muchiile au costuri reale si exista cicluri de cost negativ

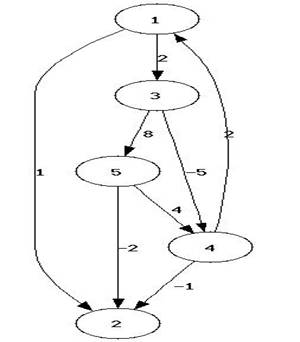
Figure 3 graf cu muchii reale si cu ciclu de cost negative

Prin ciclu de cost negativ intelegem un ciclu in care suma costurilor muchiilor ce fac parte din drum este negativa. In figura de mai sus drumul 1->3->4->1 are cost negativ. Se observa ca suma costurilor muchiilor de pe acest drum este negativa (2+5+(-2))=-1. Datorita acestui ciclu nu se poate obtine un cost minim pentru drumul (1,2) de exemplu deoarece la fiecare parcurgere a drumului de cost negativ costul drumului (1,2) mai scade cu o unitate. Astfel dupa n parcurgeri costul drumului (1,2) va fi n-2.

Algoritmul lui Dijkstra

Algoritmul lui Dijkstra se foloseste numai pentru grafuri orientate G=(V,E) pentru care exista o functie de cost asociata w:E->[0, ∞) - cazul 1 din cele prezentate de mai sus.

Algoritmul lui Dijkstra este un algoritm de tip Greedy. Optimul local ce se cauta este reprezentat de distanta dintre un nod sursa si un nod destinatie - distanta care este initializata cu infinit si apoi imbunatatita la fiecare pas. Imbunatatirea unei distante este realizata printr-un proces numit relaxare si functionarea acestui proces va fi exemplificata pe baza grafului din figura 4.

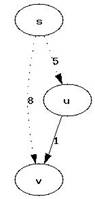
Figure 4 relaxarea muchiei u,v

In figura 4, in momentul in care se analizeaza muchia (u,v) exista un cost estimat pentru drumul s..v - d[v]=8 si un cost estimat pentru drumul s..u - d[u]=5. Se observa usor ca drumul dintre s..u..v este mai bun din punct de vedere al costului decat drumul s..v al carui cost este calculat pana in prezent deoarece d[v]>d[u]+w(u,v). Relaxarea consta in actualizarea d[v] in conditiile in care inegalitatea de mai sus este adevarata deoarece s-a gasit un drum evident mai bun in momentul de fata (am obtinut un optim local mai bun decat cel estimat la un pas precedent)

Pentru a tine evidenta muchiilor ce trebuie relaxate avem nevoie de 2 structuri - S - multimea de varfuri deja vizitate si Q - o coada cu prioritati - in sensul ca intotdeauna este extras elementul cu distanta fata de sursa cea mai mica

function Dijkstra(G, w, s)

for each vertex v in V[G]

d[v] := ∞ /* daca distanta intre s si un nod v nu este cunoscuta se initializeaza cu infinit. Astfel daca din s nu se poate ajunge in v distanta ramane infinit.*/

4 p[v] := null /*p[v] reprezinta nodul din care se va ajunge in v pe drumul cel mai scurt */

5 d[s] := 0 // distanta dintre s si s

6 S := Æ // S reprezinta multimea de varfuri deja vizitate

7 Q := V[G] /*Q reprezinta o coada cu prioritati in care sunt introduse varfurile care nu au fost vizitate*/

8 while Q Æ

9 u := Extract_Min(Q) /*se extrage din coada cu prioritati nodul a carui distanta fata de s este minima*/

S := S union //nodul se marcheaza ca fiind vizitat

11 for each (u,v) IAdj(u)

if d[u] + w(u,v) < d[v] // se relaxeaza muchia (u,v)

13 d[v] := d[u] + w(u,v)

14 p[v] := u

In cazul in care ne intereseaza doar drumul optim intre sursa s si o destinatie d putem opri cautarea la linia 9 daca s=d. Ulterior putem gasi cel mai scurt drum dintre s si d prin parcurgerea vectorului de parinti.

1 S := Æ

2 u := t

3 while p[u] null

adauga u la inceputul lui S

u := p[u]

Complexitatea algoritmului este O(|V|²+|E|) in cazul in care coada cu prioritati este implementata ca o cautare lineara si O(( | E | + | V | )log | V | ) in cazul in care implementam coada ca heap.

Algoritmul Bellman-Ford

Algoritmul BF poate fi folosit si pentru grafuri ce contin muchii de cost negativ dar nu poate fi folosit pentru grafuri ce contin cicluri de cost negativ (deci doar cazurile 1,2)

Algoritmul foloseste acelasi mecanism de relaxare ca si Dijkstra dar spre deosebire de acesta nu optimizeaza o solutie folosind un criteriu de optim local ci parcurge fiecare muchie de un numar de ori egal cu numarul de noduri si incearca sa o relaxeze de fiecare data pentru a imbunatati distanta pana la nodul destinatie al muchiei curente

Daca la sfarsitul acestor E*V relaxari mai poate fi imbunatatita o distanta atunci graful are un ciclu de cost negativ si nu poate fi aplicat algoritmul in acest caz. Cand este actualizata o distanta se actualizeaza automat si parintele nodului a carui distanta este actualizata

1. function BellmanFord(G,s) //G=(V,E), s=sursa

2. for each v in V[G]

d[v]= ∞;

p[v]=null;

5. for i = 1 to |V| 

for each (u,v) in E[G]

if d[v]>d[u]+w(u,v)

d[v]=d[u]+w(u,v);

p[v]=u;

10.for each (u,v) in E[G]

if d[v]>d[u]+w(u,v)

fail ("ciclu negativ");

Complexitatea algoritmului este in mod evident O(|E|*|V|)

Exemple

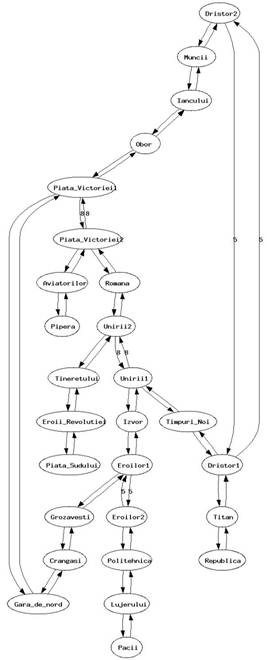
Graful generat mai jos este creat cu graphviz si va fi folosit in aplicatia de la laborator.

Resurse

https://en.wikipedia.org/wiki/Dijkstra's_algorithm

https://en.wikipedia.org/wiki/Bellman-Ford_algorithm

T. Cormen, C. Leiserson, R. Rivest, C. Stein - Introducere in Algoritmi

C. Giumale - Introducere in analiza algoritmilor