| CATEGORII DOCUMENTE |
ELEMENTE DE TEORIA GRAFURILOR
In orasul Knigsberg(Kalingrad) existau peste raul Pregel sapte poduri(fig ). Problema celor sapte poduri era:
Se poate face o plimbare peste toate cele sapte poduri, trecand o singura data peste fiecare pod?
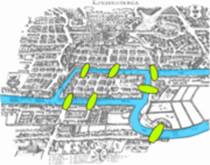
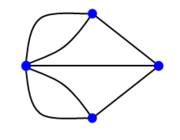
Fig. 1
Notiuni generale
In scopul descrierii unor activitati din cadrul unui proces de productie sau a relatiilor existente intre elementele unei structuri organizatorice se pot folosi imagini grafice gen diagrame, schite, grafice etc. O reprezentare dintre cele mai utilizate este cea prin grafuri. Acestea sunt utilizate in special pentru vizualizarea sistemelor si situatiilor complexe.
In general, vom reprezenta
-componentele acestora prin puncte in plan
-relatiile (legaturile, dependentele, influentele etc) dintre componente prin arce de curba cu extremitatile in punctele corespunzatoare.
Intre doua puncte pot exista unul sau mai multe segmente (in functie de cate relatii dintre acestea, care ne intereseaza, exista) iar segmentelor li se pot asocia sau nu orientari (dupa cum se influenteaza cele doua componente intre ele), numere care sa exprime intensitatea relatiilor dintre componente etc.
Definitia a)Se numeste multigraf un triplet G = (X, A, f)
in care X si A sunt doua multimi iar f este o functie ![]() definita pe produsul vectorial al lui X cu el
insusi (X2 = X X), care ia valori in multimea
partilor multimii A (notata P(A)).
definita pe produsul vectorial al lui X cu el
insusi (X2 = X X), care ia valori in multimea
partilor multimii A (notata P(A)).
b)Multimea X se numeste multimea nodurilor multigrafului si elementele sale se numesc noduri (sau varfuri) ale multigrafului, iar A reprezinta multimea relatiilor (legaturilor) posibile intre doua noduri ale multigrafului.
Definitia a)Se numeste graf orientat un multigraf in care multimea A are un singur element: A = .(In acest caz multimea partilor multimii A are doar doua elemente: multimea vida si intreaga multime A).
b)Daca unei perechi orientate (xi, xj) din X2 i se asociaza prin functia f multimea A atunci spunem ca exista arc de la nodul xi la nodul xj iar perechea (xi,xj) se va numi arcul (xi,xj).
c)Nodul xi se numeste nod initial sau extremitate initiala a arcului (xi,xj) iar nodul xj se numeste nod final sau extremitate finala a arcului (xi,xj).
d)Arcul (xi,xj) este incident spre interior varfului xj si incident spre exterior varfului xi.
e)Daca pentru un arc nodul initial coincide cu nodul final atunci acesta se numeste bucla.
f)Nodurile xi si xj se vor numi adiacente daca exista cel putin unul din arcele (xi,xj) si (xj,xi).
g) Daca unei perechi orientate (xi, xj) din X2 i se asociaza prin functia f multimea vida atunci spunem ca nu exista arc de la nodul xi la nodul xj.
Este evident ca a cunoaste un graf orientat este echivalent cu a cunoaste varfurile si arcele sale. Din acest motiv putem defini un graf orientat prin perechea (X,U), unde X este multimea varfurilor sale iar U multimea arcelor sale.
De asemenea, putem cunoaste un graf orientat cunoscand multimea nodurilor si, pentru fiecare nod, multimea arcelor incidente spre exterior. Din acest motiv putem defini un graf orientat ca o pereche (X,G) unde X este perechea nodurilor iar G este o functie definita pe X cu valori in multimea partilor lui X, valoarea acesteia intr-un nod xi, G(xi) X fiind multimea nodurilor adiacente nodului xi, prin arce pentru care xi este extremitatea initiala
Definitia Se numeste graf neorientat un multigraf in care multimea A are un singur element iar functia f are proprietatea:
f[(xi,xj)] = f[(xj,xi)] , oricare ar fi nodurile xi si xj din X
In aceste conditii, daca f[(xi,xj)] = f[(xj,xi)] = A atunci perechea neorientata este o muchie iar daca f[(xi,xj)] = f[(xj,xi)] = spunem ca nu exista muchie intre varfurile xi si xj.
Deoarece, in cele mai multe din cazurile practice care vor fi analizate in acest capitol, situatia este modelata matematic printr-un graf orientat, vom folosi, pentru simplificarea expunerii, denumirea de graf in locul celei de graf orientat iar in cazul in care graful este neorientat vom specifica acest fapt la momentul respectiv.
Moduri de reprezentare ale unui graf
A. O prima modalitate de reprezentare este listarea efectiva a tuturor nodurilor si a arcelor sale.
B. Putem reprezenta graful dand pentru fiecare nod multimea nodurilor cu care formeaza arce in care el este pe prima pozitie.
C. Putem reprezenta geometric graful, printr-un desen in plan, reprezentand fiecare nod printr-un punct(cerculet) si fiecare arc printr-un segment de curba care are ca extremitati nodurile arcului si pe care este trecuta o sageata orientata de la nodul initial spre cel final.
D. Putem folosi o reprezentare geometrica in care nodurile sunt reprezentate de doua ori, in doua siruri paralele, de la fiecare nod din unul din siruri plecand sageti spre nodurile cu care formeaza arce in care el este pe prima pozitie, de pe al doilea sir (reprezentarea prin corespondenta).
E. Un graf poate fi reprezentat printr-o matrice patratica booleana, de dimensiune egala cu numarul de noduri, in care o pozitie aij va fi 1 daca exista arcul (xi,xj) si 0 in caz contrar, numita matricea adiacentelor directe.
F. Un graf poate fi reprezentat printr-o matrice patratica latina, de dimensiune egala cu numarul de noduri, in care pe o pozitie aij va fi xixj daca exista arcul (xi,xj) si 0 in caz contrar.
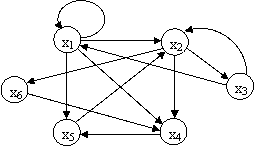 Exemplu: Daca in reprezentarea A avem graful G =
(X,U), unde X = si U = , atunci in celelalte reprezentari vom avea:
Exemplu: Daca in reprezentarea A avem graful G =
(X,U), unde X = si U = , atunci in celelalte reprezentari vom avea:
B) x1 C)
x2
x3
x4
x5
x6
D (reprezentarea prin corespondenta)
 x1 x2 x3 x4 x5 x6
x1 x2 x3 x4 x5 x6
x1 x2 x3 x4 x5 x6
x1
x2
x3
x4
x5
x6
x1
x2
x3
x4
x5
x6
x1
x2
x3
x4
x5
x6
x1
x1x1
x1x2
x1x4
x1x5
x2
x2x3
x2x4
x2x6
x3
x3x1
x3x2
x4
x4x5
x5
x5x2
x6
x6x4
Concepte de baza in teoria grafurilor
semigraf interior al unui nod xk: este multimea arcelor ![]() = care sunt incidente spre interior nodului
xk;
= care sunt incidente spre interior nodului
xk;
semigraf exterior al unui nod xk: este multimea arcelor ![]() = care sunt incidente spre exterior nodului
xk;
= care sunt incidente spre exterior nodului
xk;
semigradul interior al unui nod xk: este numarul arcelor care sunt
incidente spre interior nodului xk = cardinalul lui ![]() si se noteaza cu
si se noteaza cu ![]() ;
;
semigradul exterior al unui nod xk: este numarul arcelor care sunt
incidente spre exterior nodului xk = cardinalul lui ![]() si se noteaza cu
si se noteaza cu ![]() ;
;
gradul
unui nod xk: este suma semigradelor nodului xk: ![]() =
= ![]() +
+ ![]() ;
;
nod izolat: este un nod cu gradul 0;
nod suspendat: este un nod cu gradul 1;
arce adiacente: arce care au o extremitate comuna;
drum intr-un graf: o multime ordonata de noduri ale grafului: (x1, x2, , xk), cu proprietatea ca exista in graf toate arcele de forma (xi,xi+1) i = 1,,k-1;
lungimea unui drum: este numarul arcelor care il formeaza;
drum elementar: un drum in care fiecare nod apare o singura data;
drum simplu: un drum in care fiecare arc apare o singura data;
putere de atingere a unui nod xi I X in graful G: numarul de
noduri la care se poate ajunge din xi. Puterea de atingere se
noteaza cu p(xi), 1 i n si evident p(xi) ![]() .
.
drum hamiltonian: un drum elementar care trece prin toate nodurile grafului;
drum eulerian: un drum simplu care contine toate arcele grafului;
lant: un drum in care arcele nu au neaparat acelasi sens de parcurgere;
circuit: un drum in care nodul initial coincide cu cel final;
circuit elementar: un drum in care fiecare nod apare o singura data, cu exceptia celui final, care coincide cu cel initial;
circuit simplu: un drum in care fiecare arc apare o singura data;
circuit hamiltonian: un circuit care trece prin toate nodurile grafului;
ciclu: este un circuit in care arcele nu au neaparat acelasi sens de parcurgere;
ciclu elementar: un ciclu in care fiecare nod apare o singura data, cu exceptia celui final, care coincide cu cel initial;
ciclu simplu: un ciclu in care fiecare arc apare o singura data;
Observatie: Intr-un graf neorientat notiunile de drum si lant sunt echivalente si de asemenea cele de circuit si ciclu.
graf partial al unui graf G = (X,U): este un graf G'(X,U') cu U' U;
subgraf al unui graf G = (X,G): este un graf G'(X',G') unde X' X si G'(xi) = G(xi) X' pentru orice xi I X';
graf redus al unui graf G = (X,U): este un graf G*(X*,U*)
unde X* este formata din multimile unei partitii de
multimi nevide ale lui X, iar (![]() ,
,![]() ) exista doar daca i j si exista cel putin
un arc in U, de la un nod din
) exista doar daca i j si exista cel putin
un arc in U, de la un nod din ![]() la un nod din
la un nod din ![]() .
.
graf tare conex: este un graf in care intre oricare doua noduri exista cel putin un drum;
graf simplu conex: este un graf in care intre oricare doua noduri exista cel putin un lant;
Observatie: Pentru grafuri neorientat notiunile de tare conex si simplu conex sunt echivalente, graful numindu-se doar conex;
componenta tare conexa a unui graf G = (X,U): este un subgraf al lui G care este tare conex si nu este subgraful nici unui alt subgraf tare conex al lui G (altfel spus, intre oricare doua noduri din componenta exista cel putin un drum si nu mai exista nici un nod in afara componentei legat printr-un drum de un nod al componentei).
Gasirea drumurilor intr-un graf orientat
Pasul 1. Se construieste matricea booleana a adiacentelor directe corespunzatoare grafului, notata cu A. In aceasta se afla, evident, toate drumurile de lungime 1.
Este interesant de vazut ce legatura exista intre aceasta matrice si drumurile de lungime 2. Fie doua noduri xi si xj oarecare din graf. Existenta unui drum de lungime 2 intre ele presupune existenta unui nod xk, din graf, cu proprietatea ca exista atat arcul (xi,xk) cat si arcul (xi,xk). Pentru a vedea daca acesta exista, luam pe rand fiecare nod al grafului si verificam daca exista sau nu ambele arce ((xi,xk) si (xi,xk)). Aceasta este echivalent cu a verifica daca, in matricea booleana a adiacentelor directe, exista vreun indice k astfel incat elementul k al liniei i si elementul k al coloanei j sa fie ambele egale cu 1. Daca folosim operatiile algebrei booleene de adunare si inmultire:
|
|
| |||||
atunci verificarile de mai sus sunt echivalente cu a verifica daca elementul de pe pozitia (i,j) din A2 este egal cu 1. Valoarea 1 spune doar ca exista cel putin un drum de lungime 2 de la xi la xj. Daca dorim sa vedem si cate sunt, vom folosi regulile de inmultire si adunare obisnuita.
De asemenea, se poate observa ca existenta unui drum de lungime 3 de la xi la xj presupune existenta unui nod xk astfel incat sa existe un drum de lungime 2 de la xi la xk si un arc de la xk la xj, care este echivalent cu a verifica daca exista vreun indice k astfel incat elementul k al liniei i din matricea A2 si elementul k al coloanei j din A sunt ambele egale cu 1 sau, mai simplu, daca elementul (i,j) din A3 este 1.
Din cele de mai sus se observa ca existenta drumurilor de lungime k este data de valorile matricei Ak, daca s-au folosit regulile algebrei booleene si numarul lor este dat de Ak, daca s-au folosit regulile obisnuite.
Pasul 2. Vom calcula succesiv puterile lui A pana la puterea An-1
Daca intre nodurile xi si xj exista un drum de lungime n atunci el va contine un numar de noduri mai mare sau egal nu n+1 si, cum in graf sunt doar n varfuri, este clar ca cel putin unul, sa zicem xk, va aparea de doua ori. Vom avea in acest caz un drum de la xi pana la prima aparitie a lui xk, si un drum de la ultima aparitie a lui xk la xj. Eliminand toate nodurile dintre prima aparitie a lui xk si ultima aparitie a sa vom obtine un drum de la xi la xj, in care xk apare o singura data. Aplicand acest procedeu pentru toate nodurile care apar de mai multe ori pe drum, vom obtine un drum de la xi la xj, in care fiecare nod apare o singura data (deci un drum elementar), care are evident cel mult n-1 arce. In concluzie, daca exista vreun drum de la xi la xj atunci exista si un drum elementar si, deci, va exista o putere a lui A, intre A1 si An-1, in care pozitia (i,j) este diferita de 0. Pentru deciderea existentei unui drum intre oricare doua noduri este suficienta, deci, calcularea doar a primelor n-1 puteri ale lui A.
Pasul 3. Se calculeaza matricea D = A + A2 + + An-1
Daca ne intereseaza doar existenta drumurilor dintre noduri, nu si numarul lor, vom folosi inmultirea si adunarea booleana si conform observatiei de mai sus:
dij
= ![]()
In acest caz, observand ca:
A (A + I)n-2 = ![]() A +
A +![]() A2
+
A2
+ ![]() A3
+ +
A3
+ + ![]() An-1
= A + A2 + A3 + + An-1 = D
An-1
= A + A2 + A3 + + An-1 = D
rezulta ca e suficient sa calculam doar puterea n-2 a matricei A + I si apoi s-o inmultim cu A. Avantajul acestei metode, in ceea ce priveste economia de timp, este sustinut si de urmatoarea observatie: daca D contine toate perechile de arce intre care exista drum atunci:
D = (A + A2 + + An-1) + An + An+1 + + An+k = D oricare ar fi k 0 T
T A (A + I)n-2+k = (A + A2 + + An-1) + An + An+1 + + An+k-1 = D = A (A + I)n-2
A (A + I)n-2+k = A (A + I)n-2 oricare ar fi k
deci de la puterea k = n-2 toate matricile Ak
sunt egale. Putem, deci, calcula direct orice putere a lui A+I mai mare sau
egala cu n-1 (de exemplu calculand (A+I)2, (A+I)4,
(A+I)8, , ![]() , r fiind prima putere a lui 2 pentru care 2r
n-2).
, r fiind prima putere a lui 2 pentru care 2r
n-2).
Procedeul de mai sus nu asigura decat aflarea faptului daca exista sau nu drum intre doua noduri, eventual ce lungime are si cate sunt de aceasta lungime. Totusi, in problemele practice cel mai important este sa stim care sunt efectiv aceste drumuri. Deoarece toate drumurile pot fi descompuse in drumuri elementare si in problemele practice in general acestea sunt cele care intereseaza, pasii urmatori ai algoritmului vor fi dedicati gasirii lor.
Pentru gasirea acestora se foloseste reprezentarea grafului prin matricea latina de la cazul F.
Pasul 4. Construim matricea latina L asociata grafului, unde:
lij
= ![]()
si matricea ![]() , definita prin:
, definita prin:
![]() =
= ![]()
numita matricea latina redusa.
Gasirea unui drum de lungime 2 de la xi la xj
presupune gasirea unui nod cu proprietatea ca exista arcele (xi,xk)
si (xk,xj) si memorarea vectorului (xi,
xk, xj). Aceasta este echivalent cu a gasi un indice
k astfel incat elementul de pe pozitia k a liniei i, din matricea L,
sa fie xi,xk si elementul de pe pozitia k
al coloanei j, din matricea ![]() , sa fie xj. Vom inmulti deci
matricea L cu matricea
, sa fie xj. Vom inmulti deci
matricea L cu matricea ![]() , folosind insa niste reguli de calcul
speciale, numite inmultire si adunare latina.
, folosind insa niste reguli de calcul
speciale, numite inmultire si adunare latina.
Definitia 1: Se numeste alfabet o multime de semne numite simboluri sau litere unde I este o multime oarecare de indici, finita sau nu.
Definitia 2: Se numeste cuvant
un sir finit de simboluri notat ![]() .
.
Definitia 3: Se numeste inmultire
latina o operatie definita pe multimea cuvintelor unui
alfabet, notata '![]() ', astfel:
', astfel:
![]()
![]()
![]() =
= ![]()
(produsul a doua cuvinte se obtine prin concatenarea lor)
Inmultirea latina este asociativa, are ca element neutru cuvantul vid, nu e comutativa si un element este inversabil doar daca este cuvantul vid.
Definitia 3: Se numeste adunare
latina o functie definita pe multimea cuvintelor unui
alfabet cu valori in multimea partilor multimi cuvintelor,
notata '![]() ' astfel:
' astfel:
![]()
![]()
![]() =
= 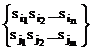
(suma a doua cuvinte este multimea formata din cele doua cuvinte)
Pasul 5. Se calculeaza succesiv matricile:
L2
= L![]()
![]() , L3 = L2
, L3 = L2![]()
![]() , ,Lk+1 = Lk
, ,Lk+1 = Lk![]()
![]()
folosind operatiile de inmultire si adunare latina, alfabetul fiind multimea nodurilor grafului, unde operatia de inmultire este usor modificata, produsul dintre doua elemente ale matricilor fiind 0, daca unul dintre ele este 0 sau au un nod comun si este produsul latin al lor, in caz contrar.
Din felul cum a fost construita, matricea Lk va contine toate drumurile elementare de lungime k. Cum un drum elementar poate avea cel mult n noduri (cate are graful cu totul) rezulta ca:
primele n-1 puteri ale lui L contin toate drumurile elementare din graf;
puterile lui L mai mari sau egale cu n au toate elementele egale cu 0;
matricea Ln-1 contine toate drumurile hamiltoniene din graf (daca exista).
Observatie: Deoarece obtinerea matricii D prin metoda de mai sus presupune un volum foarte mare de calcule (de exemplu, daca graful are 100 de noduri, ridicarea unei matrici de 100100 la puterea 100) pentru obtinerea acesteia se poate aplica si urmatorul algoritm:
Pas 1. Se construieste matricea de adiacenta A;
Pas 2. Pentru fiecare linie i se aduna boolean la aceasta toate liniile j pentru care aij = 1.
Pas 3. Se reia pasul 2 pana cand, dupa o aplicare a acestuia, matricea ramane aceeasi (nu mai apare nici un 1)
Ultima matrice obtinuta este matricea drumurilor D numita si matricea conexiunilor totale.
Aceasta metoda, desi mai simpla nu spune insa si care sunt aceste drumuri, pentru gasirea lor aplicandu-se, de exemplu, inmultirea latina
Drumuri si circuite hamiltoniene
Una dintre cele mai cunoscute probleme economice este problema comis voiajorului. Comis voiajorul este un individ care trebuie sa prezinte s-au sa distribuie marfa comandata la o serie de centre distribuite in general neliniar pe o anumita zona teritoriala (localitatile dintr-un judet, magazinele dintr-un cartier, persoanele dintr-un sat etc). Daca numarul de obiective care trebuie vizitate este mare sau foarte mare iar timpul disponibil foarte limitat atunci devine vitala o asemenea organizare a trecerii pe la fiecare obiectiv incat sa se efectueze in timpul minim posibil. Acest timp minim se traduce prin drumul cel mai scurt, iar cel mai scurt drum este evident cel in care se trece pe la fiecare obiectiv o singura data. In plus, la sfarsit trebuie sa se afle in punctul initial, adica sediul firmei la care lucreaza.
O reprezentare a regiunii aprovizionate, in care centrele pe la care se trece sunt vizualizate prin puncte iar caile de acces la acestea prin segmente de curbe, va fi evident un graf, problema reducandu-se la a gasi circuitul hamiltonian de lungime minima.
In timp, s-au evidentiat o multitudine de probleme reductibile la gasirea unui drum (sau circuit) hamiltonian intr-un graf, cum ar fi:
Problema postasului (gasirea traseului cel mai scurt care trece pe la toate locuintele ce apartin de oficiul postal la care lucreaza acesta);
Problema adunarii deseurilor (cel mai scurt drum care trece pe la toate punctele de depozitate a deseurilor);
Problema succesiunii operatiilor (executarea mai multor operatii pe o masina in acea ordine in care suma timpilor consumati cu pregatirea masinii pentru trecerea de la o operatie la urmatoarea sa fie minim)
Ordinea lipirii unor componente electronice pe o placa, etc;
Determinarea drumurilor hamiltoniene
Problema determinarii drumului (circuitului) hamiltonian de valoare optima s-a dovedit deosebit de dificila, neexistand nici acum un algoritm care sa rezolve problema in timp polinomial si nici macar o metoda simpla prin care sa se decida daca intr-un graf dat exista sau nu drumuri hamiltoniene.
Exista insa mai multi algoritmi, care reusesc, intr-un caz sau altul, sa rezolve problema satisfacator si in timp util.
A. Algoritmul lui Foulkes
Pasul 1. Se scrie matricea booleana A asociata grafului G.
Pasul 2. Se determina matricea D a drumurilor grafului G prin procedeul expus la inceputul capitolului si apoi matricea M = I + D.
Pasul 3. Se imparte multimea nodurilor grafului in submultimi disjuncte astfel:
Se considera in matricea M liniile pline (cu toate elementele 1). Nodurile ce corespund liniilor pline cu 1 formeaza submultimea C1.
Se elimina liniile si coloanele care corespund nodurilor din submultimea stabilita.
Se reia rationamentul de la punctul 1 pe matricea redusa obtinuta la punctul 2 obtinandu-se urmatoarea submultime si in continuare toate celelalte pana se epuizeaza toate liniile matricei.
Pasul 4. Se construieste graful G' in care:
Nodurile care formeaza o submultime sunt reprezentate prin puncte in interiorul unui dreptunghi si intre acestea se traseaza arcele existente in graful initial G.
Se traseaza legaturile dintre submultimi. Ele sunt reprezentate prin arcele existente in graful initial G intre nodurile submultimii C1 si cele ale submultimii C2, intre nodurile submultimii C2 si cele ale submultimii C3 etc.
Pasul 5. Se gasesc drumurile hamiltoniene
Un drum hamiltonian se gaseste plecand de la un varf din submultimea C1, trecand prin toate varfurile acesteia cu un drum hamiltonian, din ultimul varf la care se ajunge in C1 trecand la un varf din C2, parcurgand in continuare un drum hamiltonian in a doua submultime si tot asa, trecand prin toate submultimile si parcurgand, deci, toate nodurile grafului initial, o singura data. Aplicand acest procedeu in toate modurile posibile se obtin toate drumurile hamiltoniene din graful initial G. (Observatie: poate sa nu existe nici un drum hamiltonian in graful G, caz in care algoritmul se opreste deoarece la un anumit pas nu mai exista nici o linie plina cu 1).
Observatie. Algoritmul lui Foulkes reduce gasirea drumurilor hamiltoniene in graful initial G (care in problemele practice este foarte mare) la gasirea mai multor drumuri hamiltoniene mai mici in componente tare conexe ale grafului. Daca un graf are o singura componenta tare conexa, algoritmul lui Foulkes nu este eficient, in acest caz trebuind aplicati alti algoritmi cum ar fi cel bazat pe inmultirea latina.
B. Algoritmul lui Chen pentru determinarea drumurilor hamiltoniene in grafuri fara circuite-tema referat
C. Algoritmul lui Kaufmann
Pasul 1. Construim matricea latina L asociata grafului, unde:
lij
= ![]()
Pasul
2. Construim matricea ![]() , definita prin:
, definita prin:
![]() =
= ![]()
numita matricea latina redusa.
Pasul 3. Se calculeaza succesiv matricile:
L2
= L![]()
![]() , L3 = L2
, L3 = L2![]()
![]() , , Lk+1 = Lk
, , Lk+1 = Lk![]()
![]() ,
,
folosind operatiile de inmultire si adunare latina, alfabetul fiind multimea nodurilor grafului, unde operatia de inmultire este usor modificata, produsul dintre doua elemente ale matricilor fiind 0, daca unul dintre ele este 0 sau au un nod comun, si este produsul latin al lor, in caz contrar.
Din felul cum a fost construita, matricea Lk va contine toate drumurile elementare de lungime k. Cum un drum elementar poate avea cel mult n noduri (cate are graful cu totul) rezulta ca:
primele n-1 puteri ale L contin toate drumurile elementare din graf;
puterile lui L mai mari sau egale cu n au toate elementele egale cu 0;
matricea Ln-1 contine toate drumurile hamiltoniene din graf.
Pasul 4. Daca se doresc si circuitele atunci se verifica pentru fiecare drum hamiltonian daca poate fi completat pana la un circuit (adica daca exista in graf arcul care uneste nodul final cu cel initial);
Pasul 5. Daca se doreste si drumul (sau circuitul) de valoare optima (maxima sau minima) se calculeaza suma valorilor pentru fiecare drum si/sau circuit si se alege cel cu valoarea optima.
In concluzie, metoda inmultirii latine (A. Kaufmann - J. Melgrange) determina toate drumurile elementare din graf, prin calcularea matricelor M(1), M(2), M(3), ., M(n-1).
In matricea M(n-1) se citesc drumurile hamiltoniene.
Aceasta metoda a inmultirii latine (algoritmul lui Kaufmann) este utila, mai ales, in cazul grafurilor tare conexe, unde algoritmul lui Foulkes nu este eficient. Totusi, metoda este greu de aplicat in grafuri cu un numar mare de noduri. In acest caz este preferabil sa se construiasca graful condensat, sa se determine drumurile hamiltoniene in fiecare in parte cu algoritmul lui Kaufmann si apoi, ca la algoritmul lui Foulkes, sa se caute drumurile hamiltoniene in graful initial.
D. Un algoritm bazat pe algoritmul ungar-tema referat
6. Drumuri optime intr-un graf
In marea majoritate a problemelor care pot fi modelate prin grafuri nu ne intereseaza numai daca exista sau nu legaturi intre componentele reprezentate prin nodurile grafului ci si intensitatea acestora. Aceasta intensitate are semnificatia unei valori numerice (pozitive sau negative) asociate arcului corespunzator legaturii a carei intensitate o masoara.
In aplicatiile economice aceasta valoare poate fi:
lungimea drumului dintre doua localitati;
costul parcurgerii rutei reprezentate prin arcul corespunzator;
durata parcurgerii rutei respective;
cantitatea transportata pe ruta respectiva;
capacitatea maxima a rutei respective;
castigul realizat prin trecerea de la o stare la alta a sistemului;
consum de energie pentru efectuarea trecerii respective;
punctaj realizat etc.
Una din problemele care poate aparea in aceste situatii este gasirea, pentru o anumita pereche de noduri (sau mai multe perechi), a drumului optim intre acestea.
Pentru formalizarea problemei vom introduce notiunea de valoare a unui drum, care este egala cu suma valorilor arcelor care il compun. Vom nota in continuare valoarea unui arc (xi,xj) cu v(xi,xj) sau cu vij. In aceste conditii putem enunta problema drumului optim astfel:
'Dat un graf G = (X,U) si o functie care asociaza fiecarui arc o valoare reala, sa se gaseasca, pentru o pereche data de noduri, drumul (drumurile) de valoare optima (minima sau/si maxima) intre cele doua noduri si valoarea acestuia (acestora)'
Deoarece este vorba de gasirea minimului unei multimi de numere reale, prima intrebare care se pune este daca aceasta admite minim. Daca multimea nodurilor grafului este infinita atunci pot exista o infinitate de drumuri elementare distincte intre cele doua noduri si multimea valorilor acestora poate avea orice forma (inchisa sau nu, marginita sau nu) devenind foarte greu de caracterizat cazurile cand minimul dorit exista. Deoarece totusi majoritatea covarsitoare a problemelor economice se modeleaza prin grafuri cu numar finit de noduri, ne vom limita in continuare doar la acestea.
Un numar finit
de noduri n atrage dupa sine existenta unui numar finit
de arce (cel mult n2) si a unui numar finit de drumuri
elementare ( cel mult n n! ![]() ). Deoarece oricarui drum d ii corespunde un drum elementar
de (obtinut prin eliminarea tuturor
subcircuitelor lui d) putem calcula valoarea oricarui drum ca
suma intre valoarea drumului elementar corespunzator si valorile
unor subcircuite ale sale, fiecare
inmultita cu numarul de parcurgeri ale circuitului respectiv.
). Deoarece oricarui drum d ii corespunde un drum elementar
de (obtinut prin eliminarea tuturor
subcircuitelor lui d) putem calcula valoarea oricarui drum ca
suma intre valoarea drumului elementar corespunzator si valorile
unor subcircuite ale sale, fiecare
inmultita cu numarul de parcurgeri ale circuitului respectiv.
In concluzie, daca exista un circuit de valoare negativa inseamna ca exista drumuri de valoare oricat de mica (cele care contin acest circuit), obtinuta prin parcurgerea acestuia de oricate ori dorim) si, deci, multimea valorilor drumurilor este nemarginita inferior, neexistand drum de valoare minima. Daca exista un circuit de valoare pozitiva atunci exista drumuri de valoare oricat de mare si multimea valorilor drumurilor este nemarginita superior, neexistand drum de valoare maxima.
Daca nu exista circuite de valoare negativa atunci valoarea oricarui drum este mai mare sau egala cu a drumului elementar corespunzator, deci drumul de valoare minima (daca exista) va fi un drum elementar. Cum multimea drumurilor elementare este finita (si deci si multimea valorilor lor) va avea minorant si am lamurit problema compatibilitatii problemei. Analog, daca nu exista circuite de valoare pozitiva atunci valoarea oricarui drum este mai mica sau egala cu a drumului elementar corespunzator, deci drumul de valoare maxima (daca exista) va fi un drum elementar. Cum multimea drumurilor elementare este finita (si deci si multimea valorilor lor), va avea majorant.
Obs. 1. Daca in graf nu exista decat arce de valoare pozitiva atunci exista drum de valoare minima.
Obs. 1. Daca in graf nu exista decat arce de valoare negativa atunci exista drum de valoare maxima.
Obs. 1. Daca in graf nu exista circuite atunci exista si drum de valoare minima si drum de valoare maxima.
Deoarece din cele de mai sus se sesizeaza importanta existentei circuitelor intr-un graf vom da in continuare un algoritm de depistare a existentei circuitelor intr-un graf:
Pasul 1. Se construieste multimea A formata din nodurile pentru care toate arcele incidente sunt incidente spre interior ( noduri in care toate arcele 'intra' sau, altfel spus, noduri din care nu 'pleaca' nici un arc).
Pasul 2. Se gasesc toate nodurile care nu sunt din A pentru care toate arcele incidente au cealalta extremitate in A (noduri din care se poate 'ajunge' doar in A). Daca nu exista nici un astfel de arc se trece la pasul 4.
Pasul 3. Se adauga arcele gasite la pasul 2 la multimea A apoi se reia algoritmul de la pasul 2, pentru noua multime A.
Pasul 4. Daca A contine multimea tuturor nodurilor atunci graful nu contine circuite. Daca au ramas noduri in afara lui A atunci graful contine circuite.
Algoritmi de gasire a drumului optim
Din cauza varietatii nelimitate a grafurilor posibile, nu exista un algoritm care sa rezolve orice problema in timp util, dar s-au elaborat o multime de algoritmi, fiecare fiind cel mai eficace in anumite cazuri. Acesti algoritmi pot fi grupati in cinci categorii:
Algoritmi prin calcul matricial (Bellman-Kalaba, I. Tomescu, Bellman-Schimbell);
Algoritmi prin ajustari succesive: (Ford);
Algoritmi prin inductie (Dantzig);
Algoritmi prin ordonare prealabila a varfurilor grafului;
Algoritmi prin extindere selectiva (Dijkstra).
1. Algoritmul lui Bellman - Kalaba
Algoritmul se aplica in grafuri finite care nu au circuite de valoare negativa (pentru o problema de minim) sau care nu au circuite de valoare pozitiva (intr-o problema de maxim) si gaseste drumurile de valoare minima (maxima) de la toate nodurile grafului la un nod oarecare, fixat. Daca dorim sa cunoastem drumurile de valoare minima (maxima) intre oricare doua noduri vom aplica algoritmul, pe rand, pentru fiecare nod al grafului.
Fie G = un graf orientat finit. Presupunem (fara a restrange generalitatea, ca am numerotat nodurile astfel incat nodul spre care cautam drumurile de valoare minima (maxima) de la celelalte noduri sa fie xn.
Pasul 1. Se construieste matricea patratica M cu dimensiunea egala cu numarul de noduri ale grafului ale carei elemente sunt:
mij
= 
Pasul 2. Se adauga succesiv liniile Li la matricea M, elementele acestora calculandu-se prin relatiile de recurenta:
L1j = mjn j = 1,,n (prima linie este ultima coloana, transpusa, a matricii M)
Lij
= min (Li-1,j , ![]() (mjk + Li-1,k)) intr-o problema de minim
(mjk + Li-1,k)) intr-o problema de minim
sau Lij
= max (Li-1,j , ![]() (mjk + Li-1,k)) intr-o problema de maxim
(mjk + Li-1,k)) intr-o problema de maxim
Pasul 3. Dupa calcularea fiecarei linii noi se compara elementele ei cu cele ale precedentei:
Daca Lij = Li-1,j pentru orice j = 1,,n atunci se opreste recurenta si ultima linie calculata contine valorile minime ale drumurilor de la celelalte noduri la nodul xn.
Daca exista cel putin un indice j cu Lij Li-1,j se trece la calcularea noii linii Li+1
Pasul 4. Pentru
gasirea drumului care da valoarea minima de la un nod xj
la nodul xn se gasesc, incepand inapoi de la ultima linie, pe
care s-au obtinut valorile finale, notata Lf, nodurile ![]() ,
,![]() , ,
, , ![]() care formeaza drumul cautat, unde
care formeaza drumul cautat, unde ![]() = xj,
= xj, ![]() = xn si fiecare alt indice ki+1
este cel pentru care s-a obtinut minimul(maximul) de pe pozitia ki
al liniei Li.
= xn si fiecare alt indice ki+1
este cel pentru care s-a obtinut minimul(maximul) de pe pozitia ki
al liniei Li.
Observatie: Pentru grafuri foarte mari, algoritmul necesita un volum mare de memorie, prin necesitatea memorarii matricei M, care este greu de manipulat. Chiar daca din cele n2 arce posibile graful ar avea doar un procent foarte mic matricea grafului va avea tot n2 pozitii de memorat si analizat.
Exemplu: Presupunem dat graful orientat de mai jos, in care se doreste gasirea drumului de valoare minima de la nodul x1 la nodul x9.
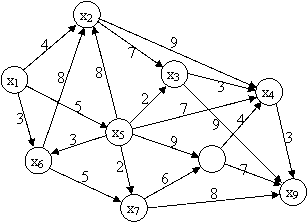
Matricea M va fi 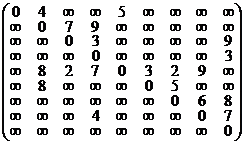
iar dupa calcularea liniilor Li obtinem:
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
x8 |
x9 |
|
|
x1 | |||||||||
|
x2 | |||||||||
|
x3 |
| ||||||||
|
x4 | |||||||||
|
x5 | |||||||||
|
x6 | |||||||||
|
x7 | |||||||||
|
x8 | |||||||||
|
x9 | |||||||||
|
L1 | |||||||||
|
L2 | |||||||||
|
L3 | |||||||||
|
L4 | |||||||||
|
L5 |
Deoarece L4 = L5 oprim calcularea liniilor dupa calcularea liniei 5. In aceasta linie se afla valorile celor mai scurte de la toate nodurile la nodul x9. Drumul dorit de noi (x1 x9) are valoarea data de prima pozitie a liniei 5, fiind egal cu 13.
Pentru a gasi acest drum, plecam inapoi de la linia 4 si avem:
|
|
x5 | |||||||
|
|
x3 | |||||||
|
| ||||||||
|
|
x4 |
|||||||
|
|
x9 |
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 4491
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved