| CATEGORII DOCUMENTE |
Cand valorile studiate variaza continuu, cum este cazul greutatii si inaltimii, al procentului de substanta umorala etc., adica atunci cand variabila poate lua toate valorile posibile intr-un interval dat, valorile observate pot fi foarte numeroase si distributia de frecventa este foarte dispersata. In acest caz este necesara reducerea numarului de valori posibile si pentru aceasta, se imparte domeniul de variatii posibile intr-un numar de intervale sau clase in interiorul carora se grupeaza toate valorile care cad in intervalul corespunzator.
Exemplul 2 Se studiaza distributia pe varste in acelasi lot de bolnavi oncologici. Varsta variaza intre 0 si 97 de ani. Se imparte domeniul de variatie in intervale de cate 10 ani, care constituie clase in interiorul carora se grupeaza toti subiectii a caror varsta este cuprinsa intre limitele intervalului; multimea acestor subiecti constituie efectivul clasei.
|
Clase x |
Efectiv F |
Frecventa f = F/n |
Procentajul 100 * f |
|
x <= 1 | |||
|
1 <= x <= 10 | |||
|
11 <= x <= 20 | |||
|
21 <= x <= 30 | |||
|
31 <= x <= 40 | |||
|
41 <= x <= 50 | |||
|
51 <= x <= 60 | |||
|
61 <= x <= 70 | |||
|
71 <= x <= 80 | |||
|
81 <= x <= 90 | |||
|
91 <= x <= 100 | |||
|
TOTAL |
n = 3709 |
Tabelul 8.2: Distributia pe varste a lotului de bolnavi oncologici
Intervalul de clasa
O importanta deosebita o are precizarea domeniului claselor alese, numit "interval de clasa", care trebuie sa fie acelasi pentru toate clasele iar intervalele de clasa trebuie sa fie alaturate si fara suprapuneri.
Intervalele de clasa se pot preciza in trei moduri (Figura 8.1, tabel 8.3):
Puncte mediane: 5.5 15.5 25.5 35.5 .
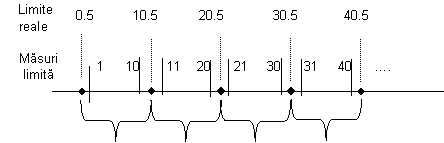
Figura 8.1: Alegerea intervalelor de clasa
Indicand, ca in exemplul precedent, masurile limita ale fiecarei clase, adica cea mai mica si cea mai mare masura inaintea apartenentei la clasa, tinand cont de precizia masuratorii.
Indicand ceea ce se numeste "limitele reale" ale fiecarei clase, adica cea mai mica si cea mai mare dintre valorile teoretice ale variabilei in aceasta clasa; de altfel, limita superioara a unei clase si limita inferioara a clasei urmatoare coincid, ca de exemplu valoarea 10.5 pentru clasele (0.5 .. 10.5) si (10.5 .. 20.5).
Indicand valoarea care se gaseste exact in centrul clasei, numita "punct median" al clasei, si care este data de semisuma limitelor unei clase, ca de exemplu 5.5, 15.5, 25.5 etc.
|
Masuri limita |
Limite reale |
Puncte mediane |
Efectiv F |
|
x = 0 |
x = 0 | ||
|
1 <= x <= 10 |
0.5 < x < 10.5 | ||
|
11 <= x <= 20 |
10.5 < x < 20.5 | ||
|
21 <= x <= 30 |
20.5 < x < 30.5 | ||
|
31 <= x <= 40 |
30.5 < x < 40.5 | ||
|
41 <= x <= 50 |
40.5 < x < 50.5 | ||
|
51 <= x <= 60 |
50.5 < x < 60.5 | ||
|
61 <= x <= 70 |
60.5 < x < 70.5 | ||
|
71 <= x <= 80 |
70.5 < x < 80.5 | ||
|
81 <= x <= 90 |
80.5 < x < 90.5 | ||
|
91 <= x <= 100 |
90.5 < x < 100.5 | ||
|
TOTAL |
n = 3709 |
Tabelul 8.3: Distributia pe varste a lotului de bolnavi oncologici
Grupand datele in clase, se remarca asimilarea tuturor valorilor unei clase la o valoare unica, aceea a punctului median (in acest mod, se face reducerea la cazul unei variabile discontinue).
Observatie: Experienta arata ca in practica numarul intervalelor de clasa este bine sa fie cuprins intre 10 si 20.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2206
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved