Problema Labirintului -

Liceul Teoretic "N. Jiga" Tinca

Specializare: matematica-informatica

Lucrare de atestat

Liceul Teoretic "N. Jiga" Tinca

Problema Labirintului

Cuprins:

Despre problema labirintului

Enuntul problemei

Rezolvarea problemei labirintului

Labirintul

Aplicatie la rezolvarea problemei

Program labirint

Bibliografie

Despre problema labirintului

Am ales aceasta problema deoarece m-a impresionat foarte mult si n-am gasit alta mai atractiva. Problema labirintului poate fi un joc pentru copii mai talentati deoarece este mai complicata. Pentru a o intelege trebuie studiata cu atentie. Este o problema de inteligenta.

Ca imbunatatiri pentru problema,recomandarea mea ar fi ca programul poate sa contina animatii pentru a intelege mai bine problema, culori pentru modul grafic si sunete pentru a te avertiza cand ai un obstacol pentru a merge pe traseul corect.

Enuntul problemei

Se da un labirint sub forma de matrice cu n linii si m coloane. Fiecare element al matricei se codifica cu 0 daca este zid sau cu 1 daca este culoar. Intr-un punct al labirintului, de coordonate (i,j) se gaseste o persoana. Deplasarea persoanei se poate face doar in directiile celor patru puncte cardinale: nord, sud, est, vest. Se cere sa se gaseasca toate iesirile din labirint.

Rezolvarea problemei labirintului

Vom folosi tehnica backtracking. Problema este tipica pentru aceasta tehnica, astfel incat tot ceea ce avem de facut este sa explicitam functiile care reprezinta testul de validitate si de finalitate ale unei solutii. Singura dificultate, aparenta insa, provine de la faptul ca stiva pe care o vom folosi este putin mai complicata. Sa ne aducem aminte ca prin stiva nu am inteles neaparat un vector, ci pur si simplu o structura de date, ordonata, in care operatiile de introducere sau extragere se fac la un singur cap. De obicei, am modelat o stiva printr-un vector, dar asta nu inseamna ca nu exista si astfel de stive ! Concret, stiva cu care vom lucra va cuprinde coordonatele punctelor parcurse pana la un moment dat.

Vom urmari mai usor explicatiile daca ne vom referi la un exemplu efectiv.

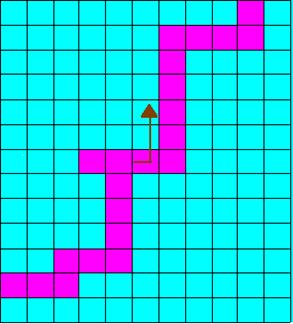
Astfel, sa consideram labirintul desenat pe pagina urmatoare: 

De exemplu, succesiunea: (7,6) (7,7) (6,7) (5,7) are semnificatia unui drum prin labirint inceput in punctul de coordonate (7,6) si continuat la dreapta cu o pozitie si apoi in sus cu doua pozitii. Corespunzator acestei situatii, stiva va contine valorile pe care le vom reprezenta in mod intuitiv prin :

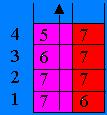
Stiva se va 'umple' pas cu pas, prin pozitii admisibile : cea mai de jos va fi nivelul 0 (initial) apoi 1, 2, etc.

Aplicatie

Inainte de a explicita functiile, sa precizam modul in care vom reprezenta problema :

Labirintul va fi reprezentat intr-o matrice L, avand valorile 0 si 1, in care 0 reprezinta 'zid' iar 1 reprezinta 'culoar'. Evident ca ne vom deplasa numai pe culoare, deci succesiunea pe care o vom obtine in final va fi compusa numai din pozitii 'libere'.

Drumul parcurs va fi reprezentat de o stiva implementata printr-o matrice cu doua coloane. Prima coloana va retine indice de linie din matricea L iar coloana a doua va retine indici de coloana ai matricii L. Vom reprezenta stiva printr-un 'tablou cu doua dimensiuni' notat st.

Testul de validitate va fi afirmativ daca pozitia pe care am pus-o pe stiva este libera si negativ in caz contrar.

Pentru a evita situatiile de 'ciclare', in care facem drumuri inainte-inapoi, vom cere, ca o conditie suplimentara de validitate, ca pozitia curenta sa nu fi fost deja vizitata.

Testul de finalitate va fi afirmativ daca pozitia curenta se afla pe frontiera labirintului.

Program labirint

program labirint;

const vecini:array[1..4,1..2] of integer=((-1,0),(0,-1),(1,0),(0,1));

var st:array[0..20,1..2] of integer;

L:array[1..20,1..2] of integer;

a,b,n,m,i,j:integer;

X,Y:INTEGER;

function valid(p :integer):boolean;

var ok:boolean;

k:integer;

begin

valid:=false;

if L[st[p,1],st[p,2]]=1 then

begin

valid:=true;

for k:=0 to p-2 do

if (st[p,1]=st[k,1]) and (st[p,2]=st[k,2]) then

valid:=false;

end;

end;

function final( p:integer):boolean;

begin

final:=false;

if ((st[p,1]=1) or (st[p,1]=n) or (st[p,2]=1) or (st[p,2]=m)) then

final:=true;

end;

procedure tipar(p:integer);

var k:integer;

begin

for k:=0 to p do

writeln(st[k,1],' , ',st[k,2],' ');

writeln;

end;

procedure bktr(p:integer);

var pval:integer;

begin

for pval:=1 to 4 do

begin

st[p,1]:=st[p-1,1]+vecini[pval,1];

st[p,2]:=st[p-1,2]+vecini[pval,2];

if valid(p) then

if final(p) then

tipar(p)

else

bktr(p+1);

end;

end;

begin

writeln('Dati numarul de linii din matrice');

read(n);

writeln('Dati numarul de coloane: m=');

read(m);

for i:=1 to n do

begin

for j:=1 to m do

repeat

writeln('l[',i,',',j,']=');

read(L[i,j]);

until (l[i,j]=1) or (l[i,j]=0);

end;

writeln('LABIRINTUL ARATA ASTFEL:');

for i:=1 to n do

begin

for j:=1 to m do

write(l[i,j]);

writeln;

end;

vecini[1,1]:=0;

vecini[1,2]:=1;

vecini[2,1]:=0;

vecini[2,2]:=-1;

vecini[3,1]:=1;

vecini[3,2]:=0;

vecini[4,1]:=-1;

vecini[4,2]:=0;

writeln('Dati linia de pornire: x=');

read(x) ;

writeln('Dati coloana de pornire: y=');

read(y);

st[0,1]:=x;

st[0,2]:=y;

bktr(1);

end.

Bibliografie

Manual pentru clasa a IX−a, Informatica, varianta Pascal, Tudor Sorin, Editura L&S Infomat, Bucuresti, 2000

Manual pentru clasa a X-a, Informatica, varianta Pascal, Tudor Sorin, Editura L&S Infomat, Bucuresti, 2000

Initiere in Turbo Pascal, Eugenia Kalisy, Irina Athanasiu, Valentin Cristea, editura Teora

Programe Turbo Pascal in Detaliu, Andrei Cioroianu, editura Teora

Manualele scolare, Tudor Sorin, editura Teora

Invatati limbajul Pascal in 12 lectii, editura Teora 2005