REPREZENTAREA GRAFURILOR IN MEMORIA CALCULATORULUI

REPREZENTAREA GRAFURILOR IN MEMORIA CALCULATORULUI

Reprezentarea in memoria calculatorului a grafurilor presupune memorarea numarului de noduri si a legaturilor dintre acestea. In practica cele mai folosite moduri de reprezentare presupun utilizarea variabilelor de tip tablou sau a structurilor de date dinamice.

a)      Reprezentarea grafurilor folosind variabile de tip tablou:

Reprezentarea tata-fii

Se utilizeaza un vector V care pentru oricare nod i ce apartine grafului pastreaza toate nodurile j cu care acesta este adiacent (daca graful este neorientat atunci trebuie respectata conditia j > i, deoarece se repeta muchii ). Prin conventie se separa nodurile tata si adiacentii lor cu valoarea 0.

,0, Nodul i, fiu1i, fiu 2i, fiu 3i,, 0,

Exemplu: Reprezentarea tata -fii a grafului din figura 4.a este:

Fii nodului 2

1, 2, 3, 4, 5, 0, 2, 3, 4, 5, 0, 3, 4, 5, 0, 4, 5, 0, 5, 0

nod tata

2)Liste de adiacenta implementate cu vectori:

In aceasta reprezentare se utilizeaza doi vectori, notati CAP si LEG.

Vectorul Cap va avea dimensiunea n, unde n reprezinta numarul de noduri din graf, si va contine pentru fiecare nod i din graf pozitia din vectorul LEG de unde incep adiacentii nodului i. Separarea nodurilor adiacente cu nodul i de nodurile adiacente cu nodul i+1 se face cu ajutorul valorii 0.

Dimensiunea vectorului LEG depinde de numarul de noduri din graf si de numarul muchiilor garfului si este egal cu n + m (n -numarul de noduri, m - numarul de arce sau muchii).

Exemplu:

Pentru graful din figura 1.3 a) reprezentarea folosind listele de adiacenta implementate cu vectori este de forma:

c). Matricea de adiacenta:

Fie G un graf cu n noduri. Pentru memorarea acestuia in forma numerica se poate folosi o matrice A (n x n) elemente unde

A(i, j)=

Exemplu pentru graful din figura 1.3.a) matricea de adiacenta este:

In cazul grafurilor neorientate matricea de adiacenta este simetrica si deci se va folosi efectiv, doar jumatate din spatiul matricei. De aceea in unele situatii este recomandat ca in cealalta jumatate sa fie memorate alte informatii.

Matricea de adiacenta se va folosi in general pentru grafuri cu numar mic de noduri (aproximativ 250 de noduri).

c).Matricea de incidenta a muchiilor:

Fie un graf cu n noduri si muchii. Pentru memorarea lui se foloseste un tablou bidimensional cu (n x m) elemente unde orice element din matrice poate lua urmatoarele valori:

a(i , j)=

d) Matricea costurilor:

In practica exista situatii cand se cunoaste costul legaturii a doua noduri din graf(exemplu: costul cablului telefonic necesar conectarii a doua posturi telefonice, costul asfaltarii unei portiuni de sosea dintre doua puncte, etc.) si in aceste situatii graful se reprezinta in memoria calculatorului folosind matricea costurilor. Matricea costurilor se noteaza cu C, este o matrice de dimensiune n * n, unde n reprezinta numarul de noduri, iar fiecare element al ei poate lua urmatoarele valori:

C(i, j)=

e) Matricea muchiilor:

Atunci cand sunt cunoscute costurile muchiilor pentru memorarea unui graf se mai poate utiliza si un alt mod de reprezentare interna care foloseste o matrice cu trei linii si un numar de coloane egal cu numarul de muchii (numarul maxim de muchii pentru un graf neorientat este   unde n reprezinta numarul de noduri). O linie din aceasta matrice are forma:

Linia 1: i

Linia 2:  j

Linia 3:  costul muchiei (i , j)

unde:

i, j sunt doua noduri adiacente din graf.

Exemplu: Pentru graful ponderat reprezentat in fig. 1.6 matricea muchiilor este:

M =

Folosind structuri dinamice de date pentru implementarea listelor de adiacenta:

In cazul acestei reprezentari fiecarui nod al grafului i se asociaza o lista de adiacente in care sunt inlantuite toate nodurile cu care acesta este conectat. Acest mod de reprezentare va studiat mai in capitolele urmatoare.

Exemplu: Pentru graful din figura 1.3.a) reprezentarea acestuia prin liste de adiacenta folosind variabile de tip referinta(alocare dinamica a memoriei) este:

Nod Adiacenti

1 Aplicatii rezolvate

Izvoare, rauri, mari.

In tara lui Byte Imparat sunt un numar de n ape curgatoare si mari. Stiind ca intr-un izvor nu se varsa nici o apa, iar marile nu se varsa in alte ape stabiliti:

a)      Care din cele n ape sunt mari si cate sunt

b)      Care sunt izvoare si care sunt.

c)      Care din cele n ape sunt rauri.

d)      pentru un rau k ( k ), stabiliti numarul afluentilor si precizati care sunt.

Datele de intrare se citesc din fisierul text BYTE.TXT de forma:

n - Numarul total de izvoare, rauri si mari

i j mai multe linii de forma i j cu semnificatia ca " i " se varsa in " j "

Exemplu: Daca fisierul text are urmatorul continut:

10

1 4

3 4

2 1

6 5

5 4

8 9

7 8

se va afisa:

Marile sunt:

4 9

Izvoarele sunt:

2 3 6 7 10

Rauri sunt:

5 8

dati apa=5

Are 1 afluent pe 6

Indicatii: Vom considera apele ca fiind nodurile unui graf, iar faptul ca apa i se varsa in apa j va reprezenta muchia (i, j ) a grafului. Se poate observa cu usurinta ca se va obtine un graf orientat (apa curge intr-un singur sens). Se va determina pentru fiecare nod din graf semigradul interior si semigradul exterior.

Vor fi considerate mari acele noduri care au semigradul exterior egal cu zero si semigradul interior diferit de zero.

Vor fi considerate izvoare acele noduri care au semigradul interior egal cu zero si semigradul exterior diferit de zero.

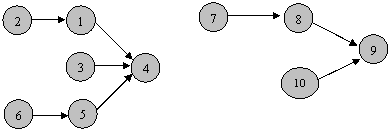Vor fi considerate rauri acele noduri pentru care semigradul exterior si semigradul interior sunt diferite de zero. Pentru fisierul text dat ca exemplu se va obtine urmatorul graf:

Algoritmul de rezolvare scris in limbaj pseudocod este :

Fie graful G cu n noduri si cu muchiile date in fisierul text

mari := Ø

izvor:= Ø

rau:= Ø

pentru fiecare apa i:=1 pana la n executa

sgi := interior(i)

sge := exterior(i)

daca sgi = 0 si sge<>0 atunci

| izvor := izvor + [nodul i]

|_▄

daca sge = 0 si sgi<>0 atunci

| mari := mari + [nodul i]

|_▄

daca sgi <> 0 si sge<>0 atunci

| rau := rau + [nodul i]

|_▄

daca mari + izvor +rau = [1..n] atunci

scrie elementele multimii mari

scrie elementele multimii izvor

scrie elementele multimii rau

citeste apa

daca apa apartine multimii rau atunci

| sgi := interior(i)

| scrie 'numarul afluentilor este', sgi

| scrie afluentii

|_▄

| altfel

scrie date eronate

Se observa ca pentru impartirea nodurilor in mari, izvoare si rauri se pot folosi trei multimi notate cu aceleasi nume. Daca dupa calcularea gradelor si impartirea lor in cele trei multimi reuniunea lor nu este egala cu multimea nodurilor grafului rezulta ca datele de intrare au fost eronate.

2 Probleme propuse

Urmatorul set de exercitii si aplicatii practice pot fi utilizate cu succes in scopul fixarii notiunilor teoretice prezentate anterior precum si al evaluarii cunostintelor elevilor. Ele au grad de dificultate diferit fiind organizate de la simplu la complex, folosind in acelasi timp o serie de cunostinte dobandite anterior (operatii cu vectori si matrice, cunoasterea unui limbaj de programare, prelucrarea fisierelor text care contin date de intrare, folosirea subprogramelor ).

a) Reprezentati figurativ graful memorat cu liste de adiacenta implementate static:

cap: 1 3 6 12 15 19

leg: 3 0 3 6 0 1 2 4 5 6 0 3 5 0 3 4 6 0 2 3 5 0

b)     Scrieti o procedura care primeste ca parametru un nod al grafului si va afisa toti adiacentii acestui nod ( pe baza listelor de adiacenta).

c)     Scrieti matricea de adiacenta asociata acestui graf.

Fie sase firme particulare notate A, B, C, D, E, F care produc diverse piese. Pentru ca o firma sa-si poata desfasura activitatea de productie are nevoie de materiale finite care sunt produse de alte firme dupa cum urmeaza:

Firma A produce piese doar pentru firma F;

Firma B produce piese pentru firmele A, C, D;

Firma C produce piese pentru firmele A, D, F;

Firma D produce piese pentru firmele A, F;

Firma E nu produce piese pentru nici o alta firma;

Firma F produce piese pentru firmele D, E.

Se cere sa se construiasca graful care reprezinta schimburile de piese stabilite intre firmele particulare date.

Indicatie: Se vor considera cele sase firme particulare drept varfurile unui graf, iar relatia de 'schimb' intre diferitele firme va forme muchiile grafului. Se va obtine in final un graf orientat cu sase noduri si unsprezece muchii.

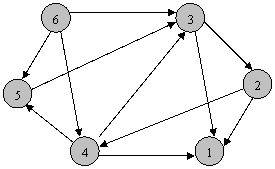
Fie urmatorul graf ponderat:

10

17 100 20

12

a)      Scrieti matricea costurilor pentru acest graf.

b)      Scrieti matricea muchiilor acestui graf

c)      Care sunt gradele interne si externe pentru nodurilor acestui graf

d)      Scrieti o procedura care pe baza matricei de la punctul a) determina nodul cu gradul intern maxim.

e)      Scrieti o procedura care determina transpusul grafului dat.

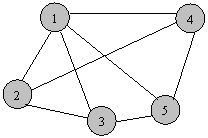Fie urmatorul graf:

a)      Memorati folosind liste de adiacenta (implementate dinamic) graful din figura.

b)      Scrieti o functie care sa calculeze gradul unui nod transmis ca parametru.

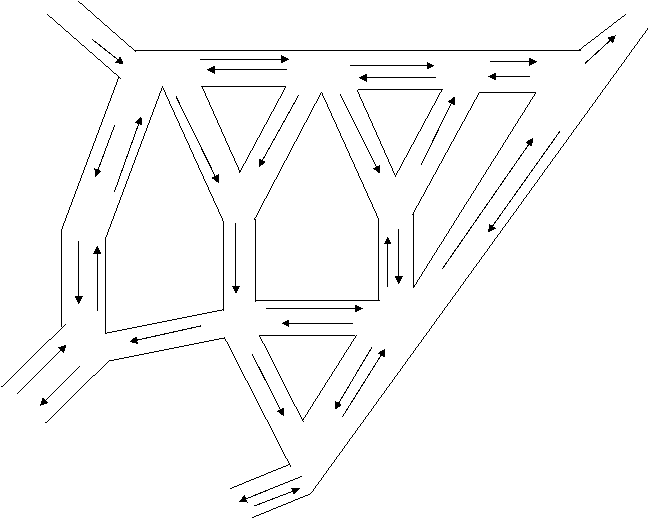
Se considera o retea de strazi ale unui cartier dintr-un oras oarecare. Restrictiile de circulatie in acest cartier sant date in figura urmatoare:

2 12

10 13 14

9 11

8 5

3

7

6

Se cere:

a)      Sa se construiasca graful G corespunzator acestei retele, considerand ca varfurile grafului sant intersectiile strazilor, iar muchia (i, j) exista in graf daca si numai daca un mijloc de circulatie poate sa ajunga de la intersectia i la intersectia j, fara a mai trece prin alta intersectie si bineinteles sa nu fie considerat contravenient;

b)      Scrieti matricea de adiacenta a grafului astfel format;

c)      Scrieti care sunt nodurile adiacente cu varful 1;

d)      Folosind matricea de adiacenta determinati care sunt acele varfuri cu grad exterior de valoare maxima.

Prieteni

Intr-un grup de n persoane se cunosc relatiile de prietenie dintre membrii grupului, care sunt reciproce. Scrieti o procedura care determina persoana cu cei mai multi prieteni si numarul acestora. Verificati apoi daca in grup exista un "morocanos" (adica o persoana care nu este prieten cu nici unul din membrii grupului).

Indicatie

Deoarece relatiile de prietenie sunt reciproce se va obtine un graf neorientat care va avea un numar de noduri egal cu numarul de persoane, iar muchiile grafului vor fi date de relatiile de prietenie dintre membrii grupului.

Pentru a determina persoana cu cei mai multi prieteni este suficient sa se determine care este nodul cu grad maxim (pot fi mai multe noduri care au grad maxim si trebuie afisate toate).

Daca in graful astfel obtinut exista un nod cu grad zero atunci el va fi considerat 'morocanos'.

Sir grafic

Un sir a = (a₁, a₂, ., a_n) se numeste sir grafic daca exista un graf care sa aiba ca grade numerele din acest sir.

Pentru un sir dat cu n elemente numere naturale sa se determine daca acesta este sir grafic.

Indicatii:

Mai intai se ordoneaza descrescator sirul dat. Se va obtine un sir d cu d₁ ³d₂ ³ ³ d_n. Conditiile necesare si suficiente pentru ca sirul d sa fie sir grafic sunt:

d_1£ n si d_n ³

(d₂-1,d₃-1,.,d -1, d , ., d_n ) sa fie sir grafic.

Conditia a doua ne sugereaza si o metoda de rezolvare. Se va elimina din sirul dat nodul cu grad maxim. Dupa fiecare eliminare a nodului de grad maxim , secventa obtinuta conform celei de a doua conditii trebuie ordonata. De aici rezulta complexitatea acestui algoritm este de n * O(sortare) = O(n² log n).

Scrieti un algoritm eficient pentru calcularea transpusului unui graf orientat dat cu n noduri.

a)      graful va fi reprezentat folosind matricea de adiacenta;

b)      graful va fi reprezentat folosind liste de adiacenta (implementate dinamic).

Analizati timpii de executie ai algoritmilor.

Dandu-se doua grafuri (orientate sau nu) sa se determine daca exista o numerotare a varfurilor primului graf astfel incat sa se obtina cel de-al doilea graf. Exemplu de grafuri echivalente:

Soldati (ONI 1993)

Se considera n soldati numerotati de la 1 ..n. Se citesc de la intrare k perechi de numere (i, j) cu i ≠j unde i, j , cu semnificatia ca i este superior lui j. Se cere sa se aseze soldatii intr-un rand, in mod ierarhic, astfel incat fiecare soldat sa aiba toti subalternii sai situati dupa el.

Exemplu:

Pentru n = 6 soldati si k = 4 perechi (1,5),(4,5),(2,3),(1,4) iesirile posibile sunt:

1, 2, 4, 6, 3, 5

6, 2, 1, 4, 5, 3

......

Indicatii:

Consideram cei n soldati ca fiind nodurile unui graf orientat. Intre nodul i si nodul j exista muchia orientata (i, j), daca aceasta muchi apartine perechilor date. Nodul i se numeste predecesorul lui j.

Se elimina succesiv din graf nodurile care nu au predecesori precum si muchiile corespunzatoare. Daca dupa un numar de astfel de eliminari se obtine un subgraf care nu are noduri fara predecesori atunci nu exista solutie, altfel ordinea ierarhica este data de ordinea eliminarii predecesorilor.

Problema acvariului

Intr-un acvariu se afla n pesti carnivori. Stiind care pesti se pot manca unii pe altii se cere sa se determine ordinea in care acestia se mananca intre ei, astfel incat in final sa ramana un numar minim de pesti.

Observatie: Un peste poate fi mancat doar de un peste mai mare decat el.

Restrictii: n<=200

Datele de intrare se citesc dintr-un fisier text avand urmatoarea structura:

pe prima linie este scris numarul de pesti

pe urmatoarele n linii (sub forma unei matrice) sunt scrise relatiile dintre pesti (pe pozitia (i, j) vom avea valoarea 1 daca pestele i poate manca pestele j, 0 in caz contrar)

Exemplu:

Iesirea:

pestele 3 mananca pestele 4

pestele 1 mananca pestele 5

pestele 2 mananca pestele 3

pestele 1 mananca pestele 2

Indicatii:

Reprezentam relatiile dintre pesti sub forma unui graf orientat in care arcul (i, j) are semnificatia ca pestele i poate manca pestele j. Datorita faptului ca un peste mai mic nu poate manca un peste mai mare, graful atasat relatiilor dintre pesti nu va avea cicluri. Ordinea in care se vor manca pestii intre ei va fi determinata astfel:

- la fiecare pas vom gasi un peste care nu poate manca nici un alt peste, dar care poate fi mancat de alti pesti, deci il vom elimina. Acest lucru corespunde cu gasirea unui nod din care nu pleaca nici un arc, dar in care vin arce, si cu eliminarea lui impreuna cu arcele incidente.

Vom repeta pasul de mai sus pana in momentul in care nu mai exista nici un arc in graf.

Cadourile

Trebuie sa determini, pentru un grup de prieteni care-si ofera cadouri unii altora, cu cat da mai mult o persoana decat primeste (sau invers, pentru cei care dau mai mult decat primesc). In aceasta problema, fiecare persoana pune deoparte niste bani pentru cadouri si imparte banii in mod egal pentru fiecare din cei ce vor primi cadouri. Totusi, in anumite grupuri de prieteni, exista oameni care dau mai multi bani decat ceilalti.

Avand dat un grup de prieteni, banii pe care fiecare ii cheltuieste pe cadouri si o alta lista cu prietenii care vor primi cadouri, trebuie sa scrii un program care sa determine pentru fiecare persoana in parte, diferenta dintre cat da si cat primeste.

Intrare:

Fisierul de intrare reprezinta un grup de persoane care dau cadouri si consta din mai multe linii:

Numarul de persoane din grup

O lista cu numele fiecarei persoane din grup

Cate o linie pentru fiecare persoana din grup, care contine: numele persoanei, suma cheltuita pe cadouri, numarul persoanelor care vor primi cadouri de la respectiva persoana, precum si numele acestora. Toate numele se scriu cu litere mici, nu sunt mai mult de 10 persoane intr-un grup si nici un nume nu depaseste 12 caractere. Suma de bani este de tip intreg, pozitiv si strict mai mic decat 2000.

Iesirea:

Numele fiecarei persoane din grup ar trebui sa fie tiparit pe o linie, urmata de castigul (sau pierderea) net, primit (cheltuit) de respectiva persoana. Numele dintr-un grup trebuie sa fie tiparite in ordinea in care apar in fisierul de intrare.

Toate cadourile sunt de tip intreg. Fiecare persoana da aceeasi suma de bani la fiecare prieten si da cat de mult poate. Suma de bani ramasa face parte din suma neta tiparita in fisierul de iesire.

Exemplu:

Pentru fisierul de intrare de forma:

david laura ionut victoria ana

david 200 3 laura ionut victoria

ionut 500 1 david

ana 150 2 victoria ionut

laura 0 2 ana victoria

victoria 0 0

Rezultatul afisat este

david 302

laura 66

ionut -359

victoria 141

ana -150