REPREZENTAREA INFORMATIEI

La nivel LOGIC (abstract)-soft

'0'-zero logic

'1'-unu logic

La nivel(suport)FIZIC-hard

-circuite logice combinationale(porti)

-circuite logice secventiale(bistabili)

BINARY DIGIT=bit='cifra binara'

1 bit b ia valori in si este UNITATEA DE MASURA A cantitatii de INFORMATIE

card=2

COD BINAR =secventa (sir) din una sau mai multe cifre binare adica de biti

b1bo=cod de 2biti care ia valori In multimea variantelor si deci cod=2x2=4

b ₂ b ₁ b₀---> cod de 3biti la care n=2x2x2=8

b7b6b5b4b3b2b1b0-cod pe 8biti (are 256 variante de cod)n=2x2x2x2x2x2x2x2

1 octet=8 biti=1 byte

1 Koctet=2 la puterea 10 octeti=1024 octeti

1Moctet=2 ' ' =1024 Kocteti

SISTEME DE NUMERATIE POZITIONALE :

BINAR, ZECIMAL(Decimal),HEXAZECIMAL(Hexa),OCTAL,

Numerele=CODURI definite pe o multime de b---> simboluri in care b=BAZA SISTEMULUI:

binarydigit---> ; decidigit---> ;

hexa digit-->

POZITIILE IN COD A CIFRELOR se numesc RANGURI: cantitatea Nr exprimata de cifra Cr,de rang r din codul pozitional

Cn-1Cn-2CrC2C1C0 este Nr=b la puterea r =b^r in care,

r--->este RANGUL iar b este BAZA--->

Canitatea totala exprimata prin cod in baza b este un NUMAR Nbaza=Nn-1 + Nn-2 + + Nr ++ N2 + N1 + N0

Se observa ca unei cifre hexa corespund 4 biti,in binar.Aceasta trebuie avut in vedere la conversia unor coduri,cand se scriu relatiile de echivalenta.UN COD BINAR SE DESCOMPUNE IN GRUPURI DE 4 biti (de la dreapta la stanga).

Daca ultimul grup are sub 4 biti se completeaza cu zerouri.Fiecarui grup i se asociaza o cifra hexa.

EXEMPLE

1110101010(B)=35A(H) ; B2A(H)=101100101010(B)

Reprezentarea numerelor in calculatoare

Definitie: Sistemul de numeratie este format din totalitatea regulilor de reprezentare a numerelor cu ajutorul unor simboluri numite cifre.

Sisteme de numeratie: - pozitionale (ex.sistemul zecimal, binar etc.)

- nepozitionale ( ex. sistemul roman )

Un sistem de numeratie pozitional este caracterizat prin baza = reprezinta numarul total de simboluri. Cifrele au o anumita pondere in functie de pozitia lor.

Definitie: Un numar N format din parte intreaga si parte fractionara se poate reprezenta in baza b astfel:

N = xn-1 xn-2..x0. x-1 x-2x-m

pozitia implicita a virgulei

unde o £ xj < b j I n-1, n-2,.., -m

iar valoarea lui N = xn-1 bn-1 + xn-2 bn-2 + .+ x0 + x-1 b-1 ++x-m

n-1

N = å xj bj

-m

Reprezentarea numerelor in calculatoare

Sistemul de numeratie utilizat in calculatoarele numerice este sistemul binar (exista elemente fizice, sigure in functionare care au doua stari stabile). Reprezentarea numerelor in acest sistem prezinta mai multe forme in functie de solutia aleasa pentru rezolvarea celor doua mari probleme:

- pozitia virgulei

- reprezentarea numerelor algebrice ( cu semn )

In functie de pozitia virgulei exista doua reprezentari:

- virgula fixa

- virgula mobila

Virgula fixa.

In calculator se lucreaza cu un numar finit de biti determinat de lungimea cuvintului ( multiplu de lungime de cuvint ). In cazul reprezentarii in virgula fixa , virgula ocupa o pozitie stabilita initial prin proiectare si nu poate fi schimbata. ( Pozitia virgulei este conventionala si nu este realizata fizic ).

( Are importanta pentru structura dispozitivului aritmetic ).

Se pot distinge trei cazuri

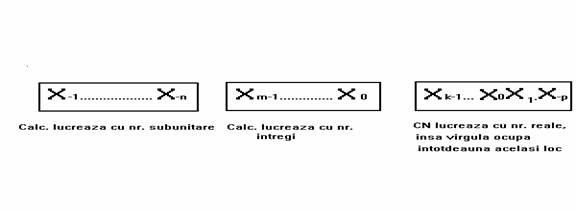
Primele doua reprezentari sunt cele mai utilizate.Reprezentarea in virgula fixa cu numere subunitare prezinta avantajul ca: operatia de inmultire nu duce la depasire.

Virgula mobila.

Numerele reprezentate in virgula mobila vor fi compuse din doua parti mantisa si exponent.

-exponentul - indica ordinul de marime al numarului printr-o putere a lui b

(b= baza de reprezentare a numarului ).

-mantisa - descrie marimea numarului in cadrul ordinului respectiv.

N = M b E unde 1/ b £ M < 1

M- nr. subunitar reprez. in v.f.

E- nr. intreg reprez. in v.f.

Exemplu: in zecimal; 312,56 0.32156 103

312,56 0.032156 104

Numarul de biti alocati pentru mantisa sunt limitati ( fixati de structura hard) asa ca este bine sa incapa cit mai multe cifre semnificative. Pentru aceasta mantisa trebuie normalizata, adica eliminate zerourile de dupa virgula si ajustat exponentul in mod corespunzator.

Reprezentarea numerelor cu semn.

In calculator nu exista posibilitatea de a introduce direct semnele + si -, atasate numerelor pozitive si negative. Aceasta a dus la modalitati speciale de reprezentare a numerelor in calculator, diferite de cele din algebra curenta. Reprezentarea semnului se face cu ajutorul unei cifre binare, denumita cifra de semn si asezata de obicei in prima pozitie.S-a facut conventia ca:

-cifra 0 sa reprezinte numerle pozitive

-cifra 1 sa reprezinte numerele negative

Exista trei forme de reprezentare a numerelor cu semn:

-cod direct ( marime si semn )

-cod invers ( complement fata de 1 )

-cod complementar ( complement fata de doi )

In cazul numerelor in virgula fixa ( subunitare ):

Fie un numar subunitar x = xs x-1.x-m . Sa descriem reprezentarea lui in cele trei coduri:

- cod direct x d = 0. x-1 x-2.x-m pt. x ³ 0

1. x-1 x-2..x-m pt. x £ 0

Are avantajul ca este foarte asemanator cu scrierea naturala, insa din punct de vedere calculatorul prezinta unele dezavantaje legate in special de prelucrari.

- cod invers x i = 0. x-1 x-2..x-m pt. x ³ 0

¾ ¾ ¾

¾ 1. x-1 x-2.x-m pt. x £ 0

x-j = 1- x-j ; j I

- cod complementar x c = 0 x-1 x-2..x-m pt. x ³ 0

1 x-1 x-2 ..x-m pt x < 0

x c = 2 - ½x½

Se observa ca numerele pozitive se reprezinta la fel in toate cele trei coduri.

Pentru numerele negative formele de reprezentare difera, insa exista urmatoarele relatii:

x + x i = x-1 x-m +1 x-1 . x-m =

= 1. 11 ..1 = 2 - 2 -m

x i = 2 - x - 2 -m Þ x c = x i + 2-m

Exemplu: x = 0.011 x i = 1.100

x + x i = 0.011 + 1.100 = 1.111 10000-

1

_________

1.1111

x c = 10000 - 0011

0011

1101

Din aceste relatii rezulta si urmatoarele doua reguli de realizare a complementului fata de doi a unui numar :

1. Se realizeaza complementul fata de 1 si se aduna o unitate la pozitia cea mai putin semnificativa.

2. Se examineaza modulul numarului de la dreapta spre stanga. Zerourile si prima unitate intalnite raman neschimbate. Toate celelalte cifre se neaga.

Formatul de reprezentare a numerelor in calculator FELIX M18

In virgula fixa calculatorul lucreaza pe 8 biti,

Operatii aritmetice binare. Adunarea si scaderea

Adunarea in cod direct

Fie doua numere: x = x s x-1x-m

y = y s y-1y-m

Cazul 1 - x,y au semne diferite:

Regula: Se aduna complementul fata de 1 al modulului celui de-al doilea numar facind adunarea bit cu bit - cu exceptia bitului de semn:

a) Daca apare un transport de la pozitia c.m.s. se aduna 1 la pozitia c.m.p.s. si se da rezultatului semnul primului numar al adunarii ( cel care nu a fost complementat)

b) Daca nu apare un transport de la bitul c.m..s. se ia complementul fata de 1 al rezultatului si se da acestuia semnul celui de-al doilea termen ( cel care a fost complementat )

Exemplu: a) x = 0.101 101 +

011

y = 1.100 1000

x + y i = (0)101 + (0)011 +1

0.001

Exemplu: b) x = 1.010 010 +

010

y = 0.101 100

x + y i = 1.010 + 1.010 = 0.011

Cazul 2 x,y au acelasi semn

Se aduna x + y ( fara bitul de semn ) si se da rezultat semnul comun .

x + y < 1 rezultat corect 0.011 + 0.010 = 0.101

x + y > 1 eroare de depasire 0.100 + 0.101 = 1.101

Scadere - se reduce la operatia de adunare, se neaga bitul de semn al scazatorului si se va efectua adunarea.

Adunarea si scaderea in cod invers

Adunare - Se aduna bit cu bit incepind cu rangul c.m.p.s. inclusiv bitul de semn. Eventualul transport care apare de la bitul de semn se aduna la cifra cea mai putin semnificativa.

x = 0.010 x i = 1101 x i + y i = 11001

y = 0.011 y i = 1100 _______

______ 0010

1001 x + y = 0101

1010

0101

Scadere - Se complementeaza fata de 1 scazatorul si se aduna la descazut dupa regula stabilita anterior.

x = 0101 ; y = 0011 y i = 1100

0101 + 1100 = 10001 = 00010

0101 +

1100

10001

Exemplu 1;

- fie un nr. reprezentat in binar:

x = 1.010 (-2)d [x]i = 0.101 (5)i

y = 1.011 (-3)d [y]i = 0.100 (4)i

[z]i = [x]i + [y]i = 1.001 (1) -> in cod direct 0.110

[z]c = 1.010 <- ( 1.001 + 1 )

[z]d = 1.101

Exemplu 2;

x = 0.0010 [x]i = 1.1101 [x]c = 1.1110

y = 0.0111 [y]i = 1.1000 [y]i = 1.1001

[x + y]d = 0.1001

[x + y]i = 1.0101 + 1 = 1.0110 (i)

[x + y]d = 0.1001

[x + y]c = 1.0111

Adunarea numerelor in virgula mobila ( v fixa )

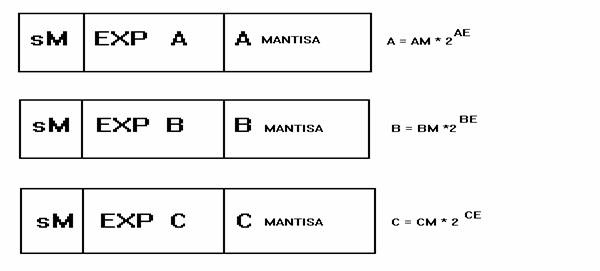
AsAEAM BsBEBM CsCECM

op 1 op2 rezultat

SISTEM INFORMATIC.REPREZENTAREA INFORMATIEI

INTRODUCERE IN INFORMATICA ,anul I ,Fac.A&C

PRELUCRAREA LOGICA A INFORMATIEI BINARE

OPERATII LOGICE ELEMENTARE:NON,AND,OR

Acesti operatori se aplica unor variabile logice x1,x2,in cadrul unor functii logice f(x1,x2,)

Functia f si variabilele x1,x2 iau valori in

-y=NONx=f(x)functia NEGATIE este unara in sensul ca se aplica unei singure variabile x.

in loc de NON se mai foloseste simbolul 'tilda' y=~x sau o bara deasupra lui x astfel .

-AND si OR necesita cel putin 2 variabile logice x1 si x2:

y=(x1)AND(x2)=(x1).(x2)=(x1)&(x2) respectiv

y=(x1)OR(x2)=x1+x2=(x1)|(x2).

Aceste operatii au fost introduse axiomatic de catre John Boolle (sec XVIII) propunand urmatoarele reguli pentru cele trei operatii binare :pt. NON→ ~1=0 ; ~0=1 ;

pt. AND→ 0&0=0 ; 0&1=0 ; 1&0=0 ; 1&1=1 ;

pt. OR--> 0+0=0 ; 0+1=1 ; 1+0=1 ;1+1=1.

Daca notam cu B multimea observam ca variabilele x , x1 , x2 ,iau valori in B.Functia F(x)=~x este F:B→B, iar F(x1,x2),in cazurile AND si OR sunt functii definite pe produsul cartezian B*B si in acest caz F:B*B→B .

Daca functia este de 3 variabile ea este definita pe produsul B*B*B= etc care este o multime cu un nr.de (2x2x2)=8 elemente.In cazul a 4 variabile boolleene avem card(B*B*B*B)=16 etc.

EXEMPLE

F1(x1,x2)=~x1+x2 va putea lua valorile: F(00)=~0+0=1;

F(01)=~0+1=1;

F(10)=~1+0=0+0=0;

F(11)=~1+1=1

TABELUL DE ADEVAR AL FUNCTIILOR LOGICE BINARE

Acest tabel defineste functia.In cazul a n variabile,(x1,x2,,xn),tabelul contine(2 la puterea n)linii si (n+1)coloane din care primele (n)coloane contin produsul ,(B*B*B*B*B) si ultima coloana contine valorile functiei.

EXEMPLE

DIAGRAMELE KARNAUGH ALE FUNCTIILOR LOGICE :

F(x1,X2),F(x1,x2,x3),F(x1,x2,x3,x4)

Diagrama K-h constitue o alta reprezentare a valorilor functiei din tabelul de adevar .Aceasta reprezentare este un dreptunghi in interiorul caruia sunt plasate valorile functiei iar pe cate una din laturile verticale si orizontale sunt scrise valorile celor 'n'variabile ale functiei repective,rezultand tabele diferite in functie de numarul de variabile'n'

CAZUL n=2

In acest caz functia ia 4 valori: F(00),F(01),F(10) si F(11) care sunt plasate in dretunghiul impartit in 4 celule astfel

CAZUL n=3

Valorile functiei in acest caz sunt:F(000),F(001),F(010),F(011),F(100),F(101),F110),F(111).Ele sunt plasate in diagrama astfel:

Atentie!!!

DISTRIBUTIA VALORILOR PE LATURA x2x3 TREBUIE FACUTA ,CA IN FIGURA IN ORDINEA:x2x3→00→01→11→10

CAZUL n=4

In acest caz pe o latura sunt distribuite cele 4 combinatii pentru perechea x1x2 iar pe cealalta latura pentru x3x4 ca in figura urmatoare.

Se obtin astfel 16 celule in care sunt plasate cele 16 valori ale functiei:F(0000),F(0001),,F(1111)

AVANTAJUL REPREZENTARII K-h consta in faptul ca permite aplicarea unei metode ingineresti de proiectare a structurii schemelor circuitelor logice de implementare hard a functiilor logice date prin tabelul de adevar.

REPREZENTAREA MATRICEALA A TABELELOR DE ADEVAR SI DIAGRAMELOR KARNAUGH

Reprezentarea matriceala permite transpunerea pe calculator a unor metode de proiectare logica a circuitelor destinate implementarii hard a unor functii logice date prin tabele de adevar.

PROBLEMA ANALIZEI CLC

Problema analizei este formulata astfel:

- Se da: fie schema logica a CLC-lui de analizat, fie functia logica care-l descrie;

- Se cere: tabelul de adevar al CLC-lui , folosind schema lui ori functia care-l descrie.

Scopul analizei este de a verifica masura in care CLC-ul de analizat raspunde corect la diverse combinatii de valori logice ale variabilelor de intrare.

Daca, spre exemplu, variabilele (marimile) de intrare sunt x₁, x₂, x₃, iar marimea de iesire a CLC-ului este y=f(x₁,x₂,x₃), in care f( ) este cunoscuta se poate calcula se poate calcula raspunsul la diverse combinatii aplicate la intrare: f(000); f(001); f(010); f(011); f(100); f(101); f(110); f(111).

Exemplul 5.1

Se da un CLC descris de functia logica binara numita 'functie majoritate din 3', cu expresia:

Denumirea acestei functii sugereaza comportarea CLC-lui, si anume: raspunsul y=0 cand

majoritatea intrarilor sunt nule, iar cand majoritatea intrarilor sunt unu raspunsul este y=1.

Introducand in expresia de mai sus cele 8 combinatii de valori ale intrarilor rezulta urmatorul tabel:

Tabelul obtinut confirma proprietatile mentionate si analiza arata ca CLC-ul dat prin functia de mai sus este intr-adevar un CLC care prelucreaza logic informatia de vot primita de la un grup de 3 persoane si afisand la iesire rezultatul sub forma y=1 numai daca majoritatea au votat cu '1' si afiseaza y=0 in caz contrar.

PROBLEMA SINTEZEI CLC

Scopul sintezei este obtinerea schemei logice de implementare cu porti elementare(and, non, or) a unui CLC cu determinarea prealabila a expresiei functiei logice care descrie CLC-ul dorit. Cerintele privind CLC-ul dorit sunt exprimate prin intermediul tabelului de adevar.

In consecinta, problema sintezei CLC se formuleaza astfel:

- Se da: tabelul de adevar al unui CLC care trebuie implementat hardware (sau software);

- Se cere: expresia functiei logice a CLC-lui dorit si schema logica a acestuia. 

Pentru rezolvarea acestei probleme, cele mai uzuale metode sunt: metoda directa (bazata pe tabelul de adevar) si metoda Karnaugh (bazata pe diagrame K-h).

Metoda directa de sinteza a unui CLC

Aceasta metoda permite obtinerea unei functii logice y = (x₁,x₂,x₂,,x_n) pe baza tabelului de adevar dat care contine N=2ⁿ linii si reflecta comportamentul dorit al CLC-lui care trebuie construit. Tabelul dat contine m<N linii in care iesirea y=1.

Metoda directa se aplica in 2 pasi:

PASUL 1

Fiecarei linii pe care y=1 i se ataseaza cate un produs al celor n variabile de intrare. Rezulta astfel m produse p₁(x₁x_n), p₂(x₁x_n),,p_m(x₁,,x_n). In aceste produse o variabila intra negata daca pe linia respectiva valoarea ei este nula.

PASUL 2

O functie logica care descrie un CLC al carui tabel de adevar va fi cel dat se obtine prin insumarea celor m produse obtinute la pasul 1:

y=p₁(x₁.x_n)++p_m(x₁x_n)

Trebuie remarcat ca functia obtinuta poate fi simplificata aproape totdeauna pe baza teoremelor algebrei CLC. Aceasta procedura este prea laborioasa pentru a fi folosita in ingineria proiectarii logice a CLC. O metoda inginereasca care furnizeaza o structura optimala este bazata pe diagramele Karnaugh ale CLC-lui care trebuie obtinut. Aceasta metoda furnizeaza o functie cu un numar minim de variabile si de operatii, ceea ce conduce la CLC-ul cel mai ieftin.

Exemplul 5.2

Se da tabelul de adevar din exemplul 5.1. Se cere functia logica aferenta determinata prin metoda directa.

Rezolvare

- Se determina produsele aferente liniilor 8, 7, 6 si 4:

- Se determina functia ca fiind suma produselor:

y = x₁x₂x₃ + x₁x₂(~x₃) + x₁x₂(~x₃) + x₁(~x₂)x₃ + (~x₁)x₂x₃

Constatare:

Se constata ca functia data in exemplul 5.1, pentru acelasi tabel de adevar, este alta mult mai simpla care contine doar: 6 litere, 3 operatori AND, 3 operatori OR.

Astfel, costul implementarii cu CLC-uri (porti) este cel putin dublu in cazul functiei din exemplul 5.2.

Metoda Karnaugh

Algoritmul aplicarii acestei metode implica parcurgerea urmatorilor pasi:

PASUL 1

Pe diagrama Karnaugh data se identifica celulele unitare (care contin 1) si se formeaza din ele grupuri dreptunghiulare de celule unitare adiacente. Baza L si inaltimea h ale dreptunghiului trebuie sa fie puteri ale lui 2:

L=2^a

h=2^b

unde a si b sunt intregi = 0 ,1 ,2,

Numarul de celule din grup este Lxh si deci poate fi numai 1 sau 2 sau 4 sau 8 etc.

Spre exemplu, daca grupul contine o singura celula unitara, a=b=0.

ATENTIE !!

Deoarece in cazul n=3 diagrama Karnaugh este data pe un cilindru, celulele marginale pe generatoare (pe marginile din dreapta si stanga) sunt adiacente, iar in cazul n=4 celulele de pe laturile opuse ale tabelului (diagramei) sunt adiacente deoarece tabelul este pe tor desenat. Aceste aspecte sunt prezentate in cartea: Iacob F., Tertisco A. 'Fundamente ale stiintei sistemelor si calculatoarelor' Editura HYPERION - 1998.

PASUL 2

Fiecarui grup i se ataseaza cate un produs de [n-(a+b)] variabile. De aici rezulta ca pentru optimalitate trebuie formate grupuri de dimensiuni cat mai mari posibil.

PASUL3

Se identifica variabilele din fiecare grup cu regula: daca o variabila nu-si schimba valoarea in lungul (sau in latul) grupului, atunci intra in produsul aferent grupului. Variabila intra negata cand valoarea neschimbata este 0 si invers, intra nenegata cand este 1.

Functia logica care descrie CLC-ul cautat este suma produselor aferente grupurilor.

Exemplul 5.3

Se cere intocmirea diagramei Karnough pentru functia 'majoritate din 3' si prin metoda Karnough descrisa anterior sa se gaseasca structura optimala care implica costul cel mai mic de implementare cu CLC-uri, tinand cont ca pretul implementarii unei porti logice creste in functie de numarul de intrari utilizate ale ei.

Pasul 1

Diagrama Karnough este urmatoarea:

Pe diagrama se pot forma numai 3 grupuri egale caracterizate toate de a+b=1.

Pasul 2

Fiecarui grup i se va asocia cate un produs de cate n-(a+b)=3-1=2 variabile astfel:

Pasul 3

Functia logica cautata va fi:

y = x₁x₂+x₁x₃+x₂x₃

Pe baza acestei functii se poate intocmi schema circuitului de implementare care va necesita 3 porti AND cu cate 2 intrari si o singura poarta OR cu 3 intrari.

SINTEZA UNOR BLOCURI

DE PRELUCRARE A INFORMATIEI

SINTEZA SEMISUMATORULUI DE 1 bit

Semisumatorul (SS) de un bit are ca intrari cei 2 operanzi x, y , iar ca iesiri are tot 2 variabile binare: suma celor 2 intrari x si y, notata SS si respectiv transportul in rangul imediat superior, notat c de la denumirea de 'carry', in engleza. El poate fi realizat hardware printr-un CLC care are urmatorul tabel de adevar:

Acest tabel reprezinta, de fapt, tabla adunarii in binar. Aplicand metoda directa de sinteza, rezulta cele 2 functii logice, SS(x,y) si c(x,y), care descriu CLC-ul de realizare hard a semisumatorului:

SS = ~xy + ~yx implementabila printr-un NOR si respectiv

c = xy implementabila printr-un AND .

Lasam in sarcina cititorului reprezentarea cu simbolurile cunoscute a schemei logice de implementare hardware a circuitului.

SINTEZA SUMATORULUI PE 1 bit

Sumatorul pe un bit are 3 intrari: cei 2 operanzi x, y si respectiv c_i transportul din rangul precedent (indicii folositi sunt i de la INPUT si respectiv o de la OUTPUT). Iesirile sumatorului sunt 2: suma S(x,y,c_i) si respectiv transportul in rangul urmator c_o(x,y,c_i).

Tabelul de adevar al sumatorului pe un bit are 8 linii si 6 coloane:

Acest CLC poate fi realizat cu 2 semisumatoare: primul cu intrarile x, y si iesirile SS₁ = (~x)y + (~y)x, respectiv c₁ = xy, iar al doilea cu intrarile c_i respectiv SS₁ si iesirile SS₂ = (~c_i)(SS₁) + (~SS₁)(c_i), c₂ = c_i SS₁.

Iesirile sumatorului astfel realizat sunt:

S(x,y,c_i) = SS₂ = (~c_i)(~x)y + (~c_i)x(~y) + c_i (x+~y)(~x+y) = (~c_i)(~x)y + (~c_i)x (~y) + c_i (~x)(~y) + c_i xy

c_o(x,y,c_i) = c₁ + c₂ = xy + c_i (~xy + ~yx)

Aplicand metoda directa pe tabelul de mai sus, rezulta aceleasi relatii logice dupa simplificari.

Minimizarea diaframelor Karnough prin introducerea variabilelor in diagramǎ

Fie functia de comutatie de n variabile f_n(x₁,.,x_j-1,x_j,x_j+1,.,x_n).Se poate demonstra prin inductie perfecta urmatoarea egalitate :

f_n(x₁,.,x_j-1,x_j,x_j+1,.,x_n) = x_j f_n-1(x₁,.,x_j-1,1,x_j+1,.,x_n) + (~x_j) f_n-1(x₁,.,x_j-1,0,x_j+1,.,x_n)

Se observa ca cele doua functii f_n-1(x₁,.,x_j-1,1,x_j+1,.,x_n) i f_n-1(x₁,.,x_j-1,0,x_j+1,.,x_n) sunt functii de n - 1 variabile , deci pot fi reprezentate prin doua tabele Karnaugh cu n - 1 variabile.

Fie urmǎtoru exemplu de functie datǎ prin urmǎtoarea diagramǎ Karnough:

Pasii parcusi pentru minimizarea unei functii prin introducerea variabilelor in diagramǎ :

1. Se considerǎ in locul variabilelor introduce " 0 " si se minimizeazǎ.

2. Se considerǎ "1 " in locul unei variabile, celelalte "0" ,unitatiile devin indiferente,

Zerourile rǎmin neschimbate si se minimizeazǎ.

3. Se continuǎ pasii 1 si 2 panǎ se epuizeazǎ toate variabilele introduse.Functia sau intre functiile obtinute la pasii anterior reprezintǎ functia minimǎ rezultatǎ.

1. Sa se construiasca tabela de adevar pentru functia majoritate de 3 variabile.

f majoritate = 1 pt. min 2 intrǎri au val 1.Vezi cursul.

X	y	z	f

2. Sa se minimizeze functiile de comutatie folosind tabelele Karnaugh.

pt. 1 pt. 0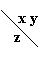

3.

	00	01	11	10
00	0	0	1	1
01	1	1	1	1
11	0	1	0	0
10	0	1	0	0

4.

	00	01	11	10
00	1	0	0	1
01	0	1	0	0
11	0	0	0	0
10	1	0	0	1

5. Sa se minimizeze:

	00	01	11	10
00	1	0	0	1
01	0	-	-	-
11	0	1	-	0
10	0	0	0	0

6.

	00	01	11	10
00	1	-	1	1
01	1	1	1	0
11	0	1	1	1
10	1	1	1	1

7. Se da tabela Karnaugh. Sa se reduca dimensiunea tabelei introducand variabilele x₃, x₄ in tabela si sa se obtina expresiile functiilor:

	00	01	11	10
00	1	1	1	0
01	0	0	1	0
11	0	0	1	1
10	1	1	1	0

Fie functia de comutatie de n variabile f(x₁,x₂, . , x_n). Se poate demonstra prin inductie perfecta urmatoarea egalitate:

f_n(x₁,.,x_j-1,x_j,x_j+1,.,x_n) = x_j f_n-1(x₁,.,x_j-1,1,x_j+1,.,x_n) + (~x_j) f_n-1(x₁,.,x_j-1,0,x_j+1,.,x_n)

	00	01	11	10
0			1	0
1			1

	0	1
0
1		1

1. consideram toate variabilele egale cu zero si exprimam functia cu alipiri de 1.

2.

3.x_{4 = 0}

	0	1			0	1			0	1
0	0	0	+	0	1	0	+	0	0	1
1	0	1		1	1	-		1	0	1

	00	01	11	10
00	0	1	1	0
01	1	0	1	0
11	1	0	0	1
10	1	0	1	0