Sa se interschimbe continutul a doua variabile date

E1.

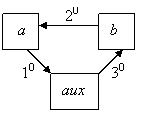Enuntul problemei: Sa se interschimbe continutul a doua variabile date.

Metoda de rezolvare

O prima varianta foloseste o a treia variabila, aux.

Descrierea algoritmului

citeste a,b *se citesc datele de intrare

aux a *in aux se retine temporar valoarea din a

a b *in a punem acum valoarea din b

b aux *in b punem ce depozitasem in aux, adica val din a

scrie a,b *valorile interschimbate (inversate)

O a doua varianta, nu foloseste nicio variabila suplimentara.

Descrierea algoritmului

citeste a,b

a a-b

b a+b

a b-a

scrie a,b

De exemplu, daca se citesc valorile a = 4 si b = 9 se obtine

a a-b => a => a = -5 si b = 9

b a+b => b => a = -5 si b = 4

a b-a => a 4-(-5) => a = 9 si b = 4

Algoritmi cu ramificatii

Definitie: Algoritmii care pot fi descrisi folosind pe langa comenzi/instructiuni de citire (in pseudocod: citeste), scriere (in pseudocod: scrie), atribuire (in pseudocod: ) si comenzi de decizie (in pseudocod: daca-atunci-altfel) sau selectie (in pseudocod: alege) se numesc algoritmi cu ramificatii

Exemplu de algoritmi cu ramificatii

E2.

Enuntul problemei: Sa se calculeze radacinile reale ale ecuatiei ax² + bx + c = 0, unde a, b si c sunt valori reale arbitrare, a nenul.

Metoda de rezolvare: Se foloseste metoda de rezolvarea a ecuatiilor de gradul doi, folosind formulele pentru calculul discriminantului si a radacinilor: Δ = b² - 4ac si
x₁₂ =

Descrierea algoritmului

citeste a,b,c *se citesc datele de intrare

b²-4ac  *se calculeaza discriminantul

*analiza semnului discriminantului

daca < 0 atunci

scrie "Ecuatia nu are radacini reale"

altfel

daca =0 atunci

x1

scrie x1

altfel

x1

x2

scrie x1,x2

E3.

Enuntul problemei: Se considera 3 valori reale retinute in variabilele a, b si c. (i) Sa se determine cea mai mica valoare dintre cele trei valori. (ii) Sa se afiseze cele trei valori in ordine crescatoare.

Descrierea algoritmului

(i) O prima varianta de rezolvare poate fi cea bazata pe compararea valorilor doua cate doua:

citeste a,b,c   *se citesc datele de intrare

daca a≤b atunci

daca a≤c atunci min a  *a≤b si a≤c

altfel min c *c<a≤b

altfel

daca b≤c atunci min b *b<a si b≤c

altfel min c *c<b<a

scrie min *afisarea rezultatului

O alta varianta, mai compacta, si care poate fi usor extinsa la cazul mai multor valori este cea in care se presupune ca valoarea minima este chiar prima, dupa care se compara cu urmatoarele valori, iar in momentul identificarii unei valori mai mici valoarea minima este actualizata.

min = min,c}

citeste a,b,c *se citesc datele de intrare

min a *valorea initiala a minimului se pp. a fi a

daca b<min atunci min b

daca c<min atunci min c

scrie min *afisarea rezultatului

(ii) O prima varianta poate fi aceea in care se identifica toate cele sase variante asociind cate o conditie fiecareia:

citeste a,b,c   *se citesc datele de intrare

daca a<=b si b<=c atunci scrie a,b,c

daca a<=c si c<b atunci scrie a,c,b

daca c<a si a<=b atunci scrie c,a,b

daca c<=b si b<a atunci scrie c,b,a

daca b<a si a<=c atunci scrie b,a,c

daca b<c si c<a atunci scrie b,c,a

O a doua varianta este aceea in care se compara succesive cate doua valori:

citeste a,b,c   *se citesc datele de intrare

daca a≤b atunci

daca b≤c atunci scrie a,b,c

altfel *c<b

daca a≤c atunci scrie a,c,b

altfel scrie c,a,b

altfel *b<a

daca a≤c atunci scrie b,a,c

altfel *c<a

daca b≤c atunci scrie b,c,a

altfel scrie c,b,a

E4.

Enuntul problemei: Sa se citeasca de la tastatura trei numere intregi si sa se stabileasca daca sunt pitagoreice sau nu.

Metoda de rezolvare: Trei numere intregi x, y, z sunt pitagoreice daca verifica teorema lui Pitagora, adica: x² + y² = z² sau y² + z² = x² sau z² + x² = y².

De exemplu:

x =3, y = 4 si z = 5 sunt pitagoreice,

x = 4, y = 3 si z = 5 sunt pitagoreice

x = 1, y = 2 si z = 3 nu sunt pitagoreice

Descrierea algoritmului in pseudocod si C/C++

Pseudocod:

citeste x,y,z

daca x + y² = z² sau y² + z² = x² sau z² + x² = y² atunci

scrie "sunt numere pitagoreice"

altfel

scrie "nu sunt numere pitagoreice"

C:

#include<stdio.h>

#include<conio.h>

void main()

C++:

#include<iostream.h>

void main()

Exercitii efectuate la tabla:

E5. Se introduc varstele a doi copii. Afisati care este mai mare si diferenta de varsta dintre cei doi. De exemplu: pentru 6 si 13 se va afisa 'al doilea copil este mai mare', cu 7 ani

E6. - diferenta dintre doua momente de timp exprimate in ore, min si secunde.

E7. - determinarea mediei generale de admitere a facultate dupa formula media_generala = 50%*medie_bacalaureat + 50%*max.

E8. - Simularea unui calculator de buzunar: se introduc doua numere intregi nenule si o operatie de tipul +, -, *, /, % reprezentand adunarea, scaderea, inmultirea, catul, respectiv restul impartirii primului numar la al doilea; sa se afiseze rezultatul.

Tema (C2) - termen maxim 2 saptamani:

Se citesc trei numere. Sa se verifice daca sunt in progresie aritmetica (a, b, c in progresie aritmetica, daca b = (a+c)/2).

Se introduc trei date de forma numar de ordine pacient, valoare glicemie. Afisati numarul de ordine al pacientilor cu glicemia mai mare decat 100. Exemplu: pentru nr 6 glicemie 90, nr 10 glicemie 107, nr 21 glicemie 110, se va afisa 10 21.

Scrieti in pseudocod (eventual si in C/C++) algoritmul pentru determinarea faptului daca trei numere reale pot forma laturile unui triunghi (adica indeplinesc conditiile a, b, c >0, a+b>c, a+c>b, b+c>a). De exemplu: a=2, b=3, c=2 pot forma laturile unui triunghi, insa a=1, b=2, c=3 nu pot forma laturile unui triunghi pentru ca 1 + 2 3.

Scrieti in pseudocod (eventual si in C/C++) algoritmul pentru determinarea faptului ca trei numere reale formeaza un triunghi isoscel. De exemplu: a=2, b=3, c=2 pot forma laturile unui triunghi isoscel, iar a=2, b=3, c=4 nu pot forma laturile unui triunghi isoscel.