| CATEGORII DOCUMENTE |
| Animale | Arta cultura | Divertisment | Film | Jurnalism | Muzica |
| Pescuit | Pictura | Versuri |
1.Tema proiectului
Sa se estimeze indicatorii de fiabilitate ai setului de date utilizand utilitarul CASRE.
2. Aspecte teoretice ale fiabilitatii software
2.1 Indicatori de fiabilitate
Definitie Fiabilitatea unui program este probabilitatea ca sistemul din care face parte sa opereze fara vreo defectare datorata activarii unui defect in program, in conditii date si intr-un interval de timp dat.
Indicatori:-Fiabilitatea "R(t)" ![]()
-Media timpurilor intre defectari "MTTF" ![]()
-Mediana "m" ![]()
-Rata defectarilor "![]() "
" ![]()
2.2 Modele de fiabilitate
Problema estimarii fiabilitatii software este o problema de predictie, indicatorii prezentati anterior sunt incorporati intr-o forma sau alta in asa numitele modele de fiabilitate software (MFS) acestea sunt modele statistice ce realizeaza predictii asupra ratei de defectare a unui program cunoscandu-se istoria lui. Ele realizeaza si ipoteze asupra procesului de depistare si eliminare a erorilor.
Exista doua tipuri de MFS-uri care prezic timpul intre defectari si care prezic numarul de defectari intr-un interval de timp dat.
Cele dim prima clasa
pot fi exprimate ca o functie densitate de probabilitate ![]() ai carei
parametri pot fi estimati pe baza valorilor timpilor dintre defectele
anterioare, aceasta functie este utilizata pentru a previziona
timpul pana la urmatoarea defectare precum si fiabilitatea
sistemului software. Parametrii lui
ai carei
parametri pot fi estimati pe baza valorilor timpilor dintre defectele
anterioare, aceasta functie este utilizata pentru a previziona
timpul pana la urmatoarea defectare precum si fiabilitatea
sistemului software. Parametrii lui ![]() pot fi
estimati fie prin metoda verosimilitatii maxime fie prin metoda
celor mai mici patrate.
pot fi
estimati fie prin metoda verosimilitatii maxime fie prin metoda
celor mai mici patrate.
In continuare vom prezenta cele mai importante trei modele de estimare a fiabilitatii software:
Modelul Jelinski-Moranda
Ipoteze:
a) Rata detectiei defectelor este proportionala cu numarul curent de defecte din program.
b) Toate defectarile au acela-si probabilitate de aparitie si sunt independente una de alta.
c) Fiecare defectare are acela-si ordin de severitate.
d) Rata de defectare ramane constanta in intervalul dintre doua defectari.
e) Probramul este executat in maniera similara cu functionarea operationala anticipata.
f) Defectele sunt corelate instantaneu fara introducerea in program a unor defecte noi.
g) Numarul total de defecte asteptate este limitat superior.
- predictiile de fiabilitate sunt optimiste.
Modelul Musa-Okumoto
Ipoteze:
a) Detectiile defectarilor sunt independente unele de altele.
b) Numarul de defectari asteptat este o functie de timp logaritmica.
c) Intensitatea de defectare scade exponential cu numarul asteptat al defectarilor aparute.
d) Nu exista o limita superioara a numarului total de defectari.
e) Probramul este executat in maniera similara cu functionarea operationala anticipata.
Principalele caracteristici ale modelului sunt:
- foloseste pentru rata
defectarilor relatia ![]()
- predictia este realizata prin utilizarea unor estimari ale parametrilor.
3. Modelul Littlewood-Verall
Ipoteze:
a) Timpii intre defectari consecutive sunt variabile aleatoare independente fiecare avand o distributie exponentiala.
b) Rata de defectare formeaza o secventa de variabile independente fiecare din ele avand o alta distributie. Cu alte cuvinte programul poate deveni mai putin fiabil pe durata testarii daca in program sunt introduse mai multe defecte decat cele eliminate in etapa de corectie.
c) Nu exista o limitate superioara a numarului de defecte.
Avantaje:
- poate reprezenta incertitudinea depanarii.
- poate reprezenta cresterea sau scaderea fiabilitatii.
Dezavantaje:
nu poate estima numarul defectelor ramase.
Supermodele
Un supermodel se obtine prin combinarea unor modele de baza atribuind fiecaruiea o anumita pondere.
Pot fi definite trei tipuri de combinatii:
Combinatii liniare ponderate statistic
Combinatii in care ponderile sunt atribuite dinamic pe baza comportarii rezultatelor modelelor pe durata celor "n" observatii anterioare.
Combinatii in care ponderile sunt atribuite dinamic pe baza verosimilitatii previzionale asupra celor "n" observatii anterioare.
Testarea datelor
Se poate demonstra ca problema predictiei fiabilitatii unui software are sens numai daca setul de date indica o crestere in timp a fiabilitatii. Astfel exista doua metode care permit detectarea tendintei de evolutie a fiabilitatii inainte de a incepe analiza propriu-zisa a datelor.
Media aritmetica a executiilor
Rezultatele testului sunt afisate grafic si sunt interpretate dupa cum urmeaza.Pentru datele timpi intre defectari daca media executiilor creste atunci timpul intre defectari creste si deci creste si fiabilitatea sistemului, prin urmare modelele pot fi aplicate daca media aritmetica a executiilor este crescatoare.
Testul Laplace
Rezultatele sale sunt ilustrate grafic si sunt interpretate astfel:
se rejecteaza ipoteza nula ca detectia defectelor
urmeaza un proces Poisson omogen , in favoarea unor ipoteze de
crestere a fiabilitatii cu un nivel de semnificatie de "a%"
daca statistica testului este mai mica sau egala cu valoarea la
care functia de distributie cumulativa pentru o distributie
normala este ![]()
se rejecteaza ipoteza
nula ca detectia defectelor urmeaza un proces Poisson omogen
in favoarea unei scaderi de fiabilitate la un nivel de semnificatie
de "a%" daca statistica testului este mai mare sau egala cu valoarea
la care functia de distributie cumulativa pentru
distributia normala este ![]()
se rejecteaza ipoteza
ca exista o variatie a fiabilitatii in favoarea
ipotezei ca nu exista nici o tendinta la un nivel de
semnificatie de "a%" daca statistica testului este intre valorile la
care functia de distributie cumulativa este ![]() si
si ![]()
Vom testa cu ajutorul mediei aritmetice a executiilor si a testului Laplace tendinta pe care o are fiabilitatea odata cu trecerea timpului in cazul setului de date 70.dat.

fig.1 media aritmetica a executiilor
Figura de mai jos (fig.1) reprezinta testul mediei aritmetice a executiilor aplicat setului de date 70.dat si indica o crestere a mediei executiilor ceea ce inseamna o crestere a timpului intre defectari si deci o cerstere a fiabilitatii. Ca urmare modelele pentru predictia fiabilitatii pot fi aplicate cu succes.

fig.2 testul Laplace
Figura
de mai sus reprezinta testul Laplace aplicat setului de date. Se observa ca setul de
valori nu se pastreaza in limitele a ![]() % in jurul valorii medii (4000) deci setul de date este implementabil
pentru dezvoltari ulterioare. In alta ordine de idei observam
ca incepand cu defectiunea numarul 17 cu exceptia a
doua defectiuni toate valorile statistici testului sunt mai mici sau
egale cu -2 ceea ce denota o crestere a fiabilitatii cu un
nivel de semnificatie de 5%, inseamna ca modelele de fiabilitate
pot fi aplicate cu succes pentru acest set de date.
% in jurul valorii medii (4000) deci setul de date este implementabil
pentru dezvoltari ulterioare. In alta ordine de idei observam
ca incepand cu defectiunea numarul 17 cu exceptia a
doua defectiuni toate valorile statistici testului sunt mai mici sau
egale cu -2 ceea ce denota o crestere a fiabilitatii cu un
nivel de semnificatie de 5%, inseamna ca modelele de fiabilitate
pot fi aplicate cu succes pentru acest set de date.
Executia modelelor si interpretarea rezultatelor
Pentru a estima fiabilitatea programului software ale carui caracteristici sunt date prin setul de date, din multitudinea de modele de fiabilitate software existente in utilitarul Casre vom executa doar modelul Musa-Okumoto,modelul Jelinski-Moranda si modelul quadraticLittlewood-Verral considerate ca fiind cele mai importante.
Executia acestor modele impune setarea corespunzatoare a anumitor parametri. Astfel vom considera ca parametrii functiei densitate de probabilitate vor fi estimati prin metoda verosimilitati maxime (maximul likelihood); ca istoric al programului pe baza caruia modele vor realiza predictii asupra ratei de defectare a acestui program vom considera subsetul de date format din prima jumatate a setului de date initial ; numarul de predictii in viitor pe care il vor realiza modelele il vom considera ca fiind 20% din numarul total de defecte (17 defecte). Dupa ce acesti parametrii au fost setati corespunzator putem trece la executia modelelor.

fig.3 timpul intre defectari
In figura de mai sus (fig.3) am reprezentat numarul de defectari in functie de timpul intre defectari. In acesta figura apar pe langa setul de date initial si trei curbe reprezentand predictiile celor trei modele, notate dupa cum apare in legenda din partea de sus a figurii. Reamintim ca prima jumatate a setului de date (defectele nr. 1-67) este folosita ca istoric al programului in timp ce incepand cu a doua jumatate (defectele nr. 68-70) punctele ce formeaza cele trei curbe sunt predictii ale modelelor ce pot fi comparate cu datele reale pentru a vedea daca predictia modelel or se apropie de realitate,ceea ce conform fig.3 este adevarat. Deasemenea punctele care apar dupa cele 3 bare verticale adica dupa defectul 70 reprezinta predictii in viitor ale modelelor prin care se specifica exact cate defectari au mai ramas dupa dupa defectul 70. Analizand fig.3,conform modelului Jelinski-Moranda se observa ca dupa defectul nr.70 nu mai sunt decat 7 defectari. Cu privire la celelalte doua modele acestea estimeza ca dupa defectul cu numarul 70 vor exista mai mult de 20 de defectari. Ceea ce putem spune despre aceste doua modele este ca modelul Musa-Okumoto este mai optimist decat modelul qadratic Littlewood-Verall deoarece modelul Musa-Okumoto estimeza un timp intre defectari mai mare decat timpul intre defectari estimat de modelul qadratic Littlewood-Verall.

fig.4 intensitatea de defectare
In ceea ce priveste intensitatea de defectare reprezentata in figua de mai sus (fig.4) putem spune ca rata de defectare ,conform celor trei modele executate, este paralela cu orizontala ceea ce inseamna ca ea este aproximativ constanta.

fig.5 nr. total de defectari
In figura de mai sus (fig.5) este reprezentat numarul total de defectari in functie de timpul acumulat de la inceputul detectarii defectelor si pana in momentul detectarii celui de-al 162-lea defect (ultimul). Deoarece punctul de start din care modelele isi incep predictia este identic cu primul punct din setul de date cele doua figuri ,nr.total de defectari pentru tot setul de date si nr. total de defectari pentru subsetul de date pentru care s-a aplicat modelele, sunt identice.
Din figura observam ca gra ficul ce reprezinta predictiile modelului Jelinski-Moranda tinde sa devina tangent la asimtota orizontala aflata in dreptul defectarii nr.142, ceea ce inseamna ca numarul total de defectari, conform modelului Jelinski-Moranda, dupa 200.000 secunde este de 142 si ramane constant.Conform modelului Musa-Okumoto dupa 200.000 secunde numarul total al defectelor este de 171 si continua sa creasca odata cu trecerea timpului. Iar in ceea ce priveste modelul qadratic Littlewood-Verall acesta estimeaza ca dupa 200.000 secunde numarul total de defectari este de 195 si continua sa creasca.
Si de aici putem trage concluzia ca modelul modelul qadratic Littlewood-Verall este mai pesimist decat modelul Musa-Okumoto.

fig.6 fiabilitatea
Figura de mai sus (fig.6) reprezinta fiabilitatea pentru urmatoarele 1.864 secunde. Acest interval de timp este setat implicit de utilitarul Casre el fiind intervalul de timp care a tercut de la remedierea penultimei defectari si pana la aparitia ultimei defectari.
Observand (fig.6) modelul Jerinski-Moranda estimeaza ca dupa 200.000 secunde de functionare probabilitatea de buna functionare a programului pentru inca 1.864 secunde este 1. Conform modelului Musa-Okumoto dupa 200.000 secunde de functionare probabilitatea de buna functionare a programului pentru inca 1.864 secunde este 0,67. Iar dupa modelul qadratic Littlewood-Verall dupa 200.000 secunde de functionare probabilitatea de buna functionare a programului pentru inca 1.864 secunde este 0,54.
In ceea ce priveste cresterea de fiabilitate, aceasta se calculeaza ca fiind diferenta dintre fiabilitatea dupa 200.000 secunde (sfasitul predictiei) si fiabilitatea dupa 85.000 secunde (inceputul predictiei in viitor). Astfel modelul Jerinski-Moranda estimeaza o cersretre de fiabilitate de 0,38; modelul Musa-Okumoto prezice o crestere de fiabilitatea de 0,27; iar modelul qadratic Littlewood-Verall presupune o crestere de fiabilitate de 0,18.
Conform celor trei modele executate asupra setului de date exista o crestere de fiabilitate, crestere dealtfel normala deoarece odata cu detectia defectelor ele sunt remediate. Si de aceasta data observam ca modelul Jelinski-Moranda este cel mai optimist in aceasta privinta iar modelul qadratic Littlewood-Verall cel mai pesimist.
Mentionam ca fiabilitatea poate lua valori intre 0 si 1.
In continuare vom prezenta si comenta cele mai importante criterii de evaluare a modelelor de fiabilitate software.
In tabelul de mai jos (fig.7) sunt reprezentate calitatile potrivirii celor trei modele executate asupra setului de date. Acest test se realizeaza in prima faza inaintea aplicarii oricarui alt criteriu de evaluare, scopul testului este de a determina daca rezultatele unui model se incadreaza in nivelul de specificatie specificat. Pentru datele de tip timp intre defectari este folosit testul Komogorov-Smirnov. Pe prima coloana a tabelului avem numele modelului, pe coloana a doua este specificata valoarea calitatii potrivirii (mai exact statistica testului Kormogorov-Smirnov), iar in coloana a treia se indica daca modelul se incadreaza in nivelul de specificatie de 5%. Astfel observam din tabelul de mai jos ca toate rezultatele celor trei modele se incadreaza in nivelul de specificatie de 5% distantele Kolmogorov-Smirnov fiind corecte.
 fig.7 calitatea potrivirii
fig.7 calitatea potrivirii
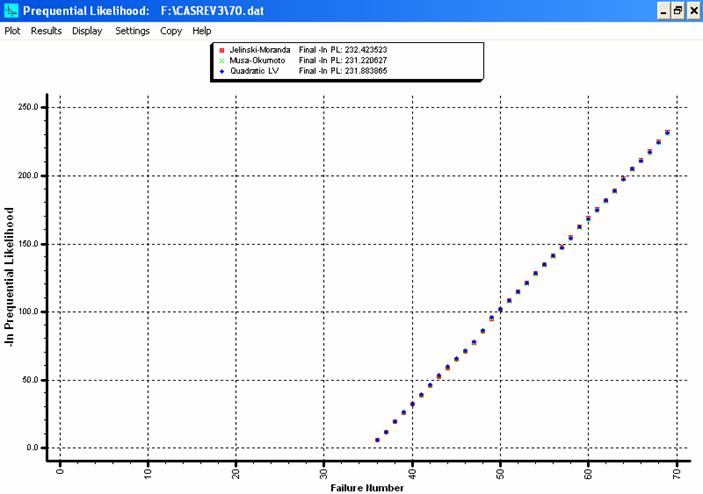
fig.8 verosimilitatea previzionala
In figura de mai sus (fig.8) este reprezentata verosimilitatea previzionala a celor trei modele executate. Acest criteriu de evaluare traseaza grafic rezultatul raportului dintre functiile de verosimilitate a doua modele, insa pentru o reprezentare grafica mai simpla utilitarul Casre afiseaza negativul logaritmului natural al raportului ca functie de numarul de erori incepand cu punctul in care modelele isi incep predictia si pana la sfarsitul predictiei. Acest raport este realizat intre modelul in cauza si un model etalon.
Daca acest raport este unul supraunitar atunci primul model este mai precis decat celalalt; daca raportul este egal cu 1 atunci ambele modele sunt la fel de precise; iar daca raportul este subunitar atunci al doilea model este mai precis decat primul. Pe baza acestor proprietati se poate specifica care dintre cele trei modele are o previziune mai precisa. Legenda din partea de sus a fig.8 ne indica ultimile valori ale negativului logaritmului natural la raportului pentru fiecare model in parte, deci, se observa ca verosimilitatea previzionala a celor trei modele este foarte apropiata una de cealalta.
Precizia relativa prezentat in figua urmatoare (fig.9), care este nu criteriu de evaluare strict legat de verosimilitatea previzionala ilustreza exact probabilitatea ca un model sa fie mai precis decat altele. Observam din (fig.9) ca in intervalul de timp in care modelele proceseaza defectele 67-110 predictia relativa a celor trei modele este aproximativ egala.
In intervalul de timp in care modelele analizeaza defectele 110-130 se observa clar ca modelul cu precizia de estimare cea mai ridicata este modelul qadratic Littlewood-Verall el ajungand sa prezica de apeoape 5.750 de ori mai precis decat modelul Jelinski-Moranda si de aproape 2.000 de ori mai precis decat modelul Musa-Okumoto, in dreptul defectului nr.126. In ultima parte a setului de date, mai precis in dreptul ultimului defect, dupa cum apare si in legenda figurii, modelul Musa-Okumoto ajunge sa prezica de 2.685 de ori mai precis decat modelul Jelinski-Moranda si modelul qadratic Littlewood-Verall ajunge sa prezica de 2.461 de ori mai precis decat modelul Jelinski-Moranda.

fig.9 precizia relativa
Un alt criteriu de evaluare a modelelor de fiabilitate este acela prin care se detrmina tendinta modelului, astfel un model are o anumita tendinta daca estimarile lui se indeparteaza in mod sistematic de comportarea programului deja observata. De exemplu daca un model estimeaza timpi intre defectari mai mari decat cei deja observati putem spune despre modelul respectiv ca are o tendinta optimista. Iar in cazul in care un model estimeaza timpi intre defectari mai mici decat cei deja observati putem spune despre acel model ca are o tendinta pesimista. Acest criteriu de evalure reprezinta graficul unei functii U in functie de numarul de defecte, unde aceasta functie U reprezinta probabilitatea de defectare a programului inainte de timpul Ti estimata de model. Un model care nu are nici o tendinta ar trebui sa aiba un grafic in care toate punctele sa fie distribuite uniform. Modelele care au insa o anumita tendinta prezinta grafice in care punctele apar grupate. Astfel daca aceste puncte sunt grupate in apropierea axei X de-a lungul unui anumit interval de defectari inseamna ca pe acel interval modelul respectiv are o tendinta optimista. Daca insa punctele sunt grupate in partea de sus a graficului de-a lungul unui anumit interval, atunci pe acel interval modelul respectiv va avea o tendinta pesimista.

fig.10 probabilitatea de defectare
Dupa cum observam din figura de mai sus (fig.10) de-a lungul primului interval de defectare (68-100), pentru modelul Jelinski-Moranda avem 20 valori ale functiei U din totalul de 33 sub pragul de 0,5, ceea ce inseamna ca modelul are o tendinta optimista, iar de-a lungul celui de-al doilea interval de defectare (101-70) din totalul de 33 de valori ale functiei U ,27 sunt sub pragul de 0,5 tendinta modelului fiind una puternic optimista.
Modelul Musa-Okumoto de-a lungul primului interval de defectare din totalul de 33 de valori ale functiei U ,22 sunt deasupra pragului de 0,5 modelul avand un caracter pesimist iar de-a lungul celui de-al doilea interval de defectare din totalul de 33 de valori ale functiei U ,20 sunt sub pragul de 0,5 modelul avand un caracter usor optimist. In fine modelul qadratic Littlewood-Verall de-a lungul primului interval de defectare din totalul de 34 de valori ale functiei U ,22 sunt deasupra pragului de 0,5 modelul avand un caracter pesimist, iar de-a lungul celui de-al doilea interval de defectare din totalul de 33 de valori ale functiei U ,18 sunt sub pragul de 0,5 modelul avand un caracter usor optimist
Un alt criteriu de evaluare a modelelor software este graficul U (fig.11) care indica tendinta predictiilor unui model la nivel global fara a tine cont de ordonarea in timp a valorilor distributiilor. In aceasta figura vor aparea distributia cumulativa a functiilor U si distributia cumulativa a probabilitatii reale de defectare, aceasta din urma fiind prima bisectoare. Daca graficul U al unui model este preponderent deasupra primei bisectoare atunci predictia sa pe ansamblul observatiilor este una optimista, iar daca este sub prima bisectoare avem o tendinta pesimista a modelului in cauza. Dupa cum observam din (fig.11) modelul Jelinski-Moranda are tendinta de a face estimatii optimiste in ceea ce priveste timpi intre defectari, in timp ce celelalte doua modele nu au nici un fel de tendinte ele urmarind in deaproape prima bisectoare, aceste presupuneri sunt confirmate si de legenda din partea de sus a figurii, unde ne este indicata valoarea distantei Kormogorov pentru fiecare model si daca ele au o anumita tendinta.
 fig.11
graficul U
fig.11
graficul U
Dupa cum am mai spus graficul U nu arata felul in care
tendinta modelelor s-ar putea schimba in timp. S-ar putea de exemplu ca un
model sa aiba o tendinta pesimista la inceputul
estimarii asuptra setului de date si spre sfarsitul setului de
date acesta sa tinda a fi optimist, acest lucru poate fi ilustrat de
un alt criteriu de evaluare graficul Y prezentat in figura
urmatoare (fig.12).
Interpretarea graficului Y se face la
fel ca si interpretarea

fig.12 graficul Y
Criteriul de evaluare poate cel mai putin folosit este zgomotul modelului (fig.13) , el reprezentand imprecizia proprie a modelului datorata eroorilor introduse de fiecare model prin calculele pe care le executa. Pe masura ce zgomotul modelului creste precizia de estimare a acestuia scade.

fig.13 zgomotul modelelor
In cele din urma modelele pot fi clasificate pe baza a cinci dintre criteriile prezentate mai sus : calitatea potrivirii, verosimilitatea previzionala, graficul U, graficul Y si zgomotul modelului. Aceasta clasificare este de doua tipuri: o clasificare sumara si o clasifcicare detailata. In cadrul primului tip de clasificare modelele vor fi clasificate pe baza celor cinci criterii de evaluare dar tinandu-se cont numai de fiabilitatea masurata pana in momentul inceperii previziunii in viitor a modelelor, pe cand cel de-al doilea tip de clasificare se face tot pe baza celor cinci criterii de evaluare dar tinand cont de toate aspectele nu numai de fiabilitate.
In clasificrea modelelor de fiabilitate aceste cinci criterii prezinta o importanta mai mare sau mai mica in functie de proritatile si ponderile pe care utilizatorul le va atribui acestor criterii. Ponderile atribuite criteriilor pot lua valori intre 0 si 1, cu cat ponderea unui criteriu va fi mai aproape de 1 cu atat el va avea un cuvant mai greu de spus in stabilirea clasamentului modelelor executate. In ceea ce priveste prioritatile acestea au rolul de a stabili ordinea in care vor fi aplicate cele cinci criterii pentru a clasifica modelele executate. Astfel atribuind unui criteriu prioritatea 1 aceasta inseamna ca el va fi primul care va actiona asupra modelelor. Daca el nu poate sa faca diferentierea intre doua modele atunci criteriul cu prioritatea nr. 2 va face acest lucru s.a.m.d. Utilitarul Casre ofera un set implicit de prioritati si ponderi ale celor cinci criterii unde prioritatile sunt urmatoarele:calitatea potrivirii, verosimilitatea previzionala, graficul U, graficul Y si zgomotul modelului iar in ceea ce priceste ponderile acestea au toate valoarea 1.
Observam atat din clasificarea sumara (fig.14) cat si din clasificarea detailata (fig.15) ca modelul cu cele mai precise estimatii este modelul Musa-Okumoto urmat pe locul doi de modelul qadratic Littlewood-Verall si pe locul trei de modelul Jelinski-Moranda.

fig.14 clasificarea sumara a modelelor
Din clasificarea detailata (fig.15) se observa ca modelul qadratic Littlewood-Verall a fost pus pe primul loc de trei dintre criterii, in timp ce modelul Musa-Okumoto a fost clasat pe primul loc doar de doua dintre acestea, modelul Jelinski-Moranda fiind clasat de toate cele cinci criterii pe locul trei. Desi doar doua dintre criteriile de evaluare au clasat modelul Musa-Okumoto pe primul loc acestea fiind cotate cu prioritati si ponderi mai ridicate decat celelalte criterii au propulsat acest model pe primul loc.
Modificand prioritatile si ponderile in limite restranse vom observa ca ordinea celor trei modele nu se schimba, in timp ce daca prioritatile si ponderile se vor modifica in limite largi pe primul loc va trece modelul qadratic Littlewood-Verall, iar pe locul doi modelul Musa-Okumoto, in timp ce modelul Jelinski-Moranda va ramane tot timpul pe locul trei indiferent de modificarile survenite in randul prioritatilor sau a ponderilor. De exemplu modificarea prioritatilor a doua criterii succesive astfel incat ele sa se succeada in ordine inversa sau modificrea oricarei ponderi intr-o plaja de la 0,6 la 1 nu duce la modificarea clasificarii celor trei modele. In schimb de exemplu inversarea prioritatilor criteriilor 2 si 4 sau o atribuire sub 0,6 a unei ponderi duce la modificarea clasamentului.

fig.15 clasificarea detailata a modelelor
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3463
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved