| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
IZOTERME DE ADSORBTIE
In functie de forma lor si de forma buclei de histerezis, izotermele de adsorbtie se clasifica in cinci grupe:
Ø Izoterme de tip I- cunoscute ca izoterme de tip Langmuir; sunt caracteristice adsorbentilor neporosi sau avand micropori cu diametrul sub 25 Å si prezinta urmatoarele particularitati:
- sunt singurele izoterme care se obtin atat sub, cat si peste temperatura critica a adsorbatului;
- descriu atit chemosorbtia cat si adsorbtia fizica;
- valoarea de saturatie a concentratiei superficiale corespunde cu formarea unui monostrat.
Ø Izoterme II si III - sunt caracteristice adsorbantilor macroporosi, cu deosebirea ca izotermele III sunt caracteristice adsorbantilor macroporosi cu interactiuni puternice adsorbant-adsorbat.
Ø Izoterme IV si V- sunt caracteristice adsorbantilor mezoporosi; forma V a izotermelor corespund adsorbantilor mezoporosi cu interactiuni puternice adsorbant-adsorbat.
Prezenta buclei de histerezis este observata la formele IV si V a izotermelor de adsorbtie si uneori la formele II si III.
Tipurile II, III, IV si V se obtin la temperaturi inferioare temperaturii critice a adsorbatului si descriu adsorbtia fizica insotita de formarea unor straturi polimoleculare (izotermele de tip II si III) sau de condensare capilara (izotermele de tip IV si V).
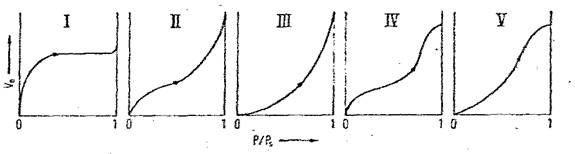
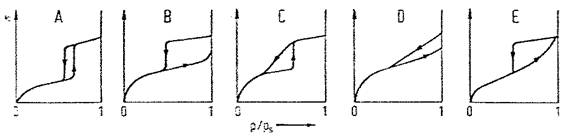
Figura 1. Izoterme de adsorbtie
1. Adsorbtia nedisociativa. Izoterma Langmuir
Cantitatea de gaze (x) adsorbita de un gaz, se exprima prin volumul de gaz, considerat in conditii nprmale, care este retinut prin adsorbtie pe unitatea de masa a solidului si care este functie de presiune, temperatura, de natura adsorbantului si adsorbitului.
x = f (p, T, gaz, solid) (1)
Pentru un anumit sistem adsorbant- adsorbit avem:
x = f (p, T)gaz, solid (2)
Daca adsorbtia se realizeaza la temperatura constanta, atunci:
x = f (p)T, gaz, solid (3)
Aceasta dependenta a adsorbtiei functie de presiunea gazului este descrisa de o izoterma de adsorbtie. Cand se mentine p constant, atunci x variaza functie de T si rezulta o izobara de adosrbtie. In acest caz avem:
f (T)p, gaz, solid (4)
Comparand presiuni la diferite temperaturi si pentru o cantitate de substanta adsorbita, se obtin izostere de adsorbtie, astfel incat:
x = f (T)x, gaz, solid (5)
Cantitatea de gaz adsorbit este invers proportionla cu fractia de suprafata ocupata de moleculele adosrbite, θ.
Procesul este descris de o izoterma de adsorbtie ca cea din figura alaturata, pentru care remarcam un efect de saturare, caracteristic unei anumite valori a presiunii de gaz.
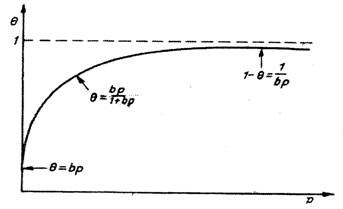
Figura 2. Izoterma de adsorbtie exprimand relatia intre
fractia de suprafata ocupata (θ) si presiunea de gaz (p) pentru adsorbtia nedisociativa
Interpretarea unei astfel de izoterme a fost facuta de Langmuir. Una din izotermele curent utilizate in cataliza eterogena este izoterma lui Langmuir, cunoscuta ca izoterma de adsorbtie in strat ideal.
Ecuatia acestei izoterme este:
θ
=![]() (6)
(6)
in care: θ = fractia de suprafata ocupata prin adsorbtie, considerind suprafata adsorbantului egala cu unitatea
b = coeficient de adsorbtie.
Se presupune ca adsorbtia are loc in conditii ideale:
-suprafata adsorbentului consta dintr-un numar finit de centri de adsorbtie, care nu variaza in timpul desfasurarii fenomenului;
-centrii de adsorbtie sunt echivalenti din punct de vedere energetic si in egala masura accesibili moleculelor adsorbite, adica suprafata este omogena;
-intre corpusculele adsorbite nu se manifesta interactii laterale, de natura sa modifice caracterul si taria legaturilor de adsorbtie.
Exista cateva ipoteze care permit elaborarea unui model simplu pe baza caruia s-a dedus izoterma de tip Langmuir si anume:
Ø adsorbtia are loc numai in strat monomolecular;
Ø intreaga suprafata a catalizatorului are aceeasi activitate pentru adsorbtie (suprafata este omogena, centrii de adsorbtie sunt identici, iar numarul lor este constant);
Ø nu exista interactiuni intre moleculele adsorbite astfel incat cantitatea adsorbita nu are efect asupra vitezei de adsorbtie ,,per centrum'';
Ø procesul este dinamic si pentru conditii date se ajunge la echilibru termodinamic.
In sistemul superficial solid-gaz, moleculele de gaz ataca continuu suprafata si o fractie a acestora pot adera pe suprafata. Datorita energiei cinetice de rotatie si de vibratie, moleculele cele mai incarcate energetic pot parasi continuu suprafata. Se stabileste un echilibru: viteza cu care moleculele ataca suprafata si raman un timp adsorbite poate fi egala cu viteza cu care moleculele parasesc suprafata.
Viteza de adsorbtie este egala cu viteza coliziunilor moleculelor cu suprafata multiplicata cu factorul F, conform relatiei:
ra= rc F (7)
La o temperatura data, numarul de ciocniri poate fi proportional cu presiunea gazului, p si fractia F poate fi constanta.
Astfel, viteza de adsorbtie, ra, pe unitate de suprafata libera poate fi:
fi= rc F = kp (8)
unde: k = constanta de adsorbtie.
rc
= ![]() (9)
(9)
unde: m = masa moleculei;
kB = constanta Boltzmann
Daca fractia de molecule, s, adera la suprafata, ra devine:
ra = ![]() (10)
(10)
Fractia de molecule, s, intotdeauna este mai mica decit 1 deorece:
- pot sa adere numai acele molecule care au energie de activare necesara pentru chemosorbtie;
- pot sa adere numai acele molecule care ciocnesc suprafata neocupata.
Fie: θ = fractia de subprafata ocupata de molecule adsorbite;
1- θ = fractia de suprafata libera;
1 = suprafata totala.
Astfel, fractia de molecule devine:
s = α
(1-θ)![]() (11)
(11)
unde: α = constanta de proportionalitate (coeficient de condensare)
ra = 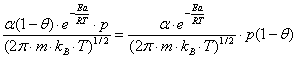 (12)
(12)
ra = kap(1-θ) (13)
unde: ka = constanta de viteza de adsorbtie.
Viteza de desorbtie este proportionala cu fractia de suprafata acoperita:
rd = k' θ (14)
unde: k' = constanta de echilibru de adsorbtie
Se atinge echilibrul de adsorbtie in care viteza de adsorbtie este egala cu viteza de desorbtie:
ra = rd (15)
kap (1-θ) = k' θ (16)
iar ka/k' = Kp = constanta de echilibru de adsorbtie in termeni de presiune
![]() (17)
(17)
![]() (18)
(18)
Relatia (18) reprezinta ecuatia de adsorbtie de tip Langmuir in termeni de presiune.
Sau:
![]() (19)
(19)
unde: v = volumul de gaz adsorbit pentru o anumita fractie de suprafata ocupata, θ
Vm= volumul de gaz chemosorbit pentru intreg stratul monomolecular.
Ecuatia poate fi scrisa si in termeni de concentratie, exprimata in moli adsorbiti pe mol de catalizator.
Fie: c = concentratia adsorbita
cm = concentratia corespunzatoare stratului monomolecular complet de pe catalizator.
Relatia devine:
ra= kCcg(cm-c) (20)
rd= k'cc si Kc= ![]() (21)
(21)
Atunci relatia devine:
ra = rd
![]() =
= ![]() (22)
(22)
Expresia (20) reprezinta izoterma de adsorbtie in termeni de concentratie.
![]() = θ
= θ
Si relatia capata forma:
θ = ![]() (23)
(23)
2. Adsorbtia disociativa
In multe cazuri, adsorbtia este insotita de disociatia moleculelor pe suprafata. S-a constatat experimental, ca adsorbtia hidrogenului se realizeaza, pe metale disociativ, astfel incat fiecare atom de hidrogen ocupa un centru de adsorbtie de pe suprafata. Metanul se adsoarbe pe metale, tot disociativ. In urma adsorbtiei metanului pe filme metalice, s-au dectectat radicali CH3- si CH2- cat si hidrogen atomar adsorbiti pe metal.
In acest caz, adsorbtia o putem considera ca o reactie intre molecula de gaz si doi centrii superficiali adiacenti, iar viteza de adsorbtie va fi:
va = ka p(1-θ)2 (24)
Desorbtia implica reactia intre doi atomi adsorbiti. Viteza de desorbtie va fi proportionala cu patratul fractiei de suprafata ocupata:
vd = kd θ2 (25)
La echilibru va = vd si deci:
 (26)
(26)
Putem scrie aceeasi ecuatie rezolvata in raport cu θ:
![]() (27)
(27)
Fractia de suprafata libera va fi:
![]() (28)
(28)
Din
ecuatia de mai sus se vede ca: daca p
>>1 atunci θ ![]()
daca p >>1 atunci θ ![]()
Se constata ca:
daca p >>1 atunci 1- θ ![]() (29)
(29)
daca p >>1 atunci 1- θ ![]() (30)
(30)
3. Adsorbtia competitiva
Analiza izotermei pentru doua gaze adsorbite pe aceeasi suprafata, se efectueaza presupunand ca fractia de suprafata acoperita de molecula A este θA, iar cea acoperita de molecule B este θB. Fractia libera a suprafetei va fi: 1- θA- θB.
Pentru simplificare, presupunem ca moleculele A si B se adsorb fara
disociatie. Viteza de adsorbtie a componentei A va fi:
vaA = ka pA(1-θA- θB) (31)
unde: pA este presiunea partiala a componentei A.
Viteza de desorbtie a lui A va fi:
vdA = kd θA (32)
La echilibru:
![]() (33)
(33)
unde:
![]()
Un rationament asemanator facut cu componenta B duce la:
![]() (34)
(34)
in care: bB = constanta de echilibru pentru adsorbtia lui B
pB = presiunea partiala a componentei B
Ecuatiile de mai sus sunt doua ecuatii simultane, a caror solutie da fractia de suprafata acoperita de moleculele A si respectiv B.
![]() (35)
(35)
![]() (36)
(36)
Cand pB = 0 sau bB = 0 (B nu este adsorbit), atunci
![]() (37)
(37)
Din ultimele doua ecuatii se constata ca fractia de suprafata, acoperita de un gaz, se micsoreaza cand concentratia celuilalt gaz creste. Se produce in acest caz, o adsorbtie competitiva pe aceiasi centri de adsorbtie, a caror concentratie este limitata.
4. Izoterme experimentale de adsorbtie. Izoterma de adsorbtie B.E.T. (Brunauer-Emmett-Teller)
O corectie adusa modelului Langmuir, consta in realizarea adsorbtiei in multistrat si nu in monostrat. Studiul adsorbtiei fizice permite obtinerea unor informatii privind structura poroasa a catalizatorilor si anume: volumul porilor, forma lor, precum si repartitia porilor dupa dimensiuni, reunite in termenul de textura a catalizatorilor.
Metoda este o teorie aplicata pentru adsorbtia fizica a vaporilor pe solide cu aplicatii in determinarea suprafetei specifice a solidelor. Ecuatia izotermei B.E.T., care descrie adsorbtia in multistrat, are la baza o serie de premise:
Ø Adsorbtia este localizata;
Ø Fiecare centru de adsorbtie retine numai o singura molecula in faza adsorbita;
Ø Adsorbtia are loc cu formarea de straturi polimoleculare;
Ø Fiecare molecula adsorbita in stratul n constituie un centru de adsorbtie pentru
o molecula din stratul n+1;
Ø Suprafata este omogena din punct de vedere energetic;
Ø Incepand cu al doilea strat, caldura de adsorbtie este egala cu caldura de
condensare a gazului.
Reprezentarea grafica a izotermei B.E.T. este redata in figura de mai jos.
In timpul ciclului de adsorbtie, moleculele de adsorbit acopera suprafata pe masura ce presiunea partiala a adostbitului creste.

Figura 3. Reprezentarea grafica a izotermei B.E.T.
S-a demonstrat ca stratul monomolecular adsorbit se realizeaza la valori ale presiunii relative, cuprinse intre 0,05- 0,35. Din determinari de adsorbtie efectuate in acest domeniu, putem calcula volumul de gaz corespunzator pentru realizarea stratului monomolecular adsorbit pe suprafata, Vm.
Tratarea fizica si matematica a acestor ipoteze conduce la urmatoarea ecuatie a izotermei:
![]() (38)
(38)
unde:
p - presiunea de echilibru a adsorbtiei;
p - presiunea de saturatie a adsorbtiei;
Va - volumul de gaz adsorbit la presiunea de echilibru;
Vm - volumul de gaz pentru realizarea monostratului;
p/p - presiune relativa;
C - constanta de adsorbtie dependenta de caldura de adsorbtie qa si caldura de condensare qC prin relatia:
RTlnC = qa- qC (39)
Pentru un anumit sistem adsorbant-adsorbit, Vm si C sunt constante, astfel ca ecuatia B.E.T. devine:
![]() (40)
(40)
unde m si b sunt constante ale caror valori sunt:
 (41)
(41)
Daca reprezentam p / Va(p0 - p) functie de p/p0 obtinem o dreapta a carei panta este m, iar ordonata are valoarea b.
Din punct de vedere calitativ, ecuatia B.E.T. descrie forma izotermei de tipul II. Teoria BET nu considera condensarea capilara, de aceea variatia raportului p / Va(p0 - p) functie de p/p0 este liniara numai pentru substante avand pori cu raze suficient de mari.
In cazul substantelor cu microporozitate cum sunt silicagelul, carbunele activ sau unele sortimente de alumina, simpla aplicare a teoriei BET poate genera erori in evaluarile de suprafete specifice. Pentru a evita aceste erori trebuie sa consideram ecuatia BET sub forma:
 (42)
(42)
in care cu x s-a notat presiunea relativa p/p0, n fiind numarul de straturi adsorbite.
Pentru a calcula Vm , ecuatia de mai sus este folosita in una din cele doua forme limita:
![]() pentru n =1 (43)
pentru n =1 (43)
![]() pentru n = оо (44)
pentru n = оо (44)
Valoarea constantei de adsorbtie C este caracteristica diferitelor tipuri de izoterme experimentale, astfel:
- daca C > 1 rezulta izoterme de tipul III si IV;
- daca C < 1 rezulta izoterme de tipul III si V.
Ecuatia BET sta la baza tehnicilor curente pentru masurarea suprafetei specifice a solidelor. Notiunea de suprafata specifica raportata la gram de solid are semnificatie diferita, dupa cum solidul este neporos sau poros. In primul caz, suprafata specifica este suprafata externa a solidului; in cel de al doilea caz, ea este formata din suprafata externa si cea interna care, in general, este valoric superioara celei dintai si se compune din suprafata totala a porilor.
Cunoscand marimile m si b putem calcula volumul de monostrat si constanta de adsorbtie.
![]() si
si ![]() (45)
(45)
Cunoscand valoarea lui Vm putem determina suprafata probei de solid din relatia:
![]() (46)
(46)
unde: ![]() este volumul molar,
este volumul molar,
![]() este sectiunea
moleculei de gaz adsorbit.
este sectiunea
moleculei de gaz adsorbit.
Valoarea lui ![]() se gaseste in relatia:
se gaseste in relatia:
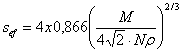 (47)
(47)
M fiind masa moleculara a gazului adsorbit, iar ρ densitatea lichidului adsorbit, la temperatura experientei.
Cand p/p0 ≤ 1 putem utiliza o ecuatie simplificata, similara izotermei Langmuir, anume:
![]() (48)
(48)
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 7646
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved