| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Mecanica punctului material. Tipuri de forte
1. Forte gravitationale
2. Legea atractiei universale
3. Forte de frecare
4. Forte elastice
Forte de legatura
6. Forte de inertie
1. Forte gravitationale
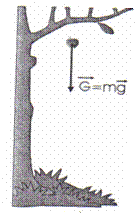
Orice corp ridicat deasupra suprafetei Pamantului cade spre Pamant daca
nu este tinut in aceasta pozitie de o forta. Caderea lui in vid se realizeaza
cu o acceleratie ![]() numita acceleratie gravitationala:
numita acceleratie gravitationala:
![]() (4.1)
(4.1)
Proprietatile fortelor gravitationale:
 Se transmit la distanta prin intermediul
Se transmit la distanta prin intermediul
campului gravitational
Au caracter universal, manifestandu-se intre toate masele de substanta din univers;
Sunt direct proportionale cu masele corpurilor asupra carora actioneaza;
Sunt intotdeauna de atractie;
Fig. 4.1 Caderea corpurilor
datorata fortelor gravitationale
Definitie: Forta cu care un corp apasa normal pe suprafata unui suport orizontal pe care se afla, sau cu care intinde firul de care este suspendat cand firul este vertical se numeste forta de greutate sau simplu greutate.
2. Legea atractiei universale
Evolutia stiintei despre miscarea planetelor
Platon (423 i.e.n - 347 i.e.n) si Ptolemeu (sec. II i.e.n) sustineau ca Pamantul este fix si se afla in centrul sistemului planetar - sistemul geocentric. Nicolaus Copernic (astronom polonez 1473-1543) credea ca
soarele este centrul fix in jurul caruia se misca celelalte planete - sistemul heliocentric. Tycho Brache (astronom danez 1546 - 1601) - fundamenteaza sistemul heliocentric printr-un numar mare de masuratori astronomice. Johannes Kepler (matematician si astronom german 1571 - 1630) stabileste si enunta legile care guverneaza miscarea planetelor in sistemul nostru solar. Sir Isaac Newton (fizician englez 1642-1727) enunta legea atractiei universale.
Legile lui Kepler
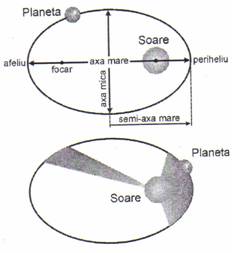 Prima lege a lui Kepler: Orbitele
Prima lege a lui Kepler: Orbitele
(traiectoriile) pe care se misca planetele
sistemului nostru solar sunt elipse;avand
in unul din focare, comun tuturor plane-
telor, soarele.
Legea a doua lui Kepler: Ariile
maturate de raza vectoare (duse de la
soare la planete) in intervale de timp e-
gale, sunt egale.
Fig. 4.2 Miscarea planetelor in Legea a treia a lui Kepler: Patra-
jurul soarelui. tul perioadelor de revolutie a doua planete
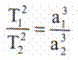 oarecare sunt direct
proportionale cu cuburile semiaxelor mari ale orbitelor eliptice.
oarecare sunt direct
proportionale cu cuburile semiaxelor mari ale orbitelor eliptice.
Legea atractiei universale

(4.3)
Enunt: Oricare doua corpuri materiale punctiforme se atrag cu forte proportionale cu produsul maselor lor si invers proportionale cu patratul distantelor dintre ele.
Constanta de proportionalitate, kg se numeste constanta gravitationala si are valoarea:

(4.4)
Campul gravitational
Definitie: Campul gravitational este spatiul care poseda proprietati speciale, pe care le capata datorita prezentei in anumite puncte ale lui a unor mase de substanta.
Lucrul mecanic al fortelor gravitationale
Consideram o miscare a unui corp de masa m in campul gravitational al unui corp de masa m sub actiunea fortei de atractie gravitationala, pe o distanta considerata suficient de mare astfel incat aceasta nu mai poate fi considerata o constanta, ci depinde inversproportional cu patratul distantei dintre cele doua corpuri.
![]()
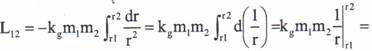 (4.5)
(4.5)
![]()
De unde lucrul mecanic fiind variatia energia potentiala gravitationala:
![]()
Iar energia potentiala gravitationala este:
![]()
3. Forte de frecare
Definitie: Frecarea este fenomenul fizic de aparitie, la contactul dintre doua corpuri solide sau dintre doua straturi adiacente dintr-un lichid, a unei forte care se opune miscarii relative a celor doua corpuri
 sau straturi de fluid. Aceste forte se numesc
sau straturi de fluid. Aceste forte se numesc
forte de frecare.
Fortele de frecare sunt orientate tangen-
tial la suprafata de contact si au sens opus vi-
tezei relative de miscare a celor doua corpuri
sau straturi de fluid.
Clasificarea frecarii:
Frecare externa:
Ø Statica
Ø Cinetica:
Fig. 4.3 Fortele de frecare se ◘ De alunecare
opun miscarii. ◘ De rostogolire
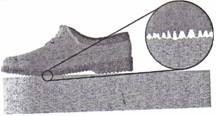
Frecare interna sau frecare de vasco-
zitate.
Forta de frecare care apare la frecarea la alunecare este:
![]()
Fig. 4.4 Fortele de frecare depind
de natura suprafetelor aflate in contact.
unde, a este coeficientul de frecare la alunecare, iar N forta de apasare normala pe suprafata de contact.
Legile frecarii la alunecare:
Forta de frecare nu depinde de marimea suprafetelor de contact dintre cele doua corpuri care se freaca.
Coeficientul de frecare depinde de gradul de slefuire a suprafetelor care se freaca, scazand cu cresterea gradului de slefuire.
Coeficientul de frecare depinde de natura corpurilor care se freaca.
Forta de frecare (statica sau cinetica) este direct proportionala cu forta de apasare la suprafata contactului dintre corpuri.
Frecarea la rostogolire
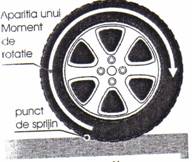
![]()
unde, r este coeficientul de frecare la
rostogolire, r raza de curbura locala a
corpului care se rostogoleste, iar N for-
ta de apasare normala. Forta de frecare
Fig. 4.5 Rostogolirea la rostogolire este mult mai mica decat
forta de frecare la alunecare. In principiu se poate considera ca forta de frecare la rostogolire se datoreaza invingerii unui moment al fortei care apare la o rasturnare a corpului datorita adancirii acestuia in suprafata de contact.
4. Forte elastice
Definitie: Schimbarea dimensiunilor sau formei corpurilor solide sub influenta unor forte aplicat lor se numeste deformare.
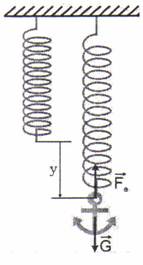
Deformarea poate sa fie:
Elastica - cand dupa incetarea actiunii fortelor exterioare corpul isi revine la forma si volumul initial.
Plastica - cand dupa incetarea actiunii fortelor exterioare corpul nu isi revine sau isi revine numai partial la forma si volumul initial.
![]()
Fig. 4.6 Deformarea unui resort elastic. k este constanta elastica.
![]() Daca consideram o bara cu sectiunea S
asupra careia actioneaza o forta exterioara F atunci se poate defini
efortul unitar ca raportul dintre forta si suprafata:
Daca consideram o bara cu sectiunea S
asupra careia actioneaza o forta exterioara F atunci se poate defini
efortul unitar ca raportul dintre forta si suprafata:
Efectul unui astfel de efort unitar este acela a aparitiei unei alungiri relative a barei considerate:

Constanta de proportionalitate este o constanta de material si se numeste constanta lui Young, E.
![]()
Forta elastica, Fe1 este egala in modul si de sens contrar fortei de deformare exterioare, F:
Lucrul mecanic de deformare elastica

![]()
de unde:

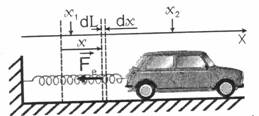 Energia potentiala elastica este:
Energia potentiala elastica este:
![]()
Fig. 4.7 Pentru fortele dependente de
pozitie se considera un interval dx.
Forte de legatura
Definitie:
Fortele care constrang corpurile aflate in miscare sa ur- 
meze o anumita traiectorie se numesc
forte de constrangere sau de legatura
Cel mai celebru exemplu al unor
astfel de forte sunt cele de tensiune ca-
re apar la corpurile suspendate aflate
in miscare.
Fig. 4.8 Transport militar.
6. Forte de inertie
Este momentul sa observam cum arata legile fizicii in sistemele de referinta neinertiale. Legea inertiei nu mai este valabila in sistemele de referinta neinertiale. Se poate demonstra ca legile dinamicii devin din nou valabile daca se accepta existenta unor forte nevazute numite forte de inertie.
Definitie: Forta cu care un corp se opune accelerarii lui se numeste forta de inertie.
Fie date doua sisteme de referinta, dintre care unul fix si celalalt mobil, atunci miscarea unui corp fata de sistemul mobil se numeste miscare relativa. Miscarea corpului fata de sistemul fix se numeste miscare absoluta, iar miscarea sistemului de referinta mobil solidar cu corpul, fata de sistemul de referinta fix se numeste miscare de transport.
![]() Viteza absoluta a unui corp fata de
sistemul de referinta fix,
Viteza absoluta a unui corp fata de
sistemul de referinta fix,![]() este suma dintre viteza acelui corp fata
de sistemul mobil numita viteza relativa,
este suma dintre viteza acelui corp fata
de sistemul mobil numita viteza relativa, ![]() si viteza sistemului mobil fata de cel fix
numita viteza de transport,
si viteza sistemului mobil fata de cel fix
numita viteza de transport, ![]() ,
astfel:
,
astfel:
In general sistemul de referinta mobil poate
executa o miscare de translatie si o miscare de rotatie cu viteza unghiulara![]() .
In acest caz viteza de transport este:
.
In acest caz viteza de transport este:
![]()
unde ![]() este viteza de translatie a SR mobil fata de
SR fix iar
este viteza de translatie a SR mobil fata de
SR fix iar ![]() este viteza tangentiala.
este viteza tangentiala.
Deci viteza absoluta se poate scrie ca:
![]()
Acceleratia absoluta se poate scrie ca:

de unde:
![]()
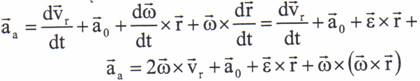
Conform legii a doua a dinamicii:
![]()
![]()
unde:
![]() -forta de inertie la miscarea de
translatie (4.23)
-forta de inertie la miscarea de
translatie (4.23)
![]() -forta
de inertie la miscarea accelerata de rotatie. (4.24)
-forta
de inertie la miscarea accelerata de rotatie. (4.24)
![]() -forta de inertie
centrifuga. (4.25)
-forta de inertie
centrifuga. (4.25)
![]() -forta de inertie
Coriolis. (4.26)
-forta de inertie
Coriolis. (4.26)
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3113
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved