| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Oscilatii fortate. Rezonanta
Sa consideram un oscilator mecanic format dintr-un resort elastic si un corp de dimensiuni neglijabile. Datorita fortei de frecare, energia mecanica a oscilatorului se consuma n timp, astfel ncât oscilatia este amortizata, aa cum am vazut în paragraful 3.4. Pentru a întretine miscarea oscilatorie,trebuie sa se aplice forte exterioare (numite forte de fortare), care sa compenseze pierderile de energie din sistem În acest caz, punctul material va efectua o miscare oscilatorie fortata. Dintre tipurile de forte de fortare (sau perturbatoare) ce se pot aplica sistemului oscilant, un caz interesant pentru aplicatiilepractice este cel n care fortele perturbatoare sunt periodice.
Experienta arata ca o miscare periodica întretinuta prezinta un regim tranzitoriu, dupa trecerea caruia se instaleaza regimul permanent. Regimul tranzitoriu este de scurta durata, iar regimul permanent se manifesta prin oscilatii ntretinute.
1. Rezonanta
Aa cum am vazut n paragraful anterior, dupa stabilirea regimului permanent al oscilatiei întretinute, frecventa de oscilatie este egala cu frecventa fortei perturbatoare. Sistemul oscilant adopta pulsatia fortei perturbatoare, care este diferita de pulsatia sa proprie de oscilatie ca sistem
Rezonanta este fenomenul fizic de aparitie a maximului amplitudinii oscilatiei ntretinute. Sistemul fizic aflat la rezonanta oscileaza cu amplitudine maxima. Deci,din punct de vedere fizic, este ideal sa amplificam la maxim o oscilatie armonica, totusi în practica trebuie evitate situatiile în care frecventa fortei de întretinere coincide cu frecventa proprie a oscilatorului,deoarece în acest caz amplitudinea tinde la infinit. Rezonanta mecanica are multiple aplicatii în tehnica.
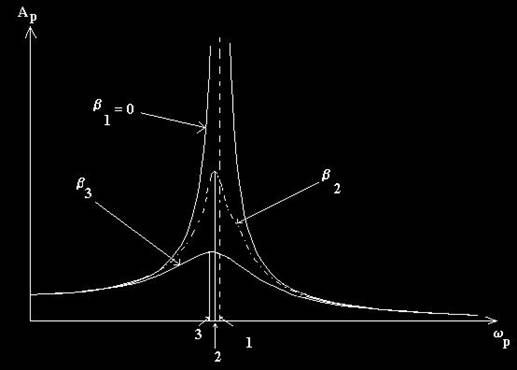
Fig. 3.18. Curbe de rezonanta pentru diferite valori ale coeficientului de amortizare:
Astfel, în acest paragraf am constatat ca în cazul oscilatiilor întretinute, sau fortate, forta exterioara produce un lucru mecanic ce compenseaza pierderile de energie din sistemul oscilant. În paragraful urmator vom vedea cum se caracterizeaza din punct de vedere energetic oscilatiile ntretinute.
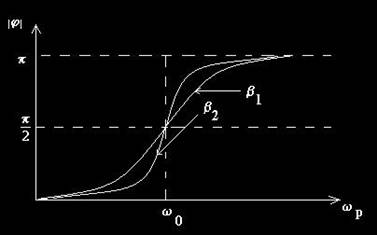
Fig. 3.19. Variatia modulului fazei intiale a oscilatiei permanente în
2. Consideratii energetice ale oscilatiilor fortate
În continuare vom defini câteva marimi fizice care caracterizeaza transferul energiei mecanice în sistemul ce efectueaza oscilatii fortate, sau ntretinute.
1. Puterea instantanee absorbita de sistemul oscilant întretinut reprezinta derivata la timp a lucrului mecanic efectuat de forta de fortare.
2. Puterea medie absorbita în decursul unei perioade reprezinta integrala pe o perioada a puterii instantanee absorbite Pa (t).
3. Puterea instantanee disipata sub forma de caldura de catre forta de frecare reprezinta derivata la timp a lucrului mecanic efectuat de forta de frecare.
4.Puterea medie disipata ntr-o perioada reprezinta integrala pe o perioda a puterii instantanee disipate.
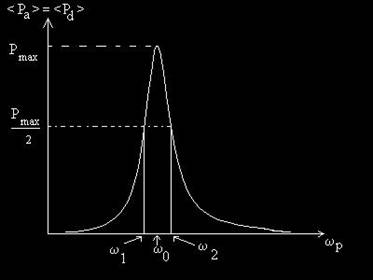
Fig. 3.20. Puterile medii absorbita si disipata
Oscilatii armonice
Un corp efectueaza oscilatii armonice atunci când asupra lui actioneaza o forta de tip elastic:
F = - k x,
k –constanta elastica; x –elongatie; m –masa;
![]() , ω0 – pulsatie proprie;
, ω0 – pulsatie proprie; ![]() , T0 –perioada proprie;
, T0 –perioada proprie;
x(t) = A sin (ω0 t + φ);
Oscilatii amortizate:
Oscilatiile unui corp sunt amortizate atunci cand asupra lui actioneaza, pe lânga forta de tip elastic (- k x) si o forta rezistenta proportionala cu viteza (– α v):
F = - k x – α v, α –coeficient de rezistenta;
![]() ,
,![]() , ω –pulsatia
oscilatiei amortizate;
, ω –pulsatia
oscilatiei amortizate;
β –factor de amortizare;
Observatie: Avem de-a face cu miscare de oscilatie
numai daca ![]() .
.
x(t) = A e - β t sin (ω t + φ);
![]() - decrement
logaritmic;
- decrement
logaritmic;
T – perioada miscarii oscilatorii amortizate.
Oscilatii fortate
Forta care întretine oscilatia este sinusoidala de amplitudine F0 si pulsatie ω1:
F = - k x – α v + F0 sin (ω1 t);
x(t) = A1 sin (ω1 t - φ1 )
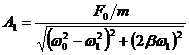
![]() ;
;
A1
(ω1) = maxima ![]() ω1=
ωrez =
ω1=
ωrez =![]() .
.
1.
O particula efectueaza oscilatii
sinusoidale de-a lungul axei Ox în jurul pozitiei de echilibru.
Pulsatia oscilatiilor este ω
= 5 rad/s. La momentul t0=0 particula se
gaseste în pozitia x0
= 12 cm si are viteza ![]() =0,6 m/s.
Determinati legea de miscare si legea vitezei.
=0,6 m/s.
Determinati legea de miscare si legea vitezei.
R: ![]() cm;
cm; ![]() m/s.
m/s.
2. Determinati pulsatia si amplitudinea oscilatiilor sinusoidale efectuate de o particula daca la distantele x1 si x2 de la pozitia de echilibru viteza particulei are valorile v1 si v2.
R: 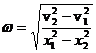 ,
, 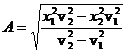 .
.
3. Un corp de masa m = 0,05 kg fixat de capatul unui resort de constanta elastica k = 20 N/m executa o miscare oscilatorie armonica de-a lungul axei Ox. Stiind ca la momentul t0 = 0 corpul are doar energie cinetica, iar energia cinetica maxima a corpului este de 9·10 -3 J, sa se determine:
a) legea de miscare;
b) energia totala a corpului.
R: a) x(t) = 0,03 sin(20 t) m; b) Et = 9·10 -3 J.
4. Un corp de masa m = 0,05 kg fixat de capatul unui resort executa o miscare oscilatorie armonica de-a lungul axei Ox dupa legea:
![]() m. Sa
se determine:
m. Sa
se determine:
a) constanta elastica a resortului si perioada oscilatiilor;
b) energia totala a corpului;
c) momentele de timp la care energia cinetica este egala cu energia potentiala.
R: a) k = 5 N/m, ![]() s; b) Et
= 6.25·10 -3 J; c)
s; b) Et
= 6.25·10 -3 J; c) ![]() s, unde n=numar natural.
s, unde n=numar natural.
5. Un punct material efectueaza o miscare oscilatorie amortizata de-a lungul axei Ox. Perioada miscarii este T=3 s, iar decrementul logaritmic δ=0,6. Sa se scrie legea de miscare, stiind ca la momentul initial t0 = 0, x0 = 0, v0 = 0,5 m/s.
R: ![]() .
.
6. Sa se scrie expresia vitezei oscilatiilor amortizate.
Rezolvare:
x(t) = A0 e - β t sin (ω t + φ),
![]()
![]() ,
,
![]()
![]() ;
;
![]()
![]() ,
,
![]()
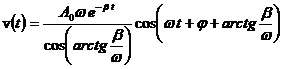
7. Un punct material executa oscilatii amortizate cu pulsatia ω. Sa se determine coeficientul de amortizare β daca la momentul t0 = 0 viteza punctului material este nula, iar elongatia este de n ori mai mica decât amplitudinea.
R: ![]() .
.
8. Un corp oscileaza într-un mediu cu decrementul logaritmic δ1. Care este decrementul logaritmic δ2 daca coeficientul de rezistenta al mediului creste de n ori?
Rezolvare:
![]()
![]()
![]() ;
;
![]()
![]() ,
,
![]()
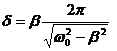
![]()
![]() ;
;
![]()
 ,
,
![]()
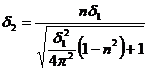 .
.
9. Un corp oscileaza într-un mediu cu decrementul logaritmic δ1. De câte ori trebuie sa creasca rezistenta mediului pentru ca oscilatia amortizata sa devina miscare amortizata aperiodica (β2 = ω0).
R: 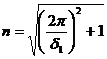 .
.
10.
Un corp de masa m=250 g executa o miscare de
oscilatie amortizata cu factorul de amortizare β = π/4 s – 1, perioada oscilatiilor
proprii fiind ![]() s.
Oscilatiile corpului devin fortate în urma actiunii unei
forte exterioare periodice
s.
Oscilatiile corpului devin fortate în urma actiunii unei
forte exterioare periodice ![]() N. Sa se
scrie elongatia oscilatiilor fortate.
N. Sa se
scrie elongatia oscilatiilor fortate.
R: ![]() m.
m.
11. Amplitudinea oscilatiilor fortate este aceeasi pentru doua frecvente ν1 si ν2. Sa se afle frecventa de rezonanta a oscilatiilor.
R: ![]() .
.
12. Asupra unui corp, care efectueaza o miscare oscilatorie amortizata cu perioada oscilatiilor proprii T0, actioneaza o forta exterioara sinusoidala de amplitudine F0. La rezonanta vitezelor, amplitudinea oscilatiilor este A0. Sa se afle coeficientul de rezistenta.
Rezolvare:
x(t)=A1 sin (ω1 t - φ1 ) - legea de oscilatie în cazul oscilatiilor fortate;
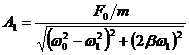
v(t)=A1 ω1 cos (ω1 t - φ1 )
Rezonanta vitezelor se realizeaza atunci când :
ω1 A1= maxima ![]()
![]()
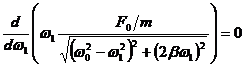
![]() ω1
= ω0
ω1
= ω0
![]()
![]() ;
;
Dar ![]() , iar
, iar ![]()
![]()
![]() .
.
13. Un corp care efectueaza o miscare oscilatorie fortata are amplitudinea vitezei egala cu 1/3 din amplitudinea vitezei la rezonanta vitezelor, pentru doua pulsatii ω1 si ω2. Sa se afle:
a) pulsatia proprie a oscilatorului ω0;
b) factorul de amortizare β.
R: a) ![]() ; b)
; b) ![]() .
.
Compunerea oscilatiilor armonice paralele
a) Oscilatii cu aceeasi pulsatie
x1 (t) = A1 sin (ω t + φ1),
x2 (t) = A2 sin (ω t + φ2);
Rezultatul compunerii a doua oscilatii armonice paralele de aceeasi pulsatie este tot o oscilatie armonica de aceeasi pulsatie pe aceeasi directie.
x (t) = x1 (t) + x2 (t) ![]() x (t) =
A sin (ω t + φ)
x (t) =
A sin (ω t + φ)
![]() ,
, ![]() .
.
b) Oscilatii cu pulsatii putin diferite
Rezultatul compunerii a doua oscilatii armonice paralele de pulsatii diferite nu mai este o oscilatie armonica.
x1 (t) = A sin (ω1 t + φ1),
x2 (t) = A sin (ω2 t + φ2),
x (t) = x1 (t) + x2 (t) ;
Daca pulsatiile sunt foarte apropiate între ele, iar amplitudinile oscilatiilor care se compun sunt egale, oscilatia rezultanta este aproape sinusoidala:
![]()
În cazul
frecventelor acustice sunetul de pulsatie ![]() se aude
succesiv, întarindu-se si slabindu-se cu pulsatia si
perioada batailor:
se aude
succesiv, întarindu-se si slabindu-se cu pulsatia si
perioada batailor: ![]() .
.
Compunerea oscilatiilor armonice perpendiculare
a) Oscilatii cu aceeasi pulsatie
x (t) = A1 sin (ω t + φ1),
y (t) = A2 sin (ω t + φ2);
Traiectoria unui punct material supus simultan la doua
oscilatii armonice perpendiculare de aceeasi pulsatie este o
elipsa a carei forma depinde de ![]() :
:
![]() .
.
b) Oscilatii cu pulsatii diferite
Un punct material supus simultan la doua oscilatii armonice
perpendiculare de pulsatii diferite are o traiectorie complicata.
Daca raportul pulsatiilor este un numar rational
traiectoria este una din figurile Lissajous, forma traiectoriei depinzând
si de diferenta de faza ![]() .
.
14. Un punct material este supus simultan la doua miscari oscilatorii armonice descrise de legile:
x1 (t)
= 1,2 sin ![]() m,
respectiv x2 (t) = 1,6 sin
m,
respectiv x2 (t) = 1,6 sin![]() m.
m.
Sa se scrie legea de miscare rezultanta.
R: x (t) = 2 sin
(![]() t + 0,37 π) m.
t + 0,37 π) m.
15. Un punct material este supus simultan la doua miscari oscilatorii armonice descrise de legile:
a) ![]() m,
m, ![]() m;
m;
b) ![]() m,
m, ![]() m;
m;
c) ![]() m,
m, ![]() m.
m.
Sa se determine ecuatia traiectoriei punctului material, precizându-se forma acesteia.
R: a) ![]() , traiectoria este o dreapta; b)
, traiectoria este o dreapta; b) ![]() , traiectoria este o elipsa având drept axe chiar
axele de coordonate; c)
, traiectoria este o elipsa având drept axe chiar
axele de coordonate; c) ![]() , traiectoria este un cerc.
, traiectoria este un cerc.
16. Sa se determine ecuatia traiectoriei unui punct material supus simultan la doua miscari oscilatorii:
a) x (t) = A sin (ω t), y (t) = A sin (2ω t);
b) x (t) = A sin (ω t), y (t) = A cos (2ω t).
Rezolvare:
a) x = A sin (ω t)![]()
![]()
y = Asin(2ωt) ![]() y = 2A sin
(ω t) cos (ω t),
y = 2A sin
(ω t) cos (ω t),
![]()
![]()
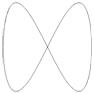
 - traiectoria este una din figurile Lissajous:
- traiectoria este una din figurile Lissajous:
b) Cele doua oscilatii care se compun au acelasi raport al pulsatiilor ca si la punctul a), dar defazajul este altul si deci forma traiectoriei este alta.


|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 383
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved