| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
STRUCTURA DISCONTINUA A RADIATIEI ELECTROMAGNETICE SI ASPECTUL DUAL AL MICROPARTICOLELOR
I. Radiatia termica
Notiuni generale
Corpurile pot emite radiatii sub actiunea a diversi factori. De exemplu: un gaz, sub actiunea unui camp electric intens, emite radiatii, tuburile cu descarcare in neon.
Radiatiile a caror emisie este determinata de incalzirea corpurilor se numesc radiatii termice. In general prin denumirea de radiatie termica se intelege radiatia electromagnetica emisa de corpuri sub actiunea energiei termice. In mod teoretic se poate spune ca orice corp incalzit la T > 0K emite energie sub forma de radiati termice.
Corpurile pot deasemenea sa absoarba radiatia care provine de la mediul exterior si in anumite conditii se poate realiza un echilibru intre procesul de emisie si cel de absorbtie a radiatiilor. cand intre radiatia termica emisa si cea absorbita se stabileste un echilibru se spune ca exista o radiatie termica de echilibru termodinamic.
Cercetarile au aratat ca exista un
spectru continuu pentru radiatia termica, adica domeniul de lungime de unda al
acestor radiatii este cuprins in tot intervalul (0, ![]() ). In cazul echilibrului termodinamic, radiatia termica este
omogena si izotropa.
). In cazul echilibrului termodinamic, radiatia termica este
omogena si izotropa.
Marimi caracteristice radiatiei termice
Pentru a exprima legiile radiatiei termice de echilibru, trebuie sa definim o serie de marimi caracteristice.
a) Fluxul radiant sau energetic (
Repezinta energia emisa de un corp sub forma de radiatii termice, in unitatea de timp, intr-un anumit domeniu spectral.
 (1)
(1)
b) Puterea de emisie sau radianta energetica totala (R)
Puterea de emisie totala a unui izvor de radiatii intr-un punct al sau, este raportul dintre fluxul energetic emis de o suprafata elementara din jurul acelui punct si aria ei normala.
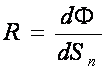 (2)
(2)
c) Puterea spectrala de emisie
Datorita faptului ca nu toate radiatiile, cu frecvente diferite, transporta aceeasi cantitate de energie se defineste o marime numita puterea spectrala de emisie E(ν,T) = reprezinta cantitatea de energie radianta emisa in unitate de timp, intr-un interval de frecveta egal cu unitatea si intr-un unghi solid egal cu unitatea, de catre unitatea de suprafata (aflata la temperatura T) in directie normala.
Conform acestei definitii, energia emisa in intervalul de timp dt si in unghiul solid dΩ, a carui axa face un unghi α cu normala la elementul de suprafata, este:
![]() (3)
(3)
de unde:
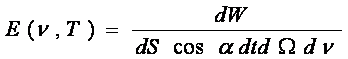 (4)
(4)
d)
Puterea
spectrala de absorbtie ![]() A(ν,T)
A(ν,T)
Puterea spectrala de absorbtie a suprafetei unui corp reprezinta cantitatea de energie radianta incidenta care este absorbita de unitatea de suprafata a corpului considerat, ce se afla la temperatura T intr-un interval de frecventa egal cu unitatea, raportata la energia incidenta :
 (5)
(5)
e) puterea spectrala de reflexie R(ν,T)
In general, corpurile nu absorb in intregime radiatia termica incidenta,o parte din aceasta fiind reflectata. Aceasta reflexie se caracterizeaza printr-o marime spectrala numita putere spectrala de reflexie R(ν,T).

![]() α
α ![]() dS
dS
Legatura dintre puterea spectrala de absorbtie si puterea spectrala de reflexie este data de relatia:
![]() (6)
(6)
f) Densitatea spectrala de energie
Pentru definirea acestei marimi sa consideram o
incinta vidata in care s-a realizat radiatia de echilibru. Viteza radiatiilor
electromagnetice din incinta fiind finita ( ![]() ) densitatea de energie corespunzatoare campului
electromagnetic este data de relatia:
) densitatea de energie corespunzatoare campului
electromagnetic este data de relatia:
 (7)
(7)
![]() ,
, ![]() permitivitatea,
respectiv permiabilitatea vidului, iar E
si H sunt intensitatiile campului electric si magnetic.
permitivitatea,
respectiv permiabilitatea vidului, iar E
si H sunt intensitatiile campului electric si magnetic.
Densitatea spectrala de energie radianta ρ(ν,T) se exprima prin relatia:
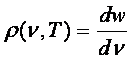 (8)
(8)
Pentru un spectru continuu care cuprinde toate
radiatiile cu frecvente intre 0 si ![]() , densitatea de energie va fi:
, densitatea de energie va fi:
 (9)
(9)
Legea lui Kirchoff. Corp negru
Primele studii asupra proprietatiilor radiatiei termice au fost facute de catre Kirchoff (1859) care stabileste o lege cantitativa.
El arata ca densitatea spectrala de energie ρ(ν,T) nu depinde de natura si proprietatiile incintei in care s-a realizat radiatia termica de echilibru, ci numai de frecventa si temperatura ei.
Pentru radiatia termica de echilibru, cantitatea de energie dintr-un interval de frecvente ν si ν +dν, care cade pe peretii incintei, intr-un anumit interval de timp, este egala cu cea care provine de la acestia, in acelasi interval de timp, adica cu suma dintre energia emisa si cea reflectata de pereti.
Se arata ca:
 (10)
(10)
Aceasta relatie
arata ca raportul dintre puterea spectrala de emisie si puterea spectrala de
absorbtie nu depinde de natura corpului respectiv. Se poate da o semnificatie
fizica functiei ![]() . Din relatia (10) rezulta ca aceasta functie
reprezinta puterea de emisie spectrala a
unui corp a carui putere spectrala de absorbtie este egala cu unitatea, adica
A(ν, T) = 1, atunci E(ν, T) = B(ν, T).
. Din relatia (10) rezulta ca aceasta functie
reprezinta puterea de emisie spectrala a
unui corp a carui putere spectrala de absorbtie este egala cu unitatea, adica
A(ν, T) = 1, atunci E(ν, T) = B(ν, T).
Un sistem material pentru care A(ν, T) = 1 se numeste corp negru ideal. Un corp cu proprietati foarte apropiate de cele ale corpului absolut negru se poate realiza, considerand o incinta cu peretii interiori foarte absorbanti in care se face un orificiu mic S.
O radiatie care patrunde in acest orificiu, sufera un numar foarte mare de reflexii in interiorul incintei, iar probabilitatea ca ea sa paraseasca incinta este foarte mica. Tinand cont ca la fiecare refexie o parte din energia radiatiei este absorbita de peretii cavitatii, aceasta este in mod practic complet absorbita.

S Suprafata S a orificiului se comporta ca un corp absolut negru. Dupa cum rezulta din legea lui Kirchoff un astfel de orificiu va emite de asemenea radiatii care vor avea aceleasi proprietati ca si radiatia emisa de un corp negru aflat la aceiasi temperatura T ca si incinta.
Legea lui Stefan-Boltzman
Experimental, in urma unor masuratori a radiantei totale la diferite corpuri, fizicianul austriac J. Stefan (1879) a stabilit o lege empirica care face legatura intre radianta totala si temperatura. Aceasta a fost demonstrata teoretic, folosind principiile termodinamicii de catre L. Boltzmann (1884). Legea lui Stefan si Boltzmann este exprimata prin relatia:
![]() (11)
(11)
unde R se numeste radianta totala sau puterea de emisie totala, iar σ constatnta lui Stefan-Boltzmann. Determinarile experimentale arata ca valoarea acestei constante este:
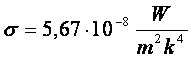
Legile lui Wien
Tot cu ajutorul legilor temodinamicii, Wien stabileste o lege numita legea deplasare (1893).
Experimental se constata ca:
la fiecare temperatura, puterea spectrala de emisie, variaza cu frecventa (respectiv lungimea de unda) si prezinta un maxim pentru o anumita frecventa;
cu cat temperatura corpului creste, pozitia acestui maxim se deplaseaza catre frecvente mai mari, respectiv lungimi de unda mai mici.
Forma curbelor arata ca, culoarea corpului incalzit incepe cu rosu si se
deplaseaza treptat spre violet,pe masura ce temperatura creste.
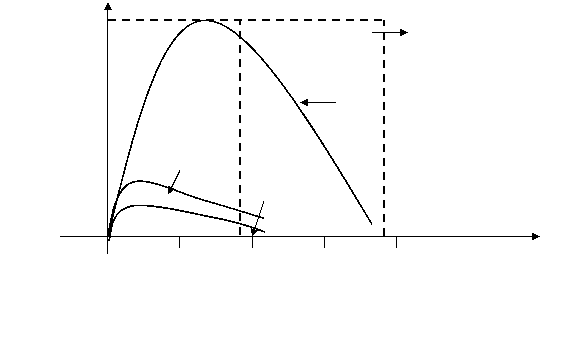 ρ(ν,T) domeniul vizibil T=6000K T=4000K T=2000
ρ(ν,T) domeniul vizibil T=6000K T=4000K T=2000
![]()
0 2 4 6 8
Deoarece puterea spectrala de emisie masoara energia emisa de o suprafata, curbele experimentale arata repartitia energiei in spectrul corpului incalzit.
Wien stabileste ca intre temperatura corpului si lungimea de unda, pentru care puterea de emisie spectrala este maxima, exista urmatoarea relatie:
![]() (12)
(12)
Astfel,
daca corpul are temperatura ![]() el emite spectru
continuu. Pentru radiatia cu lungimea de unda
el emite spectru
continuu. Pentru radiatia cu lungimea de unda ![]() , puterea sa de emisie spectrala are valoare maxima.
Ridicand temperatura corpului la
, puterea sa de emisie spectrala are valoare maxima.
Ridicand temperatura corpului la ![]() ,lungimea de unda variaza,devenind
,lungimea de unda variaza,devenind ![]() astfel incat:
astfel incat:

Asadar cu cat temperatura corpului creste, spectrul sau se deplaseaza catre lungimi de unda mai mici, respectiv frecvente mai mari.
Wien stabileste o lege asupra distributiei spectrale a energiei corpului negru, lege care arata ca densitatea spectrala de energie a corpului negru, la o anumita temperatura este direct proportionala cu puterea a treia a frecventei radiatiei si anume:
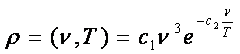 (13)
(13)
Aceasta relatie este verificata pentru frecvente mari, respectiv lungimi de unda mici.
Legea lui Rayleigh-Jeans
Bazandu-se pe teoria clasica a electromagnetismului si a legii clasice de echipartitie a energiei pe gradele de libertate, Rayleigh si Jeans, stabilesc pentru densitatea spectrala de energie relatia:
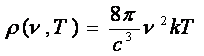 (14)
(14)
Analiza legii Rayleigh-Jeans (14) arata ca ea reproduce corect curbele experimentale, numai pentru frecvente mici, sau λ mari.
In domeniul frecventelor mari, legea Rayleigh-Jeans (14) este complet in dezacord cu rezultatele experimentale.
Legea de distributie a lui Planck
S-a aratat ca legea lui Wien (13) este valabila numai pentru frecventele mari, iar legea lui Rayleigh-Jeans (14) numai pentru frecvente mici, deci fiecare dintre ele este verificabila experimental numai pentru o regiune delimitata a spectrului. Nici una dintre ele nu putea sa explice intregul spectru energetic al corpului negru obtinut experimental.
Max Planck, in 1900
stabileste o lege a radiatiei corpului
negru, care a fost verificata experimental in toate regiunile spectrale. Pentru a ajunge la aceasta lege el
considera ca un corp negru, e format din oscilatori elementari (atomi,molecule, etc.) ce emit radiatia
termica de echilibru in mod discontinuu, cu o energie ce reprezinta un multiplu
intreg al unei valori elementare ![]() , numita cuanta de energie.
, numita cuanta de energie.
Marime ![]() se numeste constanta lui Planck, iar ν repezinta
frecventa proprie a oscilatorului. Astfel energia oscilatorului poate lua numai
valorile:
se numeste constanta lui Planck, iar ν repezinta
frecventa proprie a oscilatorului. Astfel energia oscilatorului poate lua numai
valorile:
(15) ![]()
Pentru deducerea expresiei
densitatii spectrale de energie ![]() , Planck considera ca radiatia termica dintr-o incinta este echivalenta cu
un numar de oscilatori liniari. Se gaseste energia medie a unui oscilator are,
in cazul spectrului energetic discret, expresia:
, Planck considera ca radiatia termica dintr-o incinta este echivalenta cu
un numar de oscilatori liniari. Se gaseste energia medie a unui oscilator are,
in cazul spectrului energetic discret, expresia:
 (16)
(16)
Inmultind (16) cu numarul de oscilatori din unitatea de volum care au frecventa cuprinsa intre ν si ν +dν:
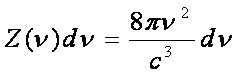 (17)
(17)
obtinem:
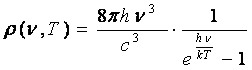 (18)
(18)
Relatia (18) este cunoscuta sub numele de legea de distributie a lui Planck si reprezentarea ei se suprapune perfect peste curba experimentala ce da repartitia de energie, in spectrul corpului negru.
Cazuri particulare a legii de distributie a lui Planck
Din formula radiatiei a lui Planck (18) se pot stabili, pentru anumite conditii, cunoscutele legi ale corpului negru, stabilite initial in urma unor rezultate experimentale.
Astfel calculand densitatea totala de energie se poate regasi legea lui Stefan-Boltzmann
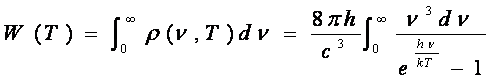
Daca se face notatia:  se obtine:
se obtine:
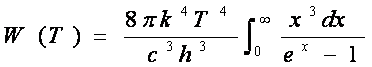
Valoarea integralei este ![]() , deci:
, deci:
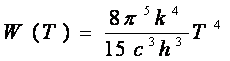 (19)
(19)
Daca se noteaza cu  , relatia (19) devine:
, relatia (19) devine:
(20) ![]() (21)
(21)
Valoarea constantei Stefan-Boltzmann care rezulta din teoria lui Planck este in buna concordanta cu valoarea obtinuta experimental.
Din legea de distributie a lui Planck rezulta si legea de deplasare a lui Wien, conform careia la cresterea temperaturii corpului negru, maximul densitatii spectrale de energie se deplaseaza spre domeniul valorilor mici ale lungimilor de unda.
Pentru a obtine aceasta lege se exprima densitatea spectrala de energie functie de lungimea de unda, adica:
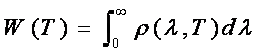 (22)
(22)
si facand inlocuirea 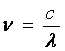 avem:
avem:
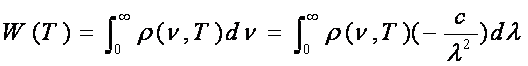
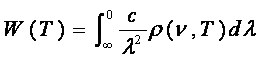 (23)
(23)
Din relatiile (22) si (23) avem:
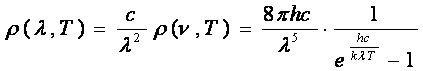
Introducand notatia 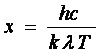 si impunand conditia
de maxim pentru functia
si impunand conditia
de maxim pentru functia ![]() , adica
, adica  rezulta
urmatoarea ecuatie:
rezulta
urmatoarea ecuatie:
![]()
Solutia acestei ecuatii, care trebuie rezolvata grafic sau numeric este:

de unde rezulta legea de deplasare a lui Wien:
(24)![]()
unde:
(25)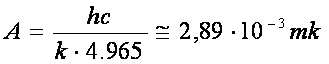
de asemenea valoarea acestei constante dedusa cu relatia (25)este in buna
concordanta cu cea dedusa pe cale experimentala. In cazul frecventelor mici,
adica ![]() , atunci:
, atunci:
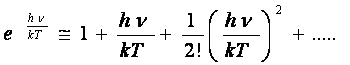
si atunci relatia (18) devine:

ceea ce exprima legea lui Rayleigh-Jeans valabila pentru domeniul spectral cu ν mici, deci cu λ mari.
Daca ![]() , atunci:
, atunci:
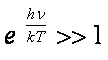
si deci la numitorul relatiei (18) se poate neglija 1. Astfel se obtine legea semiempirica a lui Wien:
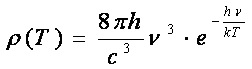
Aplicatii ale legilor radiatiei termice
Cu ajutorul legilor radiatiei termice se poate determina temperatura cu ajutorul unui corp negru, sau a unui corp avand proprietati asemanatoare cu acesta.
Metodele de determinare a temperaturii prin aceste legi se numesc metode de pirometrie optica.
Pentru ca o sursa de
radiatie luminoasa sa fie economica trebuie ca maximul energiei emise sa cada
in domeniul vizibil. Din legea de deplasare a lui Wien, tinand cont ca
temperatura filamentului unei lampi cu incandescenta nu poate depasi 3000 K,
rezulta ca lungimea de unda corespunzatoare maximului densitatii de
energie este: ![]() , adica λ din domeniul infrarosu al spectrului. Aceasta
arata ca sursele care se bazeaza pe incadescenta unor corpuri sunt foarte
neeconomice. Pentru a fi economice , temperatura de incadescenta ar trebui sa
fie mai mare sau cel putin egala cu 5000K, dar o astfel de sursa cu
incandescenta nu se poate realiza.
, adica λ din domeniul infrarosu al spectrului. Aceasta
arata ca sursele care se bazeaza pe incadescenta unor corpuri sunt foarte
neeconomice. Pentru a fi economice , temperatura de incadescenta ar trebui sa
fie mai mare sau cel putin egala cu 5000K, dar o astfel de sursa cu
incandescenta nu se poate realiza.
Sursele de lumina cu incadescenta sunt din ce in ce mai mult inlocuite cu lampile cu fluorescenta.
Acestea sunt mult mai economice, dau un spectru comparabil cu al soarelui si au randamentul de doua ori mai mare decat lampile cu incandescenta.
II. Natura corpusculara a radiatiei
Se vor studia fenomenele ce necesita introducerea structurii discontinue a radiatiei electromagnetice.
Efect fotoelectric
Printre fenomenele in care se manifesta actiunea luminii asupra substantei, un loc important il ocupa efectul fotoelectric. El a fost descoperit de Hertz in 1887, care a observat ca, iluminand cu radiatiile ultraviolete electrozii intre care se produce o descarcare electrica in scantei, aceasta se produce mai rapid.
Efectul fotoelectric consta in emisia de electroni de catre un metal, pe suprafata caruia cade un flux de radiatii electromagentice de frecventa inalta.
Interpretarea teoretica corecta a acestui efect a fost facuta de Einstein pe baza teoriei fotonice asupra luminii.
Pentru studiul efectului fotoelectric este folosit un dispozitiv numit celula fotoelectrica, alcatuita din doi electrozi introdusi intr-un tub vidat. Catodul este construit din metalul la care se studiaza emisia de electroni sub actiunea luminii.
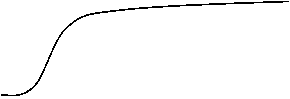
Iluminand catodul si aplicand o diferenta de potential intre catod si anod, electronii emisi de catod ajung la anod, determinand un curent electric numit curent fotoelectric. Pentru o diferenta de potential suficient de mare, toti electronii emisi de catod, ajung la anod, dand un curent de saturatie, a carui valoare este cu atat mai mare cu cat fluxul luminos este mai mare.
![]() I
I

![]()
![]()
![]()
![]()
![]()
U
In urma unor cercetari experimentale au fost stabilite urmatoarele legi ale efectului fotoelectric:
intensitatea curentului de saturatie, determinata de numarul de electroni smulsi din fotocatod in unitatea de timp, este proportionala cu fluxul incident.
energia cinetica maxima a fotoelectronilor este proportionala cu frecventa radiatiei incidente si nu depinde de intensitatea acesteia.
efectul fotoelectric se produce numai
pentru frecvente care sunt mai mari decat o frecventa de prag ![]() ;
;
efectul fotoelectric se produce intr-un interval de timp foarte scurt, practic instantaneu.
Durata de la caderea radiatiei si pana la procesul de emisie fiind
aproximativ ![]() s.
s.
Pe baza naturii ondulatorii a luminii nu s-au putut explica aceste legi experimentale.
Daca se admite ca energia transportata de lumina este distribuita uniform fiecarui electron, atunci energia fotoelectronului ar trebui sa creasca la marirea intensitatii fascicolului incident, contrazicand legea a doua.
Conform teoriei ondulatorii, efectul fotoelectric ar trebui sa se produca pentru orice frecventa, daca intensitatea luminoasa este mare, ceea ce nu poate explica existenta frecventei de prag.
Astfel oricat de mica ar fi frecventa radiatiei, la o intensitate suficient de mare, electronul ar primi o energie suficienta pentru a parasi metalul. Aceasta energie este caracteristica pentru fiecare substanta si se numeste energie de extractie, corespunzator lucrului mecanic de extractie.
Nu s-a putut explica de asemenea lipsa inertiei in emisia fotoelectronilor pe baza teoriei ondulatorii a luminii. Ar rezulta ca un fascicol incident de intensitate mica, actionand in timp ar ceda electronilor energia corespunzatoare lucrului mecanic de extractie si acestia ar parasi metalul dupa un timp lung, fapt infirmat de experienta.
Einstein a aratat ca legile efectului fotoelectric pot fi explicate numai pe baza unei noi teorii asupra luminii. Extinde teoria lui Planck privind structura dicontinua a radiatiilor. Einstein presupune ca radiatia luminoasa este concentrata in cantitati finite de energie, de marime hν, in corpusculi de energie luminoasa, numiti fotoni. In aceasta teorie fotonica, intensitatea fluxului de lumina incident este direct proportionala cu numarul de fotoni. Daca N este numarul de fotoni ce trece in unitatea de timp prin unitatea de suprafata normala la directia de propagare a fascicolului, atunci:
(26)![]()
Daca intensitatea radiatiei electromagnetice creste atunci, numarul de fotoni se mareste corespunzator, dar energia fiecarui foton ramane aceeasi, atata timp cat frecventa este constanta.
Einstein considera ca energia fotonului incident, absorbita integral de catre electron, este folosita pentru parasirea metalului efectuandu-se lucrul mecanic de extractie, iar restul este transformata in energie cinetica a fotoelectronului. Bilantul energetic conduce la relatia lui Einstein pentru efect fotoelectric de forma:
(27)![]()
unde ![]() este energia cinetica maxima a fotoelectronului in cazul
in cand
este energia cinetica maxima a fotoelectronului in cazul
in cand ![]() reprezinta
lucrul de extractie a unui electron de pe suprafata metalului. Pentru
electronii aflati pe straturile inferioare in metal, lucrul mecanic de
extractie este mai mare si deci energia lor cinetica este mai mica.
reprezinta
lucrul de extractie a unui electron de pe suprafata metalului. Pentru
electronii aflati pe straturile inferioare in metal, lucrul mecanic de
extractie este mai mare si deci energia lor cinetica este mai mica.
Lucrul mecanic de extractie
depinde, evident de natura metalului folosit; astfel metalele alcaline au un
lucru mecanic de extractie mic,
frecventa de prag situandu-se in domeniul
vizibil spectrului, dar majoritatea metalelor au un ![]() ridicat cu
ridicat cu ![]() in ultraviolet.
in ultraviolet.
Radiatia Rntgen
Descoperita in 1895 de catre Rntgen si denumita "X" deoarece initial nu se cunostea originea ei. Aceasta radiatie a fost produsa in urma ciocnirii electronilor cu viteze foarte mari de suprafata unui metal.
Dispozitivul experimental
este format dintr-un tub cu vid inaintat (![]() ) un catod K incandescent si un anticatod A.
) un catod K incandescent si un anticatod A.
Diferenta de potential de accelerare intre catod si anticatod este de ordinul 10-100kV.
Radiatiile X produse au fost puse in evidenta datorita proprietatilor lor de a produce fluorescenta unor substante ca de exemplu platinocianura de bariu sau de a impresiona placa fotografica.
Studiile experimentale asupra radiatiei Rntgen au scos in evidenta ca acestea sunt de natura electromagnetica cu lungimea de unda λ cuprinsa intre 0,1-100Ǻ.
Spectrul radiatiei X emise este continuu peste care se suprapune un spectru de linii caracteristice elementului din care este facuta anticatoda.
Spectrul continuu se datoreste efectului fotoelectric invers. La frinarea electronilor de catre nucleele anticatodului, energia electronilor este emisa total sau partial sub forma de radiatie de franare.
In general electronii nu cedeaza energia lor instantaneu ci treptat si fiecare proces de emisie este responsabil de o frecventa din spectrul continuu.
Limita inferioara ![]() pentru lungimile de unda din spectrul radiatiei X corespunde
situatiei cind energia cinetica a electronului se transforma intr-o cuanta de
energie
pentru lungimile de unda din spectrul radiatiei X corespunde
situatiei cind energia cinetica a electronului se transforma intr-o cuanta de
energie  fara a putea
produce excitarea unui atom
fara a putea
produce excitarea unui atom
(28)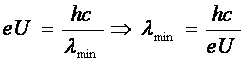 (29)
(29)
Astfel pentru un potential
de accelerare de U=10kV, λmin a
spectrului continuu al radiatiei X va fi ![]() .
.
Aceasta valoare este in concordanta cu valorile obtinute experimental prin difractia razelor X pe cristale, ceea ce demonstreaza caracterul cuantic al radiatiei electromagnetice.
Efect Compton
Caracterul corpuscular al radiatiei electromagnetice a fost confirmat si de efectul Compton. Se observa ca in urma unor experiente privind difuzia radiatiei X prin substanta, in componenta difuzata, pe linga radiatiile incidente mai apar si radiatii cu lungimi de unda mai mari decit ale acestora. Acest fenomen de aparitie in componenta difuzata a unor lungimi de unda mai mari decit a incidentei a fost denumit efect Compton. Efectul Compton nu poate fi explicat daca consideram ca radiatia electromagnetica are numai un caracter ondulatoriu.
Radiatiile X fiind electromagnetice ar trebui sa se comporte in ceea ce priveste difuzia ca si undele luminoase. Conform acestei teorii, radiatia difuzata rezulta din vibratiile electronilor provocate de radiatia incidenta si deci trebuie sa aiba aceiasi frecventa ca si a acestora.
Aplicind teoria cuantica, difuzia radiatiilor X trebuie considerata ca un proces de ciocnire elastica intre fotonii incidenti si electronii substantei aflati in repaos.
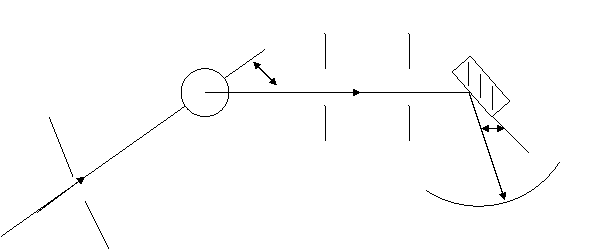
Dispozitivul prin care s-a pus in evidenta difuzia radiatiilor X de catre Compton este:
θ
![]()
![]()
![]() film fotografic
film fotografic
Asupra unei substante
difuzate, de exemplu grafit (R) se trimite un fascicul ingust de radiatii X de
o anumita lungime de unda cunoscuta prin fanta de plumb F1. Din fascicolul difuzat
de raze X de catre grafit sub un unghi φ, se separa un fascicol ingust cu
ajutorul fantelor de plumb F2 si F3. Acest fascicol intra intr-un spectrograf
de raze X cu retea cristalina P. Cu ajutorul unui film fotosensibil se
inregistreaza si apoi se masoara distributia spectrala a radiatiilor. Asa cum
am aratat, in radiatia X difuzata de radiatorul R de grafit sub un unghi
φ, pe linga radiatia cu lungimea de unda λ, se afla si o radiatie cu ![]()
S-a constatat experimental
ca: ![]() creste cu cit creste unghiul de difuzie φ. Aceasta deplasare nu depinde de lungimea de
unda incidenta si nici de natura substantei difuzante.
creste cu cit creste unghiul de difuzie φ. Aceasta deplasare nu depinde de lungimea de
unda incidenta si nici de natura substantei difuzante.
Pentru stabilirea relatiei
variatiei lungimii de unda vom considera ca un foton de energie hν se
ciocneste cu un electron cu masa de repaos ![]() . Aplicind legea de conservare a energiei si impulsului
inainte si dupa ciocnire se poate scrie:
. Aplicind legea de conservare a energiei si impulsului
inainte si dupa ciocnire se poate scrie:
(1)

![]()
![]() φ
φ
θ
![]()
Din figura rezulta:
(2)
sau:
(3)![]()
Scriind prima relatie (1) sub forma:
(4)![]()
si ridicand (4) la patrat obtinem:
(5) ![]()
Scazand din relatia (5) relatia (3) obtinem:
(6) ![]()
Tinand cont de relativitatea masei:
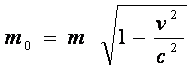 ,
,
atunci:

In acest caz relatia (6) devine:
![]()
(7) 
(8) 
Inlocuind  si
si 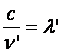 se obtine:
se obtine:
(9) 
Notam  se numeste lungimea de
unda Compton. Deci relatia devine:
se numeste lungimea de
unda Compton. Deci relatia devine:
(10) 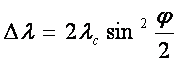
In radiatia difuzata se observa frecvent si o radiatie a carei lungime de unda este egala cu cea a radiatiei incidente. Aceasta arata ca fotonii in afara ciocnirilor cu electronii slab legati ai atomilor de la suprafata corpului difuzat, mai produc ciocniri si cu electroni din interiorul corpului difuzat. Acesti electroni de adancime fiind puternic legati de atomi, ciocnirea are de fapt loc intre fotoni si atomi a caror masa este mult mai mare decat a fotonului, ca urmare nu are loc nici un transfer de energie de la fotonul incident la atomul ciocnit si deci o parte din radiatia incidenta de raze X difuzeaza cu aceeasi lungime de unda.
Rezultatele experimentale asupra efectului Compton precum si concordanta lor cu teoria confirma ca radiatia electromagnetica se manifesta ca un flux de particule (fotoni) avand o anumita energie si un anumit impuls.
Presiunea luminii
Este un fenomen de asemenea legat de interactiunea radiatiei cu substanta. Existenta presiunii luminii a fost semnalata de Kepler, in incercarea de a explica orientarea cozilor cometelor fata de soare.
Fenomenul acesta,prin care
lumina produce o presiune asupra corpurilor a fost analizat si de Maxwell, care
i-a dat o interpretare pe baza teoriei electromagnetice a luminii. Lumina fiind
o unda electromagnetica, transversala, cand aceasta cade pe un mediu conductor,
vectorul electric ![]() din planul suprafetei iluminate, actionand asupra
electronilor liberi de conductibilitate,provoaca un curent electric paralel cu
din planul suprafetei iluminate, actionand asupra
electronilor liberi de conductibilitate,provoaca un curent electric paralel cu ![]() . Din interactiunea dintre acest curent si campul magnetic
. Din interactiunea dintre acest curent si campul magnetic ![]() , cealalta componenta a undei electromagnetice, ia nastere o
forta electromagnetica perpendiculara pe planul format de
, cealalta componenta a undei electromagnetice, ia nastere o
forta electromagnetica perpendiculara pe planul format de ![]() si
si ![]() , deci in directia incidentei luminii.
, deci in directia incidentei luminii.
Dupa calculele lui Maxwell, presiunea corespunzatoare acestei forte este proportionala cu intensitatea fascicolului incident.
In cazul cand razele de lumina formeaza un fascicol paralel, valoarea presiunii este egala cu densitatea de energie luminoasa w. In cazul acesta se presupune ca, corpul asupra caruia cade lumina este un corp absolut negru (r=0).
Daca factorul de reflexie r≠0 si are o valoare oarecare r, atunci presiunea devine:
(1) 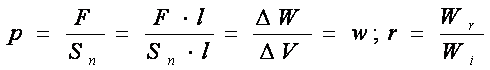 (2)
(2)
(3) ![]()
(4) ![]()
Pentru o oglinda perfecta cu r = 1, rezulta p = 2w
Daca tinem cont de intensitatea fascicolului incident:
(5) 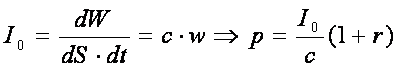 (6)
(6)
Maxwell a calculat forta
cu care apasa razele solare intr-o zi senina pe ![]() de suprafata neagra:
de suprafata neagra: ![]() .
.
Presiunea luminii a fost interpretata si calculata mult mai simplu cu ajutorul teoriei corpusculare asupra luminii.
Daca pe unitatea de suprafata asezata perpendicular pe directia de propagare si in unitatea de timp cad N fotoni, atunci intensitatea fascicolului va fi:
(7) 
Impulsul unui foton fiind ![]() , variatia impulsului in unitatea de timp, cand radiatia
luminoasa
, variatia impulsului in unitatea de timp, cand radiatia
luminoasa ![]() cade pe o suprafata
absorbanta (A=1); reprezinta valoarea presiunii:
cade pe o suprafata
absorbanta (A=1); reprezinta valoarea presiunii:
(8) 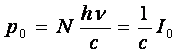
In cazul unei suprafete perfect reflectatoare, cand r=1, presiunea va fi data relatia:
(9) 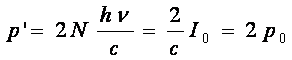
In general, in cazul unei
suprafete cu factorul de refexie r, din N fotoni incidenti vor fi refectati ![]() si absorbiti
si absorbiti ![]() . Variatia impulsului in unitatea de timp,pe unitatea de
suprafata asezata normal la directia de miscare a fotonilor, adica presiunea:
. Variatia impulsului in unitatea de timp,pe unitatea de
suprafata asezata normal la directia de miscare a fotonilor, adica presiunea:
(10) 
(11) 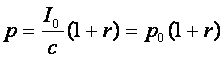
Relatia este identica cu cea obtinuta de Maxwell pe baza teoriei electromagnetice a luminii. Fenomenul de presiune a luminii se poate interpreta in general atat prin teoria electromagnetica clasica, cat si prin teoria fotonica a radiatiei. Acest fenomen a contribuit, de exemplu, la explicarea formarii cozilor de cometa, in partea opusa a Soarelui. Cand cometa se apropie suficient de Soare, presiunea luminii provenita de la acesta, respinge fluxul particulelor de dimensiuni mici din care este construita cometa.
In cazul acesta repulsia exercitata de Soare este mai mare decat atractia. Este un fenomen complex si fenomenul de presiune al luminii nu-l poate explica in intregime.
III. Natura ondulatorie a microparticulelor
1. Ipoteza lui de Broglie
In anul 1924 Louis de Broglie, pornind de la ideea dualitatii unda-corpuscul a radiatiei electromagnetice, arata ca acest caracter trebuie sa se extinda si asupra altor fenomene si anume la microparticule. Astfel el emite ipoteza: fiecarei microparticule in miscare rapida, electroni, protoni, atomi, ioni, etc., i se poate asocia o unda, numita unda de Broglie. Microparticulele manifesta proprietati ondulatorii alaturi de cele corpusculare.
Daca o particula se comporta ca o unda, atunci se pune problema determinarii lungimii de unda si a frecventei acestei unde, stabilirea relatiei dintre aceste marimi si energia si impulsul microparticulei in miscare.
In conformitate cu teoria
fotonica a lui Einstein, radiatia electromagnetica (in particular lumina) are
un caracter dual, adica prezinta atat proprietati ondulatorii, caracterizate
prin λ si ν, cat si prin proprietati corpusculare, caracterizate prin
valorile energiei ![]() si impulsul
si impulsul ![]() ale cuantei de lumina
(fotonului).
ale cuantei de lumina
(fotonului).
(1) 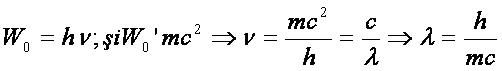 (2)
(2)
unde m*c este impulsul fotonului, iar λ, lungimea de unda a radiatiei electromagnetice.
Louis de Broglie
generalizeaza aceasta teorie, asociind oricarei microparticule in miscare cu
viteza ![]() si impulsul
si impulsul ![]() , o unda numita " unda asociata" cu lungimea de unda λ
data de o relatie similara cu cea in cazul luminii si anume:
, o unda numita " unda asociata" cu lungimea de unda λ
data de o relatie similara cu cea in cazul luminii si anume:
(3)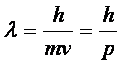
unde λ reprezinta lungimea de unda de Broglie, iar p este impulsul microparticolei care poate fi exprimat prin relatia relativista:
(4) 
Daca introducem vectorul ![]() al numarului de unda
al numarului de unda ![]() , impulsul microparticulei se poate exprima prin relatia:
, impulsul microparticulei se poate exprima prin relatia:
(5) 
Daca o particula se
comporta ca o unda, aceasta unda se poate descrie printr-o functie de unda ![]() care poate fi
reprezentata in cazul undei plane sub forma:
care poate fi
reprezentata in cazul undei plane sub forma:
(6) ![]()
In ceea ce priveste semnificatia functiei de unda (6) s-a pus problema daca aceasta trebuie identificata cu structura particulei insasi, sau caracterizeaza numai miscarile posibile ale acesteia.
Prima incercare de a da o interpretare legaturii dintre aspectele ondulatorii si corpusculare ala unei particule aflate in miscare a fost facuta de Schrdinger.
Conform intrepretarii sale, particula trebuie identificata cu un pachet de unde, care se obtine prin suprapunerea unui mare numar unde sinuisoidale de frecvente apropiate. Cu alte cuvinte particula trebuie considerata ca formata din unde.
Marimea ![]() reprezinta densitatea de distributie in spatiu a pachetului de unde si deci a particulei insasi.
Deci, conform conceptiei lui Schrdinger, functia de unda de Broglie este
legata direct de structura particulei.
reprezinta densitatea de distributie in spatiu a pachetului de unde si deci a particulei insasi.
Deci, conform conceptiei lui Schrdinger, functia de unda de Broglie este
legata direct de structura particulei.
Totusi aceasta interpretare a fost abandonata, deoarece, pe de o parte undele dintr-un pachet se imprastie cu timpul, iar pe de alta parte descrierea interactiunii a 2 particule ca o ciocnire dintre doua pachete de unda intampina dificultati.
O alta interpretare, mult mai acceptata in prezent, este interpretarea statistica a functiei de unda propusa de Max Born.
Conform acestei
interpretari, patratul modulului functiei de unda Broglie ![]() caracterizeaza
densitatea probabilitatii de localizare
in spatiu a particulei. Mai exact marimea
caracterizeaza
densitatea probabilitatii de localizare
in spatiu a particulei. Mai exact marimea ![]() reprezinta probabilitatea
ca la momentul t particula sa fie localizata undeva in elementul de volum dV.
reprezinta probabilitatea
ca la momentul t particula sa fie localizata undeva in elementul de volum dV.
Interpretarea
lui Max Born nu leaga functia de unda de Broglie de structura insasi a particulei. Odata cu schimbarea in
timp a functiei de unda ![]() se modifica
probabilitatea de a gasi particula in diferite puncte din spatiu.
se modifica
probabilitatea de a gasi particula in diferite puncte din spatiu.
Valoarea ipotezei lui de Broglie este atat mai mare cu cat, ea a fost emisa intr-o perioada in care nu exista nici un fapt experimental care sa o justifice.
Abia dupa emiterea ei s-au intrepins diferite experimente pentru a pune in evidenta caracterul ondulatoriu al microparticolelor aflate in miscare. Cateva dintre aceste experimente, care au confirmat ipoteza lui Broglie, vor fi prezentate in continuare.
2. Confirmarea experimentala a ipotezei lui de Broglie
Ipoteza lui de Broglie a fost foarte repede confirmata experimental. In 1925, la un an dela publicarea acestei ipoteze de catre de Broglie, Elsasser, este primul care arata prin calcul ca undele asociate electronilor in miscare au lungimea de unda de ordinul radiatiilor X. Legatura dintre λ a undei asociate si energia microparticulei se exprima prin relatia:
(7) 
Pentru un flux de
electroni accelerati intr-un camp electric, avand conditia ca ![]() , e - sarcina electronului, U - tensiunea electrica de
accelerare, ecuatia (7) devine:
, e - sarcina electronului, U - tensiunea electrica de
accelerare, ecuatia (7) devine:
(8) 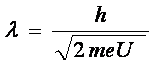
Daca in relatia (8) introducem valorile numerice pentru constanta lui Planck, masa electronului si sarcina acestuia e, obtinem relatia de calcul a lungimii de unda:
(9) 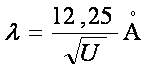
unde U este exprimat in volti. Astfel pentru U=100V, λ=1,225![]() .
.
Lungimile de unda, ale undelor de Broglie fiind de ordinul de marime a lungimii de unda a razelor X, trebuie sa produca ca si acestea fenomene de difractie si interferenta in cristale.
Primele experiente de difractie a undelor de Broglie au fost realizate de Davisson si Germer in anul 1927, prin refexia electronilor pe o suprafata a unui monocristal de nichel.
Un fascicol de electroni dintr-un filament incadescent sunt accelerati la o diferenta de potential U. Se obtine un fascicol ingust de electroni monocinetici (prin montajul folosit) care este trimis spre un monocristal de nichel.
Colectorul D, conectat la un amplificator , masoara, cu ajutorul unui miliamperimetru, intensitatea fluxului de electroni reflectat sub diferite unghiuri.
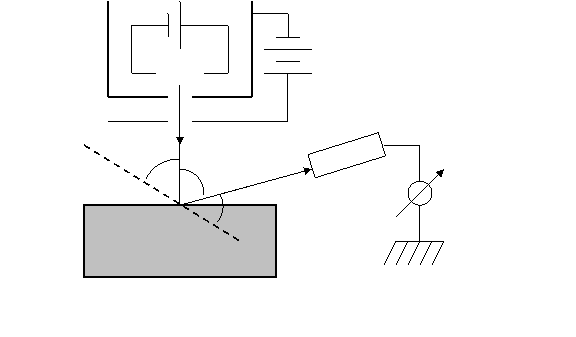
![]() U D P θ α mA Ni
U D P θ α mA Ni
directia fascicolului incident directia fascicolului reflectat

![]() Intensitatea
fascicolului
Intensitatea
fascicolului
0 U=54v reflectat
In urma masuratorilor efectuate s-a constatat ca intensitatea fascicolului de electroni reflectat prezinta maxime si minime a caror pozitie unghiulara depinde de energia electronilor incidenti.
Daca se traseaza curbele de variatie a intensitatii fascicolului de electroni reflectati in functie de unghiul dintre fascicolul incident si cel reflectat, se observa ca, curba obisnuita prezinta un maxim pentru un anumit unghi α, care depinde de viteza electronilor incidenti.
Unghiurile corespunzatoare maximelor satisfac relatia lui Bragg:
(10) 
unde d este distanta dintre doua plane reticulare ale retelei cristaline a
nichelului. In cazul nichelului, d=2,15![]() , pentru o tensiune de accelerare U=54V, unghiul ce
corespunde maximului de intensitate este
, pentru o tensiune de accelerare U=54V, unghiul ce
corespunde maximului de intensitate este
![]()
(dintre directia fascicolului incident si a celui reflectat). Introducand
aceste valori in relatia (10) si pentru n=1 se obtine λ=1,65![]() .
.
Pe
de alta parte introducand valoarea U=54V in relatia (8) se obtine ![]() .
.
Cele doua valori, cea obtinuta experimental si cea obtinuta teoretic sunt in buna concordanta. Concordanta este si mai buna daca se face corectia relativista a variatiei masei electronilor cu viteza.
Avand in vedere ipoteza lui de Broglie s-a conchis ca in acest experiment este vorba de un fenomen de difractie a electronilor, in urma reflexiilor acestora pe diferite plane ale retelei cristaline de nichel.
S-au facut experiente utilizand si metoda Debye-Scherrer. S-a obtinut in acest caz o figura de difractie sub forma unor inele.
Relatia lui de Broglie se aplica nu numai electronilor ci si protonilor, neutronilor, nucleelor, atomilor, moleculelor, ionilor, etc.
Insa datorita masei relativ mare a acestora, lungimile de unda corespunzatoare sunt foarte mici.
Cu toate acestea s-au observat experimental difractia fascicolelor de atomi de heliu sau moleculelor de hidrogen pe cristale de fluorura de litiu(LiF).
3. Relatiile de imprecizie ale lui Heisenberg
In mecanica clasica miscarea unei particule este complet determinata daca, pe langa fortele ce actioneaza asupra sa se cunoaste pozitia si impulsul la momentul initial. Aceasta situatie a fost folosita cu mult succes in lumea macroscopica, de exemplu, in astronomie. Un exemplu din astronomia contemporana il constituie masurarea precisa a pozitiei Lunii, cu ajutorul unui semnal radar care se reflecta, pe ea.
Miscarea Lunii este perturbata de masuratoare, dar datorita masei ei mari, aceasta peturbare se poate neglija. La o scara mai mica, de exemplu, in experimentele macroscopice de pe Pamant, astfel de perturbatii sunt de asemenea mici. Prin urmare a fost natural ca in fizica clasica sa se admita ca si in lumea sistemelor microscopice, pozitia si impulsul unui obiect, cum ar fi electronul, pot fi determinate precis prin observatii.
Heisenberg si Bohr au studiat aceasta ipoteza si au aratat ca: cu cat pozitia unei microparticule este cunoscuta cu o precizie mai mare, cu atat mai mare este nedeterminarea impulsului sau si invers, cu cat impulsul este cunoscut cu o precizie mai mare cu atat nedeterminare pozitiei particulei este mai mare.
Principiul de nederminare al lui Heisenberg este exprimat prin relatia:
(11)![]()
Interpretarea
fizica a acestei relatii se poate da
astfel: daca se cunoaste pozitia unei particule cu o imprecizie ![]() , atunci impulsul particulei poate fi cunoscut cu o
imprecizie mai mare sau egala cu
, atunci impulsul particulei poate fi cunoscut cu o
imprecizie mai mare sau egala cu ![]() si invers.
si invers.
Acest lucru este total diferit de cel din mecanica clasica, in care impulsul si pozitia unei particule pot fi determinate in principiu cu orice precizie dorita.
Deci admiterea naturii ondulatorii a unei microparticule impune imprecizii in determinarea pozitiei si impulsului.
Stabilirea relatiei de nedeterminare a lui Heisenberg se poate face si printr-o experienta de difractie a unui flux de electroni monocinetici printr-o fanta de difractie cu deschiderea "a".
![]()

![]() a
a ![]() α 0
α 0 ![]() x
x
Din
punct de vedere ondulatoriu fascicolul de electroni se comporta ca o unda plana cu lungimea de unda λ,
incidenta la fanta "a". Se
produce un fenomen de difractie la care franjele intunecate corespund unghiurilor ![]() , dupa relatia:
, dupa relatia:
![]()
Primul minim de difractie al fascicolului de electroni corespunde unghiului α pentru care n=1:
(12)![]()
Din punct de vedere corpuscular, tabloul de difractie da distributia statistica pe ecran a numarului de electroni difuzati in diferite directii la trecerea prin fanta.
Pentru un singur electron ce soseste pe ecran nu se cunoaste exact locul pe unde a trecut el prin fanta, ci doar faptul ca a trecut prin ea. Prin urmare imprecizia in masurarea coordonatei sale x de pe fanta este de ordinul largimii fantei, adica:
(13) ![]()
In ceeace priveste componenta impulsului dupa directia x, exista de asemenea o imprecizie asupra valorii ei si din tabloul de difractie rezulta ca electronii vor avea o componenta a impulsului de-a lungul axei x, deoarece au fost difuzati (li s-a schimbat directia).
Daca pentru α se
alege un unghi mediu de difuzie, deoarece nu se poate cunoaste exact locul unde
un singur electron atinge ecranul, atunci imprecizia ![]() in componenta dupa
directia x a impulsului unui singur electron este de ordinul:
in componenta dupa
directia x a impulsului unui singur electron este de ordinul:
(14)![]()
atunci:
(15) ![]()
sau daca folosim relatia (12) si
formula lui de Broglie 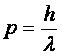 , relatia (15) devine:
, relatia (15) devine:
(16) ![]()
Daca se tine cont si de minimile de difractie de ordinul n, atunci relatia (16) devine:
(17) ![]()
sau in general:
(18) ![]()
Trebuie aratat ca limitarea impusa cunoasterii simultane a pozitiei si impulsului microparticulelor nu depinde de precizia instrumentelor si a aparatelor utilizate la observatii, ci este vorba de natura duala obiectiva a microparticolelor.
Experimentele efectuate dupa aparitia teoriei lui de Brogle, au aratat ca legile mecanicii clasice nu sunt aplicabile in cazul microparticulelor sau extinderea lor este mult limitata.
Relatiile de imprecizie a lui Heisenberg indica tocmai limitele aplicabilitatii ale mecanicii clasice in domeniul microparticolelor.
Sa consideram cateva exemple pentru a ilustra limitele de aplicabilitate ale relatiilor de imprecizie ale lui Heisenberg.
a)
Sa consideram o particula in miscare, cu masa ![]() , la care determinarea
coordonatei s-a facut cu o imprecizie foarte mica
, la care determinarea
coordonatei s-a facut cu o imprecizie foarte mica ![]() . In acest caz imprecizia pentru componenta vitezei pe
directia x se stabileste din relatia (18) si anume:
. In acest caz imprecizia pentru componenta vitezei pe
directia x se stabileste din relatia (18) si anume:
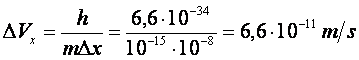
Rezultatul arata ca viteza particulei a fost calculata cu o foarte mare precizie.
b)
Viteza unui fascicol de electroni accelerati intr-un tub catodic este la un moment dat ![]() si a fost determinata
cu o imprecizie
si a fost determinata
cu o imprecizie ![]() .
.
Imprecizia coordonatei x a electronilor va fi:
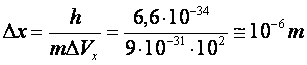
si in acest caz se constata ca precizia determinarii coordonatei electronului este foarte mare si permite sa se vorbeasca despre traiectoria electronilor in tubul catodic, traiectorie mult mai mare decat lungimea de unda de Broglie.
c) Sa urmarim miscare unui
electron pe traiectoria sa in jurul unui nucleu a unui atom. Deoarece
dimensiunile atomului sunt de ordinul ![]() m, este natural in cazul cel mai favorabil sa se poata
calcula coordonata electronului cu o imprecizie de ordinul dimensiunilor
atomului, adica:
m, este natural in cazul cel mai favorabil sa se poata
calcula coordonata electronului cu o imprecizie de ordinul dimensiunilor
atomului, adica: ![]() m.
m.
Atunci imprecizia in calcularea vitezei electronului este:
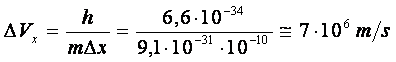
Insa viteza electronului in atom este de ordinul ![]() , asta inseamna ca viteza electronului in cadrul
atomului este practic nedeterminata.
, asta inseamna ca viteza electronului in cadrul
atomului este practic nedeterminata.
Astfel electronul in interiorul atomului nu poate fi considerat ca o particula in sensul particulelor macroscopice. Din aceasta cauza modelul cuantic al atomului nu este acesibil unei reprezentari intuitive.
d) O miniparticula in miscare pe directia 0x are energia:
(19) 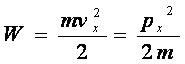
Daca impulsul s-a calculat cu o
imprecizie ![]() , atunci imprecizia in determinarea energiei W, este data prin diferentierea
relatiei (19):
, atunci imprecizia in determinarea energiei W, este data prin diferentierea
relatiei (19):
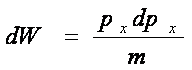
(20)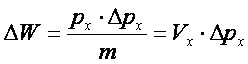
Se noteaza cu ![]() intervalul de timp in
care microparticula are energia
intervalul de timp in
care microparticula are energia ![]() .
.
Imprecizia la determinarea pozitiei sale este:
(21) ![]()
Din relatiile (20) si (21) rezulta ca:
![]()
sau in general:
(22) ![]()
Imprecizia energiei unei microparticule este cu atat mai mare cu cat timpul de existenta a microparticulei intr-o stare energetica W este mai mic.
De exemplu, un atom poate
ramane un timp infinit de lung pe nivelul fundamental, ![]() , atunci energia acestei stari este perfect definita
si deci
, atunci energia acestei stari este perfect definita
si deci ![]() .
.
Intr-o
stare energetica superioara, atomul ramanand un timp foarte scurt, imprecizia
energiei starii va fi  , in aceasta conditie energia starii va fi
, in aceasta conditie energia starii va fi ![]() .
.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2030
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved