| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Teoremele generale in dinamica corpului au aceeasi forma ca si corespondentele lor din dinamica punctului material, cu observatia ca marimile fundamentale care apar in aceste teoreme au expresiile specifice corpului. In afara de acestea, trebuie de fiecare data mentionat sistemul de referinta in raport cu care se lucreaza, deoarece in cazul in care marimile respective se exprima fata de sistemul de referinta atasat, derivatele lor in raport cu timpul vor respecta regula de derivare absoluta a unui vector variabil.
Conform teoremei omonime din dinamica punctului material:
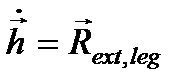 (1.1)
(1.1)
derivata in raport cu timpul a impulsului unui punct material in miscare este egala cu rezultanta tuturor fortelor care actioneaza asupra sa (forte exterioare si de legatura exterioare
Pentru un corp rigid, teorema va avea aceeasi forma, deoarece fortele interioare se anuleaza doua cate doua. Tinand seama de relatia pentru impulsul unui corp, se obtine:
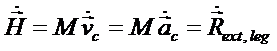 (1.2)
(1.2)
Tnand seama de ultima egalitatea din teorema (1.2), aceasta mai poarta numele de teorema de miscare a centrului de masa.
In cazul in care corpurile sistemului se studiaza izolat, membrul drept al teoriei va contine toate fortele exterioare si de legatura cu exteriorul care-i revin din ansamblul acestor forte aplicate sistemului, la care se adauga fortele de legatura cu celelalte corpuri din sistem (forte de legatura interioare). Astfel, pentru corpul i al unui sistem format din n corpuri, teorema se scrie:
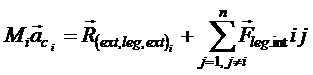 (1.3)
(1.3)
Teorema impulsului se proiecteaza pe axele sistemului de referinta, conducand la trei ecuatii scalare:
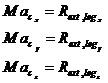 (1.4)
(1.4)
In cazul in care corpul sau sistemul de corpuri este izolat fata de exterior, sau daca prin reducerea sistemului de forte exterioare si de legatura se obtine un torsor cu rezultanta nula, impulsul sistemului respectiv se conserva:
![]() (1.5)
(1.5)
Ecuatia (1.5) reprezinta teorema de conservare a impulsului pentru un corp, un sistem de corpuri sau, in general, pentru un sistem material.
Aceasta teorema se mai poate interpreta si sub forma: intr-un sistem izolat, centrul de greutatea se deplaseaza rectiliniu si uniform. Cand constanta este nula, sistemul respectiv se afla in repaus.
Nu este obligatoriu ca impulsul sa se conserve integral. Cand proiectia rezultantei este nula pe o anumita directie din spatiu, teorema de conservare a impulsului este valabila numai pe directia respectiva.
Teorema impulsului se foloseste pentru determinarea legii de miscare a centrului de masa a corpului studiat, precum si pentru aflarea fortelor de legatura necunoscute.
Enuntata sub forma:
Pentru un punct material in miscare, derivata in raport cu timpul a momentului cinetic calculat fata de un punct oarecare, este egala cu momentul rezultant al tuturor fortelor exterioare si de legatura care actioneaza asupra punctului respectiv
si avand expresia,
![]() (1.6)
(1.6)
Cand insa corpurile sistemului se studiaza izolat, atunci pentru corpul oarecare i, in membrul drept al teoremei vor aparea fortele exterioare si de legatura cu exteriorul care-i revin din ansamblul celor aplicate sistemului, precum si fortele de legatura cu celelalte n-1 corpuri din sistem:
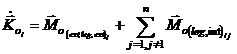 (1.7)
(1.7)
In cazul in care corpul sau sistemul sunt izolate, precum si in cazul in care al doilea element al torsorului de reducere este nul, momentul cinetic ramane constant:
![]() (1.8)
(1.8)
legea de mai sus reprezentand teorema de conservare a momentului cinetic.
Spre deosebire de cele doua teoreme vectoriale anterioare, teorema de variatie a energiei cinetice este o teorema scalara. Continutul sau este identic pentru punctul material, solidul rigid sau sistemele formate din acestea, adica pentru orice sistem material:
![]() (1.9)
(1.9)
exprimand egalitatea dintre variatia diferentiala a energiei cinetice si lucrul mecanic elementar al fortelor exterioare si de legatura, in intervalul elementar de timp cat se produce variatia respectiva.
In cazul in care fortele care actioneaza in sistem sunt forte conservatoare, lucrul mecanic elementar este diferentiala totala exacta a functiei de forta U si deci, lucrul mecanic finit nu depinde de traiectorie, fiind egal cu diferenta valorilor functiei de forta la capetele intervalului.
In aceasta situatie, teorema de variatie a energiei cinetice sub forma finita, este:
![]() (1.10)
(1.10)
care, tinand seama de definitia in cazul particular al lucrului mecanic al fortelor conservative, a energiei potentiale intr-o pozitie oarecare, devine:
![]() (1.11)
(1.11)
Grupand termenii dupa apartenenta la aceeasi pozitie rezulta:
![]() (1.12)
(1.12)
forma care exprima constanta energiei mecanice a sistemului.
Deci, intr-un sistem mecanic in care actioneaza doar forte conservative este valabila legea de conservare a energiei mecanice.
Aplicarea axiomei
legaturilor corpului astfel legat, conduce la introducerea unei singure
forte de legatura in punctul respectiv, reactiune
anormala ![]() , perpendiculara pe planul tangent comun si
dirijata spre corpul legat (Figura
1.1)
, perpendiculara pe planul tangent comun si
dirijata spre corpul legat (Figura
1.1)
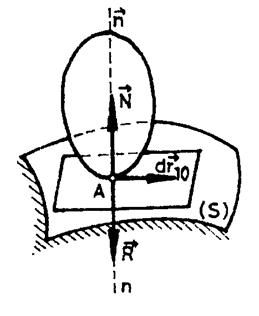
Figura 1.1
Se poate enunta principiul lucrului mecanic virtual in prima sa varianta:
In cazul unui sistem material supus la legaturi ideale, lucrul mecanic virtual al fortelor de legatura este nul
Forma matematica valabila a acestei formulari este de fapt relatia, cu caracterul general, de urmatoarea forma:
![]() (1.13)
(1.13)
Dar, problema care intereseaza nu este lucrul mecanic virtual al fortelor de legatura ci, cum sa fie inlaturate aceste forte, adica cum sa nu fie luate in considerare.
Se presupune, in acest scop, un corp in echilibru supus la legaturi ideale. Conditia necesara si suficienta pentru echilibru este ca torsorul fortelor exterioare si de legatura exterioare sa aiba elemente nule. Calculand in acest caz lucrul mecanic virtual al fortelor exterioare si de legatura se obtine:
![]() (1.14)
(1.14)
deoarece ambele paranteze din expresia (1.14) sunt nule.
Tinand seama de prima varianta deja enuntata a principiului lucrului mecanic virtual, prin scaderea relatiilor (1.14) si (1.13)
![]() (1.15)
(1.15)
Relatie care reprezinta cea de-a doua formulare a principiului lucrului mecanic virtual:
In cazul unui sistem material supus la
legaturi ideale si aflat in echilibru lucrul mecanic virtual al
fortelor exterioare este nul. Se presupune acum ca un sistem material
cu n grade de libertate se
afla in echilibru sub actiunea unui sistem de p forte exterioare
![]() si supus la
legaturi ideale. Fortele exterioare actioneaza in diferite
puncte ale sistemului, caracterizate de vectorii de pozitie
si supus la
legaturi ideale. Fortele exterioare actioneaza in diferite
puncte ale sistemului, caracterizate de vectorii de pozitie ![]() . Considerand legaturile olonome, vectorii de
pozitie au forma:
. Considerand legaturile olonome, vectorii de
pozitie au forma:
![]() (1.16)
(1.16)
fiind functie de cei n parametri scalari independenti qi si, eventual, in mod explicit, de timp.
Expresia lucrului mecanic virtual din relatia:
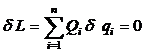 (1.16)
(1.16)
avand aceeasi forma ca si in
 (1.17)
(1.17)
marimile Qi poarta denumirea de forte generalizate. In timpul trecerii sistemului din starea caracterizata de parametrii qi in cea caracterizata de parametrii qi + qi se inregistreaza lucrul mecanic virtual al fortelor generalizate Qi. Astfel, Qi reprezinta o forta daca coordonata generalizata qi este o lungime si, respectiv, un moment, daca coordonata generalizata respectiva este unghi.
S-a obtinut astfel cea de-a treia formulare a principiului lucrului mecanic virtual:
Intr-un sistem material de echilibru, lucrul mecanic virtual al fortelor generalizate este nul.
Pentru cazul legaturilor olonome, se obtin un numar de n ecuatii scalare de echilibru de forma:
![]() (1.18)
(1.18)
Cu aceeasi precizare ca deplasarile virtuale qi sunt independente, se poate determina fiecare forta generalizata Qi prin calcularea lucrului mecanic virtual din sistem cand numai parametrul qi variaza. Raportand lucrul mecanic astfel obtinut la variatia virtuala a parametrului respectiv, se obtine forta generalizata cautata:
 (1.19)
(1.19)
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2348
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved