| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Sistem - ansamblu de elemente in interactiune, ce constituie un intreg unificat
- o entitate ce proceseaza un set de semnale (intrari) pentru a produce un alt set de semnale (iesiri)
Subsistem: sistem ce este parte a altui sistem
Exemple:
o roata → dispozitiv, dar un automobil → sistem!
Pamantul → element, dar cele 9 planete ce orbiteaza+ Soarele → sistemul solar!
In corpul uman (fiinte vii):
Sistemul nervos
Sistemul circulator
Sistemul digestiv
Sistemul reproductiv etc
TIPURI DE SISTEME
Sistem deschis: poate fi influentat de evenimente exterioare
Sistem inchis: care se autocontine, in sensul ca evenimentele exterioare nu-l influenteaza
Sistem mixt (deschis + inchis)
Sistem conceptual: unul realizat din idei
Sistem dinamic: unul care are componente sau fluxuri care se modifica in timp
Sistem fizic: unul care este realizat din si functioneaza cu masa si energie
Cutia neagra (black box) este o ilustrare convenabila a unui sistem, variabilele de intrare (cauze: m1(t), m2(t),.mj(t)) sunt aplicate, iar la alt set de terminale accesibile sunt observate variabilele de iesire (efecte: y1(t), y2(t),.yk(t))
Studiul sistemelor, trei arii majore:
1. Modelarea matematica (MM - vezi mai jos)
2. Analiza:
Cum se determina iesirile sistemului cand sunt date:
Intrarile sistemului si
Modelul sistemului (regulile de conducere a sistemului)
3. Proiectare (sinteza):
Cum se construieste un sistem care va produce un set dorit de iesiri cand sunt date
Intrarile sistemului
SISTEME clasificare
1 Sisteme lineare si nelineare
2 Sisteme cu parametri constanti si cu parametri variabili in timp
3 Sisteme instantanee (fara memorie) si dinamice (cu memorie)
4 Sisteme cauzale si necauzale
5 Sisteme cu parametri concentrati si cu parametri distribuiti
6 Sisteme in timp continuu si sisteme in timp discret
7 Sisteme analogice si digitale
1a-b. Sisteme lineare si nelineare
Linearitate avem atunci cand:
E valabil principiul suprapunerii (superpozitie, aditivitate), adica:
Daca mai multe cauze/intrari actioneaza asupra sistemului, efectul total asupra sistemului, datorat acestor cauze, se poate determina considerand fiecare cauza separat, in timp ce celelalte se considera a fi zero. Efectul total este suma tuturor efectelor componentelor.
E valabila proprietatea de omogenitate, adica:
Daca o cauza (intrare) creste de n ori, atunci efectul (iesirea) creste tot de n ori
Adica, iesirea sistemului este proportionala cu intrarea sa
Sisteme cu parametri invarianti si parametri variabili in timp
Cele cu parametri invarianti se mai numesc sisteme cu parametri constanti.
Caracteristici: Pentru orice stare initiala data, evolutia iesirii va depinde numai de forma (evolutia) intrarii si nu de momentul de timp la care se aplica aceasta.
3a-b. Sisteme instantanee (fara memorie) si sisteme dinamice (cu memorie)
a. Sisteme instantanee (fara memorie)-acelea la care iesirea acestora la orice moment de timp t, depinde, cel mult, de intensitatea intrarii(lor) la/din acelasi moment de timp, dar de niciuna din valorile trecute sau viitoare ale intrarii(lor).
b. Sisteme dinamice (cu memorie)- acelea la care iesirea depinde
b. Sisteme cu memorie finita acelea la care raspunsul la momentul de timp t este complet determinat de semnalele de intrare de pe trecutul (memoria) de T secunde [intervalul de la (t-T) la t]
Observatie: Sistemele instantanee sunt un caz special de s.dinamice
4a-b. Sisteme cauzale si necauzale
4a. Sistem cauzal (cunoscut si ca sistem fizic sau neanticipativ) - unul pentru care iesirea la orice moment de timp t0 depinde numai de valoarea intrarii f(t) pentru t ≤ t0, adica (la momentul respectiv), depinde numai de valorile trecute si prezente ale intrarii f(t), nu si de cele viitoare. Simplu: cauzal = nu avem iesire inainte de a se aplica intrarea. Sist. fizice sunt in mod necesar cauzale!
4b. Sistem necauzal (anticipativ) unul care violeaza conditia de mai sus (unul care poate raspunde la intrarile viitoare; unul profetic: cunoaste intrarea viitoare si actioneaza la aceasta in prezent!). Nu se poate construi in practica.
5a-b. Sisteme cu parametri concentrati si cu parametri distribuiti
5a. Sisteme cu parametri concentrati la care se presupune ca fiecare componenta a sistemului este concentrata intr-un singur punct in spatiu.
5b. Sistemele cu parametri distribuiti semnalele sunt functii de spatiu si detimp → MM cu EDP.
6a-b. Sisteme in timp continuu si sisteme in timp discret
6a. Sisteme in timp continuu acele sisteme ale caror intrari si iesiri, adica m(t) si y(t), sunt semnale in timp continuu, adica t :T→ℛ
6b. Sisteme in timp discret sisteme ale caror intrari si iesiri sunt semnale in timp discret, adica definite numai la momente discrete de timp t0, t1, t2, .,tk,, notate m(tk), y(tk) etc, k fiind un intreg oarecare.
7a-b. Sisteme analogice si digitale
7a. Semnal analogic acela a carui amplitudine poate lua orice valoare intr-o plaja continua (o infinitate de numere pentru valori)
7b. Semnal digital unul a carei amplitudine poate lua numai un numar finit de valori. Cele digitale asociate cu PC-uri digitale, sunt digitale deoarece iau numai doua valori (semnale binare adica; 0 sau 1, DA sau NU, tot sau nimic)
SISTEME AUTOMATE - SA
SA un dispozitiv sau un set de dispozitive conectate intr-o astfel de maniera incat controleaza/dirijeaza/conduce direct comportarea altui sistem
Tipuri de control (conducere, administrare):
Control logic
Control linear (cu feedback, cu reactie, in bucla inchisa)
Fuzzy control (control cu logica fuzzy)
SA clasificare dupa functia indeplinita:
Sisteme de control automat (SCtA) - SCADA etc
Sisteme de comanda automata (SCdA) secventiale, logice, PLCs etc.
Sisteme de reglare automata (SRA) !!!
Sisteme de protectie automata (SPA)
Sisteme de optimizare automata (SOA)
Alte tipuri de sisteme automate
Sisteme de reglare automata (SRA), iar aici:
Control conventional (PID etc)
Control adaptiv
Control H∞ (control robust)
Control predictiv bazat pe model
Control optimal
Control neliniar
Control inteligent (F-fuzzy, N-neuro(nal), NF, FN, AG-algoritmi genetici, SE-sisteme expert)
Tipuri de control/reglare
Controlul logic
Utilizeaza logica pura
Deci, ladder logic este mai degraba un limbaj bazat pe reguli decat un limbaj procedural! Exemple: la laborator.
Control linear (cu feedback/ reactie, in bucla, I)
C ![]()
![]()
![]()
|
|
Transformatele Laplace: R(s)E(s)U(s)Y(s)
Fuzzy control (control cu logica fuzzy, I)
Controlerele fuzzy se proiecteaza usor
O masurare intr-un sistem cu logica fuzzy poate fi si doar partial adevarata: adica, daca DA este 1, si NU este 0, o masuratoare fuzzy poate fi intre 0 si 1 (gri!, nu numai alb sau negru)
Regulile sistemului fuzzy se scriu in limbaj natural si apoi se translateaza in logica fuzzy. Exemplu: Daca presiunea este prea ridicata, atunci micsoreaza debitul de abur in turbina. Daca presiunea este prea scazuta, creste/ mareste debitul de abur in turbina.
Implementare logica fuzzy
LF = sistem ce rezolva o problema (→ o concluzie), bazat insa pe informatie vaga, ambigua, imprecisa, cu zgomot, sau incompleta.
Implementarea sistemelor LF: software, hardware, combinata
De la simple si mici embedded-C la multi-chanel PC sau workstation-based SCADA.
Problemele de FLC (FL-control) mimeaza modul uman de luare a deciziilor, dar mult mai repede. Exemple: aspiratoare, masini spalat rufe, avioane, fabrici de ciment, ventilatie tuneluri etc, etc
Formulari fuzzy si formulari exacte
Carmen este inalta
Carmen este inalta (deoarece are 1.78 m)
Carmen este inalta (fiindca este in echipa de baschet: in acest caz are 1.93 m)
Afara este frig
Iarna
Cand afara este - 6 C
Vara
Cand afara este + 6 C
Cand la munte (Bucegi etc) este +4 C etc.
Ce reprezinta acesti termeni din formularile fuzzy?
Logica fuzzy este o metoda noua de definire a modelelor sistemelor, regulilor si proceselor, utilizand limbajul vorbit, care este ambiguu sau fuzzy (vag).
Logica fuzzy nu este fuzzy in privinta modalitatii in care defineste modelele sistemelor, regulilor si proceselor, desi se poate considera pentru plasticitate.
Fuzzy control e util atunci cand metodele conventionale de control sunt scumpe or greu de aplicat
TIPURI DE MODELE
Cuvantul model are intelesuri diferite, functie contextul in care e utilizat:
1. Modele ca reprezentari (adica abstractizari)
2. Modele ca/de obiecte fizice
3. Modele de oameni
4. Modele in software
5. Nume propriu de model, utilizat de oameni (in moda, modeling), SC sau SA, organizatii etc
1. Modele ca reprezentari (adica abstractizari):
Modele abstracte (sau conceptuale constructii teoretice ale proceselor fizice, chimice, biologice, sociale (adica modele matematice-MM). Se utilizeaza variabilele specifice si legaturile logice si cantitative dintre acestea
Modele mentale- reprezentarea cunosterii unei persoane, a unei idei, a procesului de gandire
Teoria modelarii- studierea reprezentarii conceptelor matematice
La programarea neuro-lingvistica studierea structurii experientei subiective (Ce, cum si cand facem? Cum invatam? Cum gandim?).
Modelarea solidelor - reprezentarea corpurilor solide sau a partilor din acestea pentru procesare pe calculator (animatie, grafica, CAD-Computer Aided Design/drafting/assisted/design and drafting, realitate virtuala etc)
Produse software comerciale: AutoCAD, ECAD, MCAD, AEC, Catia, Pro/ENGINEER etc.
MODEL MATEMATIC- definitii
Un MM: o reprezentare matematica abstracta ce utilizeaza un limbaj matematic pentru a descrie comportarea unui sistem.
Definitie Eykhoff(1974): o reprezentare a aspectelor esentiale ale unui sistem, care prezinta cunoasterea starii intr-o forma uzuala
Scopurile unui model conceptual sunt
Furnizeaza un cadru de argumentari si evaluari, utilizand rationamente logice si matematice pentru diverse situatii, folosind testari repetate.
La evaluarea ipotezelor teoretice, ori la descoperirea de noi fapte sau proceduri experimentale.
La implementarea pe calculator a simularilor sistemelor, pentru a observa comportarea in timp a acestora.
La analiza, controlul si optimizarea sistemului fizic modelat, respectiv la:
Cercetare si dezvoltare (interpretarea cunoasterii, masuratorilor, date si statii pilot)
Proiectare (determinarea corecta a parametrilor, studierea aspectelor economice si de siguranta a procesului)
Planificare si scheduling (programare orara, calendaristica)
Optimizarea functionarii (simulari, simulari→ optimum)
Predictie si control (modelele se utilizeaza adesea la predictia valorilor variabilelor)
MODELAREA: procesul obtinerii unui model
Modelare → generarea unui model, ca o reprezentare conceptuala
Doua (sau mai multe) modele ale aceluiasi sistem/ fenomen, pot fi mult diferite intre ele.
Diferentele dintre modele pot fi cauzate de:
Cerintele si ipotezele de modelare diferite ale utilizatorilor modelului
Diferentele conceptuale ale modelatorilor
Consideratiile estetice diferite ale acestora
Preferintele acestora privind structura MM (probabilistic, deterministic, stochastic, in timp continuu, in timp discret etc)
Rezulta ca: utilizatorii unui MM trebuie sa inteleaga bine scopul initial al acestuia, ipotezele de modelare, unde se utilizeaza acesta (validitate).
Validitatea tuturor MM este limitata:
Din cauzele de mai sus
Din cauza acuratetei modelarii
Din cauza riscului utilizarii acestuia in exteriorul punctului sau ariei de lucru a acestuia
Rezulta ca un MM nu este niciodata adevarat sau exact
Rezulta ca in cel mai bun caz el este valid si posibil credibil
Rezulta ca intotdeauna trebuie sa fim critici cu un MM
Abordarea teoretica (analitica)
Reprezentarea realitatii se face prin intermediul ecuatiilor matematice care sunt:
ecuatii de bilanturi de energie (EDO, EDt
ecuatii de bilanturi de masa (EDO, EDt
ecuatii de bilanturi de momente (EDO, EDt) si deseori
ecuatii algebrice (transfer de masa, de energie, constante pentru diverse fenomene, reactii etc)
Abordare experimentala (identificare)
Se identifica intrarile si iesirile (I/E) procesului, dupa care se alege o tehnica adecvata pentru determinarea legaturii I/E.
Modelul dinamic (linear) empiric rezultat din datele procesului, poate fi:
EDO sau
EDt (cazul uzual, respectiv f.d.t. lineara discreta)
VARIABILELE MM
MM uzual descrie un sistem prin:
un set de variabile (reale, intregi, booleene, siruri etc) si
un set de ecuatii (stabilesc legatura dintre variabile)
Variabilele reprezinta proprietati ale sistemului (semnale, date, evenimente etc. ale I/E sau I/S/E aferente sistemului, masurate), si constituie impreuna cu setul de ecuatii/functii modelul matematic
Exista sase tipuri principale de variabile:
Variabile de intrare
Variabile de iesire - dependente de starea sistemului (variabilele de stare ale acestuia)
Variabile de stare variabile dependente de variabilele de decizie, de cele de intrare, de cele aleatoare si de cele exogene
Variabile de decizie (control/comanda)- cunoscute si ca variabile independente
Variabile aleatoare
Variabile exogene cunoscute si sub denumirea de parametri sau constante (variabile exterioare)
STRUCTURI de MM
Aplicatiile diferite ale modelelor, si scopurile de modelare diferite ale acestora conduc la structuri diferite de modele (1-6 a,b):
1a. MM lineare, la care:
Toate functiile obiectiv si toate constrangerile sunt numai ecuatii lineare
Se aplica la ele principiul suprapunerii, respectiv:
Daca α si β sunt constante, iar MM este de forma y = f(u), principiul superpozitiei statueaza ca αf(u1) + βf(u2) = f(α u1 + βu2)
Deseori MM dinamice lineare se utilizeaza ca o aproximare a realitatii
Totusi, daca plaja de functionare este limitata, MM lineare descriu cu suficienta acuratete realitatea.
1b. MM nelineare, la care:
Macar o functie obiectiv sau o constrangere este neliniara, MM e neliniar
Sunt greu de rezolvat analitic (met. numerice, v.Matlab, GNU Octave etc)
Se utilizeaza la optimizarea proceselor
STRUCTURI de MM
2a. MM deterministe (deterministice)
un MM care are acelasi fel de a fi (comportare identica), pentru un set dat de aceleasi conditii initiale
2b. MM stochastice (probabilistice, stohastice)
un MM la care este intotdeauna prezenta comportarea aleatoare/ stohastica, atunci cand sunt date aceleasi conditii initiale
3a. MM statice
Sunt MM la care legaturile dintre variabile (ecuatiile adica), nu sunt functii de timp
Variabilele MM statice nu au memorie
Ele sunt dependente numai de cele mai recente valori ale variabilelor independente
3b. MM dinamice
Sunt MM care tin seama de timp, la care ecuatiile sunt functii de timp; sunt reprezentate cu ecuatii cu diferente (EDt) sau ecuatii diferentiale ED) (adica au dinamica)
MM dinamice au memorie pentru starea lor, o pot descrie ca functie de timp la modificarea variabilelor independente (raspunsul tranzitoriu!)
Observatie: Diferenta dintre un MM dinamic si unul static, daca ambele sunt bazate pe ecuatii de continuitate, este aceea ca la cel static termenii ce reprezinta acumulari sunt setati la zero
4a. MM cu parametri concentrati
Sunt MM omogene, adica au starea consistenta in intregul sistem (au parametrii concentrati).
Parametrii concentrati sunt reprezentati prin EDt si prin ED ordinare (EDO).
Nu descriu variatiile spatiale, deci pot fi aproximatii ale realitatii
4b. MM cu parametri distribuiti
Sunt MM eterogene, starea lor variaza in interiorul sistemului (adica au parametrii distribuiti).
Parametrii distribuiti se reprezinta uzual cu ED partiale (EDP).
Variabilele de proces independente si proprietatile sistemului pot varia in lungul unei coordonate spatiale axiala, radiala, carteziana (R la cabluri, θ C la brame, θ si concentratia la reactoare chimice etc)
MM complex care ia in consideratie variatiile spatiale este un MM cu parameti distribuiti (element, celula, volum finit)
5a. MM continue (in timp continuu)
Sunt acele MM a caror variabile au valori la oricare moment de timp dat (variabile continue, timp continuu, adica t : T →R)
5b. MM discrete (in timp discret)
Acele MM care descriu starea sistemului numai la momente de timp discrete (la intervale de timp date; variabile discrete, timp discret, adica t : T →Z)
MM discrete necesita metode de rezolvare numerica
Calculul iesirii unui sistem cu calculatorul, necesita ca MM continue sa fie discretizate
Discretizarea ecuatiilor unui MM continuu: aproximarea derivatelor de ordinul ≥ 1 prin una dintre metodele de aproximare a diferentelor: inainte, in urma, sau centrala.
6a. MM in domeniul timp (t)
MM la care variabila independenta in ecuatiile de model este timpul (continuu t :R→R, sau discrett :Z→Z)
MM cu EDO (ecuatii diferentiale ordinare, I-E si I-S-E)
MM cu EDt (ecuatii cu diferente, I-E si I-S-E)
MM de stare (I-S-E, structural functionale)
6b. MM in domeniul frecventa (s, ω
MM la care variabila independenta este frecventa ω [rad/s], sau frecventa complexa s (s = σ + j ω
Caracteristica Nyquist (locul de transfer)
Caracteristicile Bode (castig-frecventa si faza-frecventa)
Caracteristica (diagrama) Nichols
Functii de transfer
7a MM cutie alba white box sau MM mecanice fizice MM bazate pe pricipiile primare adica pe legile fizice si chimice ale conservarii
Dau un inteles fizic al procesului, dar
Necesita eforturi mari pentru realizare. Se compun din:
Ecuatii de bilanturi de conservare (dinamica), deci EDO, EDt, respectiv:
Bilant de masa
Bilant de momente
Bilant de componente
Bilant de energie, impreuna cu,
Ecuatii algebrice ce descriu
Transferuri de masa
Transferuri de energie,
Cinetci diverse
MM cutie neagra (black box), sau modele empirice
Nu reflecta structura fizica a procesului
Se bazeaza pe date
Reflecta legaturile I/E ale procesului
Sunt utile atunci cand:
Timpul de dezvoltare a MM este limitat
Intelegerea fizica a procesului este incompleta
Intelegerea fizica a procesului lipseste
Aceste MM sunt:
Seriile de timp (ARMA, ARMAX, ARX etc)
RNA (Retele Neuronale Artificiale)
MM fuzzy
MM ale CMMP
7c. MM cutie gri (grey box):
Cand se dispune de cunoasterea procesului, dar anumite informatii sau cunostinte lipsesc
In astfel de situatii, se combina MM fizice (white box), cu MM black box: rezulta MM gri (grey box)
Exemple:
MM fizice + RNA
MM fizice + modele cu logica fuzzy
Nivelul de interpretare fizica ce poate fi dat MM este aratat proportional in figura, pentru modelele black-grey-white box

C2
Ecuatii diferentiale ordinare
Expresie diferentiala o functie care contine variabile si derivatele acestora
Ecuatie diferentiala(ED): o expresie diferentiala egalata cu zero.
EDO: o ED care contine numai o singura variabila independenta
EDP (ED Partiala): o ecuatie ce contine mai mult decat o singura variabila independenta.
Variabila independenta: oricare marime precum: timp, presiune,temperatura, distanta, viteza, acceleratie etc
Ordinul unei ED: valoarea/ ordinul celei mai mari derivate
Exemplul 1: (d3y/dt3)5 + 2.5(dy/dt) + 12y2(t) = cos(t)(1) este o EDO de ordinul trei, ordinul derivatei!
Exemplul 2 an(t)(dny/dtn)+an-1(t)(dn-1y/dtn-1)+..+a1(t)(dx/dt)+a0(t)y(t)=r(t) (2) este o EDO de ord. n (cea mai mare derivata)
EDO lineara: acea EDO la care coeficientii ai(t), bj(t) nu sunt functii de y(t)
EDO lineara cu coeficienti constanti: acea EDO la care toti coeficientii ai(t), bj(t), sunt constanti (valori numerice)
Solutia
O functie y(t) are o derivata unica(dy/dt), dar:
Pentru o derivata data (dy/dt), exista o infinitate de functii posibile, y(t).
Deci rezulta ca e imposibil sa determinam in mod unic pe y(t)
Totusi, putem determina in mod unic pe y(t), doar daca mai exista informatii suplimentre (constrangeri), despre ea (adica despre y(t)).
Solutia EDO de grad 2, 3, ,n, se poate determina in mod unic, doar daca avem 2, 3, .,n informatii suplimentare despre y(t).
Aceste informatii suplimentare se mai numesc constrangeri sau conditii suplimentare
Daca aceste conditii suplimentare sunt date la timpul t=0 (in origine), ele se numesc conditii initiale.
Metode de determ. a solutiei EDO
A). Metode in domeniul timp (t):
1. Ecuatii diferentiale ordinare
1.a. Metoda clasica (numai anumite intrari)
1.b. Metoda convolutiei (moderna, generala)
2. Ecuatii cu diferente
2.a. Solutie prin metoda clasica
2.b. Solutie prin metoda convolutiei
B). Metode in domeniul frecventa (s, ω
- Metoda transformatelor Fourier, Laplace, z
Ecuatii diferentiale ordinare
1.a)Solutia EDO clasica
Daca in ecuatia (3) avem u(t)=0, aceasta se numeste EDO omogena (sau complementara).
Se arata (fara demonstratie aici) ca solutia EDO este suma y(t)=yc(t)+yp(t), unde
yc(t) este solutia complementara
yp(t) solutia particulara
La analiza sistemelor automate LTI, cele doua solutii (raspunsuri ale sistemului) se numesc yn(t) raspuns natural, si yf(t) raspuns fortat, adica y(t)=yn(t)+yf(t)
Solutia complementara (raspunsul natural) aferenta EDO, yc(t) (numita si yn(t)), se poate determina daca si numai daca yc(t) si toate cele n derivate succesive ale acesteia au aceeasi forma (altfel, suma acestora, in (3), niciodata nu va tinde spre zero pentru toate valorile lui t).
Singura functie care are aceasta proprietate este functia exponentiala eλt, deci solutia EDO yc(t) este de forma yc(t)=cieλit, unde λi, i=1, 2,.,n, sunt solutiile ecuatiei caracteristice aferente EDO (polinomul caracteristic egalat cu zero).
De aceea, λi se numesc: -
radacini caracteristice, sau, alteori
valori caracteristice, sau
valori proprii (eigenvalues) sau
frecvente naturale.
Exponentialele eλit (i=1, 2, .,n), din solutia complementara yc(t) se numesc: - moduri caracteristice, sau, alteori
- moduri naturale, sau, simplu
- moduri
Observatia 1: exista cate un mod caracteristic pentru fiecarea radacina caracteristica
Observatia 2: solutia complementara yc(t) este o combinatie lineara de moduri caracteristice
Solutia particulara (numita si raspuns fortat) aferenta EDO, yp(t), se poate determina numai daca (nu in caz contrar):
Intrarea u(t) este ca forma a.i. rezulta numai un numar finit de derivate independente ale acesteia, respectiv cazurile:
u(t) exponentiala, est, o singura derivata independenta (diferentierea repetata a lui est este est);
u(t)=tm diferentierea repetata, duce la m derivate independente;
u(t)=k (constanta) diferentiala rezulta zero;
u(t)=cos(t) intrare sinusoidala;
u(t)=trest;
u(t)=ejt (s=jω), intrare exponentiala complexa.
Observatie: forma raspunsului fortat yp(t) este deci asemanatoare cu forma functiei u(t) aplicata la intrare
1.b Solutia EDO, m. convolutiei
Intrarea u(t) la aceasta metoda se exprima ca o suma de impulsuri
Solutia este obtinuta ca o suma a solutiilor aferente tuturor impulsurilor ce compun intrarea
Metoda se foloseste de proprietatea (principiul) superpozitiei, ce actioneaza numai la LTI LIT
Compararea celor doua metode
Metoda convolutiei este laborioasa, comparativ cu metoda clasica
Metoda clasica are dezavantajul ca duce la obtinerea raspunsului total, din care nu pot fi separate cele doua componente ce rezulta din conditiile interne si conditiile externe
La analiza SA este avantajos sa avem exprimat raspunsul sistemului la o intrare u(t), ca o functie explicita de u(t); cu metoda clasica nu e posibil acest lucru.
Metoda clasica nu se poate aplica la orice tip de intrare, ci doar la cateva tipuri (acele u(t) care au un numar finit de derivate independente)
Ecuatii cu diferente.
Metode de determinare a solutiei EDt
A). Metode in domeniul timp (t):
1. Ecuatii diferentiale ordinare
1.a. Metoda clasica (numai anumite intrari)
1.b. Metoda convolutiei (moderna, generala)
2. Ecuatii cu diferente (EDt)
2.a. Solutie prin metoda clasica
2.b. Solutie prin metoda convolutiei
B). Metode in domeniul frecventa (s, ω
- Metoda transformatei Laplace
Generalitati
Consideram doar EDt lineare cu coeficienti constanti
EDt se pot exprima in doua forme:
Prima, utilizeaza valorile din urma, cum sunt y[k-1], y[k-2], y[k-3], u[k-1], u[k-2], u[k-3],.etc (operator de intarziere)
A doua, utilizeaza termenii in avans, cum sunt y[k+1], y[k+2], y[k+3], u[k+1], u[k+2], u[k+3],.etc (operator in avans)
O EDt lineara generala, de ord. n, cu operator in avans este:
any[k+n]+an-1y[k+n-1]+..+a1y[k+1]+a0y[k] = bmu[k+m]+bm-1u[k+m-1]+..+b1u[k+1]+ +b0u[k]
unde, in membrul stang sau drept, y[k] sau u[k] sunt valorile acestor variabile la momentele de timp k+n, k+n-1, k+n-2, respectiv k+m, k+m-1 etc, etc.
Ecuatii cu diferente
Conditia de cauzalitate cere ca solutia EDt sa nu depinda de valorile viitoare ale intrarii (nu se poate!)
Deci, cu forma operatorului in avans (ec. de mai sus), cauzalitatea cere ca m ≤ n.
Ecuatia cu diferente cauzala generala este atunci cand m = n, respectiv, cu operator de avans:
any[k+n]+an-1y[k+n-1]+.+a1y[k+1]+a0y[k] = bnu[k+n]+bn-1u[k+n-1]+.+b1u[k+1]+b0u[k] (4)
Ecuatia cu diferente cauzala generala este atunci cand m = n, respectiv, cu operator de intarziere:
any[k]+an-1y[k-1]+.+a1y[k-n+1]+a0y[k-n] = bnu[k]+bn-1u[k-1]+..+b1u[k-n+1]+b0u[k-n] (5)
Transformate, generalitati: Fourier, Laplace, z
Fourier Jean-Baptiste-Joseph (1768-1830)
matematician francez, orfan la 8 ani, colegiu militar (calugari benedictini), sef catedra matematica la Ecole Normale (26 ani!), apoi la Ecole Polytechnique in Paris, baron, prefect de Paris, secretar al Academiei de Stiinta Paris, contemporan cu Napoleon, Laplace, Lagrange (1736 -1813), Legendre (1752-1833), Lavoisier (1743-1794);
contributii: algebra, teoria ED, teoria analitica a propagarii caldurii in corpurile solide, serii F., transformate F.(TF-in timp continuu-TFD si in timp discret, iar aici si TFR-FFT)
Laplace Pierre Simon, marchiz de (1749 - 1827) (transformata s!)
matematician, astronom si fizician francez, contemporan cu Napoleon, Fourier, Legendre, Lagrange
contributii: ED, EDO, EDP, teorie cosmogonica (Kant-Laplace), Tratat de mecanica cereasca, contributii in electromagnetism, generalizarea TF (adica integrandul are si factor exponentila real, nu numai imaginar, s = jω, respectiv transformarea este o functie de variabila complexa, s=σ + jω); transformt Laplace in timp discret este transformata z
Transformata z
este transformata Laplace pentru sisteme in timp discret, adica transformata Laplace deghizata, sau transformata Laurent-deoarece se bazeaza pe aceasta serie) , a fost introdusa cu acest nume, in anul 1958, de E.I. Jurie, in Sampled-Data Control, J. Wiley & Sons.
Familia Fourier
Cei patru membri ai familiei Fourier:
TFD (DFT)-Transformata Fourier Discreta
TFTD (DTFT)-Transf. Fourier in Timp Discret
TF (FT)- Transformata Fourier Continua (in timp continuu)
SF (FS)- Seria Fourier
Din tabel, se observa ca cele patru transformate ale familiei se caracterizeaza prin:
Cele doua domenii sunt temporal si frecvential (timp-frecventa)
Caracterul discret al unui domeniu implica periodicitate in domeniul conjugat (imaginar)
Continuitate intr-un domeniu implica aperiodicitate in domeniul conjugat
Domeniul real/ realitatea implica simetrie in domeniul conjugat
|
Trans- formata |
Timp |
Frec- Venta |
|
TF continua |
Continua, aperiodica |
Continua, aperiodica |
|
Seria Fourier |
Continua, periodica |
Discreta, aperiodica |
|
TF in timp discret (TFTD) |
Discreta, aperiodica |
Continua, aperiodica |
|
TF discreta (TFD-DFT) |
Discreta, periodica |
Discreta, periodica |
Transformate Fourier, interpretare in termeni de timp si frecventa
TF transforma o functie din domeniul timp (original, real) intr-o functie in domeniul frecventa
Adica, TF descompune functia din domeniul timp in armonici de diferite frecvente
Interpretarea obisnuita a acestei descompuneri (a functiei de timp, ce reprezinta un semnal fizic, de ex. tensiune, curent, turatie, nivel, pH etc), este aceea a spectrului de frecventa al semnalului.
Observatie: TF nu se utilizeaza numai la functii de timp si la frecvente temporale. TF pot fi utilizate la analiza frecventelor spatiale si functii avand orice fel de variabile reale/ domenii (adica nu numai functii de timp)
Transformata Fourier continua (TF) (t ∈ T → ℛ), (I)
Daca f(t) este o functie reala de variabila reala t (t are valori intre -∞ si +∞), atunci transformata Fourier (TF) a lui f(t) este definita prin relatia (TF continua aici, t ∈ T → ℛ
![]()

unde: - ω este frecventa in [rad/s];
- i=sqrt(-1)
- si e-iωt este exponentiala complexa data de relatia lui Euler:
e-iωt = cos(ωt) i sin(ωt)
Cu relatia lui Euler in cea de definitie, obtinem:
F(ω) = Re(ω) + i Im(ω
unde R(ω) si Im(ω) sunt partile reala si imaginara ale F(ω), care permit obtinerea i)spectrului amplificarii,
ii)spectrul de faza
Aplicatii:
In fizica, procesarea semnalelor,acustica, statistica, optica, geometrie, teoria probabilitatilor
Proprietati:
Descompune semnalul procesat in frecventele si amplitudinile sale componente
TF este un operator linear
Functiile de baza sinusoidale sunt functii proprii de derivare, adica, TF transforma EDO lineare cu coeficienti constanti in ecuatii algebrice ordinare.
Utilizand teorema convolutiei, TF transforma operatia de convolutie (complicata), intr-o simpla inmultire
TF discreta poate fi calculata rapid cu algoritmi TFR(FFT) utilizand calculatoare
TF este inversabila, TF inversa avand apropximativ aceeasi forma ca si TF directa (se observa din relatie ca TF in timp continuu reprezinta orice functie f(t), finita sau periodica, de patrat integrabil, ca o suma de exponentiale complexe ce au frecventele unghiulare ω si amplitudinile complexe F(ω :
Variante ale TF:
TF continua (in timp continuu, t ∈ T → ℛ
TF discreta (in timp discret t ∈ T → Z);
Seria Fourier
TFTD (DTFT) este un membru al familiei TF, ce transforma o functie f(n) ce are variabila n de timp discret (un sir), adica n ∈ T → Z.
Functia imagine obtinuta cu TFTD este un spectru continuu si 2π periodic, adica F(ejω) = F(ej(ω+2π
Transformata Fourier Discreta-TFD
(t ∈ T → Z),
TF discreta (TFD) se utilizeaza:
Numai daca functiile xk sunt definite in timp discret (t ∈ T → Z), si sunt finite si periodice, la:
Calcule stiintifice, EDP etc;
Procesarea semnalelor etc.
Este de doua feluri:directa si indirecta
Transformata Fourier -Proprietarily
TF are o serie de proprietati, cu ajutorul carora se pot determina TF ale multor functii comune:
Linearitate
TF a functiilor deplasate in timp la stanga sau la dreapta
TF a functiilor scalate in timp
Inversarea (semnului) timpului
Multiplicarea cu o putere a timpului t
Multiplicarea cu exponentiala frecventei- exp(jω0t)
Multiplicarea cu sinusul frecventei- sin(ω0t)
Multiplicarea cu cosinusul frecventei- cos(ω0t)
TF a derivatei unei functii in domeniul timp
Inmultirea in domeniul timp
Convolutia in domeniul timp
Proprietatea de dualitate
Teorema lui Parseval s.a.
C3
TRANSFORMATA LAPLACE (TL)
In analiza functionala, TL a unei functii original f(t) definita pentru t ≥ 0, este functia imagine F(s), definita de (TL directa):

Unde s = σ +iω este variabila complexa s, iar limita inferioara a integralei, adica 0- este notatia care reprezinta

si asigura incluziunea intregii functii Dirac delta, adica δ(t), in 0 (origine), daca acolo este un astfel de impuls in f(t), la 0.
Observatie; TL este numita astfel, in onoarea lui P-S Laplace (a utilizat-o in lucrarea sa despre teoria probabilitatilor), dar a fost descoperita de Leonhard Euler.
TL exista pentru toate numerele complexe care au Re>c,, unde c este o constanta reala, numita abscisa de convergenta. La TL bilaterala, deci limitele de integrare intre - ∞ si +∞, existenta acesteia (adica unde este ea definita), este intre limitele c < Re > d. Adica, valorile lui s pentru care exista TL, se numeste regiune de convergenta (RDC), sau domeniu de convergenta (DDC).
TL inversa este o integrala complexa tip Bromwich-Wagner
TL bilaterala este definita de relatia:

TRANSFORMATA LAPLACE (TL)
Legatura cu transformata Fourier
TF continua este echivalenta cu TL bilaterala
TRANSFORMATA LAPLACE (TL)
Proprietati si teoreme
Ca si TF, TL are o serie de proprietati si teoreme, cu ajutorul carora se pot determina TL directe sau inverse ale multor functii comune:
Linearitate
TL a functiilor deplasate in timp la dreapta (intarziere, retardare)
TL a functiilor cu timp scalat
Multiplicarea cu o putere a timpului t
Multiplicarea cu sinusul frecventei- sin(ω0t)
Multiplicarea cu cosinusul frecventei- cos(ω0t)
TL a derivatei unei functii in domeniul timp
TL a integralei unei functii in domeniul timp
Convolutia in domeniul timp
Teorema valorii (limita) initiale
Teorema valorii (limita) finale
Linearitate
![]()
Derivare (teorema derivarii)

Teorema integrarii in frecventa:

Teorema integrarii in timp:

Teorema valorii initiale:

Teorema valorii finale:
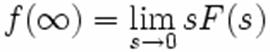
Teorema deplasarii in frecventa:

Teorema deplasarii in timp:

Teorema convolutiei:
![]()
Multiplicare cu o putere a timpului t:
![]()
Unde D este simbolul derivatei [aici, de ordinul n, a functiei F(s)]
TRANSFORMATE LAPLACE
rationale(i)
TL a unei functii, X(s), se zice este o functie rationala de s, daca poate fi scrisa ca un raport de polinoame in s, ireductibil, adica
X(s) = N(s)/D(s),
Unde N(s) si D(s) sunt polinoame in variabila complexa s, date de :
N(s) = bmsm + bm-1sm-1 +.+b1s + b0
D(s) = sn + an-1sn-1 +.+ a1s + a0,
puterile m si n fiind intregi pozitivi, iar coeficientii bm, bm-1,.,b1, b0 si an-1, an-2,, a1, a0 sunt numere reale
Polinomul D(s) se zice ca este monic, daca are coeficientul an, al lui sn, egal cu 1.
Intregul n, gradul lui D(s), se numeste ordinul functiei rationale X(s)
Daca n ≥ m, X(s) se zice ca este o functie rationala proprie.
Daca n > m, X(s) se zice ca este o functie rationala strict proprie
Radacinile polinomului D(s) (ecuatia D(s)=0), se numesc polii lui X(s)
Radacinile polinomului N(s) (ecuatia N(s)=0), se numesc zerourile lui X(s)
Daca TL X(s) a unei functii x(t) nu este o functie rationala, se zice ca este irationala. Adica, X(s) nu poate fi exprimata ca un raport de polinoame in s.
Exemplu: X(s) = e-t0s/s este irationala: exponentiala nu poate fi facuta un raport de polinoame
TRANSFORMATA Z (TZ)
generalitati
Transformata Z, in matematica, automatica, modelare, procesarea semnalelor etc., converteste un semnal din domeniul timp discret (deci o secventa de numere reale), intr-o reprezentare in domeniul frecventa complexa.
TRANSFORMATA Z
directa
TZ a unui semnal in timp discret z[n] este, prin definitie, functia imagine X(z), data (definita) de relatia (numita si TZ directa):

Unde n este un intreg, iar z este un numar circular complex de forma z = r ejω
TZ de mai sus, cu limitele sumei de la +la -∞, se mai numeste si TZ bilaterala, TZ pe ambele fete, TZ infinit dubla
TRANSFORMATA Z
inversa
TZ inversa este data de relatia de mai jos, unde C este un contur inchis antiorar ce incercuieste originea, intreaga regiune de convergenta (RDC) si toti polii lui X(z).

CALCULAREA T.F., T.L. SI T-Z IN MATLAB(i)
In Symbolic Math Toolbox (TL directa si inversa):
laplace calculeaza transformata Laplace directa a unei functii in t si rezulta o functie in s (cf. relatiei de definitie);
Exemplu:
>> syms t% arata ca orice variabila indicata va fi %utilizata simbolic si nu ca o valoare numerica
% aici, f(t) = t(functia original)
>> f = t
f =
t
>> laplace(f)
ans =
1/s^2
In Symbolic Math Toolbox (TL directa si inversa):
ilaplace - calculeaza transformata inversa Laplace a unei functii in s si rezulta o functie in t (cf. relatiei de definitie);
Exemplu:
>> syms s % arata ca orice variabila indicata va fi %utilizata simbolic si nu ca o valoare numerica
>> F=1/(s^2)
F =
1/s^2
>> ilaplace(F)
ans =
t
In Symbolic Math Toolbox (TF directa si inversa continua):
fourier(x)- calculeaza transformata Fourier directa a unei functii in timp continuu de x (variabila simbolica) si returneaza o functie in w (w = omega, deci, conform definitiei avem: f = f(x) ↔ F = F(w));
daca f = f(w), fourier returneaza o functie de t: F = F(t).
ifourier - calculeaza transformata inversa Fourier a unei functii in w si rezulta o functie in x (cf. relatiei de definitie: F = F(w) ↔ f = f(x)). Aici, x este o variabila simbolica, la fel t=timp;
daca functia F = F(x), ifourier returneaza o functie de t, adica: f = f(t)
In Symbolic Math Toolbox (Transformata z directa si inversa):
ztrans este transformata z directa a variabilei scalare simbolice in timp discret (de variabila independenta n), in functia imagine de z, F(z): f=f(n) ↔ F = F(z), conform cu comanda F = ztrans(f), respectiv relatia:
F(z) = f(n)/zn = f(n)*z-n
Exemplu:
>> syms n
>> F = 2^n*n
F =
2^n*n
>> ztrans(F)
ans =
1/2*z/(1/2*z-1)^2
In Symbolic Math Toolbox (Transformata z inversa):
iztrans este transformata z inversa, adica f = iztrans(F) a obiectului simbolic scalar F de variabila independenta z. Functia returnata este una de variabila independenta n, adica, f = iztrans(F)
Exemplu:
>> syms z
>> f = 2*z/(z-2)^2
f =
2*z/(z-2)^2
>> iztrans(f)
ans =
2^n*n
Exemplul 1 (Matlab-help). Sa se gaseasca componentele de frecventa ale unui semnal innecat(amestecat) cu un semnal zgomot, din domeniul timp. Se considera ca datele sunt esantionate la 1000 Hz.Semnalul contine componente de 50 Hz si 120 Hz si este amestecat cu zgomot aleator de medie zero.
>> zgomot aleator de medie zero: t = 0:0.001:0.6;
>> x = sin(2*pi*50*t)+sin(2*pi*120*t);
>> y = x + 2*randn(size(t));
>> plot(1000*t(1:50),y(1:50))
>> title('Semnal amestecat cu zgomot aleator de medie zero)
>> xlabel('timp (milisecunde)')
>> frequency axis: f = 1000*(0:256)/512;
>> plot(f,Pyy(1:257))
>> title(Continutul de frecvente a lui y')
>> xlabel(Frecventa (Hz)')
Identificarea componentelor de frecventa ale semnalului original contaminat cu zgomot nefiind posibila prin simpla inspectie cu privirea, convertim semnalul original (y) din domeniul timp, in domeniul frecventa (Y), utilizand TFR (FFT) in 512 puncte (comanda: Y = fft(y,512)). Spectrul de putere (puterile masurata la diverse frecvente/ armonice), se calculeaza cu: Pyy = Y* conj(Y) / 512. Spectrul de frecventa se observa pentru 256+1=257 puncte (restul de 255 nefiind necesare-redundanta)
>> Y = fft(y,512)
>> Pyy = Y* conj(Y) / 512
>> frequency axis: f = 1000*(0:256)/512;
>> plot(f,Pyy(1:257))
>> title(Continutul in frecventa al semnalului Y)
>> xlabel('frecventa [Hz]')
Exemplul 2. Calculul exact si aproximativ ale spectrului |F(ω)| (a TF adica), pentru functia impuls de ordinul 2, data de: f(t) = 1 pentru 0 ≤ t ≤ 2 si f(t) = 0, in rest (IIIb).
>> N = 128; % Aproximarea e mai buna daca se mareste N (256,512) si/sau se micsoreaza T
>> T == 0.1;
>> N = input( Input N: );
>> T = input(InputT: );
>> t = 0:T:2;
>> f = [ones(1, length(t))zeros(1,N-length(t))]
>> Fn = fft(f);
>> gam = 2*pi/N/T;
>> n = 0:10/gam;
>> Fapp = (1-exp(-j*n*gam*T))/j/n/gam*Fn;
>> w = 0:.05:10;
>> Fexact = 2*sin(w)./ww;
>> plot (n*gam,abs(Fapp(1:length(n))),og,w,abs(Fexact),b)
Examplul 3. Se da sirul / secventa x(n) = anu(n), 0 < |a| < ∞, secventa numita o secventa in timp pozitiv. Se cere sa se determine transformata Z a secventei utilizand Matlab.
% X(z) utilizand ztrans
% x(n) = a^nu(n)
>> x = 'a^n';
>> X = ztrans(x)
C4
(M.G.) 1. Scheme bloc (SB)
1.1 Probleme generale
SCHEMA BLOC F o interconectare de blocuri (subsisteme, simboluri) ce reprezinta, fiecare, operatii (functii) matematice, sau chiar MM, a.i., intreaga schema reprezinta MM al unui sistem.
Schemele bloc descriu parti componente ale unui sistem; ele ofera o modalitate de conectare si comportare directa cu EDO.
Un bloc indica legatura proportionala dintre transformatele Laplace a doua semnale I/E.
Functiile de proportionalitate se numesc functii de transfer sau transmitante.
F.d.t. (transmitantele) conecteaza semnalele de iesire (cauze) de cele de intrare (efecte), legatura fiind indicata printr-un bloc
Elementele SB
Schema bloc e o configuratie specifica de patru elemente:
Blocuri
Puncte de sumare
Puncte de ramificatie/ jonctiune (takeoff sau pickoff in Engleza)
Sageti, ce reprezinta curgerea unidirectionala a semnalului

Intelesul elementelor se observa din Fig.1; apoi:
Marimile (cantitatile, variabilele) originale din domeniul timpului, se noteaza cu litere mici. EXEMPLE: r = r(t); y = y(t) etc
Marimile (cantitatile, variabilele) imagini din domeniul variabilei complexe s care se utilizeaza la transformatele Laplace, se noteaza cu litere mari. EXEMPLE: R = R(s); C = C(s) etc
In schema bloc a unui SRA (Fig.2, v. mai jos): G1, G2, H sunt f.d.t: G1 = M/E, sau M = G1*E; H = Ym/Y etc

Fig.3 (a)-Element bloc; (b)-element de sumare(sumator);(c)- element/ punct de ramificatie/conexiune/jonctiune (takeoff-, pickoff point-LE)

LINIILE DE INTERCONECTARE A BLOCURILOR sunt variabilele ce descriu comportarea sistemului (cum sunt, de exemplu, variabilele I-S-E de la MM-SS).
Un sumator se utilizeaza pentru a arata adunarea sau scaderea (sumarea algebrica a) unor semnale. Poate avea oricate semnale de intrare, dar numai un singur semnal de iesire (Fig. 3-b). Semnele fiecarui semnal sunt utilizate langa varful sagetii semnalului respectiv.
Un punct de ramificatie (o conexiune sau un pickoff point), indica faptul ca acelasi semnal (ca valoare) pleaca spre/in mai multe locuri(Fig.3-c)
Un exemplu: Transmitanta (f.d.t.) a unui sistem de ord. 2:
EDO aferenta este: (d2y/dt2) + 2.5(dy/dt) + 18y = 3r, iar CI = 0 (conditiile initiale). Transmitanta (f.d.t.) este: T(s) = Y(s)/R(s)|CI = 0 = 3/ (s^2+2.5s+18). Ca urmare, blocul din Fig.4 contine transmitanta (f.d.t.).

Fig. 4: Transmitanta unui sistem de ordinul 2
SB ale SRA (ii) - forma canonica a SRA
Definitii (Fig. 5):
G = f.d.t. pe calea directa (f.d.t. directa)
H = f.d.t. pe calea inversa (f.d.t. de reactie)
GH = f.d.t. a buclei = f.d.t. a buclei deschise (open-loop)
Y/ R = f.d.t. a sistemului in raport cu intrarea; adica a buclei inchise (closed-loop)

F.d.t. ale elementelor SB
+/- = in relatiile de mai jos: sistem cu reactie negativa/ pozitiva
E/ R = raportul semnalului de actionare = raportul de transmisie al erorii (f.d.t. a erorii S- sensibilitate)
E/R = 1/ (1 GH)
Ym/ R = raportul de transmisie primar pe reactie (f.d.t. pe reactie; f.d.t. in raport cu iesirea; transmitanta in raport cu iesirea)
Ym/ R = GH / (1 GH)
Y/ R = f.d.t. a sistemului in circuit inchis (T- sensib. complementara)
Y/ R = G/ (1 GH)
Ecuatia caracteristica este (caracterizeaza comportarea dinamica):
(1 GH) = 0
Elemente ale SB - cand se utilizeaza?
Ipoteze de utilizare a modelelor grafice tip SB:
MG-SB se utilizeaza numai la subsisteme (blocuri) si/sau sisteme LTI;
Acestea nu contin elemente care stocheaza energie initiala
Din aceste motive se poate aplica transformarea Laplace
Rezulta ca fiecare bloc se poate reprezenta prin f.d.t. aferenta (vezi exemplul de mai sus).
Algebra schemelor bloc
Operatii in schemele bloc. Cum si cand?
Dupa ce sunt definite blocurile componente,
Dupa ce sunt identificate variabilele ce descriu comportarea acestuia
Dupa ce sunt obtinute tr. Laplace ale tuturor variabilelor si f.d.t.
Se definesc operatii si reguli de simplificare a schemelor bloc:
Sumarea variabilelor (in domeniile t sau s);
Multiplicarea variabilelor
Obtinerea functiilor de transfer a blocurilor cu diverse comportari:
Obtinerea functiilor de transfer a blocurilor cu diverse comportari:
P0( amplificator ideal);
P1(amplificator real);
I0(integrator ideal);
I1(integrator real);
Element cu Tm(timp mort=timp de intarzier pura);
PTm(element proportional cu timp mort);
PT1(proportonal cu intarziere de ordinul 1, sau, sistem de ordinul 1, sau, sistem aperiodic);
PT2(proportional cu intarziere de ordinul 2, sau sistem oscilant)
Conectarea in serie (in cascada) a blocurilor
Conectarea in paralel a blocurilor (subsistemelor)
Conectarea in bucla (sisteme cu reactie)
F.d.t. a sistemului inchis
Sisteme deschise, sisteme inchise
Mutarea din fata in spatele unui bloc a unui punct de conexiune.
Mutarea din spatele in fata unui bloc a unui punct de conexiune.
Mutarea din spatele in fata unui bloc a unui element sumator.
Mutarea din fata in spatele unui bloc a unui element sumator.
Rearanjarea SB ale sistemelor pentru a obtine structuri speciale ori pentru a efectua simplificari, ori f.d.t. echivalente etc., se numeste algebra schemelor bloc.
Deseori, manipularile furnizeaza intelegerea mai clara, mai adanca, a sistemului fizic si a comportarii acestuia.
Pentru sisteme SISO, reducerea schemei bloc inseamna simplificarea acestuia la un singur bloc, f.d.t. fiind una echivalenta pentru intregul sistem. Regulile de simplificare, usor de dedus, sunt:
Doua sau mai multe blocuri in serie (sau cascada), au f.d.t.(transmitanta) echivalenta egala cu produsul f.d.t. individuale ale blocurilor (Fig. 6-a)
Doua sau mai multe blocuri in paralel, au functia de transfer (transmitanta) echivalenta egala cu suma algebrica a f.d.t. individuale ale blocurilor (Fig. 6-b)
Fig.6: Echivalarea blocurilor conectate in serie (a) si in paralel (b)

La conexiunea (sau conectarea, configuratia) in bucla a doua blocuri (Fig. 7 de mai jos), sunt posibile doua semne la sumator (semnul reactiei). G(s) se numeste f.d.t. (transmitanta) de pe calea directa, iar H(s)-f.d.t. (transmitanta) de pe calea de reactie.

Legatura dintre semnalele I/E din Fig.7 se determina astfel:
Y(s) = G(s)E(s)
E(s) = R(s) H(s)Y(s)
Eliminand pe E(s) si obtinand pe Y(s) functie de R(s), avem:
Y(s) = G(s)[R(s) H(s)Y(s)] = G(s)R(s) G(s)H(s)Y(s),
de unde rezulta:
T(s) = Y(s)/R(s) = G(s)/[1 + G(s)H(s)]
Semnele minus ori plus pe reactie (adica reactie negativa ori pozitiva) dau semnele plus respectiv minus la numitorul f.d.t. a sistemului inchis
Reguli ce trebuie respectate la reducerea schemelor bloc sunt date mai jos:
Inserarea unei amplificari egale cu valoarea 1 (Fig. 8-a)
Schimbarea semnului unui semnal la un sumator(Fig. 8-b)
Mutarea unui punct de conexiune din spatele in fata unui bloc G1 (Fig. 8-c)
Mutarea unui punct de conexiune din fata in spatele unui bloc G2 (Fig. 8-d)
Combinarea a doua sau mai multe sumatoare (Fig.4-e)
Combinarea a doua sau mai multe puncte de conexiune (jonctiune, Fig.8-f)
Mutarea unui punct de conexiune din fata in spatele unui sumator (Fig. 8-g)
Mutarea unui punct de conexiune din spatele in fata unui sumator (Fig. 8-h)
8-a: Inserarea unui factor de amplificare unitar

Fig. 8-b: Schimbarea semnului unui semnal la un sumator

Fig. 8-c: Mutarea unui punct de conexiune din spatele in fata unui bloc [aici G1(s)]

Fig. 8-d: Mutarea unui punct de conexiune din fata in spatele unui bloc [aici G2(s)]

Fig. 8-e: Combinarea a doua sau mai multe sumatoare

Fig. 8-f: Combinarea a doua puncte de conexiune

Fig. 8-g: Mutarea unui punct de conexiune din spatele in fata unui sumator.

Fig. 8-h: Mutarea unui punct de conexiune din fata in spatele unui sumator.

Comenzile/ functiile series, parallel, feedback
Functia series:
Conecteaza in serie doua MM - LTI de orice tip (fdt, rss, zpk, frd), in timp continuu sau in timp discret (aici, trebuie sa aiba aceeasi perioada dec esantionare)
Sintaxa: sys = series(sys1,sys2)
Functia este echivalenta cu o inmultire directa: sys = sys1 * sys2
Functia parallel:
Conecteaza in paralel doua MM - LTI de orice tip (fdt, rss, zpk, frd), in timp continuu sau in timp discret (aici, trebuie sa aiba aceeasi perioada dec esantionare)
Sintaxa: sys = parallel(sys1,sys2)
Functia este echivalenta cu o adunare directa:sys = sys1 + sys2
Functia feedback:
Realizeaza conectarea in bucla inchisa (cu reactie) a doua MM - LTI de fdt, in timp continuu sau in timp discret (aici, trebuie sa aiba aceeasi perioada dec esantionare)
Sintaxa: sys = feedback(sys1,sys2)
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1050
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved