RENTABILITATEA SI RISCUL PORTOFOLIULUI

RENTABILITATEA SI RISCUL PORTOFOLIULUI[1]

Lichiditatea tot mai ridicata a titlurilor pe piata de capital permite combinarea lor in portofolii diversificate, in conformitate cu preferinta sau aversiunea fata de risc a oricarui investitor de capital. Evaluarea acestor portofolii se va face sub acelasi criteriu rentabilitate-risc.

Rentabilitatea anticipata pentru un portofoliu (speranta de rentabilitate a acestuia) este data de media rentabilitatilor anticipate (sperate) pentru titlurile din portofoliu. In consecinta, speranta de rentabilitate a portofoliului se va situa intre cea mai mica si cea mai mare rentabilitate individuala a titlurilor din respectivul portofoliu. Pentru un portofoliu format din doua titluri, rentabilitatea anticipata (E_p) va fi data de relatia:

unde:  E(R_i), E(R_j = rentabilitatile anticipate pentru cele doua titluri, i si j;

x, y = ponderile din capitalul total investit ale capitalurilor investite in titlurile i si j.

Riscul portofoliului (exprimat prin dispersia rentabilitatii) este o combinatie intre riscurile individuale ale titlurilor componente. Aceasta combinatie poate conduce (prin diversificare) la reduceri semnificative ale riscului total al portofoliului. Pentru un portofoliu format din numai doua titluri, dispersia rentabilitatii anticipate a portofoliului (σ²_p) va fi data de relatia:

unde: σ²_i, σ²_j = dispersiile rentabilitatilor anticipate pentru titlurile i si j, incluse in portofoliu;

σ_ij = covarianta intre rentabilitatile anticipate pentru titlurile i si j.

Aceasta combinatie depinde de marimea riscurilor individuale, de ponderile titlurilor in formarea portofoliului, dar si de marimea si sensul covariantei s_ij dintre rentabilitatile sperate ale titlurilor din portofoliu, respectiv de coeficientul de corelatie dintre aceste rentabilitati:

Astfel, un coeficient de corelatie egal cu unu (corelatie strict pozitiva, r_ij = 1) conduce la cel mai mare risc posibil al portofoliului ca medie ponderata a riscurilor individuale. Acest risc nu permite nici o imbunatatire a performantei portofoliului prin modificarea ponderilor din titlu.

Un coeficient de corelatie mai scazut (o < r_ij < 0,5) conduce la o ameliorare semnificativa a riscului portofoliului, ceea ce constituie in fapt situatia frecvent intalnita pe piata de capital. Aceasta caracteristica a riscului portofoliului este cea care motiveaza temeinic diferitele strategii active si pasive de gestiune a portofoliului.

O corelatie nula r_ij = 0) intre rentabilitatile unor titluri (teoretic) independente ar conduce, la limita (portofoliu echiponderat), la o reducere de 50% a riscului portofoliului. Mai mult, corelatia strict negativa (r_ij = - 1) poate conduce, intr-o anumita combinatie, la eliminarea totala a riscului portofoliului. Se recunoaste usor ca ambele situatii (r_ij = 0 si r_ij = - 1) sunt foarte, foarte rar intalnite pe piata de capital.

Cele mai frecvente sunt corelatiile pozitive si de slaba intensitate si asupra acestora se concentreaza preocuparile de gestiune eficienta a portofoliului. Practic, se urmaresc doua "tinte": 1) portofoliul cu varianta minima absoluta (PVMA, cu risc minim), pentru investitorii cu aversiune fata de risc, si 2) portofoliile eficiente care, la fiecare unitate de risc suplimentar asumata, asigura o crestere (maxim posibila) de rentabilitate sperata, pentru investitorii cu grade diferite de preferinta a riscului.

Speranta de rentabilitate a portofoliului se modifica numai in functie de ponderile x si y ale titlurilor componente.

Riscul portofoliului se modifica atat in functie de ponderile x si y, cat si de covarianta (coeficientul de corelatie) dintre rentabilitatile sperate ale titlurilor din portofoliu. Modificarea este neliniara si admite un punct de optim, respectiv, PVMA:

d/dx = 2x( +   - 2s_ij s_ij - )

Punctul de optim este posibil acolo unde derivata intai a riscului portofoliului in raport cu ponderea x este egala cu zero si in care aflam ponderea optima x* a primului titlu si, complementar, ponderea 1 - x* a celui de-al doilea titlu:

x*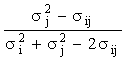

In acest punct de optim este situat portofoliul cu varianta minima absoluta (PVMA), care separa multimea portofoliilor posibile (din combinatiile x si y) in doua submultimi:

a) portofolii ineficiente, dominate, situate sub PVMA si care asociaza la fiecare crestere de risc de portofoliu o (atentie!) scadere de rentabilitate sperata

si

b) portofolii eficiente, dominante, situate deasupra PVMA si care asociaza la fiecare crestere de risc de portofoliu o crestere (neliniara) a rentabilitatii sperate.

Se delimiteaza astfel "frontiera eficienta" a tuturor portofoliilor eficiente posibile (inclusiv cel optim) intre PVMA si

In raport cu preferinta pentru risc, investitorul de capital va alege combinatia eficienta (portofoliul eficient) cu cea mai mare E_p* scontata. Toate celelalte combinatii posibile sau chiar titluri individuale detinute cu aceeasi speranta de rentabilitate (egala cu E_p*) vor fi insotite de riscuri mai mari si sunt deci ineficiente.

Reducerea riscului unui portofoliu se poate face pana la o limita a diversificarii (a combinarii) titlurilor, respectiv pana la riscul de piata ce caracterizeaza, in mod obiectiv, respectivul portofoliu:

bp = bi x* + bj (1-x*).

APLICATII REZOLVATE

1. Rentabilitatea si riscul portofoliului. Determinati rentabilitatea si riscul unui portofoliu format din trei titluri A, B si C, caracterizate prin:

Coeficientii de corelatie intre rentabilitatile celor trei titluri: r_AB r_AC r_BC

Rezolvare: Se aplica relatiile de determinare ale rentabilitatii si riscului portofoliului (exprimat prin dispersie) si se obtine:

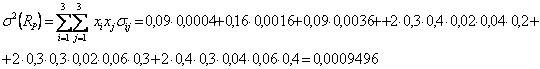
Riscul masurat prin abaterea medie patratica va fi:

2. Portofoliul de varianta minima absoluta (PVMA). Fie un portofoliu format din doua titluri, avand riscurile masurate prin abaterile medii patratice ale rentabilitatilor si = 4% si, respectiv, sj = 5%. Coeficientul de corelatie dintre rentabilitatile anticipate ale acestora este rij = 0,3. Determinati structura portofoliului de risc minim (de varianta minima).

Rezolvare: Fie x, respectiv (1 - x), ponderile asociate titlurilor i, respectiv, j.

Ponderea x*  a PVMA rezulta din rezolvarea ecuatiei:

(1)

unde:

(2)

Din rezolvarea ecuatiei (1) rezulta relatia de determinare a lui x*:

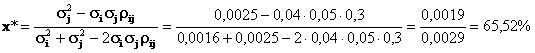
Asadar, portofoliul de varianta minima va avea in compozitie 65,52% din titlul i si 34,48% din titlul j.

Problema nr.3. Rentabilitatea si riscul portofoliilor. Pe o piata financiara sunt cotate trei valori mobiliare caracterizate prin urmatorii indicatori de performanta:

Coeficientii de corelatie dintre rentabilitatile celor trei titluri sunt: r (Ra, Rb) = 0,3; r (Ra, Rc) = 0,5; r (Rb, Rc) = - 0,2. Determinati:

a)      rentabilitatea si riscul portofoliului pietei;

b)      rentabilitatea si riscul portofoliului de varianta minima.

Rezolvare: (a) Structura portofoliului pietei este determinata de ponderile capitalizarilor bursiere ale fiecarui titlu in capitalizarea bursiera a pietei bursiere,deci de:

Pentru a determina rentabilitatea si riscul acestui portofoliu se vor aplica relatiile (1) si (2), rezultand:

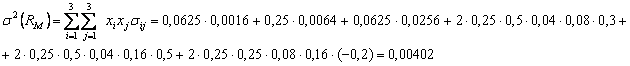s (R_M) = 6,34034%.

(b) Pentru a determina portofoliul de risc minim (PVMA) trebuie calculate derivatele partiale ale dispersiei portofoliului in functie de ponderile celor trei titluri, avand in vedere ca suma ponderilor trebuie sa fie egala cu 100%.

Se vor calcula derivatele functiei lui Lagrange :

in functie de necunoscutele x_i (cu i=a,b,c) si l

Un calcul simplificat are in vedere ca: , calculandu-se numai doua

derivate, in functie de x_a si x_b.

Din derivarea relatiei (2) in functie de x_a si x_b rezulta un sistem de doua ecuatii cu doua necunoscute:

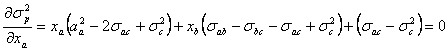
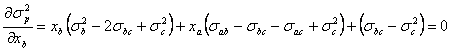
Inlocuind cu datele numerice ale problemei, rezulta sistemul:

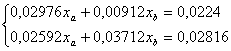
Solutiile acestui sistem sunt:

x_a = 66,17528%

x_b = 29,67434%

x_c = 4,15038%.

Rentabilitatea si riscul acestui portofoliu vor rezulta prin aplicarea relatiilor (1) si (2):

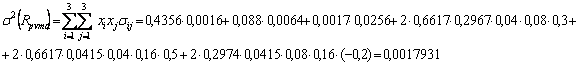
s(R_pvma) = 4,2345%.

REFERINTE BIBLIOGRAFICE