Exercitii si probleme propuse - statistica

Exercitii si probleme propuse

1. Fie caracteristica X, care are distributia empirica de selectie

Se cere:

a) media de selectie, momentul centrat de selectie de ordinul doi si dispersia de selectie;

b) functia de repartitie de selectie.

Raspunsuri. a)

b)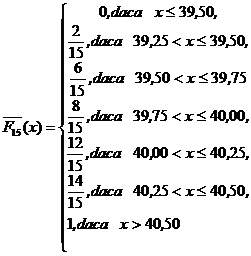

In urma unei selectii de volum n=100, privind caracteristica X, s-au obtinut urmatoarele date de selectie :

Se cere:

a) o estimatie absolut corecta pentru media teoretica m=M(X),

b) o estimatie corecta si una absolut corecta pentru dispersia teoretica

Raspunsuri. a) =10,65; b)

3. Fie caracteristica X , care are distributia teoretica

unde pI(0,1) este necunoscut.

Se considera o selectie repetata de volum n, relativa la caracteristica X.

Sa se arate ca functia de selectie

este o functie de estimatie nedeplasata pentru p².

Raspuns .

4. Fie caracteristica X, ce urmeaza legea lui Poisson, cu parametrul necunoscut. Se considera o selectie repetata de volum n.

Se cere

a) estimatorul de verosimilitate maxima pentru parametrul

b) sa se arate ca este estimator absolut corect pentru

c) sa se determine ca este estimator eficient pentru

Raspunsuri a) ; b) M( , D²(

c) I( , D²(

Relativ la populatia C, se cerceteaza caracteristica X ce urmeaza legea normala N(m,d cu media teoretica m=M(x) necunoscuta si dispersia d =0,006. Sa se determine intervalul de incredere pentru m, cu probabilitatea de incredere 1-a=0,9, daca se cunosc datele de selectie.

10,5 10,8 11,2 10,9 10,14 10,6 10,9 11,0 10,3 10,8 10,6 11,3 10,5 10,7 10,8 10,9 10,8 10,7 10,9 11,0

Raspuns. Z_1-a

mI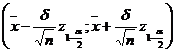

6. Se efectueaza 12 masuratori independente asupra caracteristicii X, rezultatele obtinute dand distributia empirica de selectie

Folosind probabilitatea de incredere 0,95 sa se determine intervalul de incredere pentru valoarea medie teorerica m=M(X).

Raspunsuri t_11,1-a

mI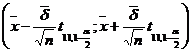

Caracteristicile X′ si X′′ relative la doua populatii independente, urmeaza fiecare legea normala, respectiv N(m′,d si N(m′′,d′′), unde d si d′′=0,004 Relativ la aceste caracteristici s-au obtinut urmatoarele date selectie:

X 0,240, 0,240, 0,235, 0,25, 0, 235;

X

Folosind probabilitatea de incredere 0,98, sa se determine intervalul de incredere pentru diferenta m′-m′′

Raspuns. z_1-a =2,33, m′-m"I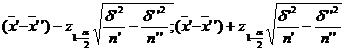

8. Cu datele problemei precedente, dar d d d necunoscut, sa se determine intervalul de incredere pentru diferenta m′-m′′

Raspuns t_8;1-a

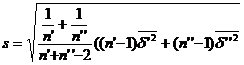
m′-m′′I

9. Caracteristica X urmeaza legea normala N(m,d). Se considera o selectie repetata de volum n=15 relativa la X cu datele de selectie

Sa se determine intervalul de incredere pentru dispersia d =D²(X) si pentru abaterea standard d, folosind probabilitatea de incredere 0,9.

Raspuns

d I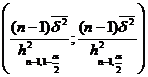

d I

10. Caracteristica X reprezinta media obtinuta de un student care a promovat anul I de studii. Sa se verifice, cu nivelul de semnificatie a=0,05, ipoteza ca media teoretica m=M(X)=7,25, daca se considera ca d =1,5, si s-a facut un sondaj de volum n 42, pentru care s-au obtinut datele de selectie:

Raspuns z_1-a =1,96 , z= I(-1,96; 1,96), ipoteza m=7,25 este admisa.

11. Caracteristica X reprezinta rezistenta la rupere a cablurilor produse de o anumita fabrica. Considerand ca X urmeaza legea de probabilitate normala N(m,d), sa se verifice, folosind nivelul de semnificatie a=0,05, ipoteza ca media teoretica a rezistentei la rupere a cablurilor este de 400Kg , daca se dispune de o selectie de volum n=10, cu urmatoarele date de selectie

401,403,398,98,400,5,399,396,401,5,400,5,398,

Raspuns t_n-1,1-a =2,262 , t= I(-2,262; 2,262), ipoteza m=400 este admisa

12. Doua masini produc piese de acelasi tip.Fie X′ dimensiunea pieselor produse de prima masina, respectiv X′′sa fie dimensiunea pieselor produse de a doua masina, fiecare urmand legea normala, respectiv N(m′,0,02) si N(m′′,0,15). Sa se verifice, folosind nivelul de semnificatie a=0,05, ipoteza ca mediile dimensiunilor pieselor (in mm) produse de cele doua masini sunt egale, cu alternativa ca ele difera, daca se dispune de selectiile, care au ca distributii empirice de selectie, respectiv

,

Raspuns. Z_1-a z=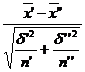

Ipoteza m′=m′′ este respinsa.

Doua masini produc acelasi tip de articol. Se efectueaza doua selectii de volume n′=12 si n′′=15 si se masoara dimensiunea produselor, datele de selectie sunt trecute in tabelele urmatoare

x′_k 3,5 3,6 3,7 3,8 x′_k 3,4 3,6 3,8

f′_k 3 4 2 3 f′_k 2 4 9

Considerand nivelul de semnificatie a=0,01, sa se verifice ipoteza ca mediile dimensiunilor articolelor produse de cele doua masini nu difera semnificativ, stiind ca dispersiile teoretice pentru cele doua caracteristici coincid.

Raspuns t_25,1-a

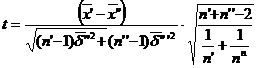I

ipoteza m′=m′′ este admisa.

14. Se cerceteaza caracteristica X ce reprezinta diametrul pieselor produse de o masina (in mm). Stiind ca X urmeaza legea normala N(m,d) si avand o seleciie de volum n=11, care ne da distributia empirica de selectie

sa se verifice ipoteza nula

H d =0,003, cu alternativa H₁: d

cu nivelul de semnificatie a

Raspuns h²_n-1,a =2,16 , h²_n-1,1-a

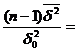h²= I(-2,16;20,5), ipoteza d =0,003 este admisa.

1 Se cerceteaza aceeasi caracteristica pentru doua populatii independente, care este respectiv X′ pentru prima populatie si X′′ pentru a doua, fiecare urmand legea normala N(m′, s′) si N(m′′, s′′). Se considera selectiile de volum n si n′′= 12, care ne dau distributiile empirice de selectie.

Considerand nivelul de semnificatie a ′ 0,02 sa se compare dispersiile celor doua populatii.

Raspuns. 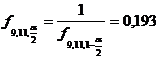, ipoteza s s′′² este admisa.

16. Pentru a cerceta daca durata de ardere a doua loturi de becuri este aceeasi s-a luat cate un esantion de 20 de becuri din fiecare lot, care au fost incarcate in privinta caracteristicii studiate si s-au obtinut urmatoarele rezultate:

1110, 1050, 1090, 1140, 1130, 1240, 1010, 1110, 1100,

ore de ardere pentru esantionul din primul lot si respectiv:

ore de ardere pentru esantionul din al doilea lot.

a) Folosind nivelul de semnificatie a= 0,01, sa se verifice daca dispersiile pentru cele doua loturi nu difera semnificativ.

b) Folosind nivelul de semnificatie a= 0,05, si rezultatul de la punctul precedent , sa se verifice daca duratele medii de ardere pentru cele doua loturi sunt aceleasi.

Raspunsuri: a)

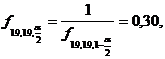
, ipoteza s s′′ este admisa

b)

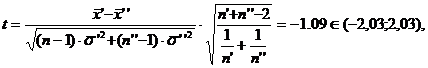
ipoteza m′=m′′ este admisa

.Se considera caracteristica X ce reprezinta greutatea in grame a unor cutii incarcate automat de un dispozitiv. Pentru verificarea normalitatii lui X, se considera o selectie de volum n=100, datele de selectie fiind urmatoarele:

Se cere :

a) aplicarea testului X², cu nivelul de semnificatie a=0,05, pentru verificarea normalitatii luiX,

b) aplicarea testului lui Kolmogorov, cu nivelul de semnificatie a=0,05 , pentru verificarea normalitatii lui X.

Raspunsuri ;

a), ipoteza normalitatii este admisa.

b)ipoteza normalitatii este acceptata.

Se considera caracteristica X ce reprezinta durata unei convorbiri telefonice interurbane (in minute). Pentru cercetarea duratei convorbirilor interurbane se considera o selectie de volum n= 200, datele de selectie obtinute sunt trecute in tabelul urmator :

Sa se verifice exponentialitatea lui X, cu nivelul a=0,005 de semnificatie, folosind:

a) testul χ²,

b) testul lui Kolomogorov.

Raspunsuri 0,12415,

a) h²_4;1-a =9,48<60,4985=h²=, ipoteza exponentialitatii este respinsa.

b) 0,1752=2,48>x_1-a=1,36, ipoteza exponentialitatii este respinsa.