Testarea ipotezelor statistice - demersul testarii unei ipoteze statistice, concepte si erori in testarea ipotezelor statistice, teste de concordanta

TESTAREA IPOTEZELOR STATISTICE

1. DEMERSUL TESTARII UNEI IPOTEZE STATISTICE.

Demersul testarii unei ipoteze presupune parcurgerea unor etape si rezolvarea problemelor pe care le implica, si anume18:

     Se formuleaza ipotezele, in functie de problema pusa;

     Se alege un test statistic in functie de distributia de selectie a statisticii considerate;

     Se alege un prag de semnificatie pentru test;

     Se stabilesc regulile de decizie, definind regiunile de acceptare si de respingere a ipotezei H₀;

     Se calculeaza valoarea statisticii test, folosind datele inregistrate prin sondaj;

     Se compara valoarea calculata a statisticii test cu valoarea teoretica;

     Se ia decizia de a nu respinge sau de a respinge ipoteza admisa.

In urma extragerii unui esantion dintr-o populatie statistica prin prelucrarea datelor provenite din sondaj se obtine un estimator al parametrului urmarit in populatia de origine. Problema care se pune este in ce masura parametrul estimat pe baza rezultatelor sondajului asigura credibilitatea aprecierilor facute asupra intregii colectivitati.

Estimatorul este, o presupunere a parametrului, adica, o ipoteza statistica.

Definitie: Se numeste ipoteza statistica ipoteza care se face cu privire la parametrul unei repartitii sau la legea de repartitie pe care pe care o urmeaza variabilele aleatoare.

Ipoteze statistice:

o      Ipoteza nula;

o      Ipoteza alternativa.

In toate domeniile stiintelor aplicate este necesar sa se recurga la experimentarea unor noi metode, tehnologii, produse, facandu-se presupuneri asupra superioritatii lor fata de procedeele curent folosite in vederea luarii unei anumite decizii. Totodata este necesar sa verificam daca in timp s-au produs modificari in ceea ce priveste parametrii populatiei sau exista diferente semnificative intre diferite grupuri ale aceleiasi populatii. Toate aceste presupuneri constituie niste ipoteze a caror valabilitate trebuie verificata si deoarece aceasta verificare se face statistic (operandu-se cu date obtinute in urma unei selectii statistice dintr-o populatie) ele se denumesc ipoteze statistice.

Verificarea concordantei rezultatelor experientei cu una dintre ipoteze se face pe baza unui criteriu statistic furnizat de un ansamblu de reguli de prelucrare a datelor numit test statistic. Cu ajutorul lui se ajunge la decizia de a respinge o ipoteza si a accepta alta. Luarea unei decizii cu privire la o ipoteza statistica se numeste testarea ipotezei.

O ipoteza se numeste simpla daca ea determina in mod univoc repartitia specificata a variabilei aleatoare si compusa daca este formata dintr-un numar finit de ipoteze simple.

Testele statistice furnizeaza criterii pe baza carora se accepta sau se respinge o ipoteza cu privire la o populatie statistica pe baza observatiilor facute intr-un esantion aleator extras din ea.

Alegerea testului nu depinde de esantion, de aceea procedeul de testare a ipotezei si ipoteza se pot specifica inainte de selectie.

Trebuie subliniat faptul ca printr-un test statistic nu se stabileste adevarul ci doar daca rezultatele selectiei sprijina ipoteza formulata si cu ce probabilitate.

2. CONCEPTE SI ERORI IN TESTAREA IPOTEZELOR STATISTICE

In statistica, ipotezele apar intotdeauna in perechi: ipoteza nula si ipoteza alternativa.

Ipoteza statistica ce urmeaza a fi testata se numeste ipoteza nula si se noteaza H₀

Ea consta intotdeauna in admiterea caracterului intamplator al deosebirilor, adica in presupunerea ca nu exista deosebiri esentiale.

Respingerea ipotezei nule implica acceptarea unei alte ipoteze numita alternativa, notata cu H₁.

Definitie: Procedeul de verificare a unei ipoteze statistice se numeste test sau criteriu de semnificatie.

Verificarea ipotezei nule se face pe baza unui esantion de volum n, extras din populatia X. Daca punctul definit de vectorul de sondaj x₁, x₂, , x_n cade in regiunea critica R_c, ipoteza H₀ se respinge, iar daca cade in afara regiunii critice R_c, ipoteza H₀ se accepta

Eroarea pe care o facem eliminand o ipoteza nula, desi este adevarata se numeste eroare de genul intai.

Probabilitatea comiterii unei astfel de erori reprezinta riscul de genul intai (α) si se numeste nivel sau prag de semnificatie.

Nivelul de incredere al unui test statistic este (1- α), iar (1- α)100 reprezinta probabilitatea de garantare a rezultatelor.

Eroarea pe care o facem acceptand o ipoteza nula, desi este falsa se numeste eroare de genul al doilea, iar probabilitatea (riscul) comiterii unei astfel de erori se noteaza cu β. Puterea testului statistic este (1- β).

Erorile de tip I pot fi micsorate de cercetator fixand nivelul de semnificatie α cat mai mic. Erorile de tip II pot fi micsorate prin cresterea volumului esantionului. Daca variatia selectiei este mai mica se reduc ambele erori.

Deoarece evitarea unui tip de eroare sporeste sansa celeilalte devine important de stiut care tip de eroare trebuie mai atent evitat.

3. TESTE DE CONCORDANTA

Acest subcapitol se refera la concordanta, potrivirea dintre valorile calculate in esantion si valorile parametrilor din colectivitatea generala.

Testele de concordanta se mai numesc teste de ajustare, care exprima potrivirea unei distributii empirice la o distributie asteptata sau teoretica.

Fie populatia de interes, notata cu P₁. pentru orice esantion se poate considera o populatie de baza, P₂, din care esantionul va fi extras.

Problema este daca se poate considera ca P₂ concorda cu P₁. ipoteza nula va afirma ca P₁ si P₂ concorda. Respingerea ipotezei nule va avea in practica doua consecinte:

se va considera ca esantionul nu este reprezentativ pentru populatia de interes, populatie considerata stabila si se va extrage un alt esantion

se va considera ca populatia P₁ s-a schimbat, noua populatie de referinta este P₂.

3.1. Eroarea standard estimata a mediei

In testul erorii standard al mediei, se presupune ca sunt indeplinite conditiile care asigura mediei de sondaj o repartitie normala (esantion n30) sau aproape normala. De aceea variabila aleatoare z urmeaza o distributie normala standard (z este variabila normala normata).

Eroarea standard:

     Este un indice pentru variabilitatea mediilor in cazul mai multor esantioane extrase din populatie; ea este media masurii cu care media esantioanelor difera fata de media populatiei din care au fost extrase;

     Este folosita in cea mai mare parte ca un pas intermediar in alte tehnici statistice (cum ar fi testul t);

     La fel ca si abaterea standard si variatia poate fi folosita ca un indice pentru variabilitatea scorurilor unei variabile;

3.2. Compararea a doua esantioane de scoruri corelate/relationate. (Testul t)

Testul este publicat in 1908 de W.S. Gosset sub pseudonimul Student. Principala diferenta intre distributiile de esantionare ale statisticilor z si t este aceea ca distributia t are o cantitate de variabilitate mai mare decat z.

Testul t:

         Este folosit pentru evaluarea semnificatiei statistice a diferentei dintre mediile pentru doua seturi de scoruri; ele ajuta la elucidarea intrebarilor comune ale cercetatorilor daca valoarea medie pentru un set de scoruri difera de valoarea medie pentru alt set de scoruri;

Deoarece, in cercetare, in mod invariabil, se lucreaza cu esantioane de oameni extrase din populatia latenta, trebie sa estimam daca orice diferenta pe care o obtinem intre cele doua seturi de valori este semnificativa statistic.

Exista doua variante ale testului t:

1. Pentru esantioane perechi

- folosit cand cele doua seturi de scoruri ce trebuie comparate provin dintr-un singur esantion;

- cand coeficientul de corelatie intre cele doua seturi este mare.

Uneori ne lovim de situatii in care esantioanele din care provin mediile ce trebuie comparate sunt dependente (procedeul de selectie al unui esantion este legat de procedeul de selectie al celuilalt).

Cand elementele celor doua esantioane sunt asociate intr-un anumit mod doua cate doua (de exemplu: rezultatele inregistrate inainte si dupa actiunea unui factor experimental), procedeul cel mai simplu consta in a rationa asupra diferentelorpe care le prezinta fiecare pereche de date asociate, corelate.

2. Pentru esantioane independente

- se foloseste cand cele doua seturi de valori provin din grupuri diferite de participanti, pentru a calcula daca mediile acestora sunt diferite semnificativ una fata de cealalta.

In cazul esantioanelor independente, probele de semnificatie difera in functie de doua situatii:

Cand numarul de masuratori (N) in fiecare esantion este destul de mate (mai mare ca 30);

Cand numarul de masuratori sau volumul esantionului este mai mic deact 30.

3.3. Testul Chi-square

(Diferente intre frecventele esantioanelor)

In general, testul chi-square este folosit pentru evaluarea existentei unei diferente semnificative intre doua sau mai multe esantioane care sunt formate din date de frecventa (date nominale). Altfel spus, este testul statistic uzual care analizeaza tabelele de asociere sau contingenta pe baza a doua variabile categoriale nominale.

De asemenea, poate fi folosit si pentru testarea faptului ca un singur esantion este semnificativ diferit fata de o populatie cunoscuta.

Observatie: Aceasta aplicatie este cea mai putin comuna, deoarece caracteristicile unei populatii snt rareori cunoscute in cercetare.

Observatie: Trebuie avut in vedere faptul ca o analiza chi-square trebuie sa includa datele fiecarui individ o singura data. Frecventele totale trebuie sa fie egale cu numarul de persoane folosite in analiza.

3.4. Testul Z pentru esantioane independente, dispersii cunoscute

Cand am discutat de abaterea standard, am vazut ca aceasta reprezinta um mijloc de raportare a modului in care rezultatele se imprastie in jurul ei. De asemenea, am spus ca, daca cunoastem media si abaterea standard, putem foarte usor sa precizam probabilitatea ca un scor para se situeze intr-o anumita pozitie. Pentru disciplinele socio-umane, acest lucru este vital, deoarece atunci cand masuram, practic precizam pozitia pe care o are un subiect in raport cu o populatie de referinta.

Este ideal ca aceasta pozitie sa poata fi prezentata intr-o maniera standardizata. Acest lucru poate fi usor de indeplinit daca avem in vedere conceptual de note standardizate.

La baza acestui concept stau notele z. Notele z reprezinta diferenta dintre scorul observat si medie, in termeni de abatere standard, cu alte cuvinte, notele z nu sunt altceva decat distantele la care se situeaza scorurile particulare in raport cu media grupului iar aceasta distanta este exprimata standardizat.

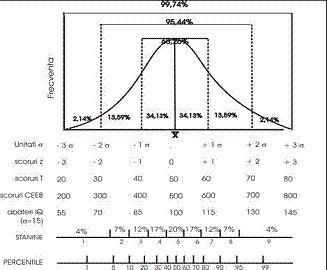
Teoretic, notele z sunt note obtinute pe o curba cu media 0 si abaterea standard 1. In acest caz, o distributie normala are practic notele z cuprinse intre -3 si +3, intre aceste note regasindu-se peste 99% din populatie, dupa cum observati in figura de alaturi.

Multe cazuri de analiza statistica implica o comparatie intre mediile a doua colectivitati generale.

Exemplu: Un patron al unui restaurant doreste sa vada daca exista diferente intre vanzarile realizate inainte si dupa o campanie de publicitate;

Exemplu: Un grup de consumatori doreste sa vada daca exista o diferenta semnificativa intre consumul electric pentru doua tipuri de cuptoare cu microunde.

Notele z au si ele o serie de proprietati cu aplicabilitate practica de-osebita, dintre care:

Media unei distributii z este egala cu zero, afirmatie ce rezulta din proprietatea acestui indicator de a se diminua atunci cand scadem o constanta din fiecare scor particular. Deoarece din formula rezulta aceasta diferenta (se scade fiecare scor particular din medie), in final media va ajunge la valoarea zero;

Abaterea standard a unei distributii z este intotdeauna 1. Si aceasta afirmatie rezulta din proprietatile abaterii standard. Stim ca daca impartim abaterea standard la o constanta, valoarea acesteia se divide corespunzator. Din formula, observam ca acea constanta la care impartim este chiar abaterea standard iar impartirea a doua numere egale are ca rezultat 1.

Notele z sunt note direct calculabile, utilizandu-se media si abaterea standard si reprezinta temelia oricarui proces de standardizare.

	4. Alegeti raspunsul corect

1. Un estimator statistic reprezinta:

a. o functie de variabile aleatoare de selectie, independente si identic distribuite;

b. o valoarea tipica de sondaj;

c. o estimatie a parametrului populatiei.

2. Valoarea medie calculata la nivelul unei populatii reprezinta:

a. un parametru;

b. o valoare tipica de sondaj;

c. un estimator;

d. o estimatie.

3. Eroarea limita este folosita la stabilirea:

a. preciziei unei estimatii;

b. unei variabile independente;

c. intervalului de variatie a mediei de selectie fata de media generala.

4. Intr-un proces de testare a ipotezelor statistice, eroarea de genul intai este:

a) eroarea pe care o facem acceptand ipoteza nula cand ea este adevarata;

b) eroarea pe acre o facem acceptand ipoteza nula atunci cand ea este falsa;

c) eroarea pe care o facem acceptand ipoteza alternativa cand ea este adevarata;

d) eroarea pe care o facem eliminand ipoteza nula atunci cand ea este adevarata;

e) eroarea pe care o facem eliminand ipoteza alternativa atunci cand ea este adevarata.

5. Intr-un proces de testare a ipotezelor statistice, eroarea de genul al doilea este

a)     eroarea pe care o facem acceptand ipoteza nula cand ea este adevarata;

b)     eroarea pe care o facem acceptand ipoteza alternativa cand ea este falsa;

c)     eroarea pe care o facem acceptand ipoteza nula cand ea este falsa;

d)     eroarea pe care o facem eliminand ipoteza nula cand ea este adevarata;

e)     eroarea pe care o facem eliminand ipoteza alternativa atunci cand ea este falsa.

6. Marimea intervalului de incredere al unui parametru creste o data cu scaderea:

a. volumului esantionului;

b. coeficientului de incredere ;

c. variantei populatiei.

7. Testul t este folosit pentru:

a. evaluarea semnificatiei statistice a diferentei dintre mediile pentru doua seturi de scoruri;

b. evaluarea existentei unei diferente semnificative intre doua sau mai multe esantioane

c. testarea faptului ca un singur esantion este semnificativ diferit fata de o populatie cunoscuta.

8. Testul chi square este folosit pentru:

a. evaluarea semnificatiei statistice a diferentei dintre mediile pentru doua seturi de scoruri;

b. evaluarea existentei unei diferente semnificative intre doua sau mai multe esantioane

c. testarea esantioanelor independente.

9. Testul t se poate folosi pentru:

a. testarea ipotezelor statistice cu privire la parametrii unui model;

b. testarea normalitatii unei distributii;

c. testarea inegalitatii a doua medii.

10. Testarea mediei unei distributii se poate realiza folosind:

a. testul chi.square;

b. testul t student;

c. histograma.

11. Pentru testarea egalitatii a doua medii se foloseste:

a. testul t student;

b. Testul chi-square;

c. testul fisher.

	5. Raspunsuri corecte

1. a. o functie de variabile aleatoare de selectie, independente si identic distribuite;

2. a. un parametru;

3. c. intervalului de variatie a mediei de selectie fata de media generala;

4. d. eroarea pe care o facem eliminand ipoteza nula atunci cand ea este adevarata;

5. c. eroarea pe care o facem acceptand ipoteza nula cand ea este falsa;

6. a. volumului esantionului;

7. a. evaluarea semnificatiei statistice a diferentei dintre mediile pentru doua seturi de scoruri;

8. b. evaluarea existentei unei diferente semnificative intre doua sau mai multe

esantioane

9. a. testarea ipotezelor statistice cu privire la parametrii unui model;

10. b. testul t student;

11. a. testul t student;