PROBABILITATI SI STATISTICA

PROBABILITATI SI STATISTICA

1. Camp de evenimente

1.1 Introducere

Teoria probabilitatilor este o stiinta a naturii, o stiinta matematizata, intr-ucat urmareste constructia de modele matematice. In teoria probabilitatilor, obiectul central este un sistem de elemente ale unor procese, procese in care realizarile nu sunt previzibile si se reprezinta matematic ca elemente aleatoare, carora li se pot asocia probabilitati.

Teoria matematica da sistemului de evenimente, care corespund unui eveniment, o reprezentare sprijinita pe teoria multimilor. Fiecare rezultat este o parte a unei multimi, rezultatele posibile ale experimentului sunt diferite partiale acestei multimi, legate intre ele prin relatile logice "sau", "si", "non".

In teoria probabilitatilor, notiunea de eveniment este o notiune primara, si se considera dintr-un singur punct de vedere, acela de produceri sau neproduceri in decursul unui eveniment.

1.2 Definitii

Def 1

Evenimentul contrar lui A, sau non A, este evenimentul care se produce atunci si numai atunci cand nu se produce evenimentul A. Notatie: - complementa lui .

Def 2

Evenimentul, sau A sau B, (sau reuniunea evenimentului A si B), este evenimentul care se produce atunci si numai atunci cand se produce cel putin unul din evenimentele A, B. Notatie: (A reunit cu B).

Def 3

Evenimentul, si A si B, sau intersectia evenimentelor A si B, este evenimentul care se produce atunci si numai atunci cand se produc ambele evenimente A si B. Notatie: (A intersectat cu B).

Observatii:

AUC_A = Ω A∩C_A = Ø

Evenimentul Ω este evenimentul sigur. Evenimentul cu Ø este evenimentul imposibil.

Def 4

Se spune ca evenimentul A si B sunt incompatibile daca A∩B= Ø

Def 5

Spunem ca evenimentul A implica evenimentul B daca producandu-se A, in mod necesar se produce si B. Notatia: AB.

Def 6

Se numeste partitie sau desfacere finita a unei multimi Ω, o familie finita de submultimi a lui Ω disjuncte doua cate doua, si a carei reuniniune este Ω.

Def 7

Un corp K generat de o desfacere a unei multimi Ω este format din elementele desfacerii din multimea vida, si din toate reuniunile posibile ale elementelor desfaceri.

Exemplu: delta ;

; ;

; ;

- multimea partilor lui Ω

Def 8

Prin camp de evenimente intelegem un cuplu (Ω,K), unde K este un corp generat de o desfacere a multimii omega.

Def 9

Elementele desfacerii care genereaza corpul K, se numesc evenimente elementare ale campului de evenimente (Ω,K).

Def 10

Elementele corpului K se numesc evenimente ale campului (Ω,K).

Observatii: Un camp finit de evenimente este complet determinat de multimea evenimentelor sale elementare. Orice element al campului este o reuniune de evenimente elementare.

2. Camp de probabilitate

2.1 Definitia axiomatica a probabilitatii.

Fie (Ω,K) un camp de evenimente;    Ω - multimea evenimentelor elementare

Def :

O probabilitate P pe campul de evenimente (Ω,K) este o functie definita pe K cu valori in R, (P: K→R), care satisface urmatoarele proprietati:

1). (Axiomele lui Kolmogorov)

2).

3). pentru orice 2 evenimente incompatibile

Observatie:

Proprietatea 3 se extinde pentru orice familie finita de evenimente incompatibile 2 cate 2.

Def :

Un camp de evenimente (Ω,K), inzestrat cu o probabilitate P se numeste camp de probabilitate. Notatie: (Ω,K,P)

2.2 Consecinte din definitia axiomatica a probabilitatilor.
a)    

Din si Þ in baza proprietatii axiomei 3 si 2 ca: Þ conf. probabilitatii axiomei 2 ca: Þ .

b) (complementara lui omega). Din a) Þ conf. prop. 2.

c)     Þ Þ

d)     ,

Din     , Þ , Þ

e) e- se extinde pentru numar finit de evenimente in felul urmator:

f)

Exemplu:

2.3 Alte definitii ale probabilitatilor.

Sa presupunem ca Ω este o multime finita. . cu

daca

Daca mai facem in plus si ipoteza ca evenimentele elementare sunt egal probabile, adica atunci Þ

Þ

Considerand acum un eveniment arbitrar

Am ajuns astfel la definitia clasica a unui eveniment, ca fiind raportul dintre numarul de evenimente elementare egal probabile , favorabile evenimentului considerat, si numarul total de evenimente elementare egal probabile.

Experiment:

Aruncare cu zarul.

evenimente elementare.

A = aparitia unei fete impare A = Þ k=3 (nr. cazurilor favorabile) si n=6.

Cazuri favorabile (k). Nr cazurilor egal posibile (n)

Definitia Statistica:

Sa consideram experimentul "aruncarea cu banul". S,B,B,S,B,S,B..(Stema, Ban).

Nu putem prevedea ce va aparea la urmatoarea aruncare. Un rezultat final insa, poate fi prevazut:

La 1000 de aruncari de 500 ori stema, de 500 de ori banul. Buffon - 4000 de aruncari a obtinut P=0,5069, Parson 24000 de aruncari a obtinut P=0,5005. Sa presupunem ca la 1000 de aruncari obtinem banul de 488 de ori. m=488. Acest numar poarta numele de frecventa absoluta a aparitiei banului. Acesta este un rezultat statistic.

Frecventa relativa este raportul unde n - este numarul aruncarilor(numar de repetari ale experimentului).

Frecventa relativa devine stabila la un numar mare de incercari . Valoarea teoretica a acestei frecvente este probabilitatea evenimentului considerat, si aceasta constituie definitia statistica a probabilitatii.

Definitia Geometrica

S

Consideram un alt exemplu de fenomen aleatoe: Ploua, si sa consideram doua suprafete de pavaj. D

Nu putem prevedea un rezultat imediat, privind caderea unei picaturi pe aceste pavaje. Rezultatul final, insa, da. Numarul picaturilor cazute pe cele doua pavaje sunt proportionale cu suprafetele S, D.

, reprezinta probabilitatea ca o picatura cazuta pe D, sa fi cazut si pe D.

2.4 Aplicatii, exercitii, exemple:

20 de jucatori participa la un concurs. Cei 20 sunt impartiti in doua grupe a cate 10 jucatori. Care este probabilitatea ca cei mai buni 2 jucatori sa ajunga in aceeasi grupa?

Nr cazurilor posibile : 19 Pt al doilea Nr cazurilor favorabile: 9 primul exista

Cu cifrele 1,2,3,4,5,6,7,8,9 formam un nr cu 2 cifre. Care este prob. ca acest nr sa fie un numar impar?

21

1222..92

..22

1424.94

5 ..25

16.26..96

29

Cazuri posibile = 81

Cazuri favorabile = 45

C3

3. Camp conditionat de probabilitate. Evenimente independente.

3.1 Definitie:

Fie (Ω,K,P) un camp de probabilitate, si fie , (Ω = multimea evenimentelor elementare, K = multimea evenimentelor, P - probabilitatea). Alegem pentru inceput . Functia

Data prin o numim probabilitate conditionata (probabilitatea lui A conditionat de B).

Pentru egalitatea de mai sus se foloseste si notatia sau simplu (probabilitatea lui A conditionat de B). .

Formula de inmultire a probabilitatilor. Fie si presupunem atunci:

Pentru n=2 Vom presupune acum ca formula de inmultire a probabilitatilor este adevarata pentru n-1, adica are loc.

=folosim ipoteza inductiei Evenimentele A si B sunt independente daca =, adica daca .

3.3 Exemple (intersectie - independenta reuniune - compatibilitate)

a) Probabilitatea intersectiei (dependenta-independenta)

b) Probabilitatea reuniunii (compatibilitate -incompatibilitate)

Doua clase A si B au cate 30 de elevi cu respectiv cate 15 elevi buni, 10 medii, 8 slabi. Un profesor asculta la intamplare cate un elev din fiecare clasa si premiaza clasa a carei elevi se dovedeste a fi mai buna. Se cere sa se calculeze probabilitatea ca sa fie premiata clasa A.

15 buni (A₁) 10 buni (B₁)

A 10 medii (A₂) B 12 medii (B₂)

5 slabi (A₃) 8 slabi (B₃)

P(A) ∙ P(B) - daca evenimentele sunt independente (realizarea uneia nu depinde de cealalta

a)      P(A∩B)

P(A) ∙ P_A(B) - daca evenimentele sunt dependente

P(A) + P(B) - daca evenimentele sunt incompatibile (nu pot avea loc simultan

b) P(AUB)

P(A) + P(B)-P(A∩B) - daca evenimentele sunt compatibile

Exercitii:

Cuvantul "vectorial" este format din litere izolate, scrise pe cartonase. Amestecam aceste cartonase apoi extragem din ele, pe rand 4, pe care le asezam unul dupa altul in ordinea extragerii. Sa se afle probabilitatea extrageri cuvantului "voce".

Vectorial (9 litere - 9 cartonase).

V C₁ X = C₁∩ C₅∩C₃∩C₂

E C₂ P(x)=?

C C₃ P(x)=P(C₁∩ C₅∩C₃∩C₂)= P(C₁) ∙ P_C1(C₅) ∙ P_C1∩C5(C₃) ∙ P _C1∩C5∩C3(C₂) =

T C₄

O C₅

R C₆

I C₇

A C₈

L C₉

Variabile Aleatoare.

Cazul discret

Fie (Ω,K,P) un camp de probabilitate. Presupunem ca Ω este o multime finita. - evenimente elementare. O functie se numeste variabila aleatoare daca ,

unde . Daca si Ω este finita, atunci orice aplicatie , este o variabila aleatoare.

Exercitiul 1: Aruncarea cu zarul:

unde este evenimentul (elementar) aparitiei fetei i (i=1,2,3,4,5,6).

Aplicatia data prin este o variabila aleatoare daca . Variabile aleatoare (discrete), se scriu de obicei sub forma de tabele.

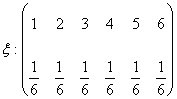→ probabilitatile corespunzatoare.

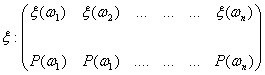
Exercitiul 2: Aruncarea cu banul: , ,

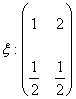
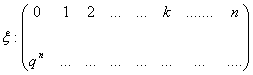
Exercitiul 3: Fie o urna ce contine bile albe si bile negre. Este cunoscuta compozitia acestei urne, deci este cunoscuta probabilitatea p de a extrage o bila alba, si probabilitatea q de a extrage o bila neagra. Facem n extrageri din urna, punand de fiecare data bila extrasa inapoi. Intelegand prin variabila aleatoare care consta in numarul de bile albe obtinute in urma acestor extrageri, sa se formeze tabelul acestei variabile aleatoare.

Tema

Curs 5

Scheme clasice de probabilitate.

a)      Schema urnei cu bile nerevenite: O urna contine bile albe si bile negre. Din aceasta urna se extrag bile fara a se pune inapoi bila extrasa (deci ). Se cere probabilitatea ca din cele n bile extrase, bile albe, iar bile negre.

b) Schema lui Boisson. Fie urnele , care contin bile albe si bile negre in proportii date (cunoastem deci numarul de bile albe si numarul de bile negre din fiecare urna, adica probabilitatea p_i , de a extrage o bila din urna U_i, si q_i probabilitatea de a extrage o bila neagra din U_i ). .

Extragand din fiecare urna cate o bila, care este probabilitatea ca sa obtinem k bile albe si n-k bile negre.

Notam cu A_i evenimentul de a extrage o bila alba din urna U_i si cu C_AI evenimentul de a extrage o bila neagra din U_i. Sa notam evenimentul

Fie 3 urne:    

U₁ U₂ U₃

p₁ p₂ p₃

q₁ q₂ q₃ Care este probabilitatea ca 2 sa fie albe si 1 neagra?

_{Coeficientul lui X}

P(x²)

Avand n urne cu bile albe si bile negre in proportii date (p_i - probabilitatea de a extrage o bila alba din U_i si q_i probabilitatea de a extrage o bila neagra), probabilitatea de a obtine k bile albe si n-k bile negre, extragand din fiecare urna cate o bila, este coeficientul lui X^k, din dezvoltarea lui ).

Binomul lui NEWTON

c) Schema urnei cu bile revenite. (Schema lui Bernoulli). O urna contine bile albe si bile negre. Fie p probabilitatea de a extrage o bila alba si q probabilitatea de a extrage o bila neagra. Se fac n extrageri succesive introducandu-se de fiecare data inapoi bila extrasa. Care este probabilitatea de a extrage k bile albe. Problema este echivalenta cu : avem n urne avand fiecare acelasi numar de bile albe si negre. (p - probabilitatea de a extrage o bila alba si q - probabilitatea de a extrage o bila neagra). Extragand din fiecare urna cate o bila, care este probabilitatea de a obtine bile albe?

coeficientul X^k:

Aruncam cu un zar de 9 ori. Care este probabilitatea ca de 5 ori sa obtinem un numar mai mare decat 4?

n = 9;    k = 5;

=