| CATEGORII DOCUMENTE |
| Demografie | Ecologie mediu | Geologie | Hidrologie | Meteorologie |
Sisteme de coordonate si proiectii cartografice
Un punct in spatiu poate fi localizat prin 3 sisteme de coordonate: coordonate carteziene, coordonate geografice si coordonate in proiectie.
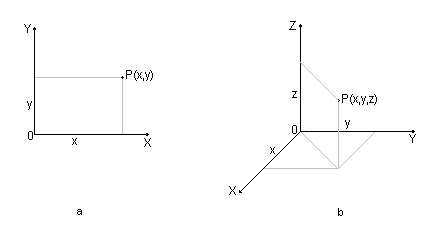 Figura 1 Sisteme
de coordonate carteziene in doua si trei dimensiuni
Figura 1 Sisteme
de coordonate carteziene in doua si trei dimensiuni
1. Coordonatele carteziene in plan sunt definite de proiectiile razei vectoare pe cele doua axe, iar in spatiu de proiectiile razei vectoare pe cele trei axe. In figura 1 am reprezentat cele doua tipuri de coordonate in sisteme rectangulare (cu axe perpendiculare). Cele bidimensionale comporta o origine arbitrara fata de care se face referire si de regula are pozitia fixata in partea stanga jos astfel incat sa avem doar valori pozitive pentru Ox si Oy. In cazul tridimensional originea se ia in centrul Pamantului, axa Oz fiind confundata cu axa de rotatie. Coordonatele unui punct se exprima prin proiectiile sale pe cele trei axe, fiind un triplet (x,y,z). Uneori este mai comod sa se lucreze in coordonate polare in plan sau coordonate sferice in spatiu. In cazul in care avem tripletul (r,φ,θ), adica distanta la origine si unghiurile formate de raza vectoare cu axa Ox, respectiv cu Oz.
In cazul coordonatelor polare avem perechea (r,θ) care este legata de cele carteziene prin formulele:
x r cos
y = r sin unde r = (x2+y2)1/2, 0≤ p
Formulele de trensformare din coordonate cartziene in coordonate sferice sunt:
x r sin cos
y = r sin sin
z = r cos unde r = (x2+y2+z2)1/2, 0≤ p p
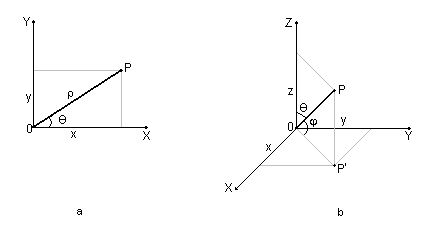 Figura 2 Sistemele de coordonate polare si sferice
Figura 2 Sistemele de coordonate polare si sferice
Coordonatele geografice se exprima intr-un sistem de referinta cu originea in centrul Pamantului, axa fundamentala fiind axa de rotatie, iar plan fundamental planul ecuatorului terestru. Sistemul de coordonate geografice este asemanator cu sistemul de coordonate sferice, cu originea tot centrul Pamantului, meridianul Greenwich este continut in planul xOz si ecuatorul este continut in planul xOy. In cazul coordonatelor geografice altitudinea nu este exprimata prin lungimea razei vectoare (adica distanta de la centrul Pamantului la punct) deoarece originea este greu de precizat, ci este exprimata fata de o suprafata de referinta numita nivelul marii, care implica faptul ca Pamantul este considerat un geoid. Suprafata de referinta nu este cunoscuta exact decat la nivelul marilor si oceanelor. Sub continente, geoidul este o forma teoretica care trebuie reconstituita prin masuratori.
Figura 3 Coordonate
geografice

Coordonatele geografice sunt:
- latitudinea ( ) unui loc este unghiul format de planul ecuatorului terestru cu verticala locului;
- longitudinea ( ) este unghiul format de meridianul initial (Greenwich) cu meridianul locului (figura 3).
Pentru pozitionarea in spatiu a unui punct se mai introduce cota, sau inaltimea punctului deasupra nivelului marii. Distanta de la punct la centrul Pamantului (geoid), este mult mai dificil de evaluat.
3. Coordonate elipsoidale. Termenul de coordonate elipsoidale este folosit pentru coordonatele geografice la care altitudinea este exprimata in raport cu suprafata unui elipsoid de rotatie. Satelitii furnizeaza, in general, coordonatele elipsoidale (GPS).
Coordonate in proiectie. Trecerea de la coordonate carteziene sau geografice la coordonate in proiectie presupune aducerea tuturor punctelor de pe suprafata Pamantului pe un elipsoid de referinta, eliminandu-se astfel neregularitatile geoidului. Transformarea coordonatelor se face prin formule matematice stabilite pentru fiecare grup de proiectii.
Din punct de vedere matematic, suprafata Pamantului poate fi considerata o sfera, un elipsoid de revolutie sau un elipsoid triaxial. Desi nici una din corpurile mentionate nu reprezinta forma exacta a Pamantului, din considerente practice Pamantul va fi considerat, in functie de precizia reprezentarii, ca fiind unul din cele trei corpuri. Programele incorporate in GIS sunt concepute de asa maniera incat sa rezolve cat mai multe situatii. In documentatii se gasesc toate detaliile privitoare la aceasta problema. De exemplu Arc/Info, in cazul sferic considera raza medie a Pamantului de 6.370.997 m. In cazul in care Pamantul este considerat elipsoid de revolutie, elipticitatea se apreciaza la o valoare medie de 0.003353. In aceasta situatie diferenta intre o harta obtinuta de pe un Pamant considerat sferic si pe un Pamant considerat eliptic, nu este prea mare. Se apreciaza ca hartile la scara 1:5.000.000 nu pot sesiza diferenta. In cazul hartilor cu scari de 1:1.000.000 sau mai mari, pentru a mentine acuratetea, este nevoie ca Pamantul sa fie considerat un elipsoid. Mentionam ca uneori in locul notiunii de elipsoid se foloseste si termenul de sferoid, adica un corp aproape sferic. Produsele GIS percep o larga varietate de elipsoizi.
In termeni matematici proiectia cartografica poate fi definita ca o corespondenta unu la unu dintre punctele de pe suprafata sferei sau a elipsoidului si punctele proiectate pe un plan. Expresiile generale de transformare directe si inverse sunt:
x=f2(u,v), y=f2(u,v), (1)
u=F1(x,y), v=F2(x,y), (2)
Unde u si v pot fi coordonate geografice (f l), geodezice, sau alt tip de coordonate curbilinii, iar x si y sunt coordonatele carteziene. Functiile f1, f2, F1, F2 sunt continue pana la ordinul II al derivatelor partiale corespunzatoare variabilelor fiecarei functii.
Procesul de transformare a datelor de pe o sfera sau elipsoid pe o suprafata plana, distorsioneaza cel putin una din caracterisici: forma, unghiurile, suprafata, distanta si directia. Deoarece masuratorile pe harta conduc la luarea deciziilor este necesar sa se stie de la inceput ce proiectie distorsioneaza o anumita caracteristica si ce nu. De cele mai multe ori ele conserva o singura caracteristica. Dupa marimile care sunt conservate se disting patru tipuri de proiectii.
Proiectia conforma conserva unghiurile. Cu alte cuvinte un unghi masurat pe suprafata Pamantului va avea aceeasi masura cu un unghi evaluat pe harta in proiectie. Aceasta conduce si la conservarea locala a formelor, adica a suprafetelor relativ mici. Pentru suprafete mari forma nu se conserva. De fapt nici o proiectie nu poate pastra suprafete de mari dimensiuni. Proiectia stereografica este un caz particular de proiectie conforma in care scara creste dinspre centru inspre periferie.
2) Proiectia echivalenta conserva suprafetele dar nu si forma, astfel ca, un patrat poate fi reprezentat printr-un dreptunghi, dar de aceeasi arie. Pentru regiuni mici aceasta distorsiune este putin sesizabila. In astfel de proiectii meridianele si paralelele nu se intersecteaza in unghiuri drepte.
Proiectia echidistanta conserva distantele dintre puncte. Scara nu se mentine constanta pe intreaga harta la nici o proiectie. Au ca suprafata de proiectare suprafete desfasurabile (cilindru, con).
Proiectia azimutala conserva directia. Distanta dintre doua puncte de pe suprafata Pamantului considerat sferic se masoara pe un cerc mare, iar pe un Pamant elipsoid se masoara pe un arc de elipsa.
Dupa suprafata pe care se proiecteaza distingem: (a) proiectia pe un plan, (b) proiectia pe o suprafata conica si (c) proiectia pe o suprafata cilindrica. Ultimele doua sunt suprafete desfasurabile, astfel ca, in final vom avea tot o proiectie bidimensionala. In cele ce urmeaza vom prezenta pe scurt cele trei categorii de proiectii.
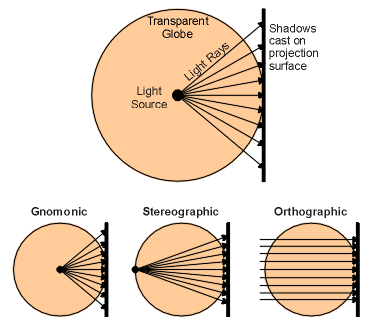
(a) Proiectia se realizeaza de obicei pe un plan tangent la sfera intr-un punct, dar poate fi si secant (figura 4). Este o proiectie azimutala, deci care conserva directia. Punctul de tangenta poate fi Polul nord, sud, un punct de pe Ecuator sau orice alt punct intermediar rezultand trei aspecte: polar, ecuatorial si oblic. Cel mai simplu si altminteri cel mai uzitat este aspectul polar. In aceasta situatie paralelele devin prin proiectie cercuri concentrice, iar meridianele sunt drepte convergente spre pol (punctul de tangenta). Proiectiile azimutale se deosebesc prin punctele din care se realizeaza perspectiva. Astfel deosebim proiectia gnomomica, in care punctul de perspectiva este centrul Pamantului, stereografica in care punctul de perspectiva este polul opus si ortografica cand punctul de perspectiva se afla la infinit (figura 5).
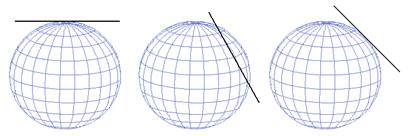 Figura 4 Proiectii pe un plan
secant si tangent la sfera
Figura 4 Proiectii pe un plan
secant si tangent la sfera
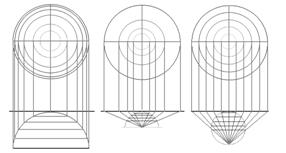
(b) Proiectia conica cea mai simpla se obtine cand suprafata conica este tangenta la sfera (figura 6). Paralela la care conul este tangent se numeste paralela de referinta sau standard. Este exclusa situatia cand paralela standard este Ecuatorul; aceasta situatie genereaza proiectia cilindrica (vezi mai jos). Meridianele sunt convergente spre pol. Pe paralela standard nu exista deformari. Acestea apar inspre N si S. Polul nu este corect reprezentat, astfel ca, se procedeaza la selectionarea conului in vecinatatea lui. O alta varianta a proiectiei conice este atunci cand suprafata conica este secanta la suprafata Pamantului (figura 7).
Figura 5 Proiectia ortografica,
gnomomica si stereografica
Aceasta situatie defineste doua paralele standard. Distorsiunea nu este aceeasi pentru regiunile dintre paralele standard si inspre N si S. Proiectia Lambert este un exemplu de proiectie conica conforma (tangenta).
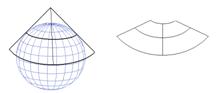 Figura 6 Proiectie
conica tangenta
Figura 6 Proiectie
conica tangenta
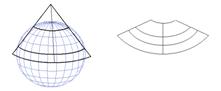 Figura 7 Proiectie
conica secanta
Figura 7 Proiectie
conica secanta
(c) Proiectia cilindrica este o proiectie pe o suprafata cilindrica desfasurata. Sfera sau elipsoidul poate fi tangenta (figura 8) sau secanta (figura 9) la cilindru. Proiectia Mercator este una din cele mai uzuale proiectii cilindrice, ecuatorul fiind linia de tangenta. Pe suprafata proiectata si desfasurata, meridianele sunt echidistante iar distanta intre paralele creste inspre pol. Este o proiectie conforma. Exista trei feluri de proiectii cilindrice: normala (cea prezentata mai sus), transversala si oblica. Proiectia transversala cea mai cunoscuta este UTM (Universal Transverse Mercator) in care cercul de contact este primul meridian, sau linii paralele cu meridianul in cazul secant. Este o proiectie conforma. Scara este constanta numai de-a lungul meridianului central. Are avantajul ca acopera toate latitudinile. In cazul oblic cercul de contact este un cerc mare arbitrar. In toate proiectiile cilindrice liniile de tangenta, sau cele secante, nu au distorsiuni si astfel liniile sunt echidistante.
In Romania se foloseste proiectia stereografica pe elipsoidul Krasowski (1940). Proiectia Gaus-Kruger, care este o proiectie cilindrica transversala, se foloseste pentru harti la scara mare 1:25.000, 1:50.000, 1:100.000.
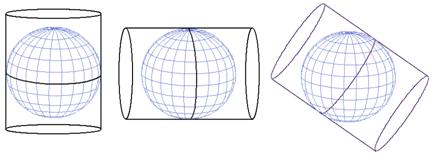 Figura 8 Proiectia cilindrica tangenta
Figura 8 Proiectia cilindrica tangenta
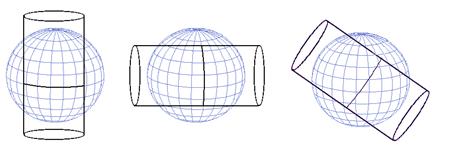 Figura 9 Proiectia cilindrica secanta
Figura 9 Proiectia cilindrica secanta
Proprietati ale unor proiectii cartografice
|
Proiectie |
Tip |
conserva unghiurile |
conserva suprafetele |
conserva distantele |
conserva directia |
|
glob |
sfera |
da |
da |
da |
da |
|
Mercator |
cilindric |
da |
partial |
||
|
Transverse Mercator |
cilindric |
da | |||
|
oblica Mercator |
cilindric |
da | |||
|
ortografica |
azimutal |
partial |
|||
|
stereografica |
azimutal |
da |
partial |
||
|
gnomica |
azimutal |
partial |
|||
|
azimutala echidistanta |
azimutal |
partial |
partial |
||
|
azimutala Lambert |
azimutal |
da |
partial |
||
|
conforma conica Lambert |
conic |
da |
partial |
||
|
echidistant conica |
conic |
partial | |||
|
policonica |
conic |
partial | |||
|
biplolara oblica conic conforma |
conic |
da |
|
Tipuri de harti in functie de proiectia cartografica
|
Proiectie |
Tip |
Harti topografice |
Harti geologice |
Harti tematice |
Prezentari |
Navigatie |
|
glob |
sfera |
da |
da | |||
|
Mercator |
cilindric |
da |
da |
da |
||
|
Transverse Mercator |
cilindric |
da |
da | |||
|
oblica Mercator |
cilindric |
da | ||||
|
orthografica |
azimutal | |||||
|
stereografica |
azimutal |
da |
da |
da |
||
|
gnomonica |
azimutal |
da |
da |
|||
|
azimutala echidistanta |
azimutal |
da | ||||
|
azimutala Lambert |
azimutal |
da |
da | |||
|
conforma conica Lambert |
conic |
da |
da |
da |
da |
|
|
echidistant conica |
conic | |||||
|
policonica |
conic |
da | ||||
|
biplolara oblica conic conforma |
conic |
da |
Scara de reprezentare in functie de proiectia cartografica
|
Proiectie |
Tip |
Terra |
Emisfere |
Continente/ |
Regiuni/ |
Scara medie |
Scara mare |
|
glob |
sfera |
da |
| ||||
|
Mercator |
cilindric |
partial |
da | ||||
|
Transverse Mercator |
cilindric |
da |
da |
da |
da |
||
|
oblica Mercator |
cilindric |
da |
da |
da |
da |
||
|
ortografica |
azimutal |
partial | |||||
|
stereografica |
azimutal |
da |
da |
da |
da |
da |
|
|
gnomica |
azimutal |
partial | |||||
|
azimutala echidistanta |
azimutal |
partial |
da |
da |
da |
partial |
|
|
azimutala Lambert |
azimutal |
da |
da |
da | |||
|
conforma conica Lambert |
conic |
da |
da |
da |
da |
||
|
echidistant conica |
conic |
da |
da | ||||
|
policonica |
conic |
partial |
partial |
||||
|
biplolara oblica conic conforma |
conic |
da |
Deformarile, in functie de tipul de proiectie
a) proiectii azimutale
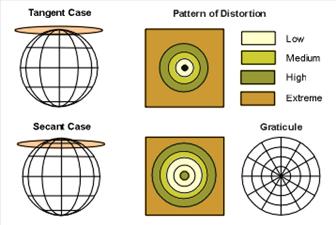
b) proiectii cilindrice
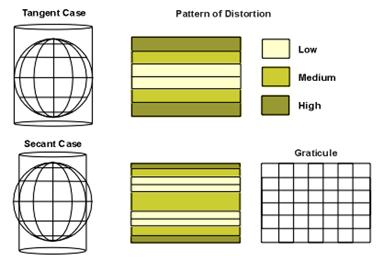
c) proiectii conice
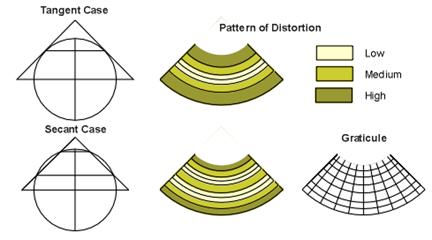
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 7531
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved