Parametrii variatiei

Parametrii variatiei

Studiul unor populatii statistice prezinta importanta numai din punct de vedere al unor marimi care variaza de la o unitatea la alta sau de la un grup de unitati la altul.

Valorile inregistrate de o variabila cantitativa, in raport cu care este studiata o populatie, se datoresc actiunii diferitilor factori esentiali si neesentiali.

Intensitatea diferita cu care se pot manifesta factorii esentiali cat si sensul contrar cu care pot actiona factorii neesentiali in raport cu fiecare unitate, provoaca nivele diferite inregistrate de variabile in raport cu care este studiata populatia.

Problema masurarii variatiei unei variabile cantitative este importanta pentru a vedea in ce masura valoarea medie a acesteia poate reprezenta intrega populatie.

Daca abaterile de la valoarea medie sunt neesentiale atunci se poate afirma ca populatia este omogena si ca acest parametru poate reprezenta tendinta centrala, iar daca aceste abateri sunt mari atunci populatia este eterogena si valoarea medie nu are capacitatea de a reprezenta populatia.

Pentru unele serii, valoarea medie nu se poate calcula. In asemenea cazuri, parametrul valoarea mediana poate sa-i ia locul. Aceeasi problema se pune si in acest caz, de a vedea in ce masura valoarea mediana este sau nu reprezentativa pentru populatia in cauza.

O alta problema care nu se poate rezolva fara a studia si masura variatia inregistrata de o variabila in raport cu care este studiata o populatie, o constituie verificarea de ipoteze. In activitatea practica, de multe ori pornind de la valorile unor parametrii calculati pe baza datelor culese relativ la un numar mic de unitati, este necesar a fi extinsi la nivelul intregii populatii sau de a se verifica anumite ipoteze statistice.

Parametrii variatiei se pot calcula atat sub forma absoluta cat si relativa, si masoara imprastierea valorilor unei variabile cantitative fata de valoarea medie sau valoarea mediana.

Ca urmare, in functie de elementul de referinta folosit in masurarea variatiei, deosebim:

parametrii variatiei in raport cu valoarea medie;

parametrii variatiei in raport cu valoarea mediana.

1. Parametrii variatiei in raport cu valoarea medie

Abaterea medie liniara

Abaterea medie liniara, notata cu , reprezinta media aritmetica a abaterilor variabilei X de la valoarea medie a acesteia, luate in valoare absoluta:

(2.33)

Relatia (2.33) se particularizeaza in :

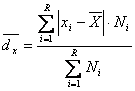(2.34)

Daca seria are la baza o variabila continua si se cunoaste f(x), atunci abaterea medie liniara se calculeaza astfel:

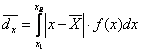(2.35)

Densitatea de probabilitate f(x) se poate aproxima cu densitatea empirica si atunci pentru abaterea medie liniara se pot obtine relatii de calcul aproximativ, frecvent utilizate in activitatea practica, de forma:

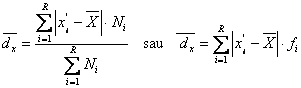(2.36)

dupa cum seria in cauza este formata cu frecvente absolute sau relative, unde:

este mijlocul intervalului "i".

Acest parametru serveste caracterizarii sintetice a gradului de reprezentativitate a valorii medii, aratand cu cat    se abate in medie orice valoare a variabilei X de la valoarea medie , intr-un sens sau altul.

Sub forma relativa, acest indicator poarta denumirea de coeficient simplu de variatie si se calculeaza conform relatiei:

(2.37)

Coeficientul simplu de variatie (V_x) arata cu cat se abate in medie orice valoare a variabilei X de la valoarea medie echivalenta cu 1 sau 100%. Calculat pentru doua serii diferite, se poate aprecia gradul de reprezentativitate a celor doua medii. Se apreciaza mai reprezentativa acea valoare medie pentru care coeficientul simplu de variatie este mai mic.

Parametrul abaterea medie liniara, in forma absoluta sau relativa, prezinta unele deficiente deoarece nu este suficient de sensibil la abaterile mici, adaugandu-se si unele inconveniente de natura teoretica, generate de exprimarea abaterilor in valoarea absoluta.

Inlaturarea acestor deficiente se poate realiza apeland la un nou parametru privind masurarea variatiei, numit abatarea medie patratica.

Abaterea medie patratica

Acest indicator este utilizat atat pentru caracterizarea gradului de reprezentativitate a valorii medii cat si in scopul estimarii unor parametri necunoscuti.

Abaterea medie patratica, notata cu σ_x , se defineste ca fiind media patratica a abaterilor valorilor variabilei X, de la valoarea medie , adica:

(2.38)

Un calcul intermediar in aflarea acestui parametru, il constituie calcularea patratului abaterii medii patratice, care se numeste dispersie sau varianta si are urmatoarea expresie de calcul:

(2.39)

V(x) reprezinta o alta notatie pentru varianta, pe langa σ²_x .

Varianta fiind un calcul intermediar in aflarea abaterii medii patratice, in cele ce urmeaza se va prezenta modul de calcul al acesteia.

Relatia de calcul a variantei se particularizeaza in raport cu tipul seriei. In cazul unei serii care are la baza o variabila X discreta, conform definitiei, varianta are expresia:

(2.40)

In cazul unei serii care are la baza o variabila X continua, varianta se calculeaza conform urmatoarei relatii:

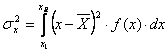(2.41)

a carei aplicare presupune cunoasterea densitatii de repartitie f(x).

Pentru o serie data, varianta calculata nu are interpretare, dar daca se extrage radacina patrata din acesta se obtine un numar care se exprima in aceleasi unitati de masura ca si variabila de la baza seriei. Acest numar (valoare) reprezinta abaterea medie patratica, simbolizand cu cat se abate in medie in plus sau minus orice valoare x_i a variabilei X de la valoarea medie .

Parametrul abaterea medie patratica se poate exprima si sub forma relativa, caz in care se numeste coeficientul de variatie a lui Pearson, si se noteaza cu V_x. Expresia de calcul este:

(2.42)

si reprezinta abaterea medie a orcarei valori a variabilei X de la valoarea medie, considerata egala cu 1 sau 100.

Coeficientul de variatie a lui Pearson calculat pentru doua sau mai multe serii, poate fi folosit in aprecieri comparative privind gradul de reprezentativitate a valorii medii calculate.

Deoarece gradul de reprezentativitate a valorii medii este in raport invers cu marimea coeficientului de variatie a lui Pearson, se poate afirma, in cazul mai multor serii, ca este mai reprezentativa valoarea medie a acelei serii pentru care V_x este mai mic.

In concluzie, trebuie retinut ca parametrul abaterea medie patratica sub forma absoluta σ_x si sub forma relativa V_x sunt indicatori fundamentali utilizati in masurarea variatiei unei variabile.

Atat abaterea medie liniara, cat si abaterea medie patratica constituie o masura a variatiei medii, primul o medie de ordinul unu, iar al doilea o medie de ordinul doi .

2. Parametrii variatiei in raport cu valoarea mediana

Abaterea interquartila

Abaterea interquartila, prin definitie, este media aritmetica simpla a segmentelor M_e - Q₁ si Q₃ - M_e, respectiv:

(2.43)

si arata cu cat se abat in medie, in plus sau in minus, de la mediana, cele 50% din valorile variabilei cuprinse intre Q₁ si Q₃.

Forma relativa a acestui indicator notat cu Q_r:

(2.44)

se numeste coeficient de variatie interquartilic si arata cu cat se abat in medie de la mediana (considerata egala cu 100), valorile variabilei inregistrate pentru cele 50% din unitatile populatiei cuprinse intre Q₁ si Q₃.

Ca atare, se apreciaza ca imprastierea unitatilor in cadrul populatiei studiate este cu atat mai mare, in raport cu variabila de studiat, cu cat abaterea interquartila in valoarea absoluta (2.43) sau relativa (2.44) este mai mare.

Abaterea interquantila

Pentru acest parametru, sub forma absoluta, avem:

(2.45)

iar sub forma relativa denumita si coeficient de variatie interquantilic este:

(2.46)

Cu cat abaterea interquantilica (relativa sau absoluta) este mai mica, cu atat valoarea mediana este mai reprezentativa.