Ecuatia constitutiva a fluidelor ideale si reale

Ecuatia constitutiva a fluidelor ideale si reale

Actiunea fortelor aplicate unui mediu continuu deformabil este caracterizata prin tensorul eforturilor unitare . Raspunsul mediului la aceasta stare de eforturi consta in variatia in interiorul sau a unor marimi cinematice, termodinamice s.a.m.d.

Starea de variatie a marimilor cinematice este caracterizata inclusiv prin matricea vitezelor de deformare .

Legatura dintre cauza si efect (deformatii), se numeste ecuatia constitutiva a mediului continuu considerat.

(ecuatia lui Hooke)

(experienta lui Newton )

Vom analiza doua cazuri intalnite in practica:

Fluidul ideal (fluidul lipsit de vascozitate )

Fluidul real in miscare laminara ()

Fluidul ideal

, si deci:

sau

Daca notam , atunci ceea ce subliniaza ca efortul unitar normal este intotdeauna o compresiune,scalarul numindu-se presiunea din punctul curent considerat.

Observatie: Din punct de vedere al acestei stari de eforturi, cazul fluidului ideal seamana foarte mult cu repausul fluidului.

Se poate introduce tensorul a carui matrice asociata este:

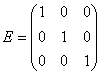si cu , avem:

(ecuatia constitutiva a fluidelor ideale)

Fluidul real

Consideram un fluid real, , omogen si izotrop aflat in miscare laminara, cea mai simpla ipoteza privind relatia constitutiva se scrie astfel:

, unde a si b sunt scalari

este o functie liniara de tensorul vitezelor de deformare .

Aceasta ecuatie sugereaza o variatie liniara intre parametrii considerati:

a)      Un parametru unghiular care nu depinde de variabilele ecuatiei si , si care in realitate reprezinta o proprietate fizica a fluidului: (valabil in cazul fluidelor Newtoniene);

b)      Este o functie liniara de variabilele si si un invariant fata de schimbarea axelor de coordonate (caci fluidul este izotrop) ceea ce va conduce la:

dar conform ecuatiei de continuitate in cazul fluidelor incompresibile,

(ecuatia constitutiva pentru cazul fluidului real)

In cazul fluidului compresibil sunt doua elemente constitutive, vascozitatea si presiunea.