Modelarea cinematica a transmisiei bicardanice excentrice de tip 3RT3R

Modelarea cinematica a transmisiei bicardanice excentrice de tip 3RT3R

1. Introducere

In transmisiile bicardanice destinate laminoarelor, o directie moderna de optimizare se refera la folosirea excentricitatii, ca posibilitate de montare a unor rulmenti cu capacitati portante superioare. Aceasta idde a fost aplicata de firma germana Voith pentru transmisii bicardanice destinate antrenarii laminoarelor grele; astfel firma Voith produce curent transmisii bicardanice in varianta sinfazata (heterocinetica). Desi frapant, firma Voith a utilizat aceasta varianta din doua motive:

a) unghiul (unghiul dintre axele arborilor de intrare si iesire) si turatia de de functionare este foarte redusa (cateva rot/min); implicit efectul heterocinetismului devine superflu;

b) deplasarea relativa din cupla intermediara de translatie devine foarte redusa pentru varianta sinfazata, fapt care asigura capacitatea portanta maxima a acestei cuple (suprafata de contact dintre caneluri ramane practic nemodificata in timpul functionarii).

Din pacate in literatura exista putine date referitoare la acest tip transmisie . Ca urmare, in acest capitol se efectueaza, mai intai modelarea cinematica completa, pentru varianta Voith. Pentru comparatie, se efectueaza apoi modelarea cinematica a transmisiei bicardanice excentrice ortofazata (homocinetica). In final se prezinta concluzii utile privind comparatia celor doua transmisii.

2. Modelarea cinematica a transmisiei bicardanice excentrice de tip 3RT3R sinfazata

Ca urmare, se prezinta modelul cinematic al transmisiei bicardanice excentrice de tip 3RT3R, in varianta sinfazata (in pozitie initiala, furcile 1 si 4 se afla in acelasi plan; vezi fig.1).

Modelarea cinematica pleaca de la schema si notatiile din fig.1; notatiile utilizate au urmatoarea semnificatie: e = AB = CD reprezinta excentricitatea crucilor cardanice (distanta dintre axele bratelor unei cruci cardanice); l₁ = BC reprezinta lungimea arborelui intermediar (distanta dintre axele cuplelor de rotatie ale furcilor intermediare).

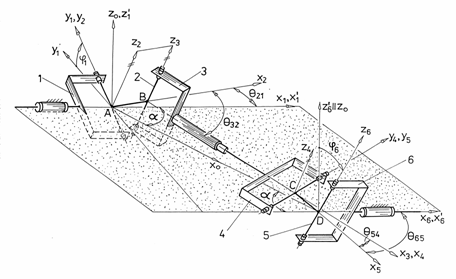
Fig. 1. Schema si notatii utilizate in modelarea cinematica a mecanismul bicardanic excentric sinfazat (heterocinetic) 3RT3R

Metoda clasica, de modelare cinematica, bazata pe folosirea operatorilor omogeni, conduce la relatia matriceala:

(1)

in care prin s-a notat matricea de trecere din triedrul x_ny_nz_n in triedrul x_my_mz_m.

Pentru eludarea dificultatiilor ridicate de aceasta metoda, in continuare se aplica o metoda mixta: se combina metoda operatorilor omogeni cu metoda legaturilor geometrice. Astfel, se scriu transformarile matriceale:

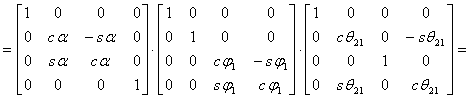
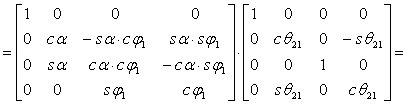
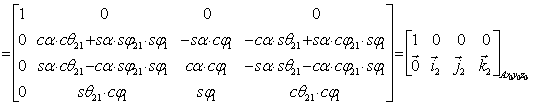(2)

Se exprima matricea , care face trecerea de la triedrul Cx₅y₅z₅ la triedrul Ax₀y₀z₀, cu ajutorul transformarilor (vezi fig.1):

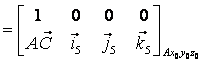(3)

in care prin s si c sunt notate prescurtarile functiilor sinus si respectiv cosinus.

Conform fig. 1 si relatiilor (2) si (3) se poate scrie:

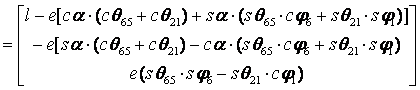(4)

Din analiza fig. 1 se desprind urmatoarele conditii de legatura, care permit determinarea marimilor geometrice caracteristice mecanismului:

(5)

(6)

(7)

Pe baza relatiilor (2) si (3), conditiile (5), (6) si (7) devin:

(5')

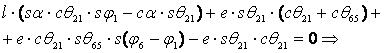
(6')

Inmultind relatia (6') cu si tinand seama de relatia (5'), rezulta:

; (6")

(6''')

(7')

Inmultind relatia (7') cu si tinand seama de relatia (5'), se obtine:

; (7")

(7''')

Inlocuind in (7''') , rezulta:

(8)

Inmultind relatia (8) cu si tinand seama de relatia (5'), se obtine:

(8')

Pe de alta parte, din relatia (6''') rezulta:

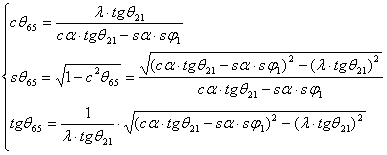(9, 10, 11)

iar din relatia (11), tinand seama de relatia (5'), se obtine:

(12)

Functiile si se obtin prin rezolvarea numerica pe calculator a sistemului format din ecuatiile (8') si (12):

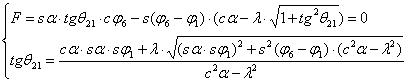(13)

Solutiile sistemului (13) permit determinarea unghiului cu ajutorul relatiei (7'''):

(14)

Cunoscand marimile si (in functie de ), se poate determina lungimea momentana a arborelui intermediar BC:

(15)

Considerand unghiulindependent si marimile cunoscute, pe baza relatiilor de mai sus se propune urmatorul algoritm de calcul: se determina abaterea de la homocinetism prin rezolvarea sistemului (13); valoarea acesteia se introduce in expresiile marimilor si ; pe baza acestora se poate determina variatia lungimii arborelui intermediar BC.

Pentru valoriile ; l=1800 mm, e=150 mm si in urma simularilor pe calculator s-au obtinut diagramele din fig. 2, explicitarea diagramelor sunt realizate prin titlurile asociate fiecareia dintre acestea:

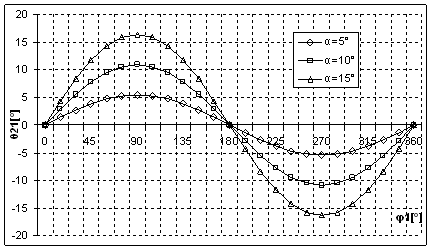
Fig. 2. a Variatia unghiului in functie de la valori ale unghiului

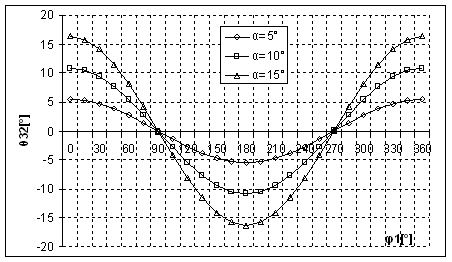
Fig. 2. b Variatia unghiului in functie de la valori ale unghiului

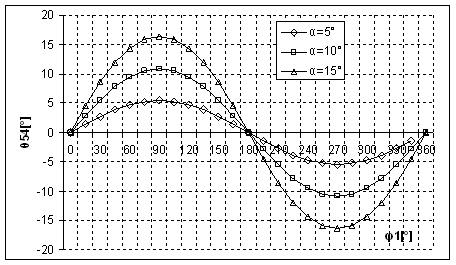
Fig. 2. c Variatia unghiului in functie de la valori ale unghiului

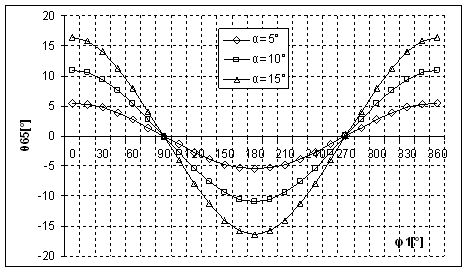
Fig. 2. d Variatia unghiului in functie de la valori ale unghiului

Fig. 2. e Variatia lungimii arborelui intermediar BC in functie de la valori ale unghiului

Fig. 2. f Abaterea de la homocinetism in functie de la valori ale unghiului

Modelarea cinematica a transmisiei bicardanice excentrice de tip 3RT3R ortofazata

Comparativ, este realizata si modelarea cinematica a mecanismului bicardanic excentric 3RT3R in varianta ortofazata; schema si notatiile utilizate sunt prezentate in fig. Algoritmul folosit este asemanator cu cel din prima parte a capitolului, cu precizarea ca inserierea este ortofazata, ceea ce implica urmatoarele modificari (vezi fig.3):

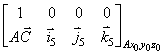
    (16)

, , (17), (18), (19)

Fig. Mecanismul bicardanic excentric 3RT3R in varianta ortofazata (homocinetica)

In urma prelucrarilor matematice se obtin urmatoarele dependente, care modeleaza geometria cinematica a mecanismului homocinetic:

    (17')

    (18')

(19')

Prin explicitarea relatiilor precedente, se obtine lungimea arborelui intermediar si variatia acestuia:

;

(20)

In fig. 4.f se prezinta comparativ variatiile maxime ale lungimii arborelui intermediar, in functie de unghiul a, dintre axele furcilor, pentru cele doua variante ale mecanismului bicardanic excentric: ortofazata (homocinetica) si sinfazata (heterocinetica).

Fig. 4. a Variatia unghiului in functie de la valori ale unghiului

Fig. 4. b Variatia unghiului in functie de la valori ale unghiului

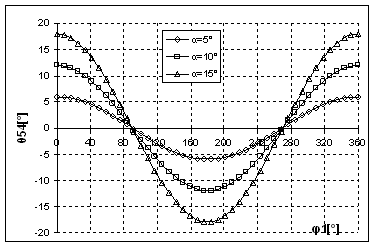
Fig. 4. c Variatia unghiului in functie de la valori ale unghiului

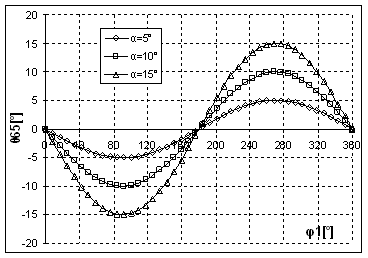
Fig. 4. d Variatia unghiului in functie de la valori ale unghiului

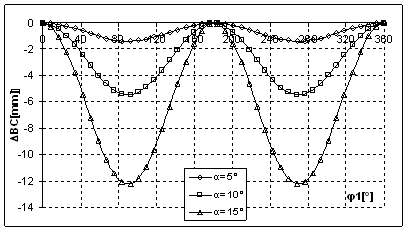
Fig. 4. e Variatia lungimii arborelui intermediar BC in functie de la valori ale unghiului

Fig. 4. f Variatia lungimii arborelui intermediar BC in functie de unghiul

4. Concluzii

In urma analizei comparative a rezultatelor obtinute in urma analizei cinematice a celor doua transmisii bicardanice excentrice (varianta sinfazata si varianta ortofazata) se desprind urmatoarele concluzii:

• Rezultatele teoretice obtinute pentru transmisia sinfazata concorda cu datele oferite de firma Voith
• Spre deosebire de varianta ortofazata (vezi fig.) care este homocinetica (), varianta sinfazata (vezi fig.1.) este heterocinetica; abaterea de la homocinetism () variaza periodic (vezi fig. 2.f) cu perioada 180 , amplitudinea acesteia crescand rapid cu cresterea unghiului ;
• Deplasarile unghiulare (vezi figurile 2. si 4.) au variatie sinusoidala in ambele cazuri dar sunt defazate cu 90 grade;
• Comparativ cu mecanismul bicardanic sinfazat (heterocinetic), la mecanismul ortofazat (homocinetic) variatia lungimii arborelui intermediar este foarte mare (vezi fig. 4,f);
• Variatia foarte redusa a deplasarii arborelui intermediar la varianta sinfazata are ca avantaj mentinerea unei suprafete de contact aproximativ constanta, dar nu se elimina forta axiala de frecare din cupla de translatie;
• In conditiile laminoarelor grele (), devine deci favorabila utilizarea mecanismelor bicardanice excentrice sinfazate, care asigura, pe de o parte, o variatie foarte redusa o lungimii arborelui intermediar si, pe de alta parte, permite montarea unor rulmenti de dimensiuni mari prin utilizarea de cruci cardanice excentrice;
• Diminuarea / eliminarea fortei axiale de frecare poate fi realizata prin inlocuirea cuplei axiale de traslatie printr-o cupla excentrica de rotatie rezultand o structura de tip 7R, care constituie obiectul capitolului urmator (cap. 4).