| CATEGORII DOCUMENTE |
| Aeronautica | Comunicatii | Electronica electricitate | Merceologie | Tehnica mecanica |
TENSORII TENSIUNII SI deformaTiilor infinitezimale
Deoarece pentru a se stabili conditiile de aparitie a diferitelor ruperi în structuri este necesara cunoasterea câmpurilor de tensiuni si deformatii în diferite zone ale structurii, pentru început, în acest capitol, se va face o prezentare succinta a principalelor elemente ce permit estimarea valorilor acestor câmpuri.
1 Tensori de ordinul doi
Fie V un spatiu vectorial.
Atunci o functie liniara T definita pe V cu valori în V se numeste tensor de ordinul al doilea
![]() T:V V (1)
T:V V (1)
![]() = T (
= T (![]() ) = T
) = T ![]() (2)
(2)
Proprietatea de liniaritate a
tensorului ![]() se exprima prin
relatia:
se exprima prin
relatia:
T a ![]() + b
+ b ![]() ) = a T
) = a T ![]() + b T
+ b T ![]() (3)
(3)
pentru ![]()
![]() ,
, ![]() V si a b
V si a b ![]()
Multimea tensorilor de ordinul doi se noteaza cu L.
D. Se numeste produs tensorial sau diadic a doi vectori
![]() si
si ![]() din V si se
noteaza cu
din V si se
noteaza cu ![]()
![]() L sau
L sau ![]()
![]()
![]() L, tensorul de ordinul al doilea definit prin
relatia:
L, tensorul de ordinul al doilea definit prin
relatia:
(![]()
![]() )
) ![]() =
= ![]() (
(![]()
![]()
![]() ) ,
) , ![]()
![]() V, (4)
V, (4)
unde (![]()
![]()
![]() ) reprezinta produsul scalar al vectorilor
) reprezinta produsul scalar al vectorilor ![]() si
si ![]()
D. Un sistem de p
vectori ![]() ,
, ![]() …
… ![]() p V se
numeste liniar independent daca relatia:
p V se
numeste liniar independent daca relatia:
a1 ![]() + a2
+ a2 ![]() + … ap
+ … ap ![]() = ō, (5)
= ō, (5)
unde
a1 a2 ap ![]() , nu poate avea loc decât daca a1 a2 ap =0 În caz contrar sistemul de p vectori se numeste liniar dependent
, nu poate avea loc decât daca a1 a2 ap =0 În caz contrar sistemul de p vectori se numeste liniar dependent
D. Într-un spatiu vectorial n - dimensional orice sistem liniar independent de n vectori se numeste baza.
D. O baza a spatiului vectorial Vn se numeste ortonormata daca vectorii bazei sunt doi câte doi ortogonali si de marime unitara, adica:
![]()
![]()
![]() = δ km, (6)
= δ km, (6)
unde δ km sunt simbolurile lui Kronecker.
δ km = 1 pentru k = m
δ km = 0 pentru k ≠ m
T. Daca ![]() este o baza ortonormata a lui V
atunci produsele tensoriale (
este o baza ortonormata a lui V
atunci produsele tensoriale (![]()
![]() ) k, m = 1, 2, 3
formeaza o baza a lui L.
) k, m = 1, 2, 3
formeaza o baza a lui L.
În continuare, conform teoremei
anterioare, aratam ca orice tensor T L poate fi scris ca o combinatie
liniara a tensorilor (![]()
![]() ). Întrucât T
). Întrucât T![]() V este un vector din V el se poate scrie în mod unic ca o
combinatie liniara a vectorilor unei baze din V de exemplu,
V este un vector din V el se poate scrie în mod unic ca o
combinatie liniara a vectorilor unei baze din V de exemplu,![]()
T![]() = T km
= T km ![]() (7)
(7)
Atunci în baza relatiilor (8-10)
![]()
![]()
![]() = δ km (8)
= δ km (8)
(![]()
![]() )
)![]() =
= ![]() (
(![]()
![]()
![]() ),
), ![]()
![]() V (9)
V (9)
(![]() +
+![]() )
)![]() = (
= (![]()
![]() +
+ ![]()
![]() ) (10)
) (10)
avem
pentru ![]()
![]() V urmatoarea ecuatie
V urmatoarea ecuatie
(T - T km ![]()
![]() )
) ![]() = T - T km
= T - T km ![]()
![]() ) us
) us ![]() = (T ks - T
km δ ms ) us
= (T ks - T
km δ ms ) us ![]() = ō (11)
= ō (11)
Relatia (11) fiind
valabila pentru ![]()
![]() V rezulta ca: T - T km
V rezulta ca: T - T km ![]()
![]() = ō si în
plus se obtine tocmai relatia ce dovedeste ca T poate fi scris ca o combinatie
liniara de vectorii bazei (
= ō si în
plus se obtine tocmai relatia ce dovedeste ca T poate fi scris ca o combinatie
liniara de vectorii bazei (![]()
![]() ) din L si anume (12)
) din L si anume (12)
T = T km ![]()
![]() (12)
(12)
Marimile T km se numesc componentele tensorului T în baza .
Ultima relatie se poate scrie dezvoltat.
T T11
![]()
![]() + T12
+ T12 ![]()
![]() + T13
+ T13 ![]()
![]() +
+
+ T21
![]()
![]() + T22
+ T22 ![]()
![]() + T23
+ T23 ![]()
![]() + (13)
+ (13)
+ T31
![]()
![]() + T32
+ T32 ![]()
![]() + T33
+ T33 ![]()
![]()
Componentele tensorului T în baza se pot de asemenea dispune într-o matrice patratica de ordinul 3.
T = T km = 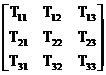 (14)
(14)
T = TT = 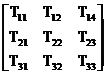 =
= 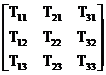 (15)
(15)
D. Urma unui tensor este o aplicatie liniara
definita pe L → ![]()
tr : L → ![]()
tr (![]()
![]() ) =
) = ![]()
![]()
![]() ,
, ![]()
![]() ,
,![]() V (16)
V (16)
Prin urmare tr T = tr( T km ![]()
![]() ) = T km tr
(
) = T km tr
(![]()
![]() ) = T km δ km =
) = T km δ km =
= Tmm = T11 + T22 + T33 (Regula lui Einstein)
Regula lui Einstein prevede ca atunci când doi indici dintr-un monom se repeta, se va face sumarea termenilor obtinuti dând indicilor toate valorile posibile,de exemplu,în cazul anterior m=1,2,3
T ![]() =
= ![]()
![]() (18)
(18)
Observatii O valoare proprie se mai numeste valoare caracteristica sau principala. Un vector propriu de marime unitara se numeste directie principala.
T ![]() -
- ![]()
![]() = ō (T -
= ō (T - ![]() 1)
1) ![]() = ō,
= ō,
relatie vectoriala ce se poate scrie pe componente astfel
(T km - ![]() δ km) um = o (19)
δ km) um = o (19)
Acest sistem (19) de trei ecuatii liniare si omogene admite o solutie nebanala l satisface ecuatia algebrica de gradul 3(ecuatia caracteristica), obtinuta în urma dezvoltarii determinantului urmator:
Det T km - ![]() δ km =
δ km = 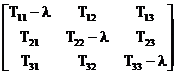 =
=
= ( T11
- ![]() )
)  - T12
- T12  + T13
+ T13  =
=
= (T11
- ![]() ) [(T22 -
) [(T22 - ![]() ) (T33 -
) (T33 - ![]() ) – T23 T32] – T12 [ T21
(T33 -
) – T23 T32] – T12 [ T21
(T33 - ![]() ) - T23T31] +
) - T23T31] +
+ T13
[T21T32 – (T22 - ![]() )T31 =
)T31 =
= (T11
- ![]() ) [ (T22T33 -
) [ (T22T33 - ![]() T33 -
T33 - ![]() T22 +
T22 + ![]() 2) – T23T32 ] – T12
[T21T33 - T21
2) – T23T32 ] – T12
[T21T33 - T21 ![]() - T23T31]
+ T13 [T21T32
– T22T31 +
- T23T31]
+ T13 [T21T32
– T22T31 + ![]() T31] =
T31] =
= T11T22T33
– ![]() T11T33 -
T11T33 - ![]() T11T22
+
T11T22
+ ![]() 2T11 -
2T11 - ![]() T22T33
+
T22T33
+ ![]() 2T33 +
2T33 + ![]() 2T22 -
2T22 - ![]() 3 – T11T23T32 +
3 – T11T23T32 +![]() T23T32 – T12T21T33 +
T23T32 – T12T21T33 + ![]() T12T21
+ T12T23T31 + T13T21T32
– T13T22T31 +
T12T21
+ T12T23T31 + T13T21T32
– T13T22T31 + ![]() T13T31
=
T13T31
=
= - ![]() 3 +
3 + ![]() 2 (T11 + T22 + T33)
-
2 (T11 + T22 + T33)
- ![]() (T11T33
+ T11T22 + T22T33 + T23T32
+ T12T21 + T13T31) + T11T22T33
+ T13T21T32 – T11T23T32
– T12T21T33 + T12T23T31=0
(T11T33
+ T11T22 + T22T33 + T23T32
+ T12T21 + T13T31) + T11T22T33
+ T13T21T32 – T11T23T32
– T12T21T33 + T12T23T31=0
Ecuatie ce se poate rescrie sub forma:
![]() 3 - IT
3 - IT ![]() 2 + IIT
2 + IIT ![]() - IIIT = 0 (20)
- IIIT = 0 (20)
unde
IT = T11 + T22 + T33 = tr T (21)
IIT =
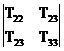 +
+  +
+  (22)
(22)
IIIT =
det T =  (23)
(23)
IT, IIT, IIIT se numesc invariantii lui T, deoarece cele trei valori principale ale unui tensor simetric T si anume(![]() 1,
1,![]() 2,
2,![]() 3) nu depind de alegerea bazei din V si prin
urmare coeficientii ecuatiei cubice în
3) nu depind de alegerea bazei din V si prin
urmare coeficientii ecuatiei cubice în ![]() (20) vor fi
de asemenea invarianti fata de schimbarea bazei în V
(20) vor fi
de asemenea invarianti fata de schimbarea bazei în V
T. (Teorema de descompunere spectrala)
Daca T este un tensor simetric (T
= TT ) din L atunci
exista o baza ortonormata a lui V si trei valori proprii (nu neaparat
distincte) ![]() 1 ,
1 , ![]() 2,
2, ![]() 3, ale lui T a.î.
3, ale lui T a.î.
T ![]() =
= ![]() k
k ![]() k = 1, 2,
3. (fara sumare)
k = 1, 2,
3. (fara sumare)
T = ![]() 1
1 ![]()
![]() +
+ ![]() 2
2 ![]()
![]() +
+ ![]() 3
3 ![]()
![]() (24)
(24)
T = 
Din ecuatia caracteristica cu ajutorul relatiilor lui Vičte rezulta, tinând seama de (24), urmatoarele expresii pentru invarianti
IT = ![]() +
+ ![]() +
+ ![]()
IIT = ![]()
![]() +
+ ![]()
![]() +
+ ![]()
![]() (25)
(25)
IIIT = ![]()
![]()
![]()
2 Tensorul tensiunii
Fie un corp C asupra caruia
actioneaza forta exterioara f. Pe lânga forta exterioara exista
interactiuni între diferite parti ale corpului C, care sunt o
consecinta a fortelor interatomice ce actioneaza în
corpul C. Pentru a descrie aceste forte interne, Cauchy a presupus ca
interactiunea dintre doua parti ale corpului ce au o
frontiera comuna este echivalenta cu o distributie continua
de forte de suprafata pe aceasta frontiera, care au
aceeasi natura cu fortele externe de suprafata si
care depind numai ![]() si de normala la
frontiera,
si de normala la
frontiera, ![]() . Aceste forte, raportate la unitatea de arie, se numesc
vectori ai tensiunii si sunt reprezentate prin simbolul
. Aceste forte, raportate la unitatea de arie, se numesc
vectori ai tensiunii si sunt reprezentate prin simbolul ![]() . Vectorul tensiunii depinde prin ipoteza numai de
. Vectorul tensiunii depinde prin ipoteza numai de ![]() si de
directia normalei
si de
directia normalei ![]() la suprafata de separare pe care
actioneaza.
la suprafata de separare pe care
actioneaza.
Tensorul T (![]() ) L este tensorul tensiunii a lui
Cauchy daca transforma un versor
) L este tensorul tensiunii a lui
Cauchy daca transforma un versor ![]() în vectorul tensiunii
în vectorul tensiunii ![]() (
(![]() ,
,![]() ) ce actioneaza în punctul
) ce actioneaza în punctul ![]() pe o suprafata a
carei normala în
pe o suprafata a
carei normala în ![]() are versorul
are versorul ![]() .
.
Semnificatia fizica a lui T reiese din relatia:
![]() (
(![]() ,
,![]() ) = T (
) = T (![]() )
)![]() (26)
(26)
Daca tensorul T L este tensorul lui Cauchy al tensiunii T = T (![]() ) atunci componentele
diagonale se numesc tensiuni normale, iar cele nediagonale se numesc tensiuni
tangentiale.
) atunci componentele
diagonale se numesc tensiuni normale, iar cele nediagonale se numesc tensiuni
tangentiale.
Tensiunile normale pozitive corespund unei întinderi, iar tensiunile normale negative unei compresiuni pe când semnul atribuit tensiunilor tangentiale nu are o semnificatie intrinseca.
Întrucât tensorul Cauchy T este simetric, ceea ce reiese din ecuatia de bilant a momentului cinetic, el admite conform teoremei de descompunere spectrala trei valori proprii reale distincte sau egale.
În cele ce urmeaza denumim aceste valori proprii tensiuni
principale si le notam ![]() ,
, ![]() ,
, ![]() iar cu
iar cu ![]() ,
, ![]() ,
, ![]() notam trei
directii principale ale lui T
care formeaza o baza ortonormata în punctul
notam trei
directii principale ale lui T
care formeaza o baza ortonormata în punctul ![]() considerat.
considerat.
T = ![]()
![]()
![]() +
+ ![]()
![]()
![]() +
+ ![]()
![]()
![]() (27)
(27)
de unde se vede ca în baza tensiunile tangentiale sunt nule iar matricea componentelor tensorului tensiunii are forma diagonala.
T = 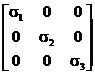
Deci ![]() (
(![]() ,
,![]() ) = T (x)
) = T (x) ![]() = T (x)
= T (x) ![]()
![]() =
=
= ![]()
![]() (
(![]()
![]()
![]() ) +
) + ![]()
![]() (
(![]()
![]()
![]() ) +
) + ![]()
![]() (
(![]()
![]()
![]() ) =
) =
= ![]()
![]()
![]()
![]() (n1
(n1 ![]() + n2
+ n2 ![]() + n3
+ n3 ![]() )
)
+ ![]()
![]()
![]()
![]() (n1
(n1 ![]() + n2
+ n2 ![]() + n3
+ n3 ![]() )
)
+ ![]()
![]()
![]()
![]() (n1
(n1 ![]() + n2
+ n2 ![]() + n3
+ n3 ![]() )
)
= ![]() n1
n1 ![]() +
+ ![]() n2
n2 ![]() +
+ ![]() n3
n3 ![]()
unde n1, n2, n3 sunt componentele lui
![]() în baza , deci în particular
în baza , deci în particular
![]() (
(![]() ,
, ![]() ) =
) = ![]()
![]() =
= ![]()
![]() +
+ ![]()
![]() +
+ ![]()
![]() (28)
(28)
ceea ce arata ca pe elementele de suprafata normale pe o directie principala vectorul tensiunii este dirijat dupa acea directie principala.
3. Tensiuni tangentiale extreme
![]()
![]()
![]()
![]()
![]()
![]()
![]()


Figura 1 Descompunerea vectorului tensiunii
![]() din punctul x al unei suprafete într-o componenta
normala si una tangentiala la suprafata
din punctul x al unei suprafete într-o componenta
normala si una tangentiala la suprafata
Avem: ![]() =
= ![]() -
- ![]() (29)
(29)
![]() =
= ![]()
![]() = (
= (![]() n1
n1![]() +
+![]() n2
n2![]() +
+![]() n2
n2![]() ) (
) (![]() n1
n1![]() +
+![]() n2
n2![]() +
+![]() n2
n2![]() ) =
) =
=
![]()
![]() +
+![]()
![]() +
+![]()
![]() (30)
(30)
![]() =
= ![]()
![]() = (
= (![]() n1
n1![]() +
+ ![]() n2
n2![]() +
+ ![]() n3
n3![]() ) (n1
) (n1![]() + n2
+ n2![]() + n3
+ n3![]() ) =
) =
=
![]()
![]() +
+ ![]()
![]() +
+ ![]()
![]() (31)
(31)
D. Marimea sau intensitatea unui vector ![]() este obtinuta din relatia
este obtinuta din relatia
![]() =
= ![]() (32)
(32)
si
atunci avem pentru ![]() urmatoarea
expresie:
urmatoarea
expresie:
![]() =
= ![]()
![]() +
+ ![]()
![]() +
+ ![]()
![]() - (
- (![]()
![]() +
+ ![]()
![]() +
+ ![]()
![]() )2
)2
Ne punem acum problema determinarii extremelor locale
ale functiei ![]() cu conditia suplimentara:
cu conditia suplimentara:
![]() =
= ![]() +
+ ![]() +
+ ![]() =
= ![]()
![]() = 1 (33)
= 1 (33)
Vom rezolva aceasta problema de extrem cu legaturi folosind metoda multiplicatorilor lui Lagrange.
În acest scop cautam extremele libere ale functiei auxiliare:
n = ![]() -
- ![]() (
( ![]() +
+ ![]() +
+ ![]() - 1) (34)
- 1) (34)
n n ( n1,
n2, n3, ![]() )
)
Anularea derivatelor partiale ale lui n în raport cu n1, n2, n3, conduce la sistemul de ecuatii algebrice
![]()
![]() (35)
(35)
![]()
![]()
Presupunem pentru simplitate ca tensiunile principale sunt distincte si ordonate astfel:

Se constata imediat ca n1, n2, n3 nu pot fi toti nenuli. Astfel, facând diferenta primelor doua si ultimilor doua relatii obtinem:
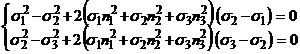 (36)
(36)
sistem care se transforma în
urma împartirii cu (![]() -
-![]() ) a primei ecuatii si cu (
) a primei ecuatii si cu (![]() -
-![]() )a celei de-a doua ecuatii, în urmatoarele
egalitati:
)a celei de-a doua ecuatii, în urmatoarele
egalitati:
![]() (37)
(37)
Ceea ce contrazice ipoteza (![]() <
<![]() <
< ![]() ). În consecinta, cel putin o componenta
a lui
). În consecinta, cel putin o componenta
a lui![]() trebuie sa fie nula.
trebuie sa fie nula.
Daca n1 = 0, n2 0, n3 0 atunci prima ecuatie este satisfacuta, dar ultimile doua pot fi simplificate cu n2, respectiv n3.
Facând diferenta ecuatiilor rezultate si
simplificând cu ![]() -
- ![]() obtinem:
obtinem:
![]()
![]() +
+ ![]()
![]() =
= ![]() (38)
(38)
Dar ![]() +
+ ![]() = 1, ceea ce permite
exprimarea lui
= 1, ceea ce permite
exprimarea lui ![]() in functie de
in functie de ![]()
![]() (1 –
(1 – ![]() ) +
) + ![]()
![]() =
= ![]()
![]() -
- ![]()
![]() +
+ ![]()
![]() =
= ![]() (39)
(39)
![]() (
(![]() -
- ![]() ) =
) =![]() , simplificand cu (
, simplificand cu (![]() -
- ![]() ) se obtine
) se obtine
![]() =
= ![]() =
=![]() ,
, ![]() =
= ![]()
![]() =
=![]()

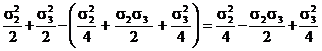
![]() =
= ![]() (40)
(40)
Tratarea cazurilor analoge când n2 = 0, n3 = 0 conduce
în final la trei valori extreme, pe care le notam ![]() ,
, ![]() ,
, ![]() ale tensiunii
principale
ale tensiunii
principale
![]() =
= ![]() ,
, ![]() =
= ![]() ,
, ![]() =
= ![]() (41)
(41)
care actioneaza pe plane cu normala de versori
![]() =
= ![]() ,
, ![]() =
= ![]() ,
, ![]() =
= ![]() , (42)
, (42)
relatiile (42) se obtin deoarece
![]() =
= ![]()
![]() +
+ ![]()
![]() +
+ ![]()
![]()
si de exemplu, pentru n1 = 0 avem
![]() = n2
= n2 ![]() + n3
+ n3 ![]() =
= ![]()
![]() =
= ![]() (43)
(43)
Observam ca planele pe
care actioneaza tensiunile tangentiale extreme bisecteaza
pe cele pe care actioneaza tensiunile principale si în plus,
tinând cont de inegalitatile  ,se obtin
urmatoarele inegalitati
,se obtin
urmatoarele inegalitati
![]() <
< ![]() ,
, ![]() <
< ![]()
Daca n1 = n2 =
0 n3 = 1 tn = 0 ceea ce
arata ca directia corespunzatoare a lui ![]() este una din
directiile principale.
este una din
directiile principale.
3 Tensorul deformatiilor infinitezimale
Pentru a introduce tensorul deformatiilor infinitezimale este necesar mai întâi sa se introduca notiunile de miscare si de deformatie.
![]() (44)
(44)
în care ![]() este fixat
si t variabil
este fixat
si t variabil
(K) – configuratia initiala a corpului corpului C
(k ) – configuratia curenta a corpului C la momentul t
sau: ![]() =
=![]() +
+ ![]()
unde ![]() se numeste
vectorul deplasarii.
se numeste
vectorul deplasarii.



![]()
(K)
P
![]()
![]()
P’
(k)
![]()
Fig.2 Miscarea unui corp deformabil, vectorul deplasarii
Observatie:
Componentele X1, X2, X3 ale lui ![]() se numesc coordonatele materiale sau referentiale, iar
componentele x1, x2, x3 ale lui
se numesc coordonatele materiale sau referentiale, iar
componentele x1, x2, x3 ale lui ![]() se numesc coordonatele
spatiale ale punctului material X.
se numesc coordonatele
spatiale ale punctului material X.
D. Se numeste deformatie o aplicatie de forma (34) la un moment t fixat.
D. Se numeste tensorul deformatiei infinitezimale tensorul simetric de ordinul 2 dat de relatiile:
Ekm = ˝  (45)
(45)
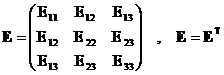 (46)
(46)
 (47)
(47)
Daca notam cu dL distanta dintre punctele materiale ![]() si
si ![]() + d
+ d![]() în configuratia (K) si cu dl distanta dintre
aceleasi puncte în configuratia (k) atunci avem:
în configuratia (K) si cu dl distanta dintre
aceleasi puncte în configuratia (k) atunci avem:
 (48)
(48)
D. Se numeste alungire specifica a vectorului material d![]() raportul :
raportul :
eN = ![]() (49)
(49)
unde ![]() este versorul
este versorul ![]()
Relatiile dintre alungirea specifica în diferite directii si componentele tensorului deformatiei infinitezimale sunt urmatoarele:
e(1) = E11, e(2) = E22, e(3) = E33, (50)
unde (1)
înseamna ca vectorul material elementar avea în configuratia (K)
versorul ![]() (1,0,0), iar pentru (2) avem
(1,0,0), iar pentru (2) avem ![]() (0,1,0) si pentru (3) componentele
(0,1,0) si pentru (3) componentele ![]() (0,0,1).
(0,0,1).
Deci, componentele diagonale ale tensorului deformatiei infinitezimale sunt egale cu alungirile specifice ale vectorilor materiali infinitezimali initial paraleli cu axele de coordonate.
Componentele nediagonale sunt egale cu jumatate din variatiile unghiurilor dintre vectorii materiali inifinitezimali initial paraleli cu axele de coordonate, Figura 3.
Astfel,
cos ![]() , cos
, cos ![]() , cos
, cos ![]() , (51)
, (51)
D. Se numeste dilatare specifica de volum, marimea
e = trE = div ![]() (52)
(52)
în consecinta, o miscare este izocora daca
e = trE = div ![]() =0
=0
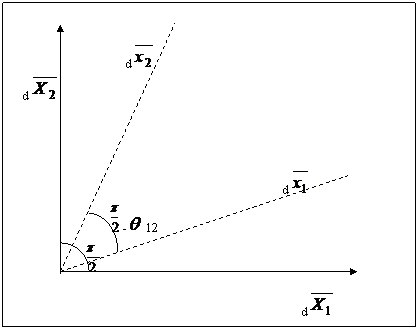
Fig.3 Variatia unghiului dintre vectorii elementari, initial orientati dupa directia axelor(X1, X2), produsa prin deformatie
D. Se numeste tensor de ordinul 3, o aplicatie liniara B a lui V în L
![]() B: V L
B: V L
Notam spatiul vectorial al tensorilor de ordinul 3 cu L3.
D. Se numeste tensor de ordinul 4, o aplicatie liniara C a lui V în L3
![]()
![]() C: V L3
C: V L3
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 280
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved