| CATEGORII DOCUMENTE |
| Agricultura | Asigurari | Comert | Confectii | Contabilitate | Contracte | Economie |
| Transporturi | Turism | Zootehnie |
LIMITELE ARIILOR DE ATRACTIE ALE PIETELOR
Cazul unei marfi omogene
Cazul marfurilor neomogene. Legea lui Reilly
Preturi f.o.b., preturi neutre si preturi de referinta
Aria de atractie a unei piete - suprafata pe care isi poate exercita influenta producatorul ce urmareste sa isi desfaca marfurile pe acea piata.
Cazul unei marfi omogene
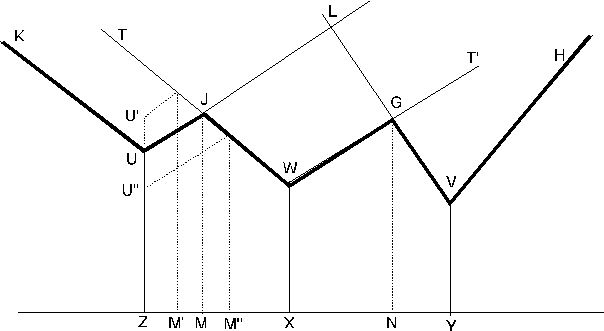
Figura 2.1. Metoda grafica de determinare a ariei de atractie a unei piete (marfuri omogene).
X,Y, Z - trei producatori distribuiti liniar pe piata
XW, YV, ZU - preturile f.o.b. (la poarta fabricii) ale celor trei producatori
Luarea in considerare a cheltuielilor de transport conduce la dreptele WT - WTl, VL - VH si UK - UL, reprezentand preturile f.o.b. plus cheltuielile de transport, direct proportionale cu distanta.
Rezulta: piata lui X = segmentul M N. In interiorul acestui segment pretul f.o.b. plus cheltuielile de transport pentru marfa produsa de X se situeaza sub nivelul acestora in cazul lui Y sau Z.
Cazul marfurilor neomogene
In cazul marfurilor multiple comportamentul descris da modelul marfurilor individuale omogene este considerat ineficient (implica cheltuieli suplimentare de transport si consum de timp pentru multiplicarea deplasarilor la cumparaturi).
Legea lui Reilly asupra gravitatiei comertului cu amanuntul: un centru tinde sa atraga cumpararile unui consumator individual situat in zona sa de interes direct proportional cu marimea sa (masurata, de regula, prin numarul populatiei) si invers proportional cu patratul distantei dintre ei.
X,Y = doua centre aflate competitie
Z = granita dintre pietele celor doua centre
Z se va situa acolo unde atractia relativa dintre cele doua centre este egala, adica:
![]() =
= ![]() (
2.2.1)
(
2.2.1)
Pentru a-l determina pe z (care se prezinta sub forma distantei pana la X) se presupune ca distanta dintre X si Y este r, iar raportul PX / PY = s .
Atunci, relatia (2.2.1) poate fi rescrisa sub forma:
s = ![]() (2.2.2),
(2.2.2),
de unde rezulta :
z = ![]() r (2.2.3)
r (2.2.3)
Caz particular: daca s = 1
(adica X si Y au aceeasi marime), atunci z = ![]() r (granita dintre
cele doua piete se situeaza la mijlocul distantei dintre cele doua centre).
r (granita dintre
cele doua piete se situeaza la mijlocul distantei dintre cele doua centre).
Aplicatie: PX = 270000 locuitori
PY = 30000 locuitori
r = 60 km
Rezulta: z = 45 km (departare de X)
Preturi f.o.b., preturi neutre si preturi de referinta
R

Figura 2.2. Preturi f.o.b., preturi neutre si preturi de referinta.
AB = piata liniara, cu doi producatori, X si Y
Pretul f.o.b.: XW si YV (pretul la poarta fabricii pentru X, respectiv Y)
Luarea in calcul si a cheltuielilor de transport conduce la dreptele WT - WTl pentru X, respectiv VL - VH pentru Y.
Pretul neutru: OOl (pretul f.o.b. care maximizeaza profitul plus cheltuielile de transport medii estimate). In cazul lui X, prin acest sistem de preturi sunt discriminati cumparatorii din interiorul segmentului PPl (acestia platesc mai mult decat in sistemul f.o.b.)
Pretul de referinta: este stabilit indiferent de situarea reala a producatorului sau de cheltuielile reale de transport.
Daca X = punctual de referinta, cumparatorul din Q va plati QS, chiar daca cumpara de la Y.
Se observa ca QS > QR. RS = "transportul - fantoma" plus diferenta de cost de productie dintre X si Y.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1398
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved