| CATEGORII DOCUMENTE |
| Agricultura | Asigurari | Comert | Confectii | Contabilitate | Contracte | Economie |
| Transporturi | Turism | Zootehnie |
Consumator: agent economic care are functia de a consuma bunuri economice, criteriul sau de comportament economic fiind maximizarea utilitatii consumului
Definitie: utilitatea unui bun economic este data de capacitatea acestuia de a satisface o nevoie economica stabilita, la un nivel considerat acceptabil de catre consumator
utilitatea reprezinta satisfactia subiectiva resimtita la consumarea bunului
Exista doua teorii privind utilitatea bunurilor (a consumului de bunuri):
Teoria utilitatii cardinale: fiecarui bun i se poate asocia un numar numit numar de utilitate, ceea ce face ca bunurile sa poata fi comparate cantitativ intre ele
aceasta intrucat utilitatea este obiectiva, invariabila, fiind data de caracteristicile bunului
cel mai uzual numar de utilitate este pretul
teoria are doua inconveniente:
presupunerea constantei valorii unitatii monetare - presupunere falsa
utilitatea unui cos de bunuri este egala cu suma utilitatilor individuale ale bunurilor din cos - presupunere falsa
Fie un bun economic, x. O functie notata U=U(x) este functie de utilitate daca indeplineste urmatoarele conditii, cumulativ:
1. x > 0 : bunul economic este real
2. U'(x) > 0 : utilitatile individuale (ale fiecarei unitati din bun) sunt aditive
U''(x) < 0 : satisfactia creste incetinit la cresterea consumului (legea I a lui Gossen)
4. U(0) = 0 : utilitatea are sens numai la consumul bunului economic (obs.: cu exceptia cazului abstinentilor)
NB : Conditiile functiei de utilitate trebuie indeplinite pentru fiecare bun economic, in cazul in care este vorba nu despre un bun individual ci despre un cos de bunuri x, y, z, .

Tema de seminar: sa se scrie conditiile
functiei de utilitate pentru cazul unui cos
de doua bunuri economice
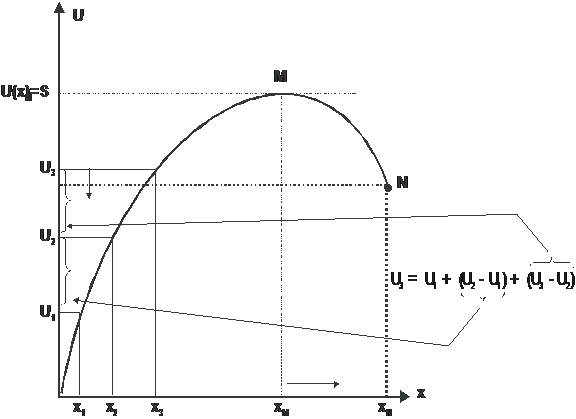
Figura 7: Curba utilitatii totale. Aditivitatea utilitatilor individuale
Din forma concava a functiei utilitatii totale rezulta ideea ca sporul de utilitate totala este descrescator
Definitie: utilitatea marginala (Um) reprezinta modificarea utilitatii totale antrenata de modificarea cu o unitate a cantitatii consumate din bun
![]()
![]() Mod de calcul sau, in cazul continuu,
Mod de calcul sau, in cazul continuu,
Analiza calitativa a utilitatii marginale:
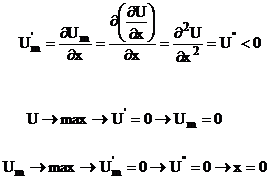
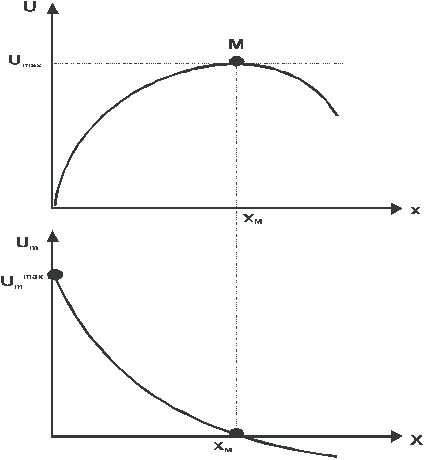
Figura 8: Curba utilitatii marginale
Utilitatea marginala sta la baza formarii pretului bunurilor economice
Mecanismul de formare a pretului de tranzactie se bazeaza pe coincidenta valorica dintre utilitatea marginala a monedei (la care se renunta) si utilitatea marginala a bunului economic (care este dorit)
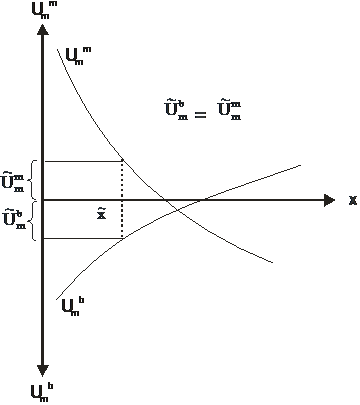
Figura 9: Mecanismul tranzactiei economice pe baza utilitatii marginale
Enuntul paradoxului apa-diamant: desi apa este cu mult mai importanta pentru om, fiind cu mult mai utila decat diamantul, acesta este, totusi, cu mult mai scump decat apa
Este un paradox aparent, bazat pe confuzia intre utilitatea totala si utilitatea marginala
Rezolvarea paradoxului
prin introducerea raritatii ca factor de crestere a utilitatii marginale si care ordoneaza bunurile pe axa cantitatilor
pe baza faptului ca pretul este dat de utilitatea marginala si nu de cea totala

Figura 10: Rezolvarea paradoxului apa-diamant
Definitie: Ansamblul punctelor din spatiul bidimensional (x,y) care desemneaza combinatii de consum ce asigura o aceeasi utilitate totala
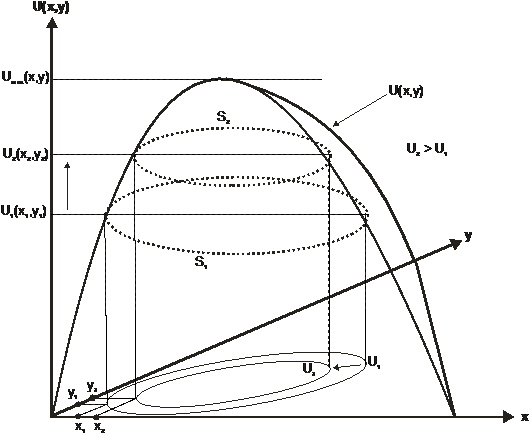
Figura 11: Derivarea curbei de indiferenta pentru cazul a doua bunuri
Curba de indiferenta nu poate avea forma circulara, ea are sens economic, ca ansamblu al alegerilor potentiale ale consumatorului, numai pe zona ei descrescatoare si convexa

Tema de seminar: sa se demonstreze afirmatia de mai sus, pe baza comportamentului rational al consumatorului
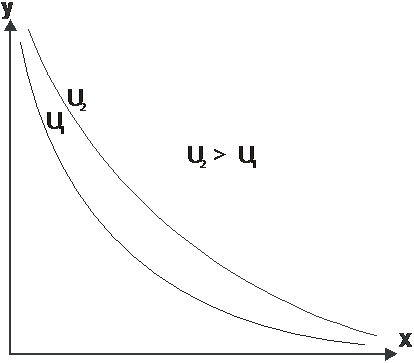
Figura 12: Zona semnificativa economic a curbei de indiferenta
Pe baza definitiei curbei de indiferenta, se poate deduce ecuatia acesteia:
![]()
Din ultima relatie se poate deduce un indicator economic foarte important pentru decizia consumatorului si anume rata marginala de substitutie (Rms):
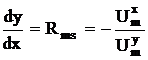
Definitie: Rata marginala de substitutie (Rms) arata cu cate unitati se modifica cantitatea consumata dintr-un bun atunci cand cantitatea consumata din bunul alternativ se modifica cu o unitate, in sens contrar, asa incat utilitatea totala sa nu se modifice (decizia sa ramana pe curba de indiferenta)
Din punct de vedere grafic, rata marginala de substitutie poate fi reprezentata astfel:

Figura 13: Imaginea grafica a ratei marginale de substitutie a bunurilor

Tema de seminar: sa se arate ca doua curbe de indiferenta nu se pot intersecta
Continut: Suma monetara alocata achizitionarii de bunuri economice
Definitie: Ansamblul punctelor din spatiul bidimensional (x,y) care reprezinta decizii de consum ce epuizeaza complet suma monetara alocata consumului de bunuri economice
Fie doua bunuri economice, x, respectiv y, avand preturile de tranzactionare px, respectiv py. Vom presupune ca x si y desemneaza, totodata si cantitatile achizitionate din cele doua bunuri. De asemenea, admitem, pentru moment, ca preturile de tranzactie ale celor doua bunuri sunt constante
Fie B bugetul consumatorului. Admitem, pentru moment, ca si bugetul este constant
Atunci, conform continutului bugetului consumatorului, se poate scrie:
![]() , sau:
, sau:
 , numita
ecuatia bugetului consumatorului, unde:
, numita
ecuatia bugetului consumatorului, unde:
 se numeste pretul relativ
al bunurilor x si y
se numeste pretul relativ
al bunurilor x si y

Figura 14: Linia bugetului consumatorului si deciziile semnificative economic
Consumatorul va alege in acel punct care satisface, simultan, restrictia sa bugetara (bugetul consumatorului) si curba sa de indiferenta
Rezulta ca, din punct de vedere grafic, decizia se va lua in punctul de tangenta dintre linia de buget si curba de indiferenta:

Figura 14: Alegerea optima (grafica) a consumatorului
Din punct de vedere analitic, trebuie rezolvat sistemul de ecuatii format din ecuatia bugetului consumatorului si ecuatia curbei de indiferenta:

Diferentiind ecuatia bugetului in raport de x si y, obtinem:

Eliminand pe ![]() intre cele doua
ecuatii ale sistemului, obtinem, succesiv:
intre cele doua
ecuatii ale sistemului, obtinem, succesiv:
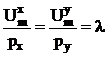
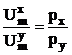
unde ![]() se numeste
multiplicator Lagrange
se numeste
multiplicator Lagrange
![]()
al consumului si exprima numarul de unitati cu care se modifica utilitatea totala a consumatorului atunci cand bugetul sau se modifica cu o unitate
Asadar, conditia de optim analitic al consumatorului este data de egalitatea rapoartelor dintre utilitatea marginala a fiecarui bun si pretul sau (a doua lege a lui Gossen)
Sa demonstram semnificatia economica a multiplicatorului Lagrange, in cazul a n bunuri economice:
Fie bunurile x1, x2, ., xn , cu preturile, respectiv p1, p2, ., pn.
Functia de utilitate aferenta va fi: U(x1, x2, ., xn).
Bugetul consumatorului este: ![]()
Intrucat preturile sunt constante, rezulta ca orice
modificare in buget se regaseste in modificarea
cantitatilor de bunuri achizitionate, adica: ![]() .
.
Functia Lagrange care maximizeaza utilitatea in conditiile restrictiei bugetare este:
![]()
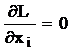 Conditia de maximizare cere
ca , pentru orice i,
adica:
Conditia de maximizare cere
ca , pentru orice i,
adica:
![]()
Modificarea utilitatii totale este:
![]() ,
,
adica definitia prezentata mai sus.
 Tema de seminar: sa se refaca demonstratia semnificatiei economice a
multiplicatorului Lagrange pentru cazul a doua bunuri
Tema de seminar: sa se refaca demonstratia semnificatiei economice a
multiplicatorului Lagrange pentru cazul a doua bunuri
Pentru px respectiv py constante si buget variabil, ecuatia bugetului conduce la o familie de drepte paralele (cu aceeasi panta, respectiv pretul relativ, pr=px/py=const.)
Fiecare linie de buget din familie conduce la un optim, iar ansamblul acestor puncte de optim genereaza magistrala consumului (traiectoria consumului)
Intr-adevar, din ![]() , pentru preturi constante si buget variabil,
rezulta
, pentru preturi constante si buget variabil,
rezulta ![]() constant, iar
constant, iar ![]() variabil
variabil
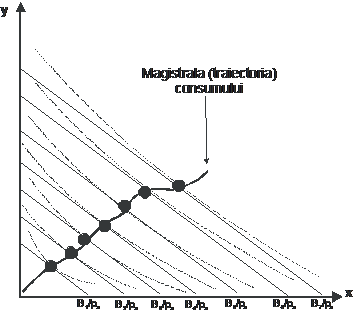
Figura 15: Imaginea grafica a magistralei consumului
Definitie Magistrala consumului este curba care uneste punctele de optim ale consumatorului la preturi constante si buget variabil
Magistrala consumului are forme diferite pentru cele trei categorii de bunuri de consum (curbele Engel):
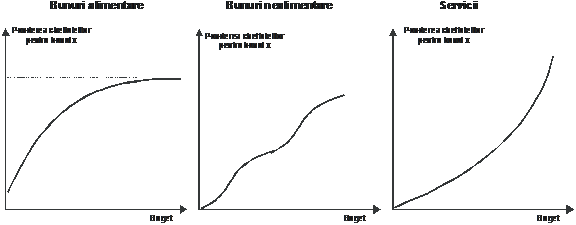
Figura 16: Curbele Engel ale consumului
![]() Daca bugetul este constant iar
preturile variaza (pentru simplificare vom pastra pe py
constant si vom varia doar pe px), din ecuatia bugetului
rezulta ca, pentru diverse valori ale lui px vom avea o
familie de bugete cu termen liber (B/py) fix si pante (-px/py)
variabile
Daca bugetul este constant iar
preturile variaza (pentru simplificare vom pastra pe py
constant si vom varia doar pe px), din ecuatia bugetului
rezulta ca, pentru diverse valori ale lui px vom avea o
familie de bugete cu termen liber (B/py) fix si pante (-px/py)
variabile
Variatia preturilor la bugete constante conduce la doua efecte economice foarte importante pentru studiul comportamentului consumatorului:
efectul de substitutie (Es)
efectul de venit (Ev)
Cele doua efecte economice definesc patru categorii de bunuri economice (in functie de semnul algebric si de marimea absoluta a lor):
bunuri normale
bunuri superioare
bunuri inferioare
bunuri Giffen
Cazul bunurilor normale
Daca px scade, panta liniei bugetului scade si aceasta devine mai plata (se va cumpara mai mult x)
Mentinerea pretului relativ constant se obtine prin construirea unei drepte paralele la noua linie de buget
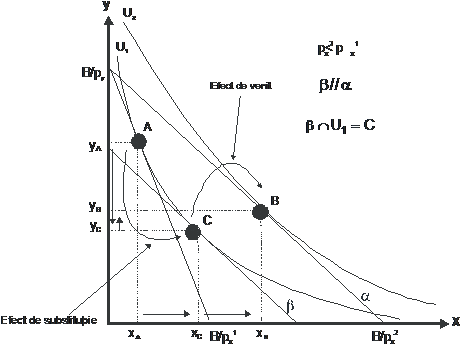
Figura 17: Efectul de substitutie si efectul de venit. Cazul bunurilor normale
Definitie efect de substitutie: modificarea structurii de consum la modificarea preturilor si la buget constant, cu variatia pretului relativ si cum mentinerea utilitatii totale
mod de calcul: ES = xC - xA
Definitie efect de venit: modificarea cantitatii consumate din ambele bunuri, in acelasi sens, la modificarea preturilor si la buget constant, cu mentinerea pretului relativ si cu variatia utilitatii totale
mod de calcul: EV = xB - xC
Conditia matematica pentru identificarea bunurilor normale:
ES > 0; EV > 0 ; ET = ES + EV > 0 (ET este efectul total)
OBS 1. Daca pretul bunului
x scade, atunci modificarea cantitatii
consumate din ambele bunuri
este de crestere, daca pretul
respectiv creste,
atunci modificarea mentionata este de scadere

Tema de seminar: sa se refaca demonstratia efectului de substitutie si a efectului de venit pentru cazul cresterii pretului bunului x
Cazul bunurilor inferioare
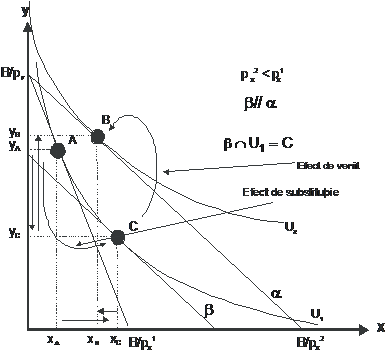
Figura 18: Efectul de substitutie si efectul de venit. Cazul bunurilor inferioare
Conditia matematica de identificare a bunurilor inferioare este:
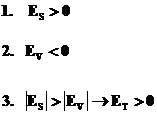
Cazul bunurilor Giffen
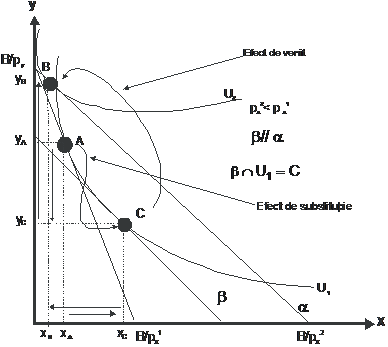
Figura 19: Efectul de substitutie si efectul de venit. Cazul bunurilor Giffen
Conditia matematica de identificare a bunurilor Giffen este:
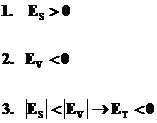
OBS:
Cazul bunurilor superioare este imaginea in oglinda a cazului bunurilor normale (la scaderea pretului bunului analizat, linia de buget isi mareste panta - se va cumpara mai putin din bunul analizat - iar la cresterea pretului, linia de buget isi micsoreaza panta - se va cumpara mai mult din bunul analizat)
 Tema de seminar: Sa se studieze grafic efectul de substitutie si efectul de
Tema de seminar: Sa se studieze grafic efectul de substitutie si efectul de
venit in cazul bunurilor superioare
 Tema de seminar: Sa se refaca demonstratia pentru efectul de
substitutie
Tema de seminar: Sa se refaca demonstratia pentru efectul de
substitutie
si efectul de venit in cazul in care variaza ambele preturi nominale
Daca in analizele precedente s-a stabilit structura optima de consum la un moment dat, este util sa se cerceteze repartizarea unei structuri de consum date, in timp
Fie o structura fixa de consum S
Fie perioadele de timp 1, 2, ., n
Structura fixa de consum aleasa pentru perioada i este Si
Definim functia de utilitate intertemporala: U(S1, S2, ., Sn)
Consumatorul va trebui, deci, sa aleaga nu intre diferite structuri de consum ci o aceeasi structura de consum intre diferite momente de timp
Definim curba de indiferenta intertemporala ca fiind ansamblul punctelor din spatiul bidimensional (S1, S2) care asigura combinatii de consum intertemporal care conduc la aceeasi utilitate totala (vazuta ca utilitate intertemporala)
Sa stabilim ecuatia curbei de indiferenta intertemporala (1) ecuatia intertemporala a bugetului (2), si optimul consumatorului (3) in acest caz
![]()
unde ![]() este rata
marginala de substitutie intertemporala iar
este rata
marginala de substitutie intertemporala iar ![]() este utilitatea
marginala intertemporala a consumului in anul i
este utilitatea
marginala intertemporala a consumului in anul i
![]() Definim rata de arbitraj in
timp:
Definim rata de arbitraj in
timp:
Fie un buget B pentru doi ani, 1 si 2
In momentul 1, consumatorul consuma bunuri in valoare de S1, iar in momentul 2 consuma bunuri in valoare de S2:
![]()
unde cu i s-a notat rata dobanzii bancare. S2 reprezinta ecuatia intertemporala a bugetului
Sistemul de ecuatii pentru optimul consumatorului va fi:

![]()
Diferentiind ecuatia bugetului intertemporal obtinem:
![]() Eliminand raportul
Eliminand raportul ![]() intre ecuatiile
sistemului, rezulta:
intre ecuatiile
sistemului, rezulta:
![]() de unde:
de unde:
care reprezinta conditia de optim intertemporal al consumatorului.
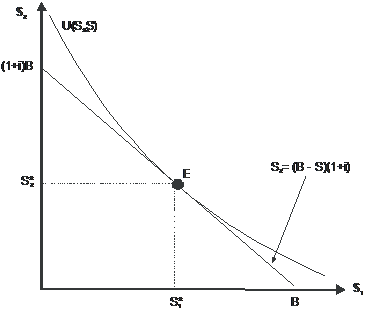
Figura 20: Optimul intertemporal al consumatorului
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2621
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved