| CATEGORII DOCUMENTE |
| Agricultura | Asigurari | Comert | Confectii | Contabilitate | Contracte | Economie |
| Transporturi | Turism | Zootehnie |
| Navigatie |
Aria plutirii, abscisa centrului plutirii, momentele de inertie
longitudinal si transversal ale plutirii.
Daca se considera o plutire oarecare (Fig. 17) atunci fata de sistemul de axe adoptat, aria plutirii se poare calcula cu formula:
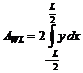 (8.22)
(8.22)
unde
![]() este semilatimea
plutirii la abscisa
este semilatimea
plutirii la abscisa ![]() .
.

Din
considerente de simetrie a conturului plutirii fata de axa ![]() , centrul plutirii
, centrul plutirii ![]() se va gasi pe
aceasta axa, deci
se va gasi pe
aceasta axa, deci ![]() . Abscisa centrului plutirii se calculeaza cu formula:
. Abscisa centrului plutirii se calculeaza cu formula:
![]() (8.23)
(8.23)
in
care ![]() este momentul static al suprafetei plutirii in raport cu
axa
este momentul static al suprafetei plutirii in raport cu
axa ![]() . Cum
. Cum ![]() formula (8.23) se mai
poate scrie:
formula (8.23) se mai
poate scrie:
 (8.24)
(8.24)
Suprafata hasurata din
Fig. 17 este o suprafata elementara de forma unui dreptunghi cu
dimensiunile ![]() si
si ![]() ;
; ![]() . Momentul de inertie al acestei suprafete
elementare in raport cu axa
. Momentul de inertie al acestei suprafete
elementare in raport cu axa ![]() va fi:
va fi:
![]() (8.25)
(8.25)
Momentul
de inertie al intregii plutiri in raport cu axa ![]() se poate scrie:
se poate scrie:
 (8.26)
(8.26)
Rationand
asemanator, momentul de inertie al suprafetei plutirii in
raport cu axa ![]() se scrie:
se scrie:
 (8.27)
(8.27)
Momentul
de inertie al suprafetei plutirii in raport cu axa ![]() (axa paralela cu
(axa paralela cu ![]() ce trece prin centrul plutirii
ce trece prin centrul plutirii ![]() ) se calculeaza aplicand teorema lui Steiner:
) se calculeaza aplicand teorema lui Steiner:
![]() (8.28)
(8.28)
Utilizand relatia (8.24) se poate
calcula abscisa centrului plutirii pentru plutiri succesive situate intre ![]() si planul
corespunzator unui pescaj oarecare, prin urmare se poate construi prin
puncte curba
si planul
corespunzator unui pescaj oarecare, prin urmare se poate construi prin
puncte curba ![]() . Datorita unor proprietati pe care le vom
prezenta in continuare, curbele
. Datorita unor proprietati pe care le vom
prezenta in continuare, curbele ![]() si
si ![]() se vor reprezenta la
aceeasi scara in planul de forme.
se vor reprezenta la
aceeasi scara in planul de forme.
Astfel
cele doua curbe pleaca din acelasi punct pentru ca daca
se trece la limita in relatia (8.12) a lui ![]() gasim:
gasim:
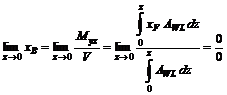
Prin
aplicarea regulii lui L'Hospital se inlatura aceasta
nedeterminare si obtinem ca pentru ![]() .
.
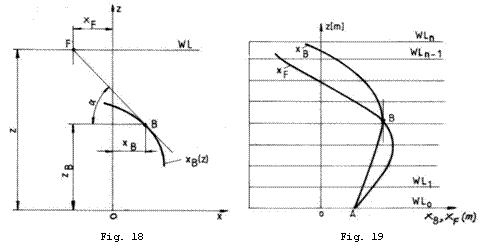
In afara de punctul de pornire ![]() (Fig. 19) cele doua
curbe mai pot avea un punct comun sau nu. Vom demonstra ca daca cele
doua curbe mai au un punct de intersectie, atunci acesta este un
punct de extrem pentru
(Fig. 19) cele doua
curbe mai pot avea un punct comun sau nu. Vom demonstra ca daca cele
doua curbe mai au un punct de intersectie, atunci acesta este un
punct de extrem pentru ![]() (punctul
(punctul ![]() din Fig.19) adica
solutie a ecuatiei
din Fig.19) adica
solutie a ecuatiei
![]() . (8.29)
. (8.29)
Sa evaluam membrul stang al relatiei (8.29):

![]() . (8.30)
. (8.30)
Dar
![]() de unde rezulta ca
de unde rezulta ca
![]() si pe de alta
parte
si pe de alta
parte ![]() . Inlocuind in (8.30) obtinem:
. Inlocuind in (8.30) obtinem:
![]() (8.31)
(8.31)
relatie echivalenta cu:
![]() . (8.32)
. (8.32)
In felul acesta conditia de extrem
(8.29) a functiei ![]() se reduce la:
se reduce la:
![]() (8.33)
(8.33)
ceea ce trebuia demonstrat.
Revenind la centrul de carena ![]() vom observa ca
pentru orice valoare
vom observa ca
pentru orice valoare ![]() a pescajului pozitia
sa este in
a pescajului pozitia
sa este in ![]() , deplasandu-se dupa o curba situata in acest
plan. Pentru a duce ecuatia acestei curbe plecam de la:
, deplasandu-se dupa o curba situata in acest
plan. Pentru a duce ecuatia acestei curbe plecam de la:
![]() sau mai departe
sau mai departe ![]() (8.34)
(8.34)
Tinand cont de relatiile (8.20) si (8.32) rezulta:
![]() (8.35)
(8.35)
Cu
alte cuvinte dreapta ce uneste centrul plutirii ![]() , corespunzator unui anumit pescaj, cu pozitia
centrului de carena
, corespunzator unui anumit pescaj, cu pozitia
centrului de carena ![]() este tangenta la
curba centrelor de carena in punctul respectiv (Fig. 18).
este tangenta la
curba centrelor de carena in punctul respectiv (Fig. 18).
In figura 20 este prezentata curba ariilor plutirilor in doua variante: nava cu fund stelat (Fig. 20, a) si nava cu fund plat (Fig. 20, b).
Aceasta curba ne ofera informatii complete legate de volumul carenei la un anumit pescaj si distributia acestuia pe inaltime. Amintim proprietatile de baza ale acestei curbe:
1). Aria marginita de curba
si axa ![]() reprezinta la
scara desenului volumul carenei corespunzator pescajului considerat:
reprezinta la
scara desenului volumul carenei corespunzator pescajului considerat:
![]() (8.36)
(8.36)

2).
Coeficientul de finete al acestei arii este egal cu coeficientul de finete
prismatic vertical al carenei, ![]() :
:
![]() (8.37)
(8.37)
3). Ordonata centrului de greutate al
ariei marginita de curba si axa ![]() este egala la scara cu cota centrului de carena
este egala la scara cu cota centrului de carena
![]() :
:
 (8.38)
(8.38)
8.3. Ariile sectiunilor transversale.
Curba ariilor sectiunilor transversale.
Considerand o sectiune transversala
prin nava la o distanta ![]() de planul sectiunii
de la mijlocul navei (Fig. 21) atunci aria imersa a acestei sectiuni
se poate calcula cu formula:
de planul sectiunii
de la mijlocul navei (Fig. 21) atunci aria imersa a acestei sectiuni
se poate calcula cu formula:

![]() (8.39)
(8.39)
Daca
se calculeaza aceste arii pentru mai multe sectiuni transversale
(cuple) sa zicem 21, distribuite de la pupa (cupla 0 contine ![]() ) la prova (cupla 20 contine
) la prova (cupla 20 contine ![]() , atunci se va putea reprezenta grafic prin puncte curba
, atunci se va putea reprezenta grafic prin puncte curba ![]() . Se obtine astfel curba ariilor sectiunilor
transversale, care arata ca in Fig. 22.
. Se obtine astfel curba ariilor sectiunilor
transversale, care arata ca in Fig. 22.
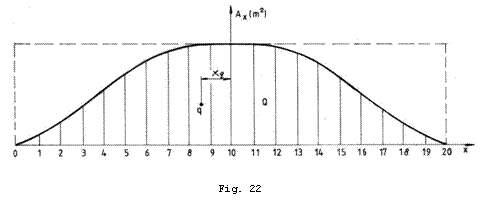
Aceasta curba ne defineste pe deplin volumul carenei si distributia acestuia pe lungimea navei. Evidentiem urmatoarele proprietati ale acestei curbe:
1). Aria marginita de curba
si axa ![]() reprezinta la
scara desenului volumul carenei:
reprezinta la
scara desenului volumul carenei:
 (8.40)
(8.40)
2). Coeficientul de finete al
acestei arii este egal cu coeficientul de finete prismatic longitudinal al
carenei, ![]() :
:
![]() (8.41)
(8.41)
3). Abscisa centrului de greutate al
suprafetei ![]() este egala la
scara cu abscisa centrului de carena
este egala la
scara cu abscisa centrului de carena ![]() :
:
 (8.42)
(8.42)
8.4. Diagrama de carene drepte.
Daca asamblam intr-o singura
diagrama curbele de variatie cu pescajul navei, ale tuturor
elementelor hidrostatice ale carenei despre care am vorbit mai sus, se obtine
diagrama de carene drepte. Aceasta diagrama este intocmita
pentru nava pe carena dreapta, fara inclinari
transversale si longitudinale ![]() ; caz in care singurul parametru care defineste plutirea
este pescajul de calcul
; caz in care singurul parametru care defineste plutirea
este pescajul de calcul ![]() . Din diagrama se obtin in functie de
. Din diagrama se obtin in functie de ![]() urmatoarele marimi:
volumul carenei
urmatoarele marimi:
volumul carenei ![]() ; deplasamentul navei
; deplasamentul navei ![]() ; abscisa
; abscisa ![]() si cota
si cota ![]() a centrului de carena,
abscisa centrului plutirii
a centrului de carena,
abscisa centrului plutirii ![]() , aria plutirii
, aria plutirii ![]() ; momentele de inertie axiale ale plutirii: longitudinal
; momentele de inertie axiale ale plutirii: longitudinal
![]() si transversal
si transversal ![]() , precum si coeficientii de finete
, precum si coeficientii de finete ![]() . Diagrama de carene drepte mai contine de asemenea
curbele de variatie cu pescajul ale razelor metacentrice: transversala
. Diagrama de carene drepte mai contine de asemenea
curbele de variatie cu pescajul ale razelor metacentrice: transversala
![]() si longitudinala
si longitudinala
![]() , despre care vom vorbi in detaliu in Capitolul. III.
, despre care vom vorbi in detaliu in Capitolul. III.

Modul de lucru
cu diagrama de carene drepte rezulta usor daca se studiaza
Fig.23 care reprezinta o varianta de 'Diagrama de carene
drepte'. Astfel pentru un pescaj de calcul fixat ![]() se duce o paralela
la axa absciselor intersectandu-se cu fiecare din curbele enumerate mai sus.
Din punctele de intersectie se coboara perpendiculare pe abscisa
citindu-se valorile acestor marimi la scara lor de reprezentare.
se duce o paralela
la axa absciselor intersectandu-se cu fiecare din curbele enumerate mai sus.
Din punctele de intersectie se coboara perpendiculare pe abscisa
citindu-se valorile acestor marimi la scara lor de reprezentare.
Razele metacentrice: transversala ![]() si longitudinala
si longitudinala
![]() , se calculeaza cu formulele:
, se calculeaza cu formulele:
![]() (8.43)
(8.43)
![]() (8.44)
(8.44)
8.5. Formulele empirice pentru calculul unor marimi hidrostatice pe carene drepte.
Pentru estimarea rapida a unor elemente hidrostatice pe carene drepte se folosesc deseori formule empirice sau semiempirice bazate pe prelucrarea statistica a datelor existente sau pe inlocuirea curbelor reale din diagrama de carene drepte cu curbe apropiate ca forma, descrise de ecuatii analitice.
Redam mai jos cateva formule de calcul a unor marimi hidrostatice:
a) Cota centrului de carena ![]()
O astfel de formula va fi de tipul:
![]() (8.44)
(8.44)
unde
![]() este un coeficient
care depinde de coeficientul de finete bloc
este un coeficient
care depinde de coeficientul de finete bloc ![]() , respectiv al ariei plutirii
, respectiv al ariei plutirii ![]() .
.
![]() formula Pozdiunin; (8.45)
formula Pozdiunin; (8.45)
![]() formula Vlasov; (8.46)
formula Vlasov; (8.46)
![]() formula
Norman; (8.47)
formula
Norman; (8.47)
b) Abscisa centrului de carena ![]()
![]() formula Vlasov; (8.48)
formula Vlasov; (8.48)
![]() formula Norman; (8.49)
formula Norman; (8.49)
echivalenta cu:
![]() (8.50)
(8.50)
In formulele de mai sus, ![]() si
si ![]() sunt volumele de carena
corespunzator jumatatilor prova si pupa, masurate
de la jumatatea lungimii navei si
sunt volumele de carena
corespunzator jumatatilor prova si pupa, masurate
de la jumatatea lungimii navei si ![]() coeficientii de
finete prismatic longitudinal aferenti. Prin urmare:
coeficientii de
finete prismatic longitudinal aferenti. Prin urmare:
![]() (8.51)
(8.51)
![]() (8.52)
(8.52)
c) Abscisa centrului plutirii ![]()
![]() formula Vlasov; (8.53)
formula Vlasov; (8.53)
![]() formula Norman; (8.54)
formula Norman; (8.54)
echivalenta cu:
![]() (8.55)
(8.55)
In formulele de mai sus, ![]() si
si ![]() sunt ariile plutirii
corespunzator jumatatilor prova si pupa, iar
sunt ariile plutirii
corespunzator jumatatilor prova si pupa, iar ![]() coeficientii de
finete ai acestor arii. Asadar:
coeficientii de
finete ai acestor arii. Asadar:
![]() (8.56)
(8.56)
![]() (8.57)
(8.57)
d) Razele metacentrice: transversala
![]() si longitudinala
si longitudinala
![]()
Pentru cele doua marimi se propun formule de tipul:
![]() (8.58)
(8.58)
![]() (8.59)
(8.59)
Se demonstreaza foarte usor ca
pentru cazul unui ponton paralelipipedic, coeficientii ![]() si
si ![]() sunt egali respectiv
cu:
sunt egali respectiv
cu:
![]() (8.60)
(8.60)
![]() formula Van-der-Fleet; (8.61)
formula Van-der-Fleet; (8.61)
unde
![]() este un coeficient
cuprins intre 11,2 si 11,9 care tine cont de forma plutirii.
este un coeficient
cuprins intre 11,2 si 11,9 care tine cont de forma plutirii.
![]() formula Norman; (8.62)
formula Norman; (8.62)
![]() formula Vlasov; (8.63)
formula Vlasov; (8.63)
![]() formula Van-der-Fleet; (8.64)
formula Van-der-Fleet; (8.64)
![]() formula Norman; (8.65)
formula Norman; (8.65)
![]() formula Vlasov. (8.66)
formula Vlasov. (8.66)
9. Calculul practic de carene drepte. Metode numerice.
Atat in timpul proiectarii navei, cat si in decursul exploatarii ei, apare necesitatea determinarii unor caracteristici cum sunt: arii, volume, momente de inertie, momente statice, etc. prezentate mai jos:
1. Aria plutirii (vezi formula 8.22)
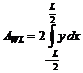
2. Ariile sectiunilor transversale (vezi formula 8.39)
![]()
3. Volumul carenei (vezi formulele 8.2 si 8.3)

4. Momentele statice ale volumului carenei in raport cu planele sistemului de coordonate (vezi formulele 8.8 si 8.10)

![]()
5. Momentul static al ariei plutirii (vezi formula 8.24)

6. Momentele de inertie ale suprafetei plutirii (vezi formulele 8.26 si 8.27)


Determinarea acestor marimi implica rezolvarea unor integrale de forma:
 sau
sau ![]() .
.
Daca functiile ![]() , respectiv
, respectiv ![]() ar fi cunoscute,
atunci integralele
ar fi cunoscute,
atunci integralele ![]() si
si ![]() ar putea fi calculate
analitic. Cum formele navei nu sunt date analitic, ele fiind definite discret,
se apeleaza la integrarea numerica a integralelor
ar putea fi calculate
analitic. Cum formele navei nu sunt date analitic, ele fiind definite discret,
se apeleaza la integrarea numerica a integralelor ![]() si
si ![]() .
.
Principiul de integrare numerica
se bazeaza pe faptul ca ![]() reprezinta aria
cuprinsa intre graficul functiei
reprezinta aria
cuprinsa intre graficul functiei ![]() , axa
, axa ![]() si dreptele
si dreptele ![]() si
si ![]() .
.
Valoarea aproximativa a integralei
se obtine daca se divide intervalul ![]() in portiuni mai mici si apoi se insumeaza aria
fiecarei fasii obtinute.
in portiuni mai mici si apoi se insumeaza aria
fiecarei fasii obtinute.
Formula generala de calcul a
integralei ![]() printr-o metoda
numerica este:
printr-o metoda
numerica este:
![]() (9.1)
(9.1)
unde
![]() cu
cu ![]() .
.
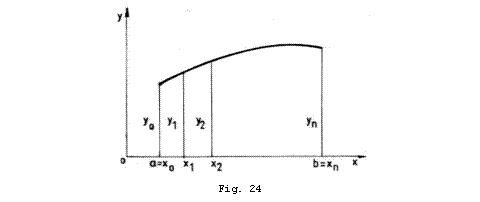
Daca presupunem curba de forma
matematica polinom de gradul ![]() :
: ![]() atunci metodele de
integrare numerica se pot clasifica dupa cum urmeaza:
atunci metodele de
integrare numerica se pot clasifica dupa cum urmeaza:
1) metode in care intervalul ![]() se divide in parti egale avand capetele
se divide in parti egale avand capetele ![]() si
si ![]() iar problema este sa
gasim coeficientii
iar problema este sa
gasim coeficientii ![]() astfel incat relatia
(9.1) sa exprime aria cautata (metoda trapezelor si metoda
Simpson);
astfel incat relatia
(9.1) sa exprime aria cautata (metoda trapezelor si metoda
Simpson);
2) metode in care ![]() si problema consta
in localizarea intervalelor din conditia de precizie maxima (metoda
Cebasev);
si problema consta
in localizarea intervalelor din conditia de precizie maxima (metoda
Cebasev);
3) metode in care problema consta
atat in determinarea coeficientilor ![]() cat si in localizarea
intervalelor din conditia de precizie maxima (metoda Gauss).
cat si in localizarea
intervalelor din conditia de precizie maxima (metoda Gauss).
Metoda trapezelor
Aceasta metoda presupune ca
poate inlocui curba dintre doua ordonate consecutive cu o dreapta de
ecuatie ![]() (Fig. 25) si se
poate aproxima aria patrulaterului curbiliniu
(Fig. 25) si se
poate aproxima aria patrulaterului curbiliniu ![]() cu aria trapezului
cu aria trapezului ![]() avand valoarea:
avand valoarea:
![]()

Prin generalizare obtinem:
![]() (9.2)
(9.2)
unde
![]() .
.
Evident cu cat ![]() este mai mare, aproximarea integralei
este mai mare, aproximarea integralei ![]() este mai buna. Un
astfel de calcul se poate efectua si tabelar ca mai jos.
este mai buna. Un
astfel de calcul se poate efectua si tabelar ca mai jos.

Metoda Simpson
In cadrul acestei metode se pastreaza
principiul de la metoda trapezelor, insa aproximarea functiei de
integrat pe portiuni nu se face prin segmente de dreapta, ci prin
arce de parabola de gradul doi; ![]() (Fig. 26).
(Fig. 26).

Cunoscand trei puncte consecutive prin
care trece parabola se pot determina coeficientii ![]() ca solutii ale sistemului
ca solutii ale sistemului
 (9.3)
(9.3)
Calculand acesti coeficienti si
efectuand apoi integrarea obtinem pentru aria ![]() valoarea:
valoarea:
![]()
Prin generalizare obtinem:
![]() (9.4)
(9.4)
sau:
![]() (9.5)
(9.5)
unde:
![]() ;
;
![]() ;
;
![]() .
.
O prima observatie care
rezulta este ca numarul de intervale in care se divizeaza
domeniul ![]() trebuie sa fie
par.
trebuie sa fie
par.
Calculul se poate realiza tabelar dupa cum urmeaza:
Tabelul 5
|
Nr. ordonata |
Ordonata |
Coeficient Simpson |
|
|
I |
II |
III |
IV |
|
|
|
||
|
|
|
||
|
|
|
||
|
| |||
|
|
|
|
|
|
|
|
|
|
|
a |
|||
![]()
Metoda Cebasev
Metoda Cebasev este foarte
cunoscuta in domeniul naval fiind o varianta a metodei Gauss si
care se bazeaza pe principiul intervalelor inegale dispuse in interiorul
unui interval centrat fata de origine ![]() .
.
Conform cu figura 27 , aria ![]() este egala cu
valoarea numerica a integralei
este egala cu
valoarea numerica a integralei ![]() .
.
Daca presupunem ca ![]() are forma matematica
a unui polinom de gradul
are forma matematica
a unui polinom de gradul ![]() :
:
![]() (9.7)
(9.7)
atunci
 (9.8)
(9.8)
unde
![]() sau
sau ![]() dupa cum
dupa cum ![]() este par sau impar.
este par sau impar.
Pe de alta parte, acceptam pentru integrala de mai sus forma:
![]() (9.9)
(9.9)
unde
![]() si sunt
necunoscutele problemei.
si sunt
necunoscutele problemei.

Dar
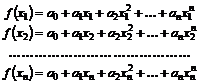 (9.10)
(9.10)
Daca introducem (9.10) in (9.9) obtinem:
![]() (9.11)
(9.11)
Comparand relatiile (9.8) si (9.11) se obtine sistemul:
 (9.12)
(9.12)
Din prima conditie rezulta:
![]() (9.13)
(9.13)
iar
![]() sunt solutiile
sistemului:
sunt solutiile
sistemului:
 (9.14)
(9.14)
Sa particularizam pentru
cazul ![]()
![]()
si
 (9.15)
(9.15)
Solutia acestui sistem este:
![]()
In consecinta
![]() (9.16)
(9.16)
Similar se pot dezvolta formule pentru orice numar de termeni, coeficientii fiind prezentati in tabelul de mai jos.
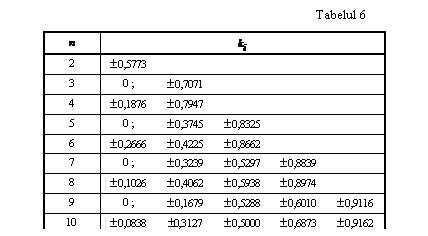
Aplicarea metodei Cebasev presupune parcurgerea urmatorului algoritm:
- Se adopta numarul ![]() in functie de
complexitatea curbei ;
in functie de
complexitatea curbei ;
- Se calculeaza abscisele ![]() cu relatia:
cu relatia:
![]() (9.17)
(9.17)
- Se extrag ![]() ;
;
- Se calculeaza valoarea integralei cu relatia:
![]() (9.18)
(9.18)
In cazul integrarii numerice se poate apela cu succes la mijloacele automate de calcul putandu-se folosi programe specializate existente in acest scop.
10. Calculul de carene inclinate
Formulele de calcul pentru elementele
hidrostatice ale carenei deduse anterior sunt valabile, asa cum am aratat
in ipoteza de - nava pe carena dreapta - ![]() . In procesul de exploatare a navei insa; in marea
majoritate a cazurilor, nava are o pozitie oarecare in raport cu suprafata
apei, inclinata atat transversal cat si longitudinal. In cele ce
urmeaza vom stabili relatii de calcul care sa permita
determinarea volumului carenei
. In procesul de exploatare a navei insa; in marea
majoritate a cazurilor, nava are o pozitie oarecare in raport cu suprafata
apei, inclinata atat transversal cat si longitudinal. In cele ce
urmeaza vom stabili relatii de calcul care sa permita
determinarea volumului carenei ![]() si a coordonatelor centrului de carena
si a coordonatelor centrului de carena ![]() pentru o pozitie
oarecare a navei.
pentru o pozitie
oarecare a navei.
10.1. Diagrama Bonjean
Sa consideram o sectiune transversala oarecare prin nava ca in Fig. 28, a.
Asa cum am aratat anterior aria imersa a acestei sectiuni se calculeaza cu formula (8.39).
![]()

Aria imersa a acestei sectiuni
transversale de la ![]() pana la o plutire
oarecare avand pescajul
pana la o plutire
oarecare avand pescajul ![]() se calculeaza cu
formula:
se calculeaza cu
formula:
![]() (10.1)
(10.1)
Variatia acestei arii in functie
de pescaj este prezentata in Fig. 28, b respectiv corespunzator unui
pescaj oarecare ![]() , se aseaza pe orizontala un segment
, se aseaza pe orizontala un segment ![]() egal cu valoarea lui
egal cu valoarea lui ![]() la o scara de
reprezentare convenabil aleasa. In felul acesta se poate calcula pentru
orice plutire
la o scara de
reprezentare convenabil aleasa. In felul acesta se poate calcula pentru
orice plutire ![]() , aria sectiunii transversale imerse. Deoarece in multe
probleme din teoria navei intereseaza intreaga arie a sectiunii
transversale (de exemplu: calculul volumului etans al corpului navei) ,
este necesar sa se calculeze si sa se introduca in grafic si
aria marginita de curbura transversala a puntii, adica
portiunea
, aria sectiunii transversale imerse. Deoarece in multe
probleme din teoria navei intereseaza intreaga arie a sectiunii
transversale (de exemplu: calculul volumului etans al corpului navei) ,
este necesar sa se calculeze si sa se introduca in grafic si
aria marginita de curbura transversala a puntii, adica
portiunea ![]() . In cele mai multe cazuri selatura puntii in sens transversal
este parabolica cu sageata
. In cele mai multe cazuri selatura puntii in sens transversal
este parabolica cu sageata ![]() . Aria corespunzatoare acestei selaturi care va trebui
adaugata este
. Aria corespunzatoare acestei selaturi care va trebui
adaugata este ![]() . Vom mai observa ca
. Vom mai observa ca ![]() este punct de inflexiune pentru curba
este punct de inflexiune pentru curba ![]() , iar tangenta in punctul
, iar tangenta in punctul ![]() este paralela cu
axa
este paralela cu
axa ![]() .
.
La navele construite din lemn , dimensiunile de calcul ale sectiunii transversale se considera la exteriorul bordajului, in timp ce la navele metalice aceleasi dimensiuni se masoara la interiorul bordajului.
Reprezentarea grafica asamblata a variatiei ariilor sectiunilor transversale, pentru toate cuplele navei, poarta denumirea de diagrama Bonjean, de la numele inginerului francez care a propus aceasta reprezentare.
Intr-o prima varianta, pentru
trasarea diagramei Bonjean se traseaza conturul corpului navei in ![]() precum si proiectia
pe acest plan a liniei puntii in bord, alegandu-se scari diferite de
reprezentare pentru lungimea navei si inaltimea ei,
realizandu-se astfel o 'contractie' a navei pe lungime (Fig.
29).
precum si proiectia
pe acest plan a liniei puntii in bord, alegandu-se scari diferite de
reprezentare pentru lungimea navei si inaltimea ei,
realizandu-se astfel o 'contractie' a navei pe lungime (Fig.
29).

Pe
acest contur se mai traseaza cuplele pentru care s-au efectuat calculele
ariilor precum si liniile suprastructurilor cum sunt duneta si teuga.
Se completeaza desenul cu trasarea curbelor ![]() , precum si cu scarile de reprezentare.
, precum si cu scarile de reprezentare.
Diagrama Bonjean poate fi reprezentata
si intr-o alta forma (Fig. 30), inlocuind reprezentarea ![]() corespunzatoare
fiecarei cuple cu o scala pe care sunt reprezentate numeric ariile
imerse.
corespunzatoare
fiecarei cuple cu o scala pe care sunt reprezentate numeric ariile
imerse.

In prima varianta, pentru o
plutire oarecare ![]() a gasi aria imersa
a cuplei 3 inseamna a inmulti segmentul
a gasi aria imersa
a cuplei 3 inseamna a inmulti segmentul ![]() cu scara ariilor. In a
doua varianta este mult mai usor sa citim pe scala ariilor la
intersectia dintre
cu scara ariilor. In a
doua varianta este mult mai usor sa citim pe scala ariilor la
intersectia dintre ![]() si cupla 3.
si cupla 3.
Exista si o a treia
modalitate de reprezentare a diagramei Bonjean (Fig. 31) trasand curbele ![]() raportate la aceeasi
axa verticala, cele din jumatatea prova fiind in dreapta axei
iar cele din jumatatea pupa in stanga axei, conform conventiei. O
astfel de reprezentare prezinta avantajul ca ocupa mai putin
spatiu dar prezinta dezavantajul necunoasterii pescajului
corespunzator cuplei pentru o plutire oarecare. Acesta se va calcula cu
formula
raportate la aceeasi
axa verticala, cele din jumatatea prova fiind in dreapta axei
iar cele din jumatatea pupa in stanga axei, conform conventiei. O
astfel de reprezentare prezinta avantajul ca ocupa mai putin
spatiu dar prezinta dezavantajul necunoasterii pescajului
corespunzator cuplei pentru o plutire oarecare. Acesta se va calcula cu
formula
![]() (10.2)
(10.2)
unde
![]() este pescajul mediu al
navei sau pescajul la cuplul maestru.
este pescajul mediu al
navei sau pescajul la cuplul maestru.
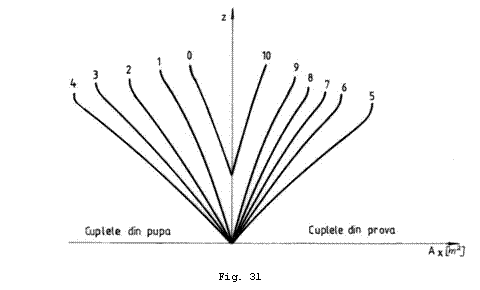
Diagrama Bonjean se foloseste pentru rezolvarea unor probleme importante de teoria navei. Astfel cu ajutorul diagramei Bonjean este usor de calculat volumul carenei si coordonatele centrului de carena pentru o plutire oarecare inclinata in plan longitudinal.
Cunoscute fiind formulele:
 si
si 
si
din diagrama Bonjean valorile ariilor imerse ale cuplelor ![]() ; apoi aplicand o procedura de integrare numerica,
problema este rezolvata. Din considerente de simetrie, cand nava nu este
inclinata transversal
; apoi aplicand o procedura de integrare numerica,
problema este rezolvata. Din considerente de simetrie, cand nava nu este
inclinata transversal ![]() , centrul de carena se gaseste in
, centrul de carena se gaseste in ![]() deci
deci ![]() , iar cota centrului de carena fata de linia
plutirii se calculeaza cu relatia:
, iar cota centrului de carena fata de linia
plutirii se calculeaza cu relatia:
 (10.3)
(10.3)
Cunoscand ![]() si
si ![]() se poate pozitiona
exact centrul de carena
se poate pozitiona
exact centrul de carena ![]() cunoscand si pozitia
plutirii inclinata longitudinal
cunoscand si pozitia
plutirii inclinata longitudinal ![]() dupa urmatorul
algoritm (Fig.32).
dupa urmatorul
algoritm (Fig.32).
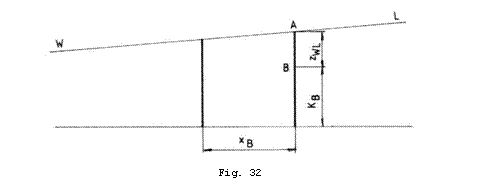
- se masoara ![]() de la cuplul maestru
de la cuplul maestru ![]() ;
;
- se determina punctul ![]() la intersectia
verticalei dusa la
la intersectia
verticalei dusa la ![]() cu plutirea inclinata
cu plutirea inclinata
![]() ;
;
- se masoara de la punctul ![]() in jos pe verticala,
valoarea
in jos pe verticala,
valoarea ![]() si se gaseste
pozitia lui
si se gaseste
pozitia lui ![]() .
.
10.2. Diagrama de asieta
Daca in diagrama
Bonjean se construiesc o serie de plutiri; calculandu-se pentru fiecare volumul
de carena corespunzator ![]() si abscisa
centrului de carena
si abscisa
centrului de carena ![]() se poate construi
diagrama de asieta, foarte utila din punct de vedere practic. Un
model de diagrama de asieta este prezentata in Fig. 33.
se poate construi
diagrama de asieta, foarte utila din punct de vedere practic. Un
model de diagrama de asieta este prezentata in Fig. 33.

In 'diagrama de
asieta' sunt prezentate curbele ![]() si
si ![]() Intrandu-se cu
pescajele
Intrandu-se cu
pescajele ![]() si
si ![]() masurate la scarile
de pescaj, se determina pozitia punctului
masurate la scarile
de pescaj, se determina pozitia punctului ![]() de pe diagrama si
prin interpolare vom obtine volumul carenei
de pe diagrama si
prin interpolare vom obtine volumul carenei ![]() si abscisa
centrului de carena
si abscisa
centrului de carena ![]() corespunzatoare
acestei situatii de plutire. Asadar 'diagrama de asieta'
permite determinarea marimilor
corespunzatoare
acestei situatii de plutire. Asadar 'diagrama de asieta'
permite determinarea marimilor ![]() si
si ![]() oricare ar fi pescajele
oricare ar fi pescajele ![]() si
si ![]() cunoscute.
cunoscute.
10.3. Calculul volumului carenei si a coordonatelor centrului de carena pentru o plutire
oarecare. Curbele integrale ale sectiunilor transversale.
Asa cum am aratat in 5, o
plutire oarecare a unei nave este definita de urmatorii trei
parametrii: pescajul mediu ![]() , inclinarea longitudinala
, inclinarea longitudinala ![]() si inclinarea
transversala
si inclinarea
transversala ![]() .
.
Pentru o sectiune transversala
oarecare din nava, pescajul in ![]() se poate calcula cu
formula:
se poate calcula cu
formula:
![]() (10.4)
(10.4)
unde
![]() este distanta de
la sectiunea transversala la planul sectiunii de la mijlocul
navei. Reamintim ca
este distanta de
la sectiunea transversala la planul sectiunii de la mijlocul
navei. Reamintim ca ![]() atunci cand sectiunea se gaseste in prova si
atunci cand sectiunea se gaseste in prova si
![]() cand nava este aprovata.
Deasemenea urma plutirii pe aceasta sectiune va face unghiul
cand nava este aprovata.
Deasemenea urma plutirii pe aceasta sectiune va face unghiul ![]() cu
cu ![]()
Sa consideram pentru inceput o sectiune transversala oarecare ca in Fig. 34.

Sectiunea
fiind simetrica fata de axa ![]() vom nota cu
vom nota cu ![]() - aria jumatatii de sectiune, cu
- aria jumatatii de sectiune, cu ![]() - momentul static al aceleiasi suprafete in raport
cu axa
- momentul static al aceleiasi suprafete in raport
cu axa ![]() , respectiv cu
, respectiv cu ![]() - momentul static in raport cu axa
- momentul static in raport cu axa ![]() . Formulele de calcul pentru aceste marimi sunt:
. Formulele de calcul pentru aceste marimi sunt:
![]() (10.5)
(10.5)
![]() (10.6)
(10.6)
![]() (10.7)
(10.7)
Reprezentarea grafica a variatiilor
![]() ;
; ![]() si
si ![]() poarta numele de
'curbele integrale ale sectiunii transversale'. Valorile acestor
marimi pentru o plutire dreapta de pescaj
poarta numele de
'curbele integrale ale sectiunii transversale'. Valorile acestor
marimi pentru o plutire dreapta de pescaj ![]() sunt prezentate in
Fig. 34, b.
sunt prezentate in
Fig. 34, b.
Sa consideram in continuare o
sectiune transversala situata la abscisa ![]() si corespunzator
'curbele integrale' (Fig. 35) si o plutire
si corespunzator
'curbele integrale' (Fig. 35) si o plutire ![]() inclinata in sens
transversal. Ne propunem sa gasim o modalitate de calcul a acelorasi
marimi pentru portiunea imersa corespunzatoare acestei sectiuni
transversale.
inclinata in sens
transversal. Ne propunem sa gasim o modalitate de calcul a acelorasi
marimi pentru portiunea imersa corespunzatoare acestei sectiuni
transversale.

Plutirea
inclinata intersecteaza ![]() in
in ![]() si conturul sectiunii
transversale in punctele
si conturul sectiunii
transversale in punctele ![]() si
si ![]() ; echivalente unor plutiri drepte si pentru care se
citesc din curbele integrale valorile:
; echivalente unor plutiri drepte si pentru care se
citesc din curbele integrale valorile: ![]() .
.
Aria imersa ![]() a sectiunii
transversale se poate scrie :
a sectiunii
transversale se poate scrie :
![]()
Momentul static al suprafetei ![]() in raport cu axele
in raport cu axele ![]() si
si ![]() se exprima ca suma
algebrica a momentelor suprafetelor ce o compun (pentru momentul in
raport cu axa
se exprima ca suma
algebrica a momentelor suprafetelor ce o compun (pentru momentul in
raport cu axa ![]() se va observa ca
suprafetele din dreapta axei au momentul pozitiv si cele din stanga
negativ).
se va observa ca
suprafetele din dreapta axei au momentul pozitiv si cele din stanga
negativ).
Componentele ariei si ale
momentelor statice in raport cu axele ![]() si
si ![]() se calculeaza cu
formulele :
se calculeaza cu
formulele :
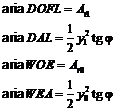
Pentru momentele statice in raport cu
axa ![]() :
:

|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2764
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved