| CATEGORII DOCUMENTE |
| Agricultura | Asigurari | Comert | Confectii | Contabilitate | Contracte | Economie |
| Transporturi | Turism | Zootehnie |
| Navigatie |
Pentru fiecare mod de transport se pot distinge, in mod conventional doua componente (sectoare): pe de o parte infrastructura si serviciile de gestiune, intretinere si exploatare aferente, iar pe de alta parte prestarile de servicii folosind autovehicule, material rulant, nave sau aeronave. Din punct de vedere al structurii productive, aceste doua sectoare prezinta caracteristici tehnice si economice foarte diferite.
Infrastructurile de transport comporta indivizibilitati pronuntate care se traduc prin existenta unor costuri fixe importante. Lipsa de divizibilitate a sectorului implica faptul ca gestiunea nu poate fi realizata intr-un regim de libera concurenta a unitatilor de productie distincte, care se confrunta pe piata[43]. Statul trebuie sa intervina pentru a obtine o alocare optimala a resurselor. Din contra, presupunand ca infrastructurile exista, prestatiile de servicii constituie, in general, activitati divizibile.
Primii analisti ai productiei de transport si ai functiei costului de transport [44], , inca din deceniul 6 al secolului trecut, au demonstrat faptul ca masurarea agregata a productiei de transport prin tone.km sau calatori.km nu poate surprinde complexitatea serviciilor oferite de un operator oarecare de transport.
Astfel, de exemplu, atunci cand se inregistreaza o crestere a costurilor unui operator cu 4% intr-un interval de referinta cunoscut, in conditiile unei cresteri cu 5% a numarului de tone.km realizate, nu se poate preciza modul in care au fost generate aceste cresteri atat pentru costuri cat si pentru volumul prestatiei. Volumul traficului putea creste:
doar prin cresterea cantitatii transportate pe ruta obisnuita,
prin mentinerea cantitatii si transportarea ei pe o distanta mai mare, sau
prin transportarea unor cantitati mai mici pe mai multe rute.
Agregarea productiei, datorita utilizarii retelei conexe si conective, poate conduce fie la subestimarea, fie la supraestimarea randamentelor de scara a productiei (efectelor economice pentru productia pe scara larga) si, mai mult, poate chiar ascunde cauza acestor randamente.
Cei mai multi operatori de transport realizeaza servicii de transport de marfa pentru diferite tipuri de produse, cu diferite atribute ale serviciului, utilizand o retea, intre o multime de origini si destinatii.
Astfel, pentru o productie de transport
de tip i, ![]() , caracterizata prin vectorul atributelor ,
, caracterizata prin vectorul atributelor , ![]() , cand se utilizeaza m
factori de productie, fiecare cu pretul sau unitar, pj si se produc n tipuri de servicii, functia de cost a operatorului care
trebuie determinata este de forma:
, cand se utilizeaza m
factori de productie, fiecare cu pretul sau unitar, pj si se produc n tipuri de servicii, functia de cost a operatorului care
trebuie determinata este de forma:
![]() (1)
(1)
Forma estimata a unei astfel de functii de cost poate fi foarte complexa, datorita, mai ales interactiunii dintre diferitele atribute ale serviciilor oferite. O astfel de forma functionala este cunoscuta sub denumirea de functie de cost multi-produs. Este diferita de functia de cost simpla cu o singura variabila reprezentand o agregare a nivelurilor de productie - C(y).
Pentru simplificarea efortului necesar identificarii unei functii de cost complexa se adopta metode de agregare la diferite niveluri a unor variabile din rel. (1). Se obtine astfel o functie de cost hedonic[46].
Prin definitie, functia de cost hedonic reprezinta functia de cost, cu o singura masura agregata a productiei (celelalte variabile caracteristice tipurilor de servicii realizate fiind la randul lor agregate), echivalenta functiei de cost multi-produs, completa si cu variabile explicite, cum este cea din relatia (1).
Astfel, pentru estimarea unei functii de cost cu un mare numar de tipuri de productii oferite (cum este cazul deplasarilor intre o multime de origini si o multime de destinatii intr-o retea), se pot agrega productiile realizate intr-o singura variabila, de exemplu tone.km.; alaturi de aceasta variabila agregata se introduc variabilele hedonice cum sunt, de exemplu, lungimea medie de transport, cantitatea medie de transport, numarul mediu de calatori transportati in unitatea de timp de referinta, proportia marfurilor transportate ca unitati de incarcatura etc.
Se poate constitui o functie de
productie hedonica ![]() , cu ajutorul careia se identifica functia de
cost hedonic, care este de forma:
, cu ajutorul careia se identifica functia de
cost hedonic, care este de forma:
![]() (2)
(2)
Din punctul de vedere al estimarii, aceasta functie impune indeplinirea unor conditii:
functia hedonica de productie ![]() nu trebuie sa
aiba variabile yi
si qi care sa
fie dependente de preturile factorilor de productie, pj,
nu trebuie sa
aiba variabile yi
si qi care sa
fie dependente de preturile factorilor de productie, pj,
trebuie sa contina masuratori care sa tina cont de efectele pe care le are utilizarea retelei asupra costului.
Cea mai utilizata forma pentru functia de productie de bunuri materiale dar si pentru productie de servicii este cea de tip Cobb-Douglas. Ea este folosita si in studiile descriptive (statistice) din domeniul transporturilor , cu restrictii dificil de neglijat.
Forma uzuala a functiei de productie de transport Cobb-Douglas este:
![]() (3)
(3)
unde:
y reprezinta nivelul serviciului produs,
K capitalul fix implicat,
L - forta de munca,
F - consum de energie (combustibili),
A, a, b, e - constante de calibrare a modelului.
Daca salariul mediu pe unitatea de timp de referinta a analizei este pL, costurile unitare ale capitalului investit sunt pK, iar pretul unitar al energiei consumate - pF,, cheltuielile totale pentru producerea serviciului de transport sunt:
![]() (4)
(4)
Functia obiectiv a operatorului de transport (gestionar al unui parc de vehicule sau administratorul infrastructurii de transport) este aceea de a realiza fiecare unitate de productie cu cele mai reduse costuri.
Problema de optimizat este atunci:
![]() min
min
cu restrictia:
![]()
Rezolvarea consta in constituirea
functiei Lagrange L![]() si determinarea punctelor ei de extrem. Astfel, pentru:
si determinarea punctelor ei de extrem. Astfel, pentru:
![]() (5)
(5)
se scriu conditiile de optim:
![]() (6.a)
(6.a)
![]() (6.b)
(6.b)
![]() (6.c)
(6.c)
![]() (6.e)
(6.e)
Nivelul de productie cel mai ridicat[48], obtinut cu cele mai scazute costuri este realizat pentru combinatia de consum de resurse K, L, F, care indeplineste proprietatea:
![]() (7)
(7)
Consumurile de resurse K, L, F din relatiile (6) care indeplinesc proprietatea (7), conduc la functia de productie de forma:
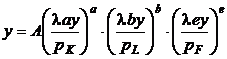 , sau
, sau
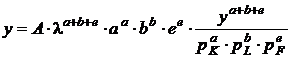 (8)
(8)
Parametrul ![]() - costul marginal
pentru realizarea unei unitati suplimentare de productie, se
determina atunci:
- costul marginal
pentru realizarea unei unitati suplimentare de productie, se
determina atunci:
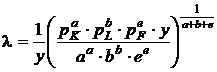 (9)
(9)
Cu ajutorul relatiei (9) se obtin resursele K, L, F si functia costului de productie simpla:
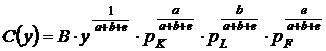 (10)
(10)
unde:
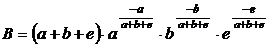 .
.
Pentru o forma mai simpla a functiei de cost se poate logaritma intreaga relatie (10):
![]() (11)
(11)
unde: ![]() ;
; ![]() ;
; ![]()
![]()
![]()
Corespunzator functiei de cost din relatia (10), de cate ori va creste salariul unitar, de exemplu cu 1%, costul total va creste cu r3 procente.
In plus, intr-o functie de cost cu structura Cobb-Douglas, proportia cheltuielilor pentru fiecare factor de productie este o constanta, dependenta de preturile factorilor de productie si de nivelul productiei, y. Astfel, proportia in costul total, cheltuita pentru forta de munca va fi intotdeauna r3 si tot astfel, proportia in costul total reprezentata de capitalul fix sau de consumul de energie (combustibili) va fi intotdeauna r2 si, respectiv r4.
Din ecuatia (4)
si lema lui Shepard 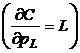 (Anexa I),
rezulta ca:
(Anexa I),
rezulta ca:
![]() ;
;
adica, r3 este "factorul muncii", proportia din costul total alocata fortei de munca.
Deoarece, suma proportiilor factorilor de productie trebuie sa fie egala cu unitatea, functia de cost Cobb-Douglas este adecvata analizei, doar daca:
r2 + r3 + r4 = 1.
Se cunoaste de asemenea ca, o functie de cost cu structura Cobb-Douglas are elasticitatea substituirii unui factor de productie cu un altul intotdeauna egala cu unitatea.
Pentru functia
de productie de forma ![]() , continua si derivabila, definita pe
multimea numerelor reale pozitive, cu valori in acelasi domeniu, rata
marginala de substituire a primului factor cu cantitati din al
doilea factor pentru a mentine acelasi nivel de productie, y este:
, continua si derivabila, definita pe
multimea numerelor reale pozitive, cu valori in acelasi domeniu, rata
marginala de substituire a primului factor cu cantitati din al
doilea factor pentru a mentine acelasi nivel de productie, y este:
![]() ,
,
iar elasticitatea substituirii factorului 1 cu 2:
![]()
Conditiile pe care trebuie sa le indeplineasca productia din transporturi (oricare ar fi sectorul sau modul analizat), pentru a putea fi modelata prin intermediul unei structuri Cobb-Douglas, sunt mult prea restrictive.
Una din cele mai importante etape in studiul functiei de cost din transporturi a fost aceea a utilizarii unei forme functionale mult mai putin restrictive, adecvata analizelor descriptive. Acesta este cunoscuta sub denumirea de forma flexibila si provine fie dintr-o structura de productie generalizata Leontief [50], fie dintr-o functie translog .
O functie de cost de productie pe termen lung, cu structura translog, pentru n tipuri de servicii realizate, de dimensiuni yi, cand sunt folositi m factori de productie, la preturile pj, are forma:
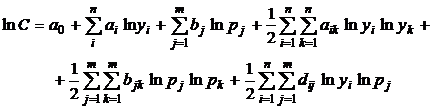 (12)
(12)
Pentru ca functia de acesta forma sa fie omogena de gradul intai in raport cu preturile, trebuie indeplinite conditiile:
![]() ,
,
![]()
![]()
In plus coeficientii trebuie sa fie simetrici astfel incat sa aiba o forma simpla a derivatei de ordinul 2.
Atunci cand in datele experimentale se inregistreaza si valori nule, utilizarea unei forme translog pentru functia de cost devine problematica datorita valorii infinite pentru logaritmul unei valori nule.
Utilizarea unei astfel de functii de cost prezinta avantajul urmator: de cele mai multe ori, din practica uzuala, se dispune de date legate de valoarea alocata din costul total pentru fiecare factor de productie, iar acest fapt intrebuintat adecvat, poate imbunatati precizia estimarii functiei de cost total.
Astfel, pentru factorul al carui pret este pi, se poate formula ecuatia care identifica proportia de cheltuieli alocata acestui factor, din costul total:
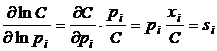 (13
)
(13
)
unde si reprezinta proportia din costul total cheltuita pe factorul i, in cantitatea xi.
Ecuatia proportiei factorului i este:
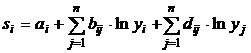 (14).
(14).
Functia de cost Cobb-Douglas este un caz special al functiei translog din relatia (12). Daca toti termenii care contin aij, bij si dij sunt egali cu 0, functia ramasa este chiar:
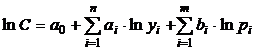
care reprezinta o functie de cost Cobb-Douglas pentru n tipuri de servicii produse, fiind necesari m factori de productie.
Termenii suplimentari de ordinul doi in functia translog permit ca elasticitatile costului in functie de productie si in functie de preturile tuturor factorilor de productie sa varieze (in loc sa ramana constante, asa cum se observa la o functie de cost cu structura Cobb-Douglas) corespunzator productiei sau preturilor.
De exemplu, se pot realiza astfel estimari ale randamentelor de scara in functie de dimensiunea prestatiei efectuate. Acesta este si sensul in care functia translog este numita "flexibila"[52].
Esantionul de date poate include valoarea 0 pentru unele observatii. Asa este cazul, de exemplu, al anumitor sectii de circulatie de cale ferata care au valori pozitive ala traficului de marfa si calatori, in timp ce altele sunt specializate doar pentru traficul de marfa (cu trafic de calatori nul). In acest caz specificarea functiei translog este problematica, deoarece logaritmul din valoarea 0 este egal cu -
Rezolvarea problemei a condus la dezvoltarea asa-numitei "transformate Box - Cox" .
Daca datele referitoare la y sunt uneori nule, atunci in loc de a introduce datele ca log yi, cu transformata Box-Cox, aceste date sunt introduse ca:
![]() (15)
(15)
unde l este un parametru care se poate determina cu ajutorul regresiei liniare. In acest caz, numarul de parametri pentru a fi estimati este acelasi ca si in cazul functiei de cost translog standard, cu exceptia celui suplimentar, l
Exista doua valori semnificative pentru l
Astfel, daca l = 1, atunci 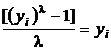 , ceea ce inseamna ca transformata Box-Cox a lui yi este chiar yi.
, ceea ce inseamna ca transformata Box-Cox a lui yi este chiar yi.
Daca l = 0, se poate demonstra ca:
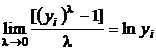
Prin intermediul transformatei Box-Cox se pot reprezenta cazurile speciale ale nivelului productiei yi, cand acesta evolueaza liniar (l = 1) sau logaritmic (l = 0), insa nu se poate preciza nimic despre toate celelalte valori ale lui yi.
Asa cum s-a evidentiat si mai inainte, una din caracteristicile productiei de servicii de transport care se impune a fi studiata este aceea a existentei randamentelor de scara.
Productia poate creste:
fie printr-un volum de transport mai mare transportat pe o retea fixata, crescand astfel densitatea traficului,
fie prin dezvoltarea retelei chiar daca densitatea traficului de-a lungul arcelor ramane constanta.
Distinctia esentiala dintre randamentul de scara si cel de densitate a serviciului este ilustrata in figura 1 .
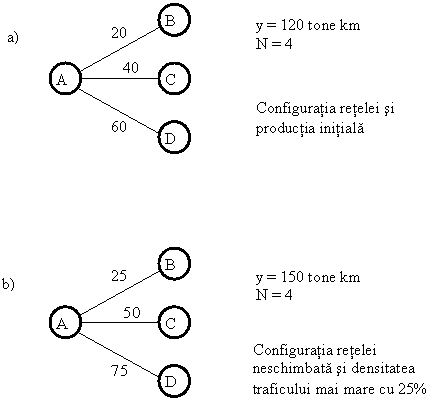
Fig. 1. Randamentul de scara si de densitate pentru serviciile oferite intr-o retea de transport
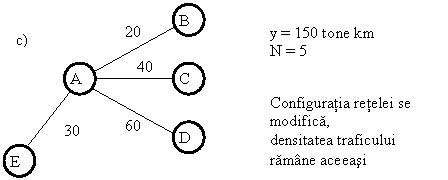
Fig. 1. Randamentul de scara si de densitate pentru serviciile oferite pe o retea de transport (continuare)
Se considera configuratia retelei in situatia initiala din figura 1.a. Operatorul de transport deserveste patru noduri (localizari amplasate in noduri diferite legate prin retea) (A, B, C si D), N = 4. Dimensiunea traficului (masurata in tone km, de exemplu) pe fiecare legatura este indicata pe figura, iar totalul activitatii desfasurate la nivelul retelei este y = 120 tone km.
Se presupune o crestere a traficului cu 25%, asa incat y = 150 tone km la nivelul intregii retele. Aceasta sarcina poate fi realizata in mai multe feluri.
Se poate studia cazul distribuirii cresterii la nivelul fiecarui arc, reteaua ramanand neschimbata, asa cum se poate observa in figura 1.b.
O alta modalitate de crestere a productiei de transport este cea ilustrata in figura 1.c. Reteaua de transport deservita se extinde prin utilizarea unei noi legaturi care preia intreaga crestere a traficului, densitatea ramanand neschimbata.
Pentru o functie de cost pe termen lung, in care costul total C depinde de tipurile de productie realizate, y1, y2, ., yn si de numarul de noduri deservite de retea, N se poate defini -randamentul de densitate RD prin :
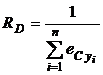 (16)
(16)
unde ![]() reprezinta
elasticitatea costului total in functie de nivelul productiei de tip i, definita tipic astfel:
reprezinta
elasticitatea costului total in functie de nivelul productiei de tip i, definita tipic astfel:
![]() (17).
(17).
Randamentul de densitate este, prin urmare, o masura a efectelor economice de productie pe scara mare cand volumul de trafic creste, insa numarul de zone deservite prin retea este mentinut constant.
Economiile de densitate, randamentul constant sau diseconomii de densitate apar atunci cand RD este supra unitar, egal cu unitatea sau, respectiv, subunitar.
Randamentul de scara (fig. 1.c) este definit prin:
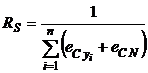 (18)
(18)
unde fata de
termenii utilizati in relatia 16 apare ![]() care reprezinta
elasticitatea costului total in functie de numarul de
localizarile clientilor deserviti.
care reprezinta
elasticitatea costului total in functie de numarul de
localizarile clientilor deserviti.
RS este o masura a economiilor de scara (dimensiune) atunci cand productia si dimensiunea retelei deservite se modifica. Apar efecte economice de scara daca RS > 1, dizeconomii de scara cand RD < 1 si efecte nule sau randamente constante cand RS = 1.
Atat operatorii cat si decidentii politici sunt interesati de dimensiunea randamentelor de densitate si de scara. Studiile asupra efectelor economice ale cresterii productiei[55], demonstreaza ca nu exista importante randamente de scara pentru transportul pe calea ferata, rutier sau aerian, in schimb, de cele mai multe ori, s-au obtinut importante randamente de densitate.
Decidentii politici sunt deseori interesati de masura in care economiile de densitate pot afecta competitia intre modurile de transport.
De exemplu, pentru un operator de cale ferata cu un randament de densitate semnificativ, posibilitatea de a creste pretul va fi limitata daca pe acea zona se va confrunta cu operatori rutieri si/sau fluviali si/sau cu transportul prin conducte.
Economiile de densitate sunt importante si in negocierile pentru fuziunea dintre operatori de transport. De cele mai multe ori fuziunea se realizeaza cu intentia de a obtine, in urma reorganizarii, costuri de productie unitare mai scazute, ceea ce nu se realizeaza intotdeauna cu usurinta.
In afara de studiul costurilor si a randamentelor de scara si de densitate (necesare in luarea deciziilor), pentru o cunoastere profunda a ofertei de servicii de transport este necesara analiza modului in care combinarea mai multor tipuri de productii poate afecta costul total.
Intr-un regim concurential dereglementat (liber), operatorii de transport pot oferi mai multe servicii. Apare atunci intrebarea daca un operator ar trebui sa-si diversifice serviciile sau, din contra, sa specializeze cat mai mult oferta sa. Pentru astfel de decizii, operatorul trebuie sa cunoasca modul in care costul total este influentat de numarul de tipuri de servicii realizate si de combinatia dintre ele.
Se considera, de exemplu, un operator de transport feroviar, care ofera doua tipuri de servicii, transport de calatori, de dimensiune y1 si transport de marfa, de dimensiune y2. Functia costului total de productie este C(y1, y2). Se poate pune intrebarea asupra modului in care o crestere a nivelului serviciului y1 va afecta costul marginal in raport cu nivelul productiei serviciului al doilea.
Matematic, costul
marginal in raport cu serviciul 1 este derivata partiala ![]() . Pentru a determina modul in care o crestere a lui y2 afecteaza costul
marginal in raport cu nivelul
productiei serviciului y1, se va calcula derivata
costului marginal
. Pentru a determina modul in care o crestere a lui y2 afecteaza costul
marginal in raport cu nivelul
productiei serviciului y1, se va calcula derivata
costului marginal ![]() in functie de
nivelul productiei y2,
adica
in functie de
nivelul productiei y2,
adica 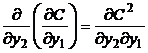 .
.
In ipoteza in care
nivelul costului marginal in raport cu serviciul y1
scade daca productia y2 creste, atunci 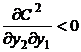 . Cel putin pentru o multime de observatii in
vecinatatea nivelului de servicii care intereseaza in analiza,
aceasta conditie demonstreaza existenta unei legaturi
intre costurile celor doua servicii oferite. Conditia
. Cel putin pentru o multime de observatii in
vecinatatea nivelului de servicii care intereseaza in analiza,
aceasta conditie demonstreaza existenta unei legaturi
intre costurile celor doua servicii oferite. Conditia 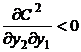 este denumita
conditie de existenta a complementaritatii
de cost intre serviciul 1 si 2.
este denumita
conditie de existenta a complementaritatii
de cost intre serviciul 1 si 2.
Daca, in
schimb, poate fi demonstrata conditia 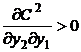 , atunci se spune ca cele doua servicii
prezinta proprietatea de non-complementare de cost; cel putin
pentru multimea de inregistrari din vecinatatea nivelului de
servicii analizat, atunci cand nivelul unui serviciu creste costul
marginal in raport cu celalalt serviciu creste.
, atunci se spune ca cele doua servicii
prezinta proprietatea de non-complementare de cost; cel putin
pentru multimea de inregistrari din vecinatatea nivelului de
servicii analizat, atunci cand nivelul unui serviciu creste costul
marginal in raport cu celalalt serviciu creste.
Complementaritatea si non-complementaritatea sunt notiuni "locale" datorita faptului ca descriu modul in care functia de cost se comporta in vecinatatea unei multimi de inregistrari. In acelasi timp insa, prezinta importanta si modul in care se pot produce la un cost mai scazut ambele tipuri de servicii de catre un acelasi operator.
In acest caz se determina daca exista economii sau dizeconomii (efecte pozitive sau negative) ale scopului propus care mai sunt numite si efecte economice ale specializarii serviciului.
Prin definitie un operator produce nivelul de servicii (y1, y2), in conditii de efecte economice (pozitive) ale acestui scop combinat, daca:
![]() (19)
(19)
adica producerea ambelor servicii este mai putin costisitoare decat in cazul in care cele doua servicii ar fi realizate de doi producatori in mod separat.
Atunci cand relatia (19) prezinta inegalitatea de semn opus, se spune ca exista dizeconomii de scop, caz in care apare ca mai avantajoasa productia specializata a fiecaruia dintre servicii de catre un singur operator (unul produce doar y1, iar celalalt doar y2).
Deoarece examinarea economiilor de scop necesita informatii asupra naturii si dimensiunii costurilor pentru toata plaja de niveluri ale serviciilor produse atunci cand serviciul al doilea este 0, este evident faptul ca functia de cost trebuie sa fie adecvata (adica sa poata surprinde valori ale costului total la niveluri de servicii nule).
O functie de cost de tip translog nu poate analiza economia de scop insa poate sluji la analiza complementaritatii sau non-complementaritatii costurilor.
Pentru descrierea economiilor de scop poate fi utilizata o functie translog generalizata (adica, o functie translog cu o transformare Box-Cox a productiei) sau alte forme funtionale cu elasticitate constanta a substitutiei intre variabile.
Studiile asupra economiilor de scop [57] din transporturi au relevat ca:
nu exista complementaritate de cost sau non-complementaritate in transportul de marfuri si calatori, pe calea ferata;
pot exista economii de specializare a celor doua tipuri de servicii pe calea ferata. Cu alte cuvinte, se pot inregistra reduceri ale costurilor totale rezultate din separarea operarii pe calea ferata a serviciilor de marfa de cele de calatori;
se manifesta dizeconomii de scop in cazul operarii comune a productiei de transport de marfa cu vehicule rutiere de mare capacitate alaturi de cele usoare;
in transportul aerian se manifesta, in mica masura o complementaritate de cost pentru transportul planificat (cu orar) si cel charter, in timp ce pentru transportul de calatori si cel de marfa s-au determinat non-complementaritati de cost;
In teoria economica analiza pe termen lung se refera la o perioada suficient de lunga, astfel incat toti factorii de productie pot fi modificati pentru a obtine nivelurile lor optime (din punctul de vedere al minimizarii costurilor) tinand cont de diferitele dimensiuni ale productiei realizate si vandute.
Functia de cost total a producatorului depinde de nivelul productiei realizate si de toate preturile si cantitatile factorilor de productie implicati.
In productia de transport, unde ponderea capitalului fix este mare, deciziile pe termen lung sunt ajustate cu ajutorul deciziilor pe termen scurt, cum este durata unui an sau semestru, cand nivelurile de productie si tarifarea se bazeaza pe costurile pe termen lung.
Pe termen scurt costurile totale pot fi clasificate in fixe si variabile. Cele fixe sunt asociate factorilor de productie care nu se modifica in perioada de analiza data, iar cele variabile sunt asociate factorilor care se pot modifica in functie de productia realizata.
Pe termen scurt, prin urmare, nu productia minimizeaza costurile sale variabile in functie de diferitele niveluri observate ale productiei.
Fie un producator de servicii de transport care este caracterizat de un nivel K al capitalului fix (dimensiunea firmei) si de L - nivelul fortei de munca si F - nivelul energiei consumate (factori variabili de productie). Functia costurilor variabile depinde de dimensiunea productiei realizate, de nivelul capitalului fix, de preturile unitare ale factorilor variabili, pL si pF.
Fie aceasta functie de cost variabil de forma:
![]() (20).
(20).
Functia costului total are atunci forma:
![]() (21)
(21)
unde r reprezinta pretul unitar al
capitalului fix iar ![]() reprezinta
nivelurile celor n tipuri de productii realizate si
observate.
reprezinta
nivelurile celor n tipuri de productii realizate si
observate.
Apare, in acest fel, necesar studiul empiric al costurilor totale pe termen scurt, concentrat asupra functiei de cost variabil. In plus, se impune analiza efectelor economice de scara si de densitate a serviciului prin introducerea in functia de cost a dimensiunii retelei, cum este N - numarul de noduri, adica trebuie luata in considerare o functie de cost variabil de forma:
![]() (22).
(22).
Se poate demonstra ca, efectele economice de densitate, SD au valoarea:
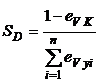 (23)
(23)
iar efectele economice de scara a serviciului, SS sunt:
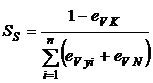 (24)
(24)
unde:
![]() reprezinta
elasticitatea costurilor variabile in raport cu capacitatea de productie
(sau alti factori de productie fixati pe termen scurt),
reprezinta
elasticitatea costurilor variabile in raport cu capacitatea de productie
(sau alti factori de productie fixati pe termen scurt),
![]() - elasticitatea
costului variabil in functie de nivelul productiei de categorie i,
- elasticitatea
costului variabil in functie de nivelul productiei de categorie i,
![]() - elasticitatea
costului variabil in functie de numarul de noduri deservite ale
retelei.
- elasticitatea
costului variabil in functie de numarul de noduri deservite ale
retelei.
Existenta efectelor economice ale specializarii serviciilor este limitata, insa acestea sunt crescatoare. Separarea serviciilor de transport pentru marfa de cele de calatori trebuie realizata in urma unor studii riguroase asupra complementaritatii costurilor si asupra efectelor economice ale scopului.
O dificultate pentru analist o constituie inregistrarea datelor de exploatare ale operatorului cu activitate integrata (de marfa si calatori) care, deseori, nu ofera evidente clare ale costurilor pentru diferite niveluri de servicii si pentru fiecare categorie, asa cum s-ar obtine din exploatarea separata a unei retele de cale ferata.
Pentru majoritatea transportatorilor rutieri se manifesta un randament de scara constant. Exista unele studii[58] care evidentiaza faptul ca in sectorul transportului de marfa, in unitati de incarcatura mai mica decat autocamioanele, se manifesta un randament de scara crescator, generat de efectele economice de densitate.
Cele mai multe studii ale transportului de marfuri in autovehicule comerciale usoare reflecta o structura tehnologica care conduce la o competivitate ridicata, in conditiile unei piete fara reglementari de pret si la intrarea pe piata a operatorilor.
Indata ce se incorporeaza in functia de cost si masuratorii de calitate a serviciului dar si constrangeri de pret, studiile indica doar un randament constant de scara.
Daca exista efecte de densitate, inseamna ca este dificila intrarea pe acea piata[59].
Aspectul functiei de cost din transporturi este influentat, de asemenea, de mediul de reglementari in care companiile evolueaza. O companie de transport se adapteaza reglementarilor; analistul insa trebuie sa identifice metode noi si imbunatatite de dezagregare a productiei realizate in raport cu variabilele asociate si de incorporare a atributelor serviciilor si a structurii retelei in functiile de cost.
Atat operatorii cat si decidentii politici trebuie sa inteleaga si sa cunoasca costurile fiecarei activitati de transport deoarece acestea reprezinta un element al evaluarii beneficiilor rezultate din operatiile intermodale si al accesului la retelele de transport. Prin cunoasterea functiilor de cost, pe de o parte, se pot identifica metode de crestere a productivitatii si se pot aduce modificarile tehnologice necesare, iar pe de alta, se pot evalua efectele reglementarilor adoptate.
Studiul functiilor de cost din transporturi este definitoriu in realizarea unui ansamblu eficient de decizii pentru a proiecta politici publice de succes.
Quinet, E. (1982) Infrastructures des transports. Bilans et perspectives. Chotard et Associes, Paris.
Mayer, J.R (1958) Some Methodological Aspects of Statistical Costing as Illustrated by the Determination of Rail Passenger Costs. American Economic Review, No.4, p.209-222.
Spady, R.H., Friedlaender, A.F. (1978) Hedonic Cost Function for the Regulated Trucking Industry. Bell Journal of Economics, No.9, p.154-179.
Jara-Diaz, S.R. (1982) The Estimation of Transport Cost Functions: A Methodological Review. Transportation Review, No.2, (vol.3), p.159-171.
Diewert, W.E., Wales, T.J. (1987) Flexible Functional Forms and Global Curvature Conditions. Econometrica, No.55, p.43-68.
Caves, D.W., Christensen, L.R., Tretheway, M.W. (1980) Flexible Cost Functions for Multiproduct Firms. Review of Economics and Statistics, No.62, p.477-481.
Diewert, W.E., Wales, T.J. (1987) Flexible Functional Forms and Global Curvature Conditions. Econometrica, 55(1), p.43-68.
Caves, D.W.,Christensen, L.R., Tretheway, M.W. (1980) Flexible functional Form for Multiproduct Firms. Rewiew of Economics and Statistics, 62, p.477-481.
Braeutgam, R.R, Daughety, A.F. (1983) On the Estimation of Return to Scale Using Variable Cost Function Economic Letters, 11 (1-2), p.25-31.
Savage, I. (1994) Scale Economies in Rail Transit Systems. Working Paper. Northwestern University, Deparment of Economics.
Friedlaender, Ann F. (1993) Rail Costs and Capital Adjustments in a Quasi-Regulated Environment. Journal of Transport Economics and Policy, 27 (2), p.131-152.
Braeutigam, R.R. (1999) Learning about cost. in Essays in Transportation Economics and Policy.A Handbook in Honor of John R. Meyer. (eds.Jos A. Gmez-Ibez, J.A,Tye, W.B., Winston, C.), Brookings Institution Press.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2965
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved