| CATEGORII DOCUMENTE |
| Agricultura | Asigurari | Comert | Confectii | Contabilitate | Contracte | Economie |
| Transporturi | Turism | Zootehnie |
| Navigatie |
1. PLANE SI LINII PRINCIPALE ALE OBSERVATORULUI PE SFERA TERESTRA
In navigatia maritima, siguranta navigatiei este obiectivul caruia se subordoneaza toate activitatile de la bordul navei. In acest context, orientarea pe mare devine un element foarte important.
In mare deschisa, orientarea nu ar fi posibila fara existenta unui sistem de referinta.
In fig.15 s-a considerat observatorul A plasat pe suprafata sferei terestre la o latitudine nordica oarecare.
Sunt reprezentate:
PnPs , axa polilor terestri;
QQ', ecuatorul terestru;
ZeNa, verticala punctului A considerat;
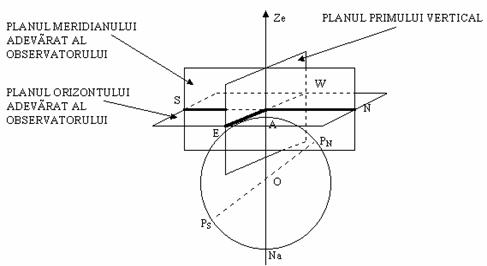
[ Fig.15 ] Plane si linii principale ale unui observator
Directia care uneste punctul observatorului cu centrul sferei terestre este verticala locului (AO); verticala locului este materializata de firul cu plumb, liber suspendat sub actiunea gravitatiei Pamantului.
Verticala locului prelungita la infinit inteapa sfera cereasca in doua puncte: zenitul (Ze), deasupra crestetului observatorului si nadirul (Na), in sens opus. De aceea, directia verticalei locului mai este denumita si linia zenit-nadir.
Planele care contin verticala locului se numesc plane verticale sau verticale. Verticalul care contine axa polilor terestri se numeste planul meridianului adevarat al observatorului(locului); intersectia acestui plan cu sfera terestra determina un cerc mare, denumit meridianul adevarat al observatorului (locului) sau meridianul observatorului (locului).
Planul verticalul perpendicular pe planul meridianului observatorului se numeste primul vertical. Orice plan perpendicular pe verticala locului se numeste orizont.
Planul orizontal care trece prin ochiul observatorului A se numeste orizont adevarat al observatorului.
Planul orizontal care trece prin centrul sferei terestre se numeste orizont astronomic (HH').
Dreapta de intersectie dintre planul meridianului observatorului cu planul orizontului adevarat al observatorului se numeste linia nord-sud (N-S). Sensul nordic al acestei linii este determinat de directia Polului Nord in raport cu pozitia observatorului.
Directia AN mai este denumita si directia nord adevarat, referindu-se la faptul ca este determinata de planul meridianului adevarat al observatorului; in acest caz, punctul cardinal nord este notat prin Na.
Dreapta de intersectie dintre planul orizontului adevarat al observatorului cu primul vertical se numeste linia est-vest (E-W). Sensurile estic si vestic ale acestei linii se stabilesc astfel: considerandu-ne in punctul A cu fata spre nord, sensul estic este spre dreapta, iar cel vestic spre stanga.
Liniile N-S si E-W se numesc linii sau directii cardinale.
Liniile cardinale sunt determinate in orice punct al sferei terestre, cu exceptia cazului cand observatorul se afla in unul din polii terestri. in acest caz verticala locului se confunda cu axa polilor terestri, astfel ca planul meridianului locului nu mai este un plan determinat. Planul meridianului locului fiind nedeterminat, inseamna ca nici liniile N-S si E-W nu mai pot fi stabilite in planul orizontului adevarat.
Liniile N-S si E-W impart orizontul adevarat al observatorului in patru cadrane. Denumirea fiecarui cadran are ca origine linia N-S si ca sens estul si vestul, deci:
cadranul I sau cadranul NE;
cadranul II sau cadranul SE;
cadranul III sau cadranul SW;
cadranul IV sau cadranul NW.
Liniile si planele definite mai sus sunt proprii pozitiei fiecarui observator pe sfera terestra.
2. DRUMURI SI RELEVMENTE
2.1. DRUM ADEVARAT
Orientarea pe mare presupune cunoasterea in permanenta a pozitiei navei si a directiei in care aceasta se deplaseaza; in acest context, se opereaza curent cu urmatoarele notiuni:
Directia Nord adevarat (Na) este semidreapta nordica a liniei NS, si este directia de referinta la care se raporteaza directia de deplasare a navei;
Reperele de navigatie sunt constructii special amenajate, cladiri importante usor de recunoscut de pe mare, forme de relief etc., trecute cu precizie in harta si consemnate in documentele nautice;
Directia de vizare la un reper este dreapta din
planul orizontului adevarat al observatorului, care uneste punctul
navei cu reperul.
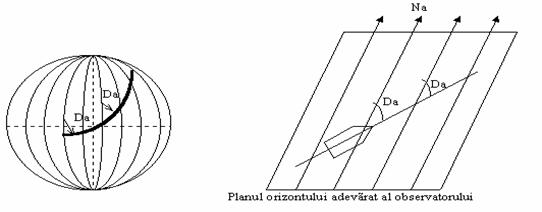
[ Fig.16] [Fig. 17 ]
Directia in care se deplaseaza nava se defineste cu ajutorul notiunii de drum adevarat (fig.16 si 17):
Da al navei este unghiul din planul orizontului adevarat masurat de la directia Na pana la axa longitudinala a navei, directia catre prova.
2.2. RELEVMENT ADEVARAT
Relevmentul adevarat (Ra) masurat la un reper F (Fig.18) se defineste ca fiind unghiul din planul orizontului adevarat al observatorului, masurat de la directia Na pana la directia de vizare la reper.
Relevmentul adevarat este un al doilea indicator important pentru orientarea pe mare; el raporteaza directia de vizare la un reper la directia Na.
2.3. RELEVMENT PROVA
Relevmentul prova (Rp) masurat la reperul F (vezi Fig.18) este unghiul din planul orizontului adevarat al observatorului, masurat de la directia prova a axei longitudinale a navei pana la directia de vizare la reper.
Relevmentul prova raporteaza directia de vizare la un reper la axa longitudinala a navei, directia catre prova; el constituie al treilea indicator important pentru orientarea pe mare.
Da, Ra si Rp se exprima in grade si zecimi de grad.
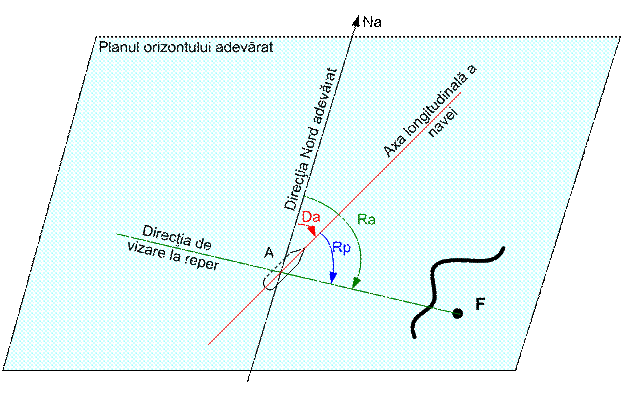 Fig.18 ] Drumuri si
relevmente
Fig.18 ] Drumuri si
relevmente
2.4. SISTEME DE MASURARE A DRUMURILOR SI RELEVMENTELOR IN PLANUL ORIZONTULUI ADEVARAT
Marimile unghiulare ale drumurilor si relevmentelor se exprima in grade sexagesimale. In trecut, in perioada velierelor, drumurile si relevmentele se exprimau in carturi.
In afara diferitelor unitati de masura in care se pot exprima drumurile si relevmentele, in navigatie se intalnesc mai multe sisteme de masurare a acestor unghiuri, privind originea lor de masurare.
In principiu, directiile/unghiurile masurate in planul orizontului adevarat al observatorului se raporteaza la directia Na. Prin exceptie, anumite unghiuri se pot masura fata de axa longitudinala a navei (cum este de exemplu relevmentul prova masurat la un reper).
Se definesc urmatoarele sisteme de masurare a unghiurilor in planul orizontului adevarat (POA) al observatorului:
1) Sistemul circular este sistemul care se utilizeaza in prezent, pe scara larga, in navigatia moderna. Toate celelalte sisteme de contare se folosesc restrictiv.
In sistem circular, unghiurile se masoara de la directia de referinta (Na sau prova), doar in sens retrograd, si iau valori de la 000 la 360
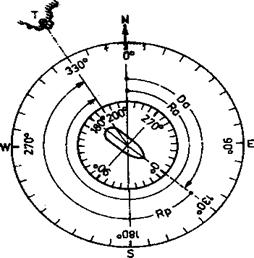
[ Fig 19 ] Sistemul circular de masurare a drumurilor si relevmentelor
Exemplu Da = 130.0 ;
Ra = 330.0 ;
Rp = 200.0 .
Ca regula absolut generala, drumurile adevarate si relevmenetele adevarate se masoara de la directia Na, in timp ce relevmentele prova se masoara doar de la axul prova al navei.
ATENTIE
Da = 000.o atunci cand nava se deplaseaza pe acelasi meridian catre N;
cand nava se deplaseaza pe acelasi paralel catre E atunci Da = 090.o;
cand nava se deplaseaza pe acelasi meridian catre S, atunci Da = 180.o;
cand nava se deplaseaza pe acelasi paralel catre W, atunci Da = 270.o.
Cand drumul adevarat al navei se gaseste in limitele 000.o < Da < 090.o atunci se spune ca drumul navei se afla in cadranul I de orizont (sau NE);
Cand drumul adevarat al navei se gaseste in limitele 090.o < Da < 180.o, se spune ca drumul navei se gaseste in cadranul II (sau SE) de orizont.
Cand drumul adevarat al navei se gaseste intre limitele 180.o < Da < 270.o se spune ca drumul se gaseste in cadranul III de orizont;
Cand drumul adevarat al navei se gaseste intre limitele 270.o <Da < 360.o, se spune ca drumul se gaseste in cadranul IV (sau NW) de orizont.
Incadrarea valorilor de relevment adevarat masurate la repere in cele patru cadrane de orizont este analoga regulii date pentru drumul adevarat. Astfel:
daca un reper se gaseste pe acelasi meridian cu nava, catre nord fata de aceasta, atunci Ra = 000.o, iar
daca valoarea relevmentului adevarat masurat la un reper se gaseste in limitele 000.o < Ra < 090.o atunci reperul se va vedea in cadranul NE (cadranul I) de orizont.
Relevmentele prova se masoara in sistem circular, conform definitiei, de la axa longitudinala-prova in sens retrograd (deci prin tribord intotdeauna), putand lua valori de la 000 la 360 , modul de notare fiind:
Rp = 045 .o; Rp = 135 .o; Rp = 270 .o
2) Sistemul semicircular este utilizat la scara mai restransa in navigatia moderna. In acest sistem, directia de referinta pentru masurarea unghiurilor poate fi, optional, directia nord adevarat sau directia sud adevarat. De asemenea, unghiurile (drumuri, relevmente etc.) se pot masura atat in sens retrograd cat si in sens direct, luand valori de la 000.o la 180.o.
Relevmentul prova exprimat semicircular se masoara de la axa longitudinala a navei in sens retrograd (prin tribord) sau in sens direct (prin babord), functie de bordul in care se vede reperul. Astfel, relevmentele prova semicirculare sunt intotdeauna mai mici de 180 si poarta indicele Td sau Bd ( tribord sau babord ).
Exemplu : RpBd = 0855 .
RpTd = 0855
3) Sistemul cuadrantal. In acest sistem:
Unghiurile se exprima precizand cadranul de orizont in care acestea se gasesc.
Directia de referinta este nord adevarat (pentru unghiuri situate in cadranele I si IV) sau sud adevarat (pentru unghiuri cu valori in cadranele II si III);
sensul de masurare poate fi direct sau retrograd, iar valoarea unui unghi exprimat cuadrantal nu poate depasi 090 (valoarea unui cadran).
Exemplu: Da = NE 046.5 ;
Ra = NW 048.o .
ATENTIE: Relevmentele prova nu se exprima in sistem cuadrantal.
Relatiile generale intre drumuri si relevmente (exprimate circular) sunt:
Ra = Da + Rp
Da = Ra - Rp
Rp = Ra - Da
Aceste relatii nu mai sunt valabile pentru relevmente prova exprimate semicircular. In aceasta situatie, se recomanda sa se utilizeze urmatoarele relatii:
Ra = Da + RpTd = Da - RpBd
Da = Ra - RpTd = Ra + RpBd
RpTd = Ra - Da
RpBd = Da - Ra.
Drumurile si relevmentele exprimate in sistemul cuadrantal se transforma in sistem circular folosind urmatoarele relatii:
|
Da (Ra) in sistem cuadrantal |
Da (Ra) in sistem circular |
|
Da(Ra) NEn |
Da(Ra) n |
|
Da(Ra) = SEn |
Da(Ra)=l80 - n |
|
Da(Ra) = SWn |
Da(Ra) = 180 + n |
|
Da(Ra) = NWn |
Da(Ra) = 360 - n |
4) Impartirea orizontului in carturi este de asemenea un sistem demodat, specific epocii velierelor. In acea perioada, data fiind precizia scazuta de masurare a unghiurilor in planul orizontului adevarat (Da, Ra, Rp), se utilizau pentru precizarea acestora carturile. Cartul este unitatea de masura pentru unghiuri reprezentand a 32-a parte din orizont deci 360/32 = 1115' = 111/4.
Fiecare cart are o denumire proprie, asa cum rezulta din fig.20, precum si un numar de ordine propriu de la 0 la 8 incepand de la N catre E si W, respectiv de la S catre E si W.
Exprimarea directiei (drumului sau relevmentului) se facea fie prin denumirea cartului, fie prin precizarea cadranului de orizont si a numarului de ordine a cartului din cadranul respectiv de orizont.
Carturile principale sunt :
-carturile N, E, S, W : acestea indica directiile cardinale ;
carturile NE, SE, SW, NW : acestea indica directiile intercardinale;
carturile NNE, ENE, ESE, SSE, SSW, WSW, WNW, NNW : acestea indica directiile inter-intercardinale.
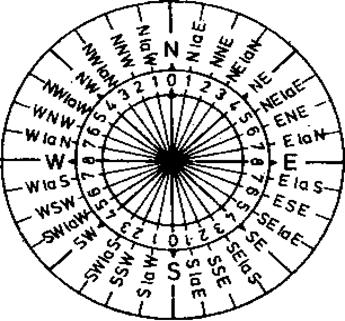
[ Fig.22 ] Impartirea orizontului in carturi
In prezent, sistemul de contare in carturi se mai utilizeaza doar pentru a indica, la precizie de cart inter-intercardinal, directia vantului. De asemenea, trebuie precizat ca sistemele semicircular si cuadrantal se mai utilizeaza in navigatia astronomica. De asemenea, relevmentele prova se exprima de regula semicircular, precizand bordul in care se vede reperul. In fig.22 este reprezentata schema de impartire a orizontului in carturi:
ORIZONTUL
1. ORIZONTUL GEOMETRIC
Definitia data planului orizontului adevarat al observatorului implica faptul ca acesta este infinit. Cu toate acestea, un observator A al carui ochi G se afla la inaltimea i fata de nivelul marii (vezi fig.23) vede orizontul sub forma de cerc, datorita sfericitatii Pamantului. Este deci necesar a se face distinctia intre notiunea de plan al orizontului adevarat si notiunea de orizont.
Se numeste orizont geometric locul geometric al punctelor de pe suprafata sferei terestre in care tangenta dusa din ochiul observatorului atinge suprafata acesteia. Orizontul geometric este deci un cerc mic ( BB', fig.23).
S-a notat cu d' distanta la orizontul geometric. Pentru calculul acestei distante, se aplica teorema lui Pitagora in triunghiul dreptunghic GBO :
![]()
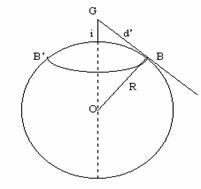
[ Fig.23 ] Orizontul geometric
Facand inlocuirile, rezulta:
![]()
Deoarece i2 << 2Ri , atunci:
![]()
In ultima relatie toate marimile din membrul drept sunt exprimate in [m].
Pentru a obtine pe d' in [Mm] , se exprima i si R in [Mm] si rezulta :
![]()
Deci : ![]()
relatie care da pe d' in [Mm], avand ca valoare de intrare pe i in [m].
2. ORIZONTUL VIZIBIL
Observatorul de la bordul navei, in conditiile existentei atmosferei terestre, vede un singur orizont - determinat de linia aparenta care separa marea de cer, denumit orizont vizibil sau orizontul marii.
Orizontul vizibil este situat mai departe decat orizontul geometric, datorita efectului refractiei terestre. Refractia terestra este fenomenul care cauzeaza devierea razei de lumina ce leaga doua puncte de la suprafata Pamantului, situate la altitudini diferite.
Pentru a explica elementele care definesc orizontul vizibil, in fig. 25 consideram observatorul A, in aceleasi conditii ca in fig. 23. Densitatea aerului in straturile inferioare ale atmosferei variaza invers proportional cu altitudinea; de aceea, o raza de lumina care pleaca din punctul D, aflat pe orizontului vizibil, trecand prin straturi atmosferice cu o densitate care scade cu altitudinea, este refractata si ajunge in ochiul observatorului A parcurgand o curba DA, denumita curba de refractie.
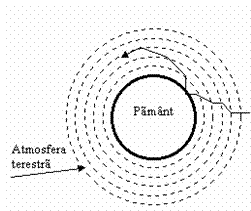
Fig 24. Refractia atmosferica
Curba de refractie DA (figura 25), are concavitatea spre Pamant si este continuta in planul vertical determinat de verticalele locului in punctele A' si D.
Observatorul considerat in A vede punctul D al orizontului marii pe directia AD', determinata de tangenta la curba de refractie in punctul A. curba de refractie avand concavitatea spre Pamant si fiind continuta in acelasi plan vertical, rezulta ca refractia terestra modifica numai inaltimea aparenta a obiectelor observate, fara a afecta relevmentele lor.
Unghiul format intre planul orizontului adevarat al observatorului (HH') si directia la orizontul vizibil (AD ) se numeste depresiunea orizontului vizibil (Depr.).
Refractia terestra este functie de diferenta de densitate a straturilor inferioare ale atmosferei; diferenta de densitate este dependenta in principal de temperatura, presiunea si umiditatea acestor straturi atmosferice. Orizontul vizibil se poate considera ca un cerc mic pe sfera terestra, in ipoteza ca refractia terestra este aceeasi pe intreg orizontul.
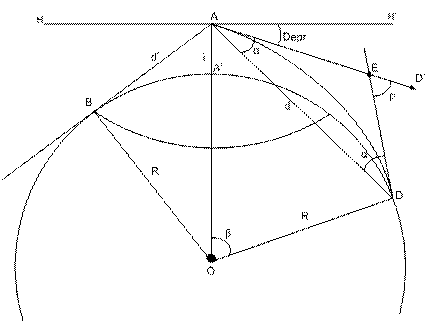
Figura 25. Orizontul vizibil
Repartitia orizontala neomogena a maselor de aer care constituie straturile inferioare ale atmosferei poate da nastere unei refractii terestre neuniforme, cu aparitia unei imagini frante sau deformate a liniei orizontului vizibil; fenomenul poarta denumirea de miraj, putand lua forme optice foarte diferite. De asemenea, o refractie anormala poate da nastere la fenomene surprinzatoare privind distanta la care sunt vizibile obiectele.
2.1 Determinarea distantei la orizontul vizibil
Pentru a face posibila determinarea cu exactitate a distantei la orizontul vizibil ar trebui sa se stabileasca cu rigurozitate traiectoria razei de lumina DA, adica a curbei de refractie terestra. Aceasta ar implica cunoasterea constitutiei atmosferei sau cel putin a legii variatiei densitatii, in diferitele ei straturi. Deoarece nu avem inca asemenea cunostinte despre atmosfera, studiul refractiei terestre si al efectelor ei nu se poate baza in prezent decat pe ipoteze.in consecinta, determinarea distantei d la orizontul vizibil se realizeaza prin stabilirea unei marimi aproximative, valabila pentru conditiile medii de refractie terestra, care se adauga la distanta d' la orizontul geometric.
Unghiul format intre tangentele la curba de refractie in punctele A si D, se numeste unghiul refractiei terestre (fig. 25). Marimea acestui unghi nu poate fi stabilita cu precizie din motivele aratate mai sus; marimea aproximativa a unghiului refractiei terestre ( ) se determina pe baza unor reguli stabilite experimental, care se verifica cu suficienta precizie numai pentru distante relativ mici, de ordinul a cateva mile marine, la diferente de altitudine pana la 25-30 m si numai in conditii atmosferice normale, care genereaza conditii medii de refractie terestra.
Aceste reguli, denumite legile refractiei terestre, sunt urmatoarele:
curba de refractie terestra AD se asimileaza cu un arc de cerc. Se admite deci ca triunghiul ADE este isoscel, iar unghiurile formate in A si D sunt egale. Notand acest unghi cu α, el se afla cu in urmatoarea relatie:
motiv pentru care este numit semiunghiul refractiei terestre;
unghiul refractiei terestre (ρ) este proportional cu unghiul β la centrul sferei terestre format intre verticalele punctelor A si D, respectand urmatoarea relatie:
ρ=k β sau ρ=2γ β
Coeficientul γ este numit coeficientul refractiei tereste , valoarea lui variind intre 0.04 si 0.15-in functie de conditiile atmosferice. Pentru o stare atmosferica normala, care genereaza conditii medii de refractie terestra, se considera cu valoarea sa medie de 0.08
Din relatiile de mai sus se observa ca semiunghiul refractiei terestre poate fi exprimat de egalitatea:
Distanta la orizontul vizibil (d) se considera mai mare decat distanta la orizontul geometric (d') cu o marime in functie de semiunghiul refractiei terestre (α):
d = d'+
Pentru precizia necesara calculului, masura unghiului β in minute de arc poate fi considerata egala cu distanta d ' la orizontul geometric exprimata in mile marine.
Deci:
d = d'+ γ d'=d(l+ γ)=l.08d'
Cunoscand formula de determinare a distantei la orizontul geometric obtinem:
Avand in vedere relatia care exprima pe d', obtinem;

relatie care se utilizeaza pentru calculul distantei la orizontul vizibil in mile marine functie de inaltimea ochiului observatorului in metri.
Distanta la orizontul vizibil se poate determina expeditiv si cu tabla nr.5a, pag.31, DH-90. Se intra pe coloana din stanga cu valoarea inaltimii ochiului in metri iar valoarea distantei la orizontul vizibil in mile marine se determina corespunzator pe coloana din dreapta.
Formula de calcul a distantei la orizontul vizibil este rezolvata si de tabla "Distance of sea horizon in nautical miles ' din Brown's Nautical Almanac(dar inaltimea ochului observatorului este exprimata in picioare).
d [Mm] 1,15![]()
La bordul navelor maritime de transport, a caror linie de plutire are variatii considerabile in functie de starea de incarcare, se impune a se stabili si afisa in camera hartilor - inaltimea puntii de comanda si a puntii etalon, de unde se fac observatiile in navigatie deasupra liniei de plutire, la diferite pescaje; pentru a stabili inaltimea ochiului observatorului deasupra nivelului marii, ramane ca navigatorul sa adauge inaltimea proprie la inaltimea puntii de observatie deasupra liniei de plutire
Exemplu: Sa se determine cu tabla 5a DH-90 valoarea distantei la orizontul vizibil pentru
1) i = 7m ;
2) i = 53 m .
Rezolvare
1) d = 5.5 Mm . (se intra pe coloana din stanga cu i=7m si corespunzator pe coloana din dreapta se va gasi valoarea 5.5);
2) d = 15.1 Mm .(valoarea i=53m nu exista in tabla, si ca urmare valoarea lui d se va interpola dupa urmatoarea schema):
i = 52 ----> d = 15
i = 53 ----> x
i = 54 ----> d = 15.3 ===>x = d = 15.15 Mm.
OBSERVATIE: Distanta la orizontul vizibil nu constituie linie de pozitie in navigatie, sau, cu alte cuvinte, cu valoarea lui d nu se determina pozitia navei. Calculul valorii distantei la orizontul vizibil nu are un suport de precizie necesar acestui lucru datorita faptului ca ea depinde de parametrii atmosferici instantanei. Distanta la orizontul vizibil are doar un rol orientativ pentru navigator.
Distanta la orizontul vizibil se poate determina expeditiv si cu tabla nr.5a, pag.31, DH-90. Se intra pe coloana din stanga cu valoarea inaltimii ochiului in metri iar valoarea distantei la orizontul vizibil in mile marine se determina corespunzator pe coloana din dreapta.
Exemplu: Sa se determine cu tabla 5a DH-90 valoarea distantei la orizontul vizibil pentru
1) i = 7m ;
2) i = 53 m .
Rezolvare
1) d = 5.5 Mm . (se intra pe coloana din stanga cu i=7m si corespunzator pe coloana din dreapta se va gasi valoarea 5.5);
2) d = 15.1 Mm .(valoarea i=53m nu exista in tabla, si ca urmare valoarea lui d se va interpola dupa urmatoarea schema):
i = 52 ----> d = 15
i = 53 ----> x
i = 54 ----> d = 15.3 ===>x = d = 15.15 Mm.
OBSERVATIE: Distanta la orizontul vizibil nu constituie linie de pozitie in navigatie, sau, cu alte cuvinte, cu valoarea lui d nu se determina pozitia navei. Calculul valorii distantei la orizontul vizibil nu are un suport de precizie necesar acestui lucru datorita faptului ca ea depinde de parametrii atmosferici instantanei. Distanta la orizontul vizibil are doar un rol orientativ pentru navigator.
3. ORIZONTUL DE RADIOLOCATIE
Determinarea distantei la orizontul de radiolocatie prezinta de asemenea o importanta deosebita pentru navigator, valoarea acesteia reprezentand o informatie pretioasa in legatura cu cele mai indepartate puncte de la care radiolocatorul mai primeste semnal ecou.
Distanta la orizontul de radiolocatie depinde de inaltimea antenei de radiolocatie (h), iar coeficientul ce intra in calcul s-a determinat plecand de la aceleasi premize ca si in cazul distantei la orizontul vizibil. Coeficientul de refractie (t) este dublu pentru undele electromagnetice cu lungimi de unda radar (centimetrice). Ca urmare, relatia de calcul a distantei la orizontul de radiolocatie este:
dr [Mm] = 1.93(1+0.15)![]() = 2.224
= 2.224![]()
Relatia este evident aproximativa, valoarea reala depinzand de parametrii atmosferici si tehnici. Pentru calcule expeditive se recomanda utilizarea tablei nr.5b pag.31 DH-90; modul de lucru este acelasi ca la paragraful precedent.
4. DISTANTA LA CARE UN OBIECT APARE LA LINIA ORIZONTULUI
In fig.26 este reprezentata o nava care se deplaseaza catre reperul de inaltime H . Ochiul observatorului de pe puntea de comanda a navei are inaltimea i.
Este evident ca distanta la care reperul va apare la linia orizontului, si care se noteaza cu DT va fi suma distantelor la orizontul vizibil calculate pentru reper (dH) si pentru observator (di):
DT =
dH + di = 2.08![]() + 2.08
+ 2.08![]() = 2.08
= 2.08![]() .
.
Relatia este valabila pe timp de noapte, cand lumina farurilor se distinge relativ usor la linia orizontului. Pe timpul zilei insa, este necesar ca nava sa parcurga un spatiu suplimentar pentru ca varful reperului sa se distinga la linia orizontului. Se considera ca distanta la care apare reperul la lina orizontului pe timpul zilei este mai mica decat cea calculata pentru perioada de intuneric cu cca. 2%. Rezulta ca relatia de calcul va fi :

[Fig.26]
Distanta la care apare un obiect la linia orizontului
DT =
2.04(![]() )
)
Pentru determinarea rapida a distantei la care un obiect apare la linia orizontului, se recomanda a se utiliza tabla nr.6 pag.32 DH-90. Se arata mai jos modul de utilizare al tablei pe un exemplu practic:
Exemplu: Sa se determine distanta la care un reper de inaltime H=75m apare la linia orizontului pentru un observator cu i = 12m .
Rezolvare : DT = 25.2 Mm ; Pentru determinarea lui DT se intra la pag.32 in tabelul din partea de jos a paginii pe coloana i=12 si, datorita faptului ca valoarea H=75m nu se gaseste in tabla, se va face urmatoarea interpolare simpla :
pentru i=12 si H= 70m .DT = 24.6 Mm
H= 75m .x
H= 80m .DT = 25.8 Mm
Rezulta ca x = DT = 25.2 M.
Acelasi rezultat se obtine daca se face interpolarea cu ajutorul tablei 62 din DH-90, tabla 'Parti proportionale'.
Mai trebuie precizat ca pe hartile marine, alaturi de reperele de navigatie sunt trecute si caracteristicile acestora, intre care si distanta in [Mm] la care lumina acestora apare la linia orizontului in ochiul unui observator cu inaltimea de 5m; aceasta valoare se numeste bataie geografica a farului si se noteaza cu Dharta. Relatia de calcul a DT, utilizand valoarea bataii geografice data in harta este:
DT [Mm]
= Dharta [Mm] - 4.7 [Mm] + 2,08![]() .
.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 5257
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved