DETERMINAREA DRUMULUI DE VALOARE OPTIMA INTR-UN GRAF

DETERMINAREA DRUMULUI DE VALOARE OPTIMA INTR-UN GRAF

Fie graful G = (X,F) =(X,A).

Pentru determinarea drumului de valoare optima (minima sau maxima) dintre doua varfuri x_i si x_j ale grafului G, asociem fiecarui arc un numar real pozitiv notat v (x_i, x_j) numit valoarea arcului.

In functie de problema economica transpusa in termenii teoriei grafurilor, valoarea arcului poate reprezenta: costul de fabricatie al unui produs intr-un anumit loc de munca asociat cu arcul (x_i, x_j); productivitatea muncii intr-un loc de munca, costul sau durata transportului pe ruta (x_i, x_j) etc.

Fie drumul d = (a₁, a₂, ., a_p), unde a_k reprezinta un arc component al drumului. . Marimea v(d) definita prin egalitateaL v(d) = se numeste valoarea drumului d. (Valoarea drumului este egala cu suma valorilor arcelor care-l compun.).

Algoritmul Bellman - Kalaba de determinare a drumului optim intr-un graf fara circuite

Ipoteza: drumul optim este format din arce a_icare leaga nodul initial x₁ cu nodul final x_n.

Algoritmul de determinare a drumului optim difera in functie de tipul problemei: aflarea drumului de valoare minima sau aflarea drumului de valoare maxima.

Algoritm de determinare a drumului de valoare minima

Fie graful G = (X,F) =(X,A).

Asociem grafului G matricea C = (c_ij), i,j = unde:

C_ij =

Fiecarui varf x_i i se asociaza o variabila v_i care reprezinta valoarea drumului care uneste varful x_i cu x_n.

Elementele matricei C se trec intr-un tabel care contine pentru inceput x_n linii si x_n coloane. ( tabelul se va completa ulterior cu alte linii pe masura parcurgerii algoritmului.

Valoarea minima a drumului care uneste pe x₁ cu x_n se obtine rezolvand sistemul de ecuatii:

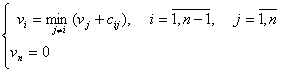
Daca cu i = este solutie a sistemului de mai sus, atunci reprezinta valoarea minima a drumului care uneste pe x₁ cu x_n.

Pentru rezolvarea sistemului, se procedeaza iterativ.

Pasul care initiaza procesul iterativ este definit de:

v, i =

si v

La iteratia (pasul) k , kvom rezolva sistemul:

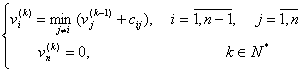
Procesul se incheie cand se obtine v, i=. In acest caz, valoarea minima a drumului care uneste  x₁ cu x_n este .

Determinarea arcelor (sau varfurilor) care compun drumul de valoare minima:

Fie xvarful pentru care : v.

Drumul de lungime minima trece prin xsi v reprezinta valoarea minima a drumului care uneste xcu x_n. Mai departe, fie:

vRezulta ca drumul minim trece prin x. Repetam procedeul pornind de la v pana ajungem la o valoare v.

Drumul de valoare minima este d = (x, x, x, , x, x)

Pentru determinarea drumului de valoare maxima intre varfurile x₁ si x_n ale grafului G folosind algoritmul Bellman - kalaba se fac urmatoarele modificari:

in matricea C, consideram c_ij = -, daca (x_i, x_j), pentru i;

in toate sistemele de ecuatii, operatorul de minim se inlocuieste cu cel de maxim.

Exemple

1. Sa se determine drumul de valoare maxima al grafului:

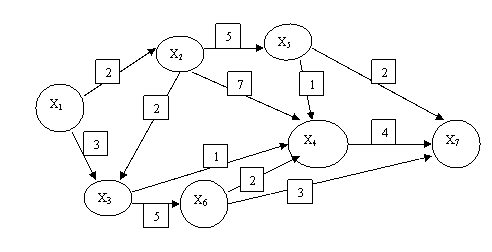
Pasul 1

Se alcatuieste un tabel care contine pe prima linie si pe prima coloana nodurile (varfurile) grafului si in interior arcele care se formeaza la intersectia elementelor de pe linia 1 cu cele de pe coloana 1.

Tabelul se completeaza dupa urmatoarele reguli :

Daca exista arc (x_i, x_j) se trece valoarea arcului (lungimea)

Daca nu exista arc (x_i, x_j) se completeaza cu - ( numai la problemele de maxim)

Pentru i = j adica arce de forma (x_i, x_i) se completeaza cu 0.

Vom obtine:

Pasul 2

Fiecarui varf x_i i se asociaza o variabila v_i care reprezinta valoarea drumului care uneste x_i cu x_n.

Variabilele v_i se calculeaza in mai multi pasi, numarul pasului trecandu-se in partea dreapta sus, in paranteza, si pentru fiecare v se completeaza o linie in completarea tabelului initial.

Prima variabila este v si se obtine din transpunerea ultimei coloane corespunzatoare ultimului varf. In cazul nostru, vom transpune (adica scrie ca linie, coloana lui x₇)

Pasul 3

Se calculeaza valorile v respectiv v care se trec pe urmatoarea linie a tabelului.

Formula de calcul a valorilor v este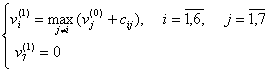

Calcularea lui v: se aduna linia v cu linia corespunzatoare lui x₁ (prima linie), element cu element, mai putin v cu c₁₁, si se alege valoarea maxima dintre sumele rezultate.

v

v

v

v

v si aceasta valoare se trece in tabel .

Calcularea lui v: se aduna linia v cu linia corespunzatoare lui x₂ (a doua linie), element cu element, mai putin v cu c₂₂, si se alege valoarea maxima dintre sumele rezultate

v

v

v

v

v si se trece rezultatul in tabel.

Analog se calculeaza si celelalte valori ale lui v si se obtine:

v 5

v 4

v 5

v 6

Iar v prin conventie.

OBS: Algoritmul se incheie daca se obtin doua linii corespunzatoare valorilor lui v_i egale ( la 2 pasi consecutivi)

Deoarece v vom continua algoritmul prin calcularea lui v

Pasul 4

Se calculeaza v dupa formula:

v

Vom obtine:

v

v

v

v

v

v

v 0 prin conventie.

Cu aceste valori obtinute se completeaza tabelul cu inca o linie, respectiv linia lui v

Deoarece v algoritmul se continua prin calcularea valorilor lui v

Pasul 5

Se calculeaza v

Si se obtine:

v

v

v 11

v 4

v 5

v 6

v 0

Deoarece v algoritmul se continua prin calcularea lui v

Pasul 6

Calculam v

Obtinem:

v 15

v 13

v 11

v 4

v 5

v 6

v 0

Deoarece v algoritmul se continua prin calcularea lui v

Pasul 7

Calculam v

Si obtinem:

v 15

v= 13

v 11

v 4

v 5

v 6

v 0

Algoritmul se incheie deoarece v.

Forma finala a tabelului este

Interpretarea rezultatelor:

Din tabelul intocmit obtinem 2 informatii:

1. Care este valoarea drumului maxim de la x₁ la x₇

Care sunt varfurile care compun drumul maxim.

Valoarea drumului maxim este 15 ( valoarea lui v de la ultimul pas)

Drumul de valoare maxima este:

d_max = (x_1, x₂, x₃, x₆, x₄, x₇)

Sa se determine drumul de valoare minima de la x_l la x₅ al grafului:

G = (X,A), X = A = avand urmatoarele lungimi de arce v(x₁, x₂) = 3, v(x₁, x₃) = 1, v(x₁, x₅) = 9, v(x₂, x₄) = 1, v(x₂, x₅) = 4, v(x₃, x₂) = 2, v(x₃, x₄) = 4, v(x₃, x₅) = 6, v(x₄, x₅) = 2.

R:

Lungimea drumului minim este 6 si exista doua drumuri minime:

d_1min = (x₁, x_2, x₄, x₅)

d_2min = (x₁, x₃, x₂, x₄, x₅)

PROBLEME :

1. Sa se afle drumul de valoare maxima de la x₁ la x₅ in graful G = (X,A), X = , A = daca v(x₁, x₂) = 5, v(x₁, x₃) = 2, v(x₁, x₄) = 2, v(x₂, x₅) = 1, v(x₃, x₂) = 4, v(x₄, x₂) = 3, v(x₄, x₃) = 3, v(x₄, x₅) = 2.

2. Sa se afle drumul de valoare minima al grafului G = (X,A) , X = , A = daca valorile arcelor sunt respectiv 8; 4; 6; 9; 1; 6; 1; 8; 2; 5; 7; 3.

3. Se considera graful valuat G = (X,A), X = , F(x₁) = , F(x₂) = , F(x₃) = , F(x₄) = , F(x₅) = , cu v(x₁, x₂) = 5, v(x₁, x₃) = 3, v(x₁, x₄) = 4, v(x₂, x₃) = 3, v(x₂, x₄) = 1, v(x₂, x₅) = 5, v(x₃, x₄) = 3, v(x₃, x₅) = 4, v(x₄, x₅) = 4.

Sa se arata ca G nu are circuite si sa se afle drumul de valoare maxima de la x₁ la x₅.

4. Fie graful G= (X,A), X = , F(x₁) = , F(x₂) = , F(x₃) = ,

F(x₄) = , F(x₅) =

a)            folosind matricea drumurilor sa se arate ca G nu are circuite si are drum hamiltonian ;

b)            stiind ca v(x₁, x₃) = 3, v(x₁, x₄) = 2, v(x₂, x₄) = 3, v(x₃, x₂) = 4, v(x₃, x₄) = 1, v(x₃, x₅) = 4, v(x₄, x₅) = 2 sa se arate ca d_H este drumul de valoare maxima de la x₁ la x₅.

5. a) Folosind matricea drumurilor sa se arate ca graful valuat G = (X,A), X = , A = avand valorile arcelor egale respectiv cu 3 ; 1 ; 2 ; 11 ; 7 ; 10 ; 9 ; 5 ; 4 ; 8 nu are circuite si are drum hamiltonian.

b) Sa se arate ca d_H este drumul de valoare maxima de la x₁ la x₅.