FUNCTII NUMERICE IN LabVIEW

FUNCTII NUMERICE IN LabVIEW

Obiectivele lucrarii

a)      Insusirea modului de utilizare a functiilor numerice ale mediului de programare

graphicLabVIEW.

b)      Realizarea pricipalelor operatii aritmetice,trigonometrice,logaritmice,complexe si

logice.

2.Aparatura si suporturile utilizate:

a) PC in configuratia unitate centrala,monitor, tastatura;

b) Precizarile din prezentul indrumar;

c) Manual de prezentare a mediului de programare grafic LabVIEW

3.Breviar

Functiile numerice se gasesc in paleta de functii ale diagramei conform figurii 1.

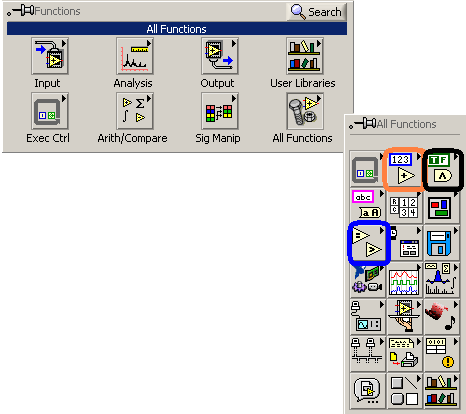
Figura 1. Locatiile functiilor numerice in paleta de functii.

La trecerea mouse-ului deasupra pictogramei incercuite cu rosu va aparea o paleta cu functii numerice ca in figura 2.

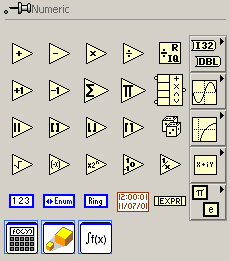
Figura 2. Functiile numerice ale mediului LabVIEW.

Prezentam in continuare unele din cele mai utilizate functii ale acestei palete si a subpaletelor incluse:

- adunare - inmultire

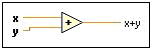
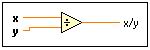- scadere - impartire

Acestea sunt functii polimorfice, acceptand la intrare valorile x si y care pot apartine

mai multor tipuri de date (scalari, matrici, siruri) rezultatul apartinand aceleasi clase.

Rezultatul operatiei x/y este exprimat de un numar cu punct flotant dubla precizie daca x si y sunt intregi, sau cea mai cuprinzatoare reprezentare pentru x si y cand acestea nu sunt intregi sau sunt de tipuri diferite.

- incrementare - decrementare

Acestea sunt functii polimorfice care aduna respectiv scad 1 la valoarea de intrare.

- adunare matriceala - inmultire matriceala

Acestea realizeaza suma, respectiv produsul tuturor elementelor din matricea numerica de la intrare.

- valoarea absoluta - signum

Functia polimorfica valoare absoluta returneaza la iesire valoarea absoluta a intrarii x care poate fi atat scalar cat si matrice , sir, etc, pe cand functia signum ne va da la iesire 1 cand valoarea de intrare este mai mare decat 0, 0 pentru o intrare egala cu 0, -1 pentru o intrare mai mica ca 0.

- rotunjire la intreg - rotunjire la +∞

- rotunjire la -∞

In cadrul programului LabVIEW se poate face rotunjirea unei valori fie la cel mai apropiat numar intreg (atat 1.5 cat si 2.5 se rotunjesc la 2) cat si la infinit cu + sau - (3.8 rotunjit la +INF va fi 4, iar rotunjit la -INF va fi 3).

- radical - reciproca

Functia radical (sqrt) calculeaza radacina patrata a valorii de la intrare. Daca x este negativ, rezultatul afisat va fi "NaN" cu exceptia cazului in care x este numar complex. In cazul in care x este un intreg, iesirea va fi de tipul numar cu punct flotant dubla precizie.

Reciproca il divide pe 1 cu intrarea x. Daca x=0, 1/x va fi infinit.

- generator de numere aleatoare

Produce la iesire un numar, exclusiv intre 0 si 1,an format numar cu punct flotant dubla precizie. Distributia este uniforma.

- constanta numerica - negatia

Functia negatie este o functie polimorfica care neaga valoarea intrarii.

Functia constanta se utilizeaza la introducerea valorilor numerice necesare in diagrama bloc. Valoarea se seteaza dand dublu clic in campul respectiv si introducand cifrele de la tastatura. Daca se introduce o valoare tip numar cu punct flotant, automat acesta va fi reprezentat ca fiind si dubla precizie. Daca se introduce un intreg, acesta va fi considerat tip intreg lung. Constantelor li se pot adauga etichete dar nu pot fi modificate in timpul functionarii instrumentelor virtuale.

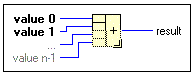
- functia aritmetica compusa - expresia compusa

Dupa cum sugereaza si numele, functia aritmetica compusa executa diverse operatii aritmetice (adunare, inmultire,SI,SAU) asupra a doua sau mai multe numere (scalari, siruri, expresii booleene). Operatiile se aleg executand clic dreapta pe functie si selectand "Change Mode". De asemenea se poate seta fiecare intrare in parte sa fie normala sau inversata (echivalentul negarii pentru operatiile logice).

Expresia compusa se utilizeaza la calculul expresiilor sau a ecuatiilor care desi contin o singura variabila (x) sunt stufoase sau complicate. Intrarea x poate fi teoretic de orice tip.

In cadrul paletei cu functii numerice exista mai multe subpalete : paleta cu functii de conversie, paleta cu functii trigonometrice, paleta cu functii logaritmice, paleta cu functii pentru numere complexe si paleta cu constante numerice aditionale.

Paleta cu functii trigonometrice este prezentata in figura 3.

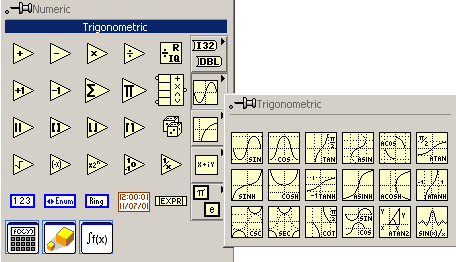
Figura 3. Functiile trigonometrice ale mediului LabVIEW.

si contine urmatoarele functii : sinus, cosinus, tangenta, sinus hiperbolic, cosinus hiperbolic, tanganta hiperbolica, cosecanta, secanta, cotangenta, arcsinus, arccosinus, arctangenta etc.

Paleta cu functii logaritmice este prezentata in figura 4.

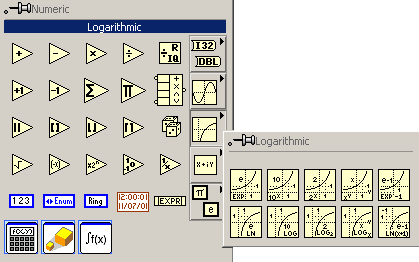
Figura 4. Functiile logaritmice ale mediului LabVIEW.

si contine urmatoarele functii : e^x, 10^x, 2^x, x^y, ln(x), log(x), log2(x), logx(y) etc.

Paleta cu functii pentru numere complexe este prezentata in figura 5.

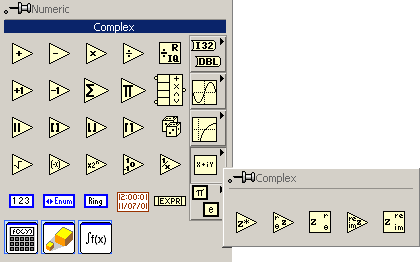
Figura 5. Functiile pentru numere complexe ale mediului LabVIEW.

si contine urmatoarele functii : o functie pentru obtinerea conjugatei, o functie pentru transformarea din polar in complex, o functie pentru transformarea din complex in polar, o functie pentru crearea unui numar complex din partea reala si cea imaginara si o functie pentru extragerea partii reale si a celei imaginare dintr-un numar complex.

Paleta cu constante numerice aditionale este cea din figura 6.

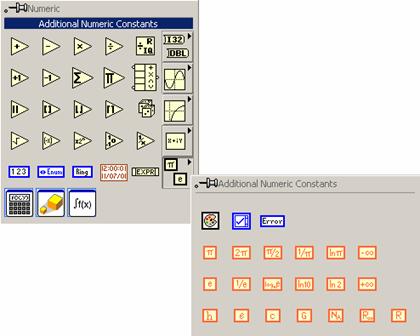
Figura 6. Constante numerice aditionale ale mediului LabVIEW.

Aceasta contine o serie de constante uzuale predefinite din care amintim : pi cu multipli si submultipli uzuali, numarul e, +/-∞, logaritmul natural al lui pi, 2, 10, etc.

La trecerea mouse-ului deasupra pictogramei incercuite cu negru din figura 1 va aparea o paleta cu functiile logice din figura 7.

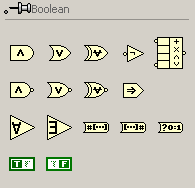
Figura 7. Functiile logice ale mediului LabVIEW.

Aceasta contine urmatoarele functii logice : SI, SAU, SAU EXCLUSIV, NEGATIE, SI NEGAT, SAU NEGAT, SAU EXCLUSIV NEGAT etc.

La trecerea mouse-ului deasupra pictogramei incercuite cu albastru din figura 1 va aparea o paleta cu functii pentru realizarea comparatiilor ca in figura 8.

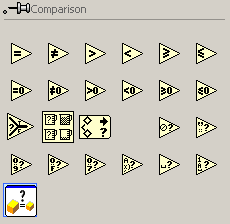
Figura 8. Functiile pentru realizarea comparatiilor ale mediului LabVIEW.

Aceasta contine functii pentru realizarea urmatoarelor comparatii : egalitate, inegalitate, mai mare, mai mic, mai mare sau egal, mai mic sau egal, egal cu 0, diferit de 0, mai mare ca 0, mai mic ca 0, mai mare sau egal cu 0, mai mic sau egal cu 0 etc.

4. Modul de lucru

a) Se alimenteaza sistemul cu tensiune;

b) Se lanseaza mediul LabVIEW;

c) Se implementeaza programul P1 descris in prezenta lucrare.

Programul P1 rezolva o ecuatie de gradul al II-lea.

Pe panou se vor pune urmatoarele elemente evidentiate in figura 9 :

trei obiecte Num Ctrl pentru introducerea celor trei coeficienti ai ecuatiei: a, b, c;

sapte obicte Num Ind pentru afisarea lui Δ, a solutiilor reale ale ecuatiei, respectiv a

partilor reale si imaginare ale solutiilor complexe ele ecuatiei;

patru obiecte String Ind pentru afisarea tipului solutiei, pentru a permite afisarea

solutiilor complexe si a unui mesaj care sa indice existenta/inexistenta unei ecuatii de gradul al II-lea;

trei leduri care ajuta la indicarea tipului solutiei si a tipului mesajului.

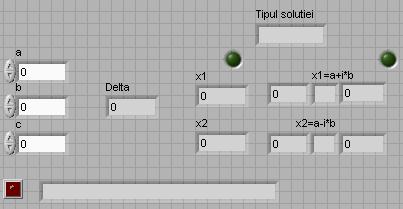
Figura 9. Elementele de pe panou corespunzatoare programului P1.

In diagrama se vor introduce urmatoarele functii evidentiate in figura 10

functiile Negate, Add, Substract, Multiply, Divide, Square Root, Greater Or Equal

To 0 , Greater Then 0 , Not Equal To 0?, Not, Select utilizate pentru calculul solutiilor ecuatiei;

constante numerice si de tip sir de caractere utilizate la calculul solutiilor si la

reprezentarea acestora.

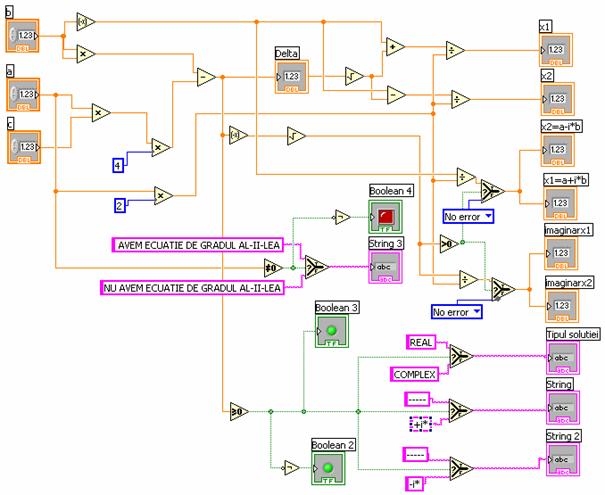
Figura 10. Diagrama programului P1.

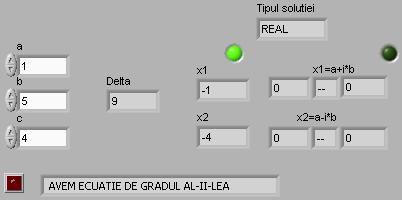
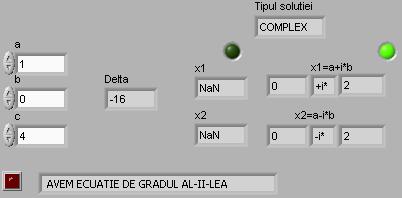
Figura 11. Rezultatele executiei programului P1.

5. Exercitii

1) Sa se realizeze un program in LabVIEW care sa calculeze expresia

.

2) Sa se realizeze un program care sa simuleze numeric aruncarea a doua zaruri.