| CATEGORII DOCUMENTE |
INTRODUCERE IN ALGORITMICA
1.1. Notiunea de algoritm
Solutia unei probleme, din punct de vedere informatic, este data printr-o multime de comenzi (instructiuni) explicite si neambigue, exprimate intr-un limbaj artificial. Notiunile fundamentale privind rezolvarea problemelor cu ajutorul calculatorului sunt: algoritm, limbaj de programare, program.
Ati putea da exemple de algoritmi? In caz afirmativ, incercati o descriere a unui algoritm.
Cum adunati doua numere naturale, exprimate in sistemul zecimal, a cate 10 cifre?
Exista mai multe definitii ale notiunii de algoritm[1]. A. A. Markov, a considerat algoritmul ca fiind o notiune matematica primara si a descris-o astfel:
Un algoritm este o reteta care descrie precis si clar un proces de calcul.
El a descris un mecanism formal pentru a specifica o clasa larga de activitati si anume algoritmii normali. Alte modalitati de descriere a algoritmilor ce au mai fost propuse sunt: masina Turing, sistemele Post, functiile recursive etc. In cadrul acestui curs, prin algoritm vom intelege o secventa finita de comenzi explicite si neambigue care, executate pentru o multime de date (ce satisfac anumite conditii initiale), conduce in timp finit la rezultatul corespunzator. Observam ca se face distinctie intre algoritm (care se termina in timp) si procedura (care poate continua nedefinit). Conform lui D. Knuth [4], un algoritm poseda cinci caracteristici importante:
Un algoritm are caracter finit. El
este descris printr-o secventa finita de etape si
trebuie ca, ori de cate ori sunt parcurse etapele algoritmului pentru
anumite date, procesul sa se incheie in timp finit. Un algoritm are caracter determinist.
Actiunile specificate de pasii algoritmului sunt clare, fiind
riguros prezentate. Un algoritm are sau nu date de intrare.
Se poate admite ca intotdeauna un algoritm lucreaza asupra unor
date de intrare. Acestea pot fi evidentiate din contextul in care este
formulata problema a carei solutie o reprezinta
algoritmul. Un algoritm furnizeaza cel
putin o valoare de iesire ce se afla intr-o relatie
specifica cu datele de intrare. Un algoritm este eficace.
Trebuie spus ca nu orice problema admite solutie descrisa algoritmic. Problemele pentru care exista un algoritm de rezolvare se numesc probleme decidabile. Problemele pentru care s-a demonstrat (matematic) ca nu admit un algoritm de rezolvare se numesc probleme nedecidabile.
Exemplul 1.1. Fie f = a0 + a1X + + anXn, un polinom cu coeficienti intregi. Se poate stabili existenta unei solutii (in multimea numerelor) intregi a ecuatiei f(x)=0? Raspunsul este afirmativ. Se poate demonstra ca daca p este o radacina intreaga a lui f atunci p este un divizor al termenului liber a0. Deci, este suficient sa analizam elementele multimii divizorilor (pozitivi si negativi) termenului liber si sa verificam daca printre acestea sunt si radacini ale polinomului f. Cum multimea divizorilor unui numar intreg este finita, exista un numar finit de verificari si deci procedura descrisa este un algoritm.
Dati exemple de probleme decidabile. Admit o unica metoda de rezolvare sau mai multe?
Exemplul 1.2. In domeniul programarii calculatoarelor o problema foarte importanta o constituie studiul corectitudinii programelor. Mai precis:
Fiind date un program P si o anumita configuratie a datelor de intrare, ajunge programul P la configuratia de iesire corecta in timp finit?
Desi pentru un numar mare de programe aceasta problema este decidabila, la nivelul tuturor programelor, este o problema nedecidabila.
Adica:
Nu exista un algoritm care sa determine daca un program arbitrar se termina pentru o configuratie a datelor de intrare.
Deci:
Problema corectitudinii nu este decidabila la nivelul tuturor programelor de calculator.
O demonstratie a acestei afirmatii este data, de exemplu, in [3].
Ce implicatii practice are rezultatul din exemplul 1.2 ?
Exemplul 1.3. Fie x un numar irational si (a0, a1a2an) scrierea sa infinita in baza zece. Formam sirul (pn)n>0 astfel: daca ak este prima zecimala nula in scrierea lui x atunci punem pk = 0 si p1 = p2 = = pk-1 = 1. Pana la prima zecimala nenula punem in sirul (pn) valoarea zero. Pe pozitia zecimalei nenule imediat intalnite punem valoarea 2 si continuam sa punem 2 pana la urmatoarea zecimala nula. Acest procedeu continua pentru toate zecimalele lui x. Deci, daca numerele din sirul (pn) ce preced un sir de zerouri consecutive sunt egale cu t, atunci numerele ce urmeaza ultimului zero pana la urmatorul zero intalnit sunt egale cu t+1. Se demonstreaza (Novikov P.S. [5]) ca exista un unic numar care va apare in sir de o infinitate de ori. Totusi nu se poate determina efectiv acest numar deoarece nu stim daca in scrierea lui x exista o infinitate de zerouri.
Incheiem aceste exemple cu urmatoarea remarca.
Nu este suficient ca o anumita problema (clasa de probleme) sa admita solutii (chiar si o singura solutie). Din punctul de vedere al informaticii, intereseaza daca exista solutie ce poate fi descrisa algoritmic, deci daca solutia problemei poate fi construita efectiv. De asemenea, pentru rezolvarea anumitor probleme pot exista mai multi algoritmi. Stabilirea celui mai bun dintre acestia se realizeaza in urma unui proces de analiza prin care se determina performantele fiecaruia dintre algoritmi.
In finalul acestei sectiuni vom descrie cativa algoritmi elementari. Acestia vor contribui la realizarea unui prim contact cu solutiile algoritmice. Mai intai evidentiem cateva conventii.
Datele supuse prelucrarilor sunt manipulate cu ajutorul variabilelor. Acestea sunt entitati ce pot referi elemente ale unei anumite multimi. Putem vorbi de variabile intregi (respectiv reale, caracter etc.) atunci cand acestea se refera la valori intregi (respectiv reale, caracter etc.).
Actiunile realizate in cadrul unui algoritm vor fi descrise prin verbe: executa, citeste, scrie etc.
Notatiile matematice consacrate vor fi utilizate fara explicatii suplimentare.
Vom utiliza constructii precum: daca, atunci, altfel, cat timp, repeta, pana cand, pentru, de la, pana la etc., a caror semnificatie este cea uzuala.
O operatie importanta este aceea prin intermediul careia o variabila "va primi" o anumita valoare. Aceasta actiune se mai numeste operatie de atribuire si, in continuare, se va nota prin ":=" Valoarea ce se atribuie unei variabile este rezultatul evaluarii unei expresii. Expresia poate fi de tip numeric sau de tip logic. Intr-o expresie numerica apar numere (intregi, reale etc.) si operatori aritmetici precum: + (adunare), - (scadere), * (inmultire), / (impartire) etc. Expresiile logice (numite si expresii booleene) contin operatori logici: and (si logic), or (sau logic), not (negatie) si operatori relationali (<, >, <= (mai mic sau egal), >= (mai mare sau egal), != sau <> (diferit), = (egalitate)) folositi intre elemente pentru care aceste operatii au sens. Rezultatul evaluarii unei expresii logice poate fi: true (adevarat) sau false (fals). In descrierea unei expresii pot fi folosite si alte simboluri daca acestea sunt cunoscute sau explicate. Utilizarea parantezelor: "(" si ")" pentru indicarea modului de evaluare este, de asemenea, permisa.
Am vazut ca algoritmii accepta date de intrare si furnizeaza rezultate (date de iesire).
Introducerea unei valori sau a unui sir de valori se va descrie folosind verbul citeste. Afisarea unei valori sau a unui sir de valori va fi descrisa prin verbul scrie.
Vom conveni sa numerotam pasii (etapele) unui algoritm. Aceasta numerotare va fi utilizata eventual in alti pasi. Acest mod de prezentare a algoritmilor se numeste descriere in limbaj conventional. In unele lucrari, limbajul conventional mai este numit si limbaj pseudocod.
Exemplul 1.4. Fie a si b doua variabile intregi. Dorim sa schimbam intre ele valorile celor doua variabile. Mai precis, daca a = 640 si b = 480, dorim sa obtinem a = 480 si b = 640.
Un mod de a realiza aceasta schimbare presupune utilizarea unei variabile suplimentare, cu rol de intermediar. Folosind trei operatii de atribuire, algoritmul are urmatorii pasi [1], [2]:
1. Salveaza valoarea initiala a variabilei a in variabila t.
2. Stocheaza in (atribuie lui) a valoarea initiala a variabilei b.
3. Stocheaza in b valoarea initiala a variabilei a care, acum, se afla in variabila t.
1. citeste a, b 2. t := a 3. a := b 4. b := t 5. scrie
a,b
Lasam ca exercitiu realizarea urmatoarelor transformari:
i) a --> b --> c --> a
ii) a --> b --> c --> d --> a
Atunci cand va fi necesar, ne vom referii la pasii 2, 3 si 4 prin constructia interschimb(a,b).
Observatii:
1. Utilizarea unei variabile temporare permite interschimbarea (corecta) a valorilor variabilelor.
2. Din aceast exemplu, retineti ca valoarea stocata la o adresa este cea rezultata dupa ultima operatie de atribuire sau de citire.
3. Aplicarea pasilor unui algoritm propus asupra unor date concrete permite detectarea eventualelor greseli de rationament. Aceasta, insa, nu este echivalenta cu testarea sau verificarea corectitudinii programului.
4. O utilizare comuna a acestei scheme intervine in interschimbarea valorilor a doua elemente de tablou (exemplu: a[i] si a[j]). Pasii pentru a realiza aceasta sunt: t:=a[i]; a[i]:=a[j]; a[j]:=t;
5. Fiind date doua variabile de tip intreg: x si y, interschimbarea valorile acestora se poate realiza fara a folosi o a treia variabila:
x:=x+y; y:=x-y; x:=x-y
6. O aplicare a interschimbarii apare in exemplul 1.6.
Exemplul 1.5. Se cere generarea primilor n termeni (n>1) ai sirului lui Fibonacci. Primii cativa termeni sunt: 0, 1, 1, 2, 3, 5, 8, 13, Mai precis, termenul curent este suma celor doi termeni anteriori
Vom prezenta doua metode. Prima metoda descrie schema de generare c := a + b, unde a, b desemneaza ultimii doi termeni generati, iar c va fi termenul curent. Deoarece se cer n termeni, este necesar un mecanism de numarare (incrementarea unei variabile de contorizare). Valorile contorului vor fi referite prin variabila k. Algoritmul de generare, in prima varianta, este:
Varianta 1:
1. citeste n
2. k := 2
3. a := 0; scrie a
4. b := 1; scrie b
5. repeta
i) c := a + b; scrie c
ii) a := b
iii) b := c
iv) k := k+1
pana cand k = n.
Prin a doua metoda se vor genera termenii doi cate doi. Aceasta inseamna ca uneori este generat unul in plus. Descrierea ce urmeaza foloseste numai variabilele a si b pentru a indica termenii sirului.
Varianta 2:
1. citeste n
2. a := 0
3. b :=1
4. k :=2
5. cat timp k < n executa
i) scrie a, b
ii) a := a + b
iii) b := a + b
iv) k := k+2
6. daca k = n atunci scrie a, b altfel scrie a.
|
Aplica algoritmul descris de varianta 2 pentru a genera primii 16 termeni ai sirului. Urmareste valorile variabilelor a si b. |
Exemplul 1.6. Se considera o secventa cu n numere intregi. Se cere afisarea numerelor in ordine crescatoare. Vom descrie sirul de numere prin x1, x2, , xn. Cea mai simpla metoda presupune interschimbarea a cate doua elemente, pana cand nu mai sunt necesare interschimbari. Pasii algoritmului sunt:
1. citeste n
2. citeste x1, x2, , xn
3. k:=1;
4. repeta
i) ordonat := true
ii) pentru i de la 1 pana la n-k executa
daca xi > xi+1 atunci
a) interschimb(xi, xi+1)
b) ordonat := false
iii) k:=k+1
pana cand (ordonat = true) or (k = n)
5. scrie x1, x2, , xn.
Justificarea metodei este simpla. Trebuie sa observam ca la prima parcurgere, elementul maxim va ajunge pe ultima pozitie. La a doua parcurgere, elementul imediat mai mic (decat maximul recent obtinut), va ocupa penultima pozitie. Cand nu sunt necesare interschimbari sirul este deja ordonat.
|
Cum functioneaza algoritmul, daca este aplicat asupra sirului: 4, 5, 9? Efectuati operatiile pas cu pas. |
1.2. Cum rezolvam probleme cu ajutorul calculatorului?
Am vazut ca exista probleme pentru care nu poate fi dat un algoritm de rezolvare. Totusi cele mai multe probleme cu care se confrunta informatica sunt probleme decidabile. Toate temele tratate in aceasta lucrare formuleaza probleme decidabile.
Se stie ca nu invatarea unui limbaj de programare este o sarcina dificila, ci rezolvarea algoritmica a problemelor decidabile. Este clar ca, inainte de a incepe scrierea unui program trebuie, mai intai, sa gasim (sau sa cunoastem deja) solutia algoritmica a problemei puse. Cum se gaseste solutia? Etapele descrise de G. Plya [6], pentru rezolvarea unei probleme de matematica, sunt valabile si in informatica.
Inainte de a incepe sa vedem cum se face, trebuie sa intelegem atat ipotezele problemei cat si ceea ce se cere. Deci, intelegerea problemei, ocupa primul loc in procesul cautarii unei metode de rezolvare a acesteia cu ajutorul calculatorului. Trebuie evidentiate datele de intrare si conditiile pe care acestea trebuie sa le indeplineasca. Este important sa identificam esentialul. De multe ori un enunt al unei probleme contine foarte multe elemente descriptive privind importanta problemei, consideratii de natura istorica, exemple, uneori chiar si etape distincte pentru obtinerea solutiei. Cerinta problemei furnizeaza, de multe ori, chiar idei privind modul de a ajunge la solutie. Considerarea unor configuratii particulare pentru datele de intrare si incercarea de a lucra asupra lor, pentru a gasi solutia, va contribui intotdeauna la o intelegere mai buna a enuntului.
Daca in enunt se sugereaza etapele rezolvarii, acestea implicand rezolvarea unor subprobleme, atunci trebuie sa aflam solutia algoritmica corespunzatoare fiecarei etape. Daca nu se specifica etape, dar putem descompune problema in subprobleme mai simple atunci solutia algoritmica a problemei initiale se va obtine prin 'compunerea' solutiilor subproblemelor. Deci este foarte important sa stim sa rezolvam probleme simple, eventual probleme reprezentative pentru anumite clase de probleme si sa stim sa descompunem (respectiv, sa reducem) problema initiala in (la) subprobleme usor de rezolvat si apoi sa construim solutia finala. Abordarea prin descompuneri repetate, cu detaliere pas cu pas se numeste abordare top-down sau rafinare iterativa. Abordarea prin care pornind de la solutii algoritmice ale unor probleme cunoscute, construim solutii ale altor probleme care au insa legatura cu problema de rezolvat, iar in final, urmand aceeasi modalitate construim solutia problemei a carei solutie se cere, se numeste abordare bottom-up. Aceasta metoda permite reutilizarea programelor existente si este tot mai importanta odata cu aparitia tehnicilor orientate obiect. De asemenea, pentru a obtine o solutie a unei probleme este util sa privim problema si comparativ cu alte probleme intalnite. Numai dupa investigarea acestor variante putem trece la stabilirea metodei de abordare.
Pentru probleme de complexitate ridicata, oricare din metodele de abordare top-down sau bottom-up, conduc la o solutie modulara, bazata pe subprograme sau, mai nou, la o solutie orientata obiect.
Multe din problemele de programare pot fi rezolvate usor daca solutia verifica anumite principii. Daca solutia problemei este o multime de elemente care se poate obtine pas cu pas, pornind de la multimea vida, prin adaugarea celui mai bun element neconsiderat inca (si ales conform anui anumit criteriu) spunem ca avem de-a face cu o abordare de tip greedy. Pentru probleme in care se cere o solutie optima care satisface principiul optimalitatii (principiul lui Bellman) se va aplica metoda programarii dinamice. Alte strategii pentru elaborarea algoritmilor sunt: metoda divide et impera, metoda backtracking, euristica etc.
1.3. Studiati si consolidati cunostintele
Numarare: Fiind date n numere intre 0 si 100 reprezentand punctajul obtinut de cei n elevi (studenti) la un concurs. Sa se determine numarul concurentilor care au obtinut cel putin 50 de puncte.
Cum se rezolva problema, manual, pentru urmatoarea situatie (n = 7)?
Raspuns: Parcurgi sirul si numeri valorile de la 50 in sus. Cum ai proceda pentru un sir cu 4000 de valori?
Descrierea algoritmului:
1. Cere utilizatorului numarul notelor ce urmeaza a fi analizate.
2. Initializeaza un contor cu valoarea 0 (zero).
3. Cat timp mai sunt note de prelucrat, repeta operatiile:
a) intreaba utilizatorul despre urmatoarea nota,
b) daca nota primita indeplineste conditia (adica este cel putin 50) atunci creste valoarea contorului cu 1.
4. Anunta utilizatorul asupra numarului notelor care indeplinesc conditia.
Aplicatii: Toate formele de numarare (vezi [2]).
Probleme suplimentare
. Determinati numarul numerelor de patru cifre divizibile cu un numar intreg dat (o varianta de rezolvare este furnizata de 1.2.5 [2]).
. Determinati numarul numerelor prime mai mici decat un numar natural dat.
. Determinati numarul elementelor unui sir de numere reale care apartin unui anumit interval [a, b] dat.
Suma numerelor: Fiind date n numere reale sa se calculeze si afiseze suma acestora. Presupunem ca n este un numar natural.
Obtinerea algoritmului:
1. (n >= 2) Deoarece putem aduna cate doua valori, putem organiza calculul astfel: s:=a_1+a_2; s:=s+a_3 ; pasul general -- i -- este s:=s+a_, iar in final s=s+a_n
2. (n >= 0) Initializam s cu zero (s:=0), pasul general se pastreaza:
-- i : s:=s+a_i
Concluzie: Nucleul algoritmului pentru sumarea a n numere necesita un pas special urmat de n iteratii:
1. Calculeaza suma initiala (s = 0) ca un caz special (Zero este element neutru la adunare).
2. Formeaza fiecare din cele n sume partiale din valoarea anterioara printr-un proces iterativ.
3. Afiseaza suma celor n numere.
Descrierea algoritmului:
1. Intreaba utilizatorul si citeste numarul numerelor de adunat.
2. Initializeaza suma a zero numere.
3. Cat timp au fost procesate mai putin de n numere, executa:
(a) citeste urmatorul numar,
(b) calculeaza suma curenta prin adunarea numarului recent citit la suma numerelor anterior citite.
4. Afiseaza suma celor n numere.
Observatii:
1. Sunt necesare n-1 adunari. Implementarea foloseste n din motive de simplitate a descrierii. Ce modificare se face pentru a calcula produsul?
2. Metoda utilizata nu ia in considerare eventualele erori de calcul in privinta preciziei operatiilor (vezi 1.2.13 [2]).
Aplicatii: Calcularea mediilor aritmetica si armonica, alte calcule statistice etc. Ilustram prin urmatoarele exemple:
Fie X un sir cu N numere reale strict pozitive. Sa se calculeze si sa se afiseze: media aritmetica, media geometrica si media armonica.
Pentru a parcurge, mai usor, textul programului Pascal ce urmeaza, reamintim formulele necesare. Daca X1, X2, , XN sunt numerele din enunt, M_aritm este media aritmetica, M_geom este media geometrica, iar M_armon reprezinta media armonica, atunci:
M_aritm = ![]() M_geom =
M_geom = ![]()
si
M_armon = 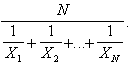
Pentru calculul radicalului (puterilor) vezi si problemele 1.2.4, 1.2.6 si 1.2.15. [2]
Probleme suplimentare:
. Calculul sumei S = a1a2 + a3a4 + . +a2k-1a2k, unde k se citeste de la tastatura, iar an este termenul general al unui sir de numere.
. Calculul sumei patratelor elementelor unui tablou unidimensional.
. Calculul termenului general al unui sir dat print-o suma (vezi tema: 1.2.7) [2].
Cautare intr-un sir ordonat: Cautarea unui obiect intr-o structura de date de tip tablou poate fi realizata prin investigarea elementelor de la inceput spre sfarsit sau de la sfarsit spre inceput folosind algoritmul ilustrat in problema 1.2.2. [2]. Daca elementele tabloului sunt (sau pot fi) ordonate crescator (dupa o anumita componenta a informatiei - numita cheie) atunci cautarea poate fi realizata mai eficient.
Fiind dat un tablou unidimensional X cu N elemente si o valoare y, se cere sa se precizeze daca y apare sau nu printre elementele tabloului X.
Descrierea algoritmului:
Regulile algoritmului de cautare (numit in continuare cautare binara) pot fi imediat descrise daca notam prin linf - limita inferioara a portiunii din tablou in care se face cautarea si, prin lsup - limita superioara a acestei zone.
Cautarea se va face in zona: X linf+1 , X linf+2 , ., X lsup-2 , X lsup-1 : Initial linf = 0; lsup = N + 1; Se repeta urmatoarea secventa de operatii:
se determina M - pozitia de mijloc a intervalului (linf, lsup);
se compara y cu X M : daca y < X M atunci cautarea va continua intre linf si lsup = M; daca y = X M atunci a fost gasita valoarea y si are loc oprirea iteratiei; daca y > X M atunci urmatoarea cautare se va face intre M si lsup, deci pentru linf = M.
Daca la un moment dat se obtine lsup = linf +1 si nu a fost gasita valoarea y inseamna ca aceasta nu exista in sir si programul se incheie.
|
Scrieti algoritmul dupa modelul de mai sus. Numarati cate comparatii sunt necesare atunci cand elementul de cautat nu s-ar afla in sir. |
Bibliografie
G. Albeanu, Algoritmi si limbaje de programare, Editura FRM, Bucuresti, 2000.
G. Albeanu, Luminita Radu, Algoritmica si programare in limbajul Pascal, Editura FRM, Bucuresti, 2001.
C. Calude, Complexitatea calculului. Aspecte calitative. Editura Stiintifica si Enciclopedica, Bucuresti, 1982.
D. Knuth, Arta programarii calculatoarelor. Volumul I: Algoritmi fundamentali, Teora, Bucuresti, 1999.
P. S. Novikov, Elemente de logica matematica, Editura Stiintifica, Bucuresti, 1966.
G. Plya, Cum rezolvam o problema?, Editura Stiintifica, Bucuresti, 1965.
Cuv|ntul algoritm, initial, desemna orice proces de calcul realizat pe baza unor reguli in care interveneau numere scrise zecimal. Acest cuv|nt provine din pronuntia fonetica a numelui unui mare matematician arab: Abu Abdulah Muhamed ibu Musa al-Horezmi (780-850) care in lucrarile sale de aritmetica si algebra a indicat reguli precise pentru operatiile aritmetice fundamentale.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3036
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved